Similar presentations:
Решение задач на применение первого признака равенства треугольников
1.
Решение задач на применениепервого признака равенства
треугольников
2.
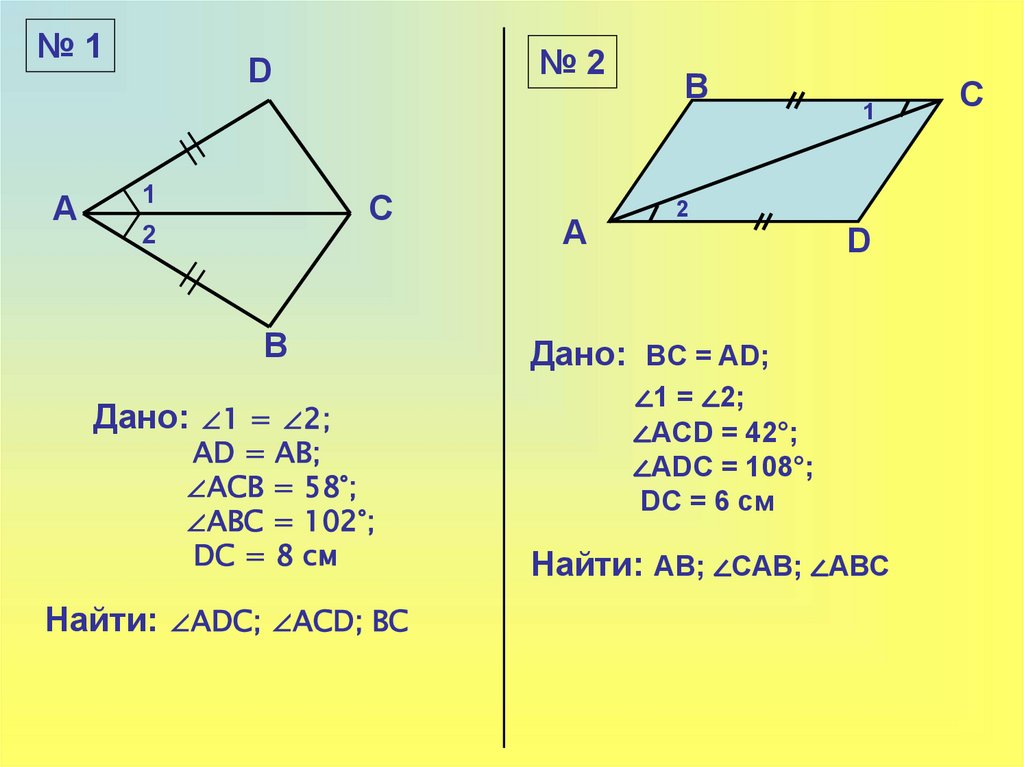
№1А
№2
D
1
С
2
В
Дано: ∠1 = ∠2;
AD = AB;
∠ACB = 58°;
∠ABC = 102°;
DC = 8 см
Найти: ∠ADC; ∠ACD; BC
А
В
1
2
D
Дано: BC = AD;
∠1 = ∠2;
∠ACD = 42°;
∠ADC = 108°;
DC = 6 см
Найти: АВ; ∠САВ; ∠АВС
С
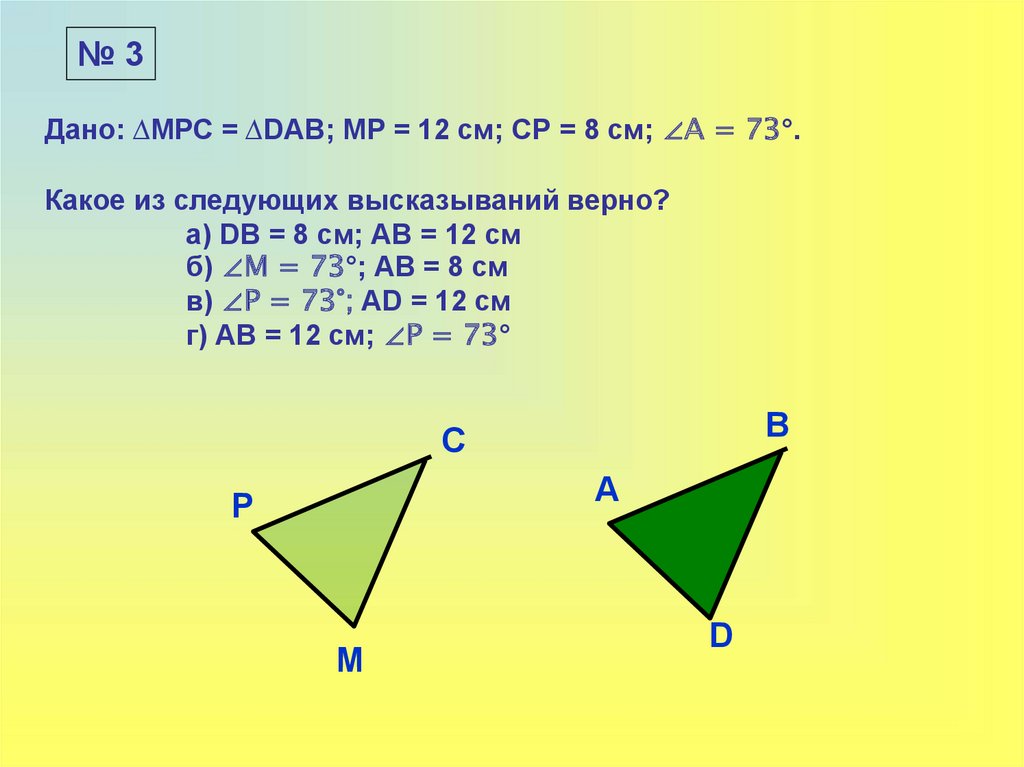
3.
№3Дано: ∆МРС = ∆DAB; МР = 12 см; СР = 8 см; ∠А = 73°.
Какое из следующих высказываний верно?
а) DB = 8 см; АВ = 12 см
б) ∠М = 73°; АВ = 8 см
в) ∠Р = 73°; АD = 12 см
г) АВ = 12 см; ∠Р = 73°
B
C
A
P
M
D
4.
Назовите углы:• ∆DEK, прилежащие к стороне ЕК;
• ∆MNP, прилежащие к стороне MN.
Назовите угол:
• ∆DEK, заключённый между сторонами DЕ и DК;
• ∆MNP, заключённый между сторонами NР и РМ.
Между какими сторонами:
• ∆DEK заключён угол К;
• ∆MNP заключён угол N?
∆АВС = ∆SPK. Назовите равные
стороны и равные углы в этих
треугольниках.
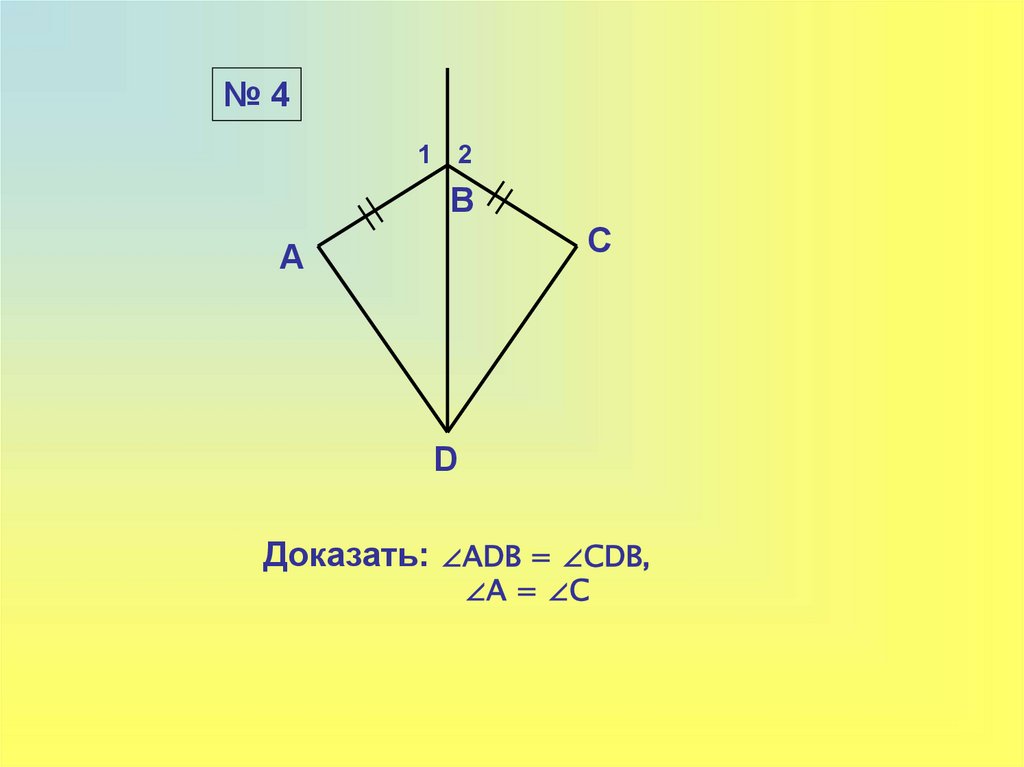
5.
№41
2
В
С
А
D
Доказать: ∠ADB = ∠CDB,
∠A = ∠C
6.
Дано: ∠AВЕ = ∠ЕCD,E
№5
ВЕ = СЕ; ВК = LC,
∠ВКЕ = 110°
Доказать: ∆ВКЕ = ∆CLE
Найти: ∠ ELC
D
А
В
K
L
С
Доказательство:
∠АВЕ и ∠КВЕ – смежные, ∠АВЕ + ∠КВЕ = 180° ⇒ ∠КВЕ = 180° - ∠АВЕ.
∠DCE и ∠LCЕ – смежные, ∠DCE + LCЕ =180° ⇒ ∠LCЕ = 180° - ∠DCE.
По условию задачи ∠AВЕ = ∠ЕCD.
По доказанному ∠КВЕ = 180° - ∠АВЕ и ∠LCЕ = 180° - ∠DCE ⇒ ∠КВЕ = ∠LCЕ.
В ∆ВКЕ = ∆ELC: 1) ВК = LC (по условию задачи)
2) ВЕ = СЕ (по условию задачи)
3) ∠КВЕ = ∠LCЕ (по доказанному)
Решение:
Так как ∆ВКЕ = ∆СLЕ по доказанному, то ∠ELC =
Ответ: ∠ ELC = 110°.
⇒ ∆ВКЕ = ∆CLE (по двум
сторонам и углу между
ними)
∠BKE = 110°.
7.
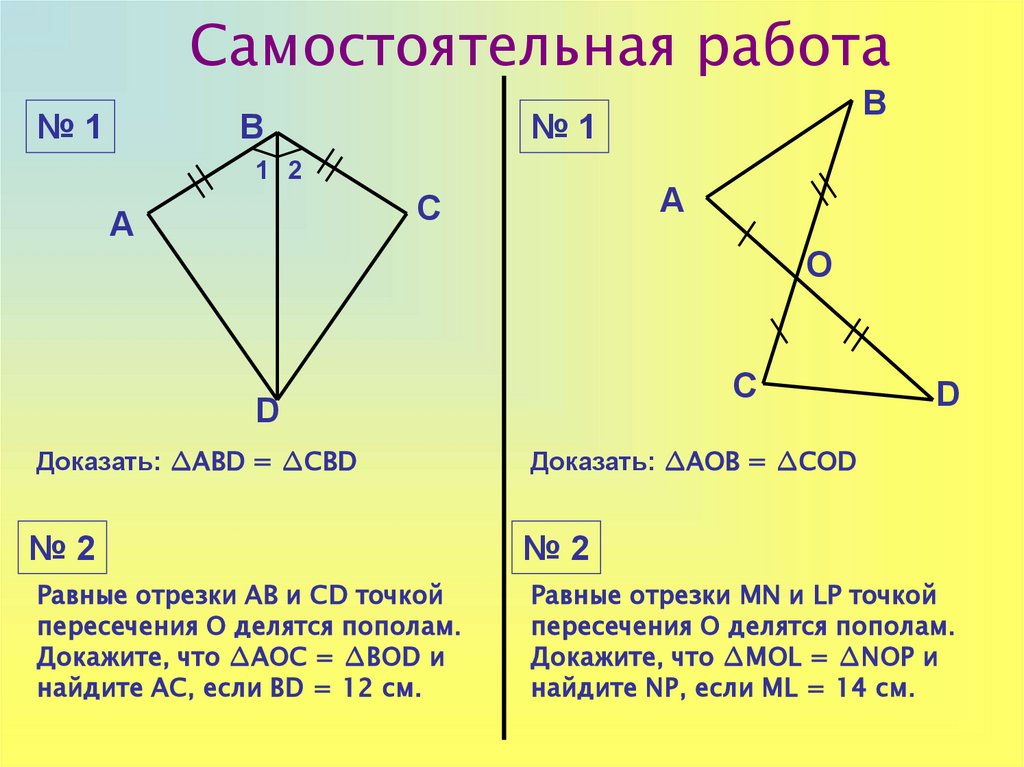
Самостоятельная работа№1
В
№1
1 2
А
С
А
В
О
С
D
Доказать: ∆AВD = ∆CВD
№2
Равные отрезки АВ и СD точкой
пересечения О делятся пополам.
Докажите, что ∆АОС = ∆ВОD и
найдите АС, если ВD = 12 см.
D
Доказать: ∆AОВ = ∆CОD
№2
Равные отрезки MN и LP точкой
пересечения О делятся пополам.
Докажите, что ∆MОL = ∆NОP и
найдите NP, если ML = 14 см.
8.
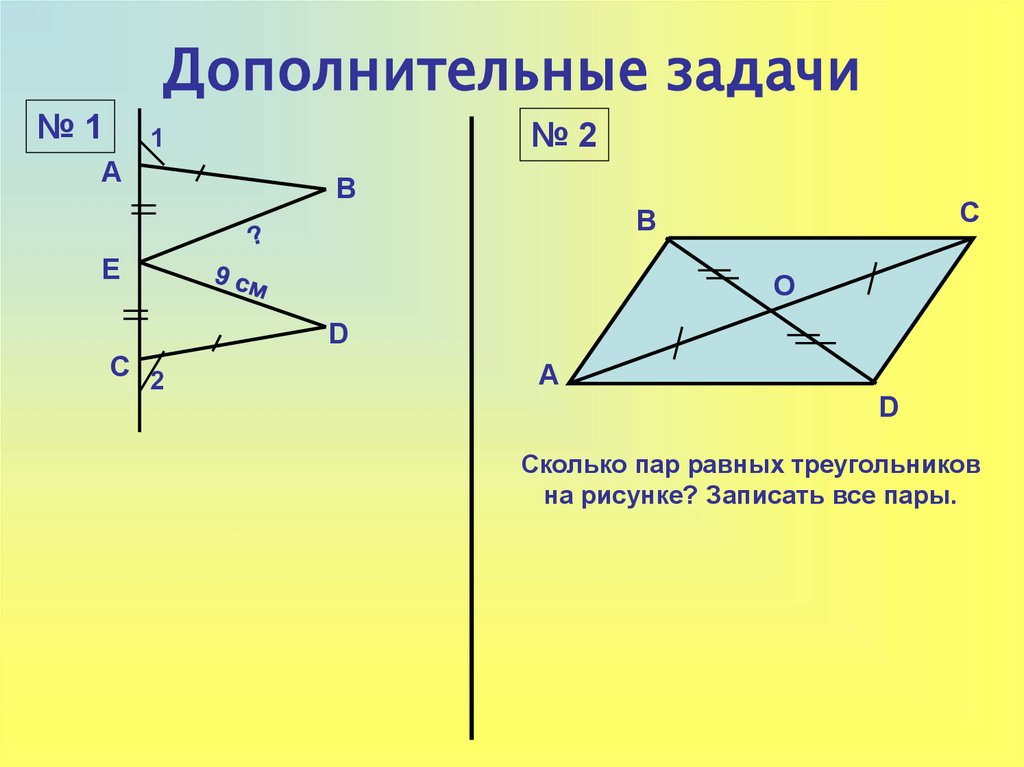
Дополнительные задачи№1
№2
1
А
В
С
В
Е
О
D
С 2
А
D
Сколько пар равных треугольников
на рисунке? Записать все пары.
9.
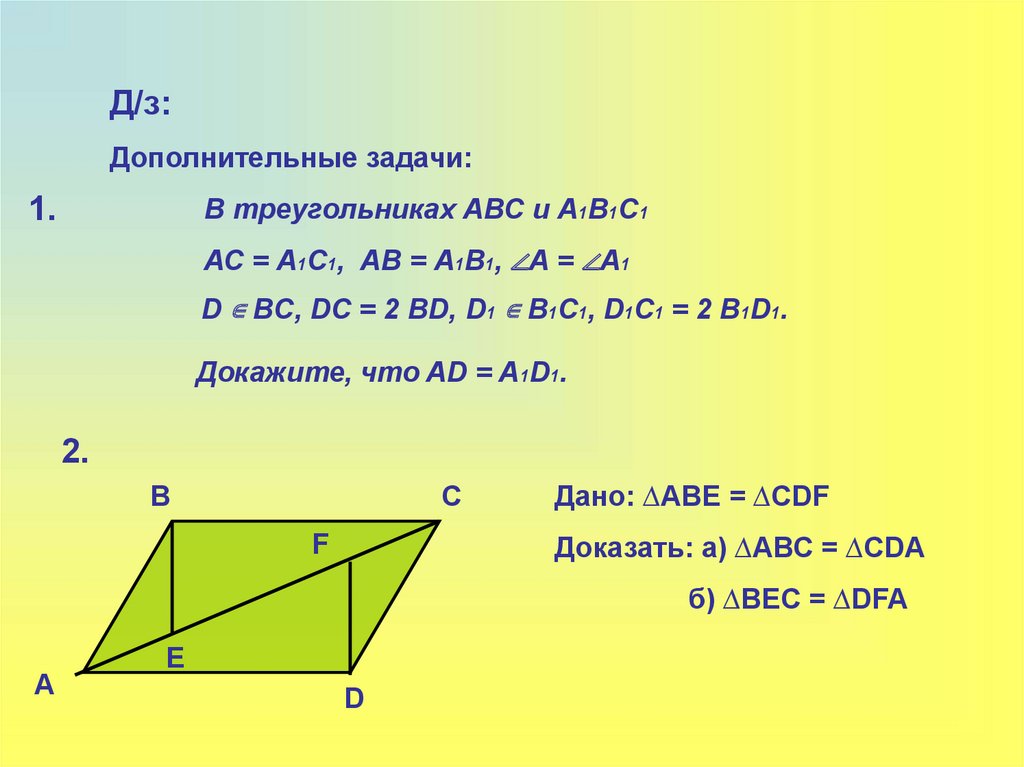
Д/з:Дополнительные задачи:
В треугольниках АВС и А1В1С1
1.
АС = А1С1, АВ = А1В1, ∠А = ∠А1
D ∊ BC, DC = 2 BD, D1 ∊ B1C1, D1C1 = 2 B1D1.
Докажите, что AD = A1D1.
2.
В
С
Дано: ∆АВЕ = ∆CDF
Доказать: а) ∆АВС = ∆CDA
F
б) ∆ВЕС = ∆DFA
А
Е
D



 mathematics
mathematics








