Similar presentations:
Статистика и теория вероятностей (9 класс)
1. СТАТИСТИКА И ТЕОРИЯ ВЕРОЯТНОСТЕЙ 9 класс
Испытания Бернулли2. Цели урока:
знать, что такое отдельное испытаниеБернулли, что такое успех и неудача и как
связаны их вероятности;
понимать, что такое серия независимых
одинаковых испытаний Бернулли. Здесь
независимость понимается в обычном
смысле – как отсутствие влияний одного
испытания на другое;
уметь вычислять вероятность
элементарного события вида НУНУ в серии
из n испытаний Бернулли;
уметь вычислять число элементарных
событий, благоприятствующих ровно к
успехам в серии испытаний Бернулли;
знать формулу вероятности ровно к
успехов и уметь ею пользоваться.
3. Повторение ТЕОРИИ
Случайное событие - событие называется случайным,если нельзя утверждать, что это событие в данных
обстоятельствах произойдет.
Элементарное событие –
Вероятность –
Частота случайного события –
Маловероятное случайное событие –
Равновероятные события –
Достоверное событие –
Невозможное событие –
Наибольшее и наименьшее значение вероятности –
Несовместные события –
Независимые события –
4. Испытание Бернулли
Определение:Испытанием
Бернулли называют
случайный опыт,
который может
закончиться одним
из двух
элементарных
событий.
5. УСПЕХ И НЕУДАЧА
Одно из двухэлементарных событий
в таких опытах условно
называют успехом, а
другой — неудачей.
Вероятность того, что
опыт закончится
успехом, обычно
обозначают буквой р.
Вероятность неудачи
обозначают q. Числа р
и q положительные,
при этом
p + q= 1.
6. Серия или последовательность испытаний Бернулли
Если проводитсянесколько одинаковых
и независимых
испытаний Бернулли
подряд, то говорят, что
проведена серия или
последовательность
испытаний Бернулли.
Серия испытаний
Бернулли также
является случайным
экспериментом.
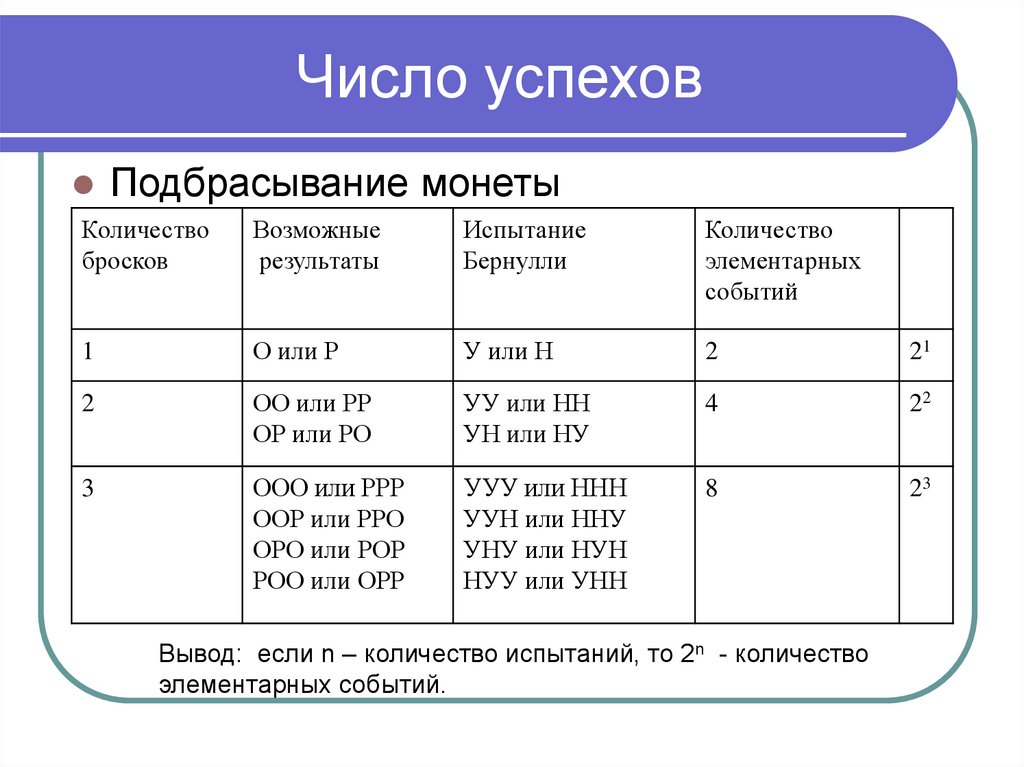
7. Число успехов
Подбрасывание монетыКоличество
бросков
Возможные
результаты
Испытание
Бернулли
Количество
элементарных
событий
1
О или Р
У или Н
2
21
2
ОО или РР
ОР или РО
УУ или НН
УН или НУ
4
22
3
ООО или РРР
ООР или РРО
ОРО или РОР
РОО или ОРР
УУУ или ННН
УУН или ННУ
УНУ или НУН
НУУ или УНН
8
23
Вывод: если n – количество испытаний, то 2n - количество
элементарных событий.
8. Вероятность успеха
При одном подбрасываниимонеты вероятность
выпадения орла (О или Р - У
или Н)
1
p q
2
При двух подбрасываниях
монеты вероятность
события -выпадение орла
при каждом броске (ОО, то
есть УУ)
1 1
p2
2 4
2
9. Вероятности событий
При проведении серии из nнезависимых испытаний
Бернулли одно элементарное
событие с k успехами имеет
вероятность
Число таких элементарных
событий с k успехами равно
событие «наступило ровно к
успехов» имеет вероятность
k
n
k
C p q
n k
k
p q
C
n k
k
n
10. Пример 1.
Выполним расчеты по формуле вероятностейk
n
k
C p q
n k
, где
11. Решение.
n!P ( A)
p k q n k
k! n k !
3
7!
1 2
P( A)
3! 7 3 ! 3 3
4
7 6 5 1 2 4
560
P( A)
0,256
3
4
3 2 1 3 3
2187
12. Пример 2.
Иван Иванович купил билет«Спортлото 5 из 36». Он должен
зачеркнуть ровно 5 номеров из 36.
Сколько существует способов это
сделать?
Найдите вероятность угадать 5
номеров из 36.
13. Число успехов
5С36
36!
5! 36 5 !
5
C36
376992
376992 способа зачеркнуть ровно 5 номеров из 36
Значит, вероятность угадать ровно 5 номеров из
36 равна
P ( A)
1
C nk
P ( A)
1
0,000003
376992
14. Пример 3.
Проводится серия из 3 независимыхиспытаний Бернулли с вероятностью
успеха p 1
Найдите вероятность
6
элементарного события, в котором
наступает сначала 1 успех, а затем — 2
неудачи.
15. Решение.
Проводится серия из 3 независимых испытаний Бернулли с1
вероятностью успеха
Найдите вероятность
6
элементарного события, в котором наступает сначала 1
успех, а затем — 2 неудачи.
Решение.
n=3, k=1, p= 1 , q=1- 1 = 5
6
6
6
Выполним расчеты по формуле
вероятностей
Cnk p k q n k , где
2
3! 1 5
25
P( A)
0,347
1! 2! 6 6
72
16. Самостоятельная работа №2
Вариант 11. Проводится серия из 6
независимых испытаний
Бернулли с 1вероятностью
успеха р = 3 .Найдите
вероятность элементарного
события, в котором
наступает сначала 2 успеха,
а затем — 4 неудачи.
2. Сколько элементарных
событий с 4 успехами
возможно в серии из 10
испытаний Бернулли?
3. Найдите вероятность
выбросить ровно 6 орлов,
10 раз бросив монету.
Вариант 2
1. Проводится серия из 6
независимых испытаний
Бернулли с1вероятностью
успеха р = 2 . Найдите
вероятность элементарного
события, в котором
наступает сначала 4 успеха,
а затем — 2 неудачи.
2. Сколько элементарных
событий с 6 успехами
возможно в серии из 10
испытаний Бернулли?
3. Найдите вероятность
выбросить ровно 4 орла, 10
раз бросив монету.
17. Вероятность событий
n!k
n k
P ( A)
p q
k! n k !
где
n- количество испытаний
k- количество успехов
p- вероятность успеха
q- вероятность неудачи
18.
Фотоматериал использован из свободного доступасети Интернет для наглядного представления
теоретических фактов.

















 mathematics
mathematics