Модель перевода чисел из одной системы счисления в другую (лекция № 7)

1.

2.5 Модель перевода чисел из
одной системы счисления в
другую

2.

Перевод целых чисел из десятичной системы счисления в другую.
Алгоритм
перевода
можно
записать
в
виде
следующей
последовательности шагов:
1. Разделить в целых числах заданное число А на основание р той
системы в которую переводят, и запомнить частное q и остаток а.
2. Если частное не равно нулю, то принять его за новое число и
вернуться к шагу 1.
3. Если частное равно нулю, действия прекратить. Выписать остатки в
порядке, обратном их получению, и принять их за цифры искомого числа
аnan-1…a1a0. Арифметические действия по данному алгоритму производят в
той системе счисления, из которой число переводят.

3.

Примеры.
1. Перевести число 25(10) в двоичную систему счисления:
25
-24
1
2
12
-12
0
2
6
-6
0
Итак, 25(10)=11001(2).
2
3
-2
1
2
1

4.

Для перевода чисел из любой позиционной системы счисления в
десятичную можно воспользоваться выражением:
аnpn + аn-1pn-1 + аn-2pn-2 + … + а2p2 + а1p1+ а0p0
Сначала в десятичную СС переводится основание той системы, из
которой осуществляется перевод, а затем цифры исходного числа аk.
Результаты подставляются в выражение.
Полученная сумма дает искомый результат. Этот способ называется
алгоритмом замещения.
Пример. Перевести в десятичную СС числа C7(16) и 1010(2):
1. С7(16)=12.161 +7.16°=192 + 7 = 199(l0);
2. 1010(2) =1.23 +1.21=8 + 2=10(10).

5.

2. Перевести число 83(10) в двоичную систему счисления, а полученный
результат в десятичную по алгоритму замещения.
83
2
-82
41
2
1 -40
20
2
1 -20
10
2
0 -10
5
2
0
-4
2
2
1
-2
1
0
Итак, 83 =1010011 .
(10)
(2)
Проверка:
1010011(2)= 1.26 +0.25 +1.24 +0.23 +0.22 +1.21 +1.2°=64+16+2+1=83(10).

6.

В некоторых частных случаях для перевода из одной системы
счисления в другую можно воспользоваться выражениями:
2 1000
...000
m
m
2m 1 1111
...
111
m
Методика упрощенного перевода ясна из следующих примеров.
Примеры. Перевести в двоичную систему счисления приведенные ниже
десятичные числа, пользуясь упрощенным способом:
а) 65(10) = 64 + 1 = 26 + 1 = 1000000(2) + 1(2) =1000001(2);
б) 1030(10)= 1024 + 6 = 2010 + 6 = 10000000000(2)+110(2) =10000000110(2).
в) 31(10) = 32 -1 = 25 - 1 = 100000(2) - 1(2) =11111(2).

7.

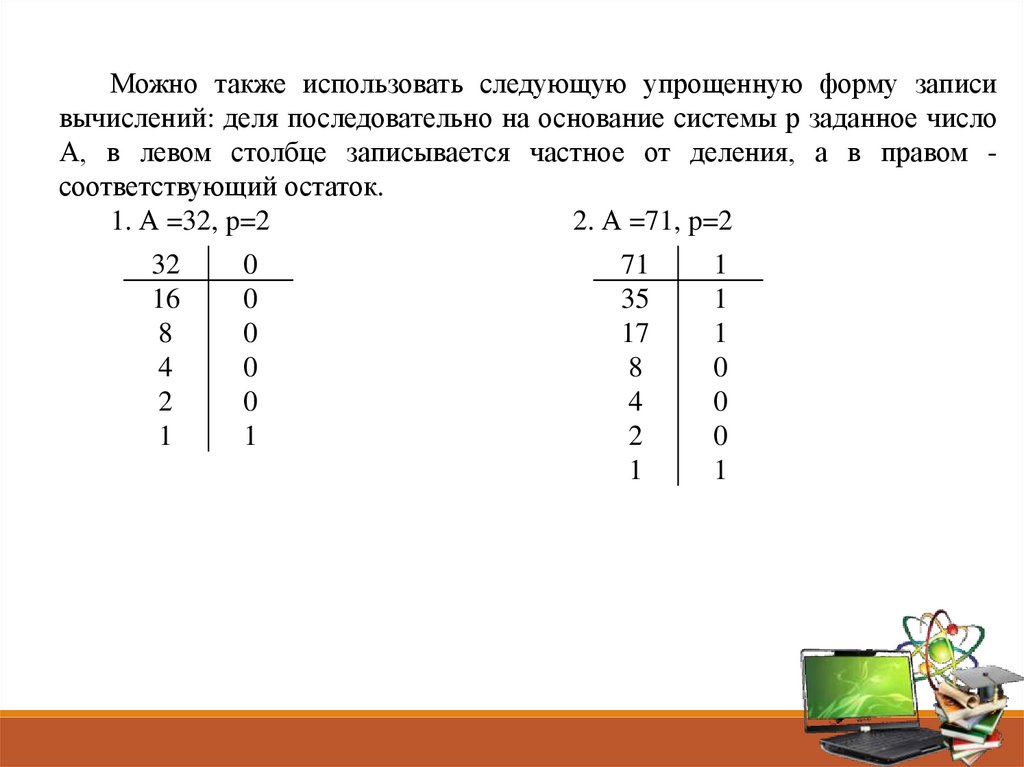
Можно также использовать следующую упрощенную форму записи
вычислений: деля последовательно на основание системы р заданное число
А, в левом столбце записывается частное от деления, а в правом соответствующий остаток.
1. А =32, p=2
2. А =71, p=2
32
16
8
4
2
1
0
0
0
0
0
1
71
35
17
8
4
2
1
1
1
1
0
0
0
1

8.

Перевод десятичных дробей в другую систему счисления.
Дробь в новой системе счисления может быть как конечной, так и
бесконечной. Процесс прекращается при получении достаточной точности.
Алгоритм перевода десятичных дробей в другую систему счисления
можно описать в виде следующей последовательности шагов:
1. умножить исходную дробь на основание р, той системы счисления в
которую дробь переводится. Все вычисления производятся в исходной
(десятичной) системе счисления;
2. выделить из полученного результата целую часть и принять ее за
цифру очередного разряда искомой дроби;
3. если достигнута необходимая точность, то дальнейшие действия
прекратить. В противном случае из последнего результата умножения
выделить дробную часть, принять ее за исходное число и перейти к шагу 1.
Искомая дробь в новой системе запишется в виде последовательности
целых частей полученных произведений, начиная с первого.

9.

Примеры.
1. Перевести в двоичную СС дробь 0,3125(10):
0, 3125
0
6250
1
2500
0
5000
1
0000
0,3125(10)=0,0101(2)
2. Перевести в двоичную СС дробь 0,12(10):
0,
12
0
24
0
48
0
96
1
92
1
84
1
68
1
36
0,12(10)=0,0001111(2)

10.

Перевод правильных дробей в десятичную СС можно выполнить с
помощью описанного ранее алгоритма замещения.
Примеры.
1. Перевести в десятичную СС число 0,1101(2):
1
1
1
0,1101(2) 1 2 4 0,5 0,25 0,0625 0,8125 (10)
2
2
2
2. Перевести в десятичную СС число 0,71(16):
7
1
113
0,71(16) 1 2
0,4414(10)
16 16
256