Квантовый эффект Холла

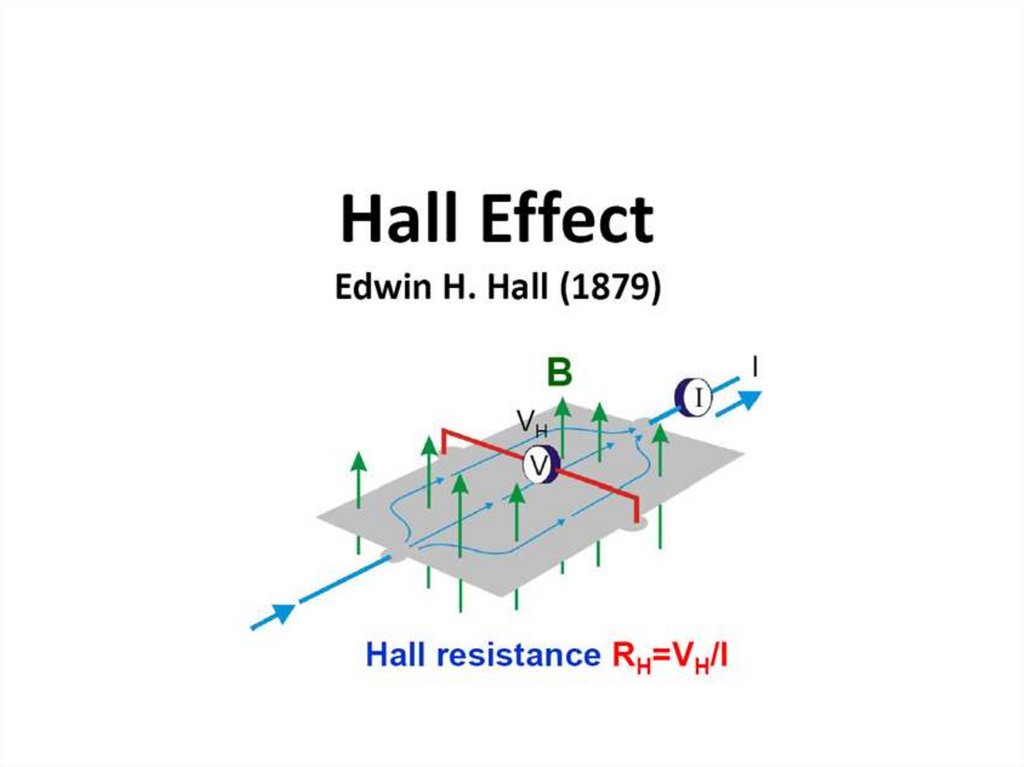
1. Квантовый эффект Холла

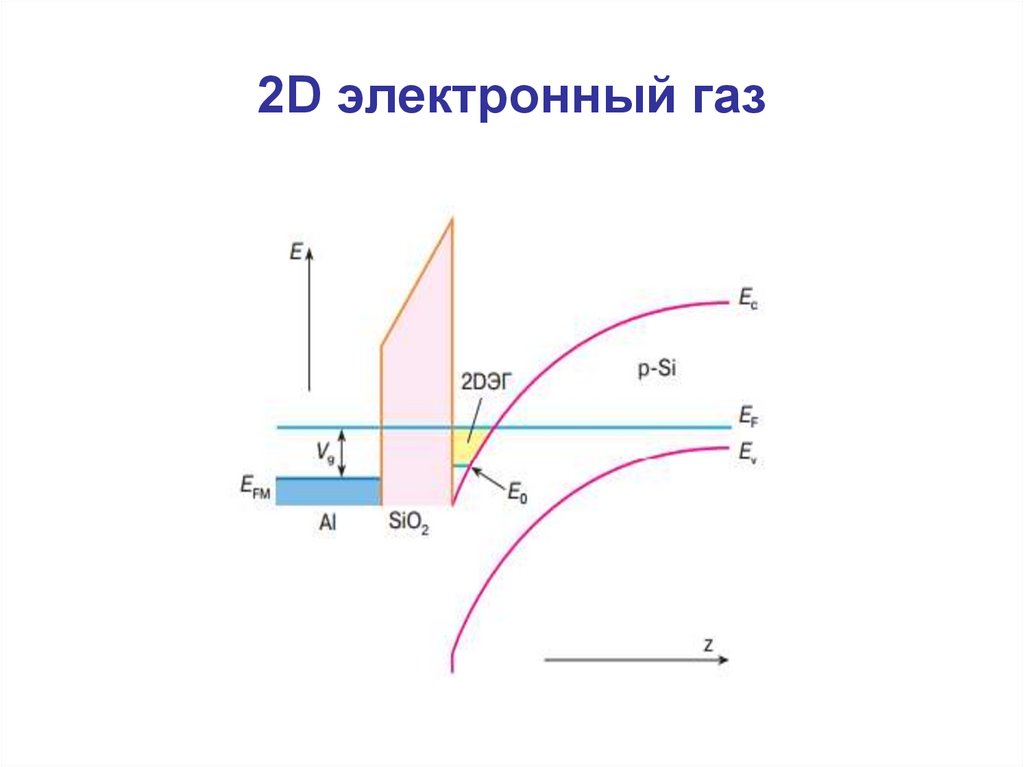
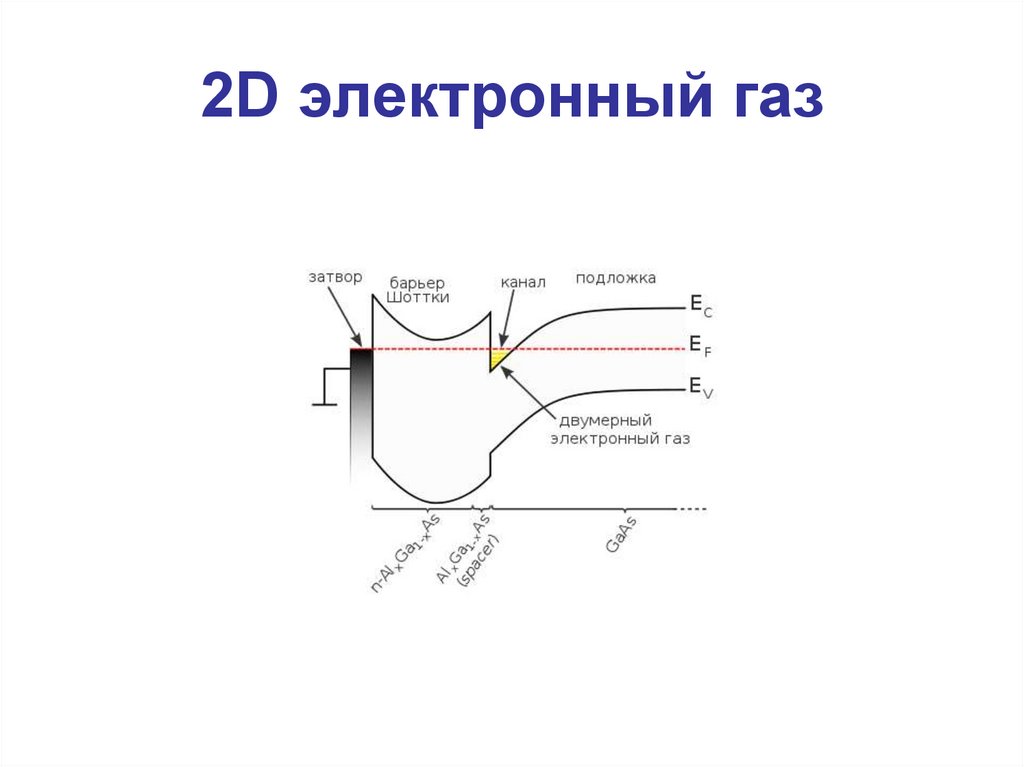
2. 2D электронный газ

3. 2D электронный газ

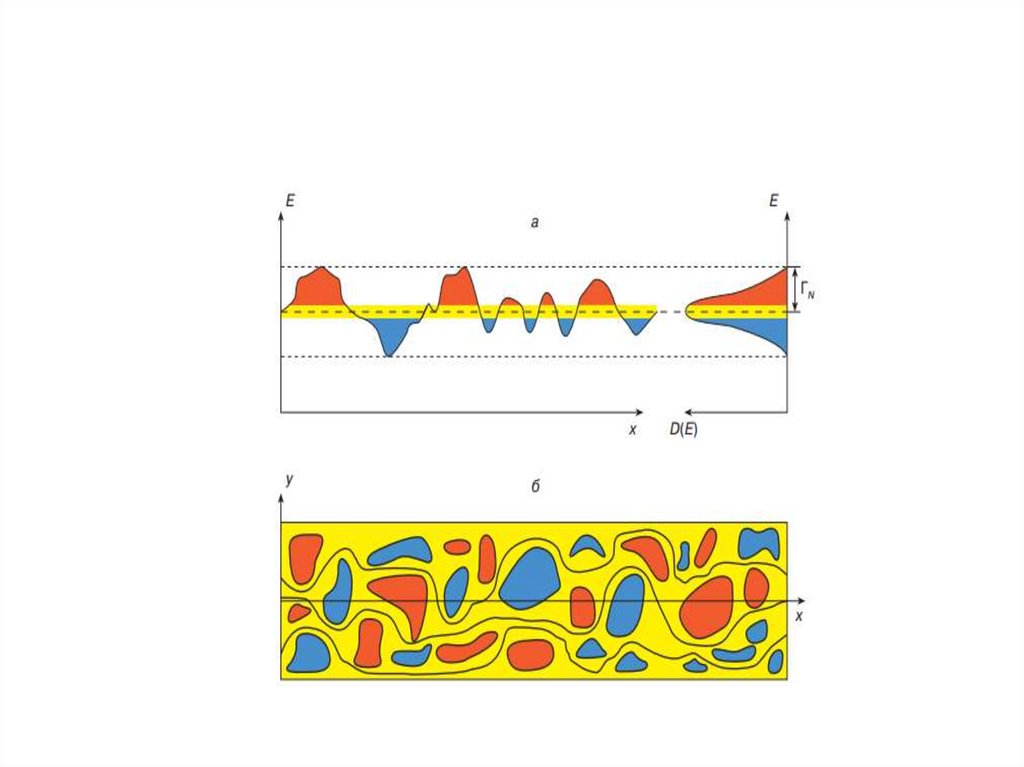
4.

5.

6.

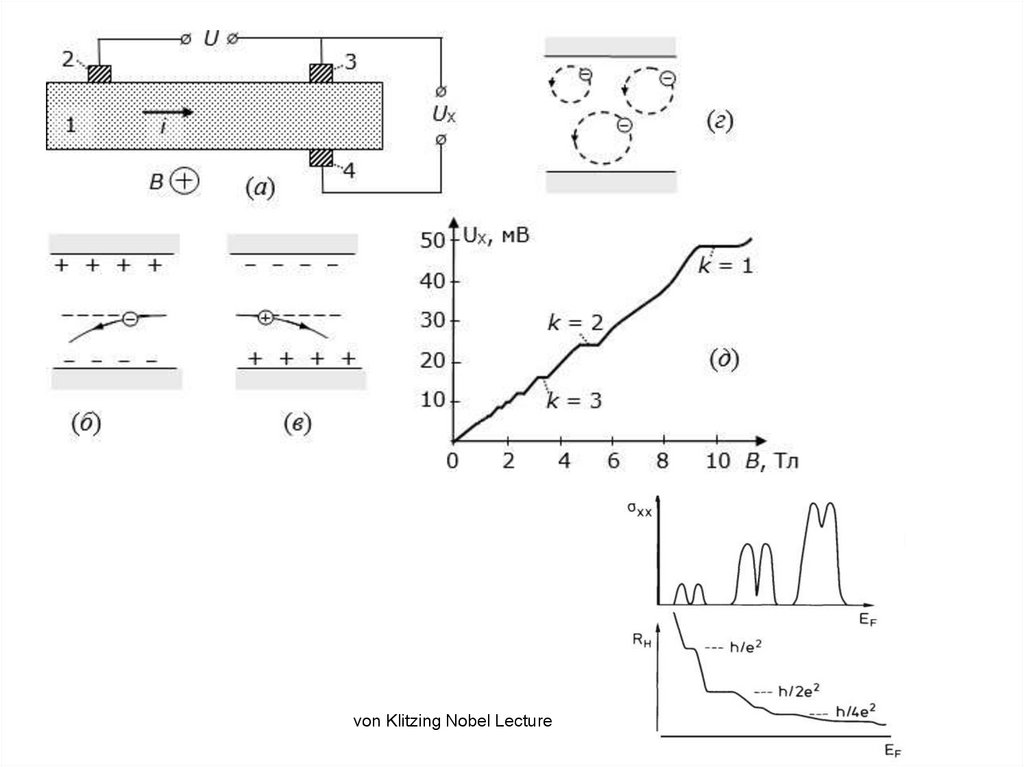
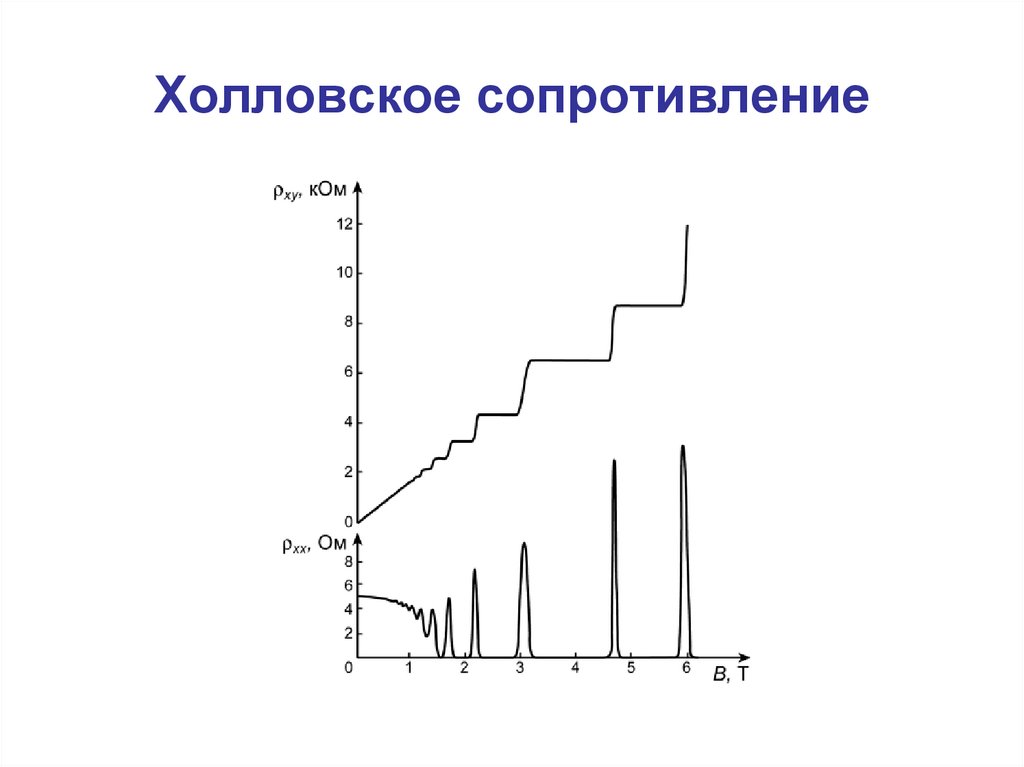
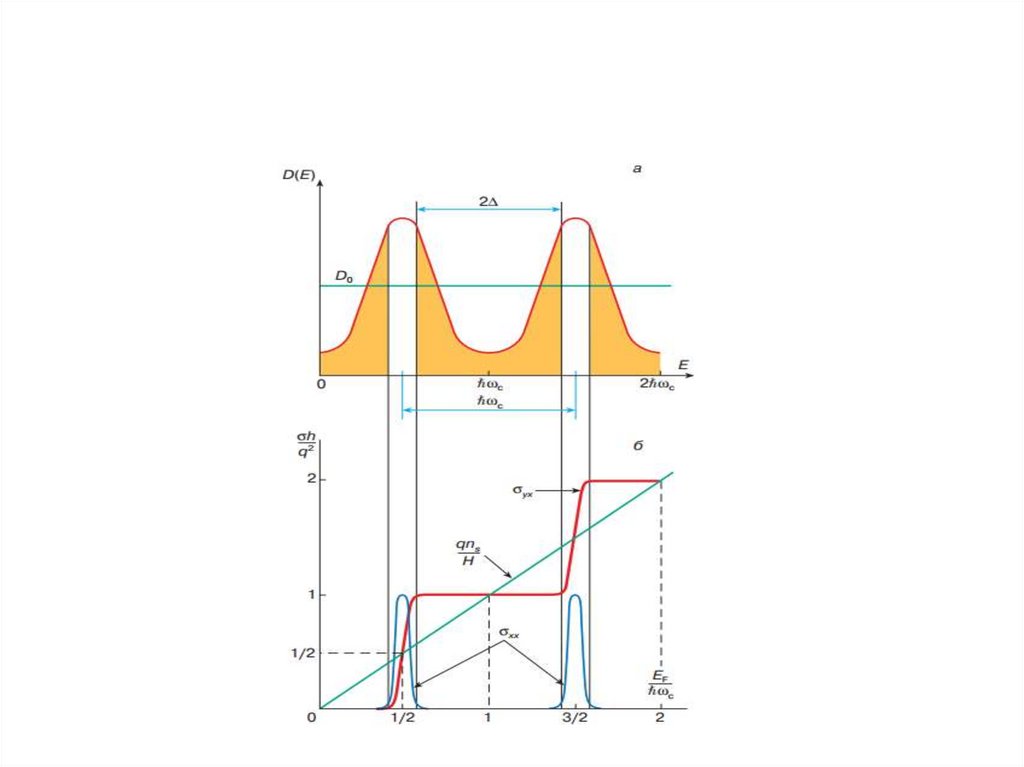
von Klitzing Nobel Lecture

7. Холловское сопротивление

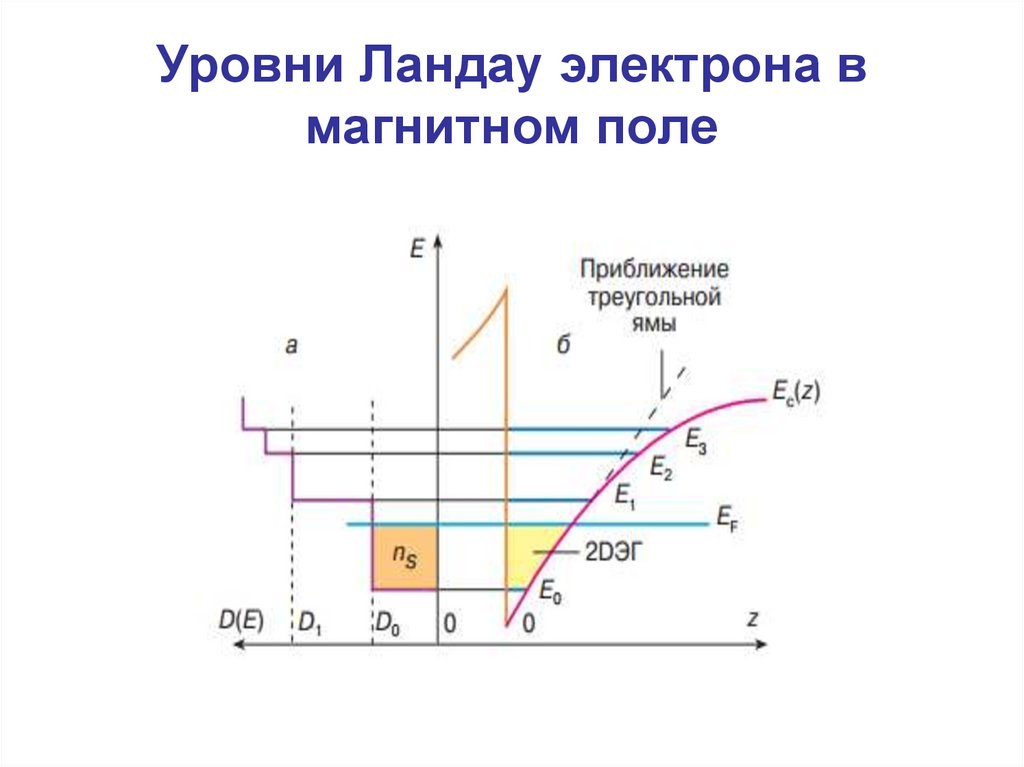
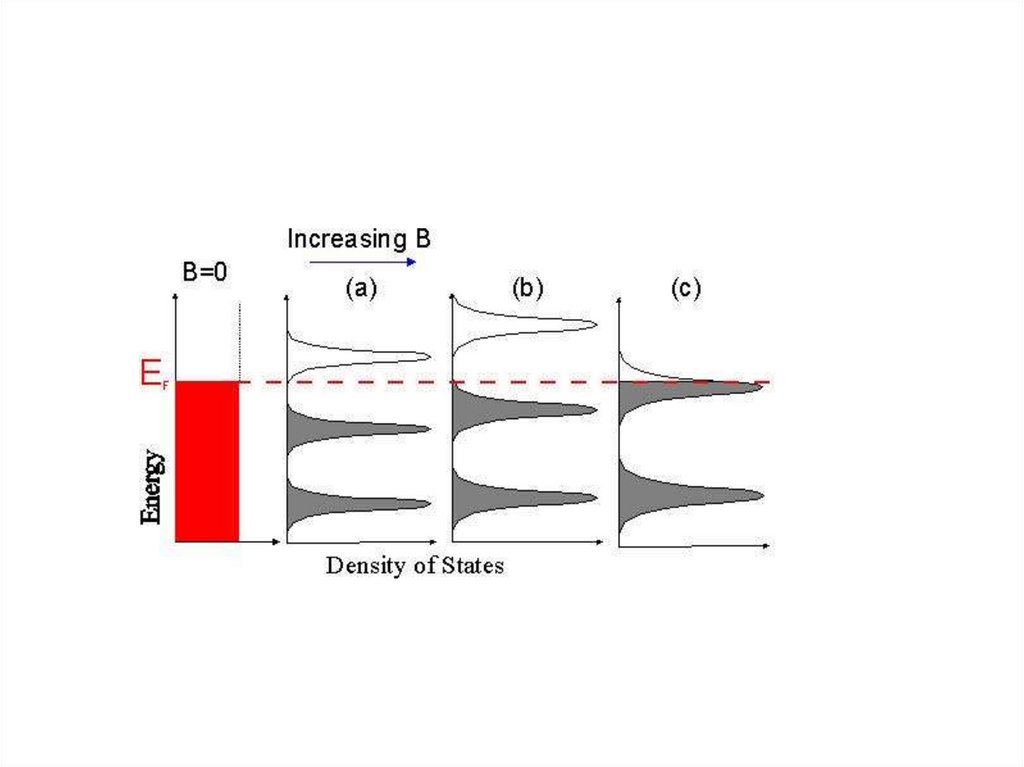
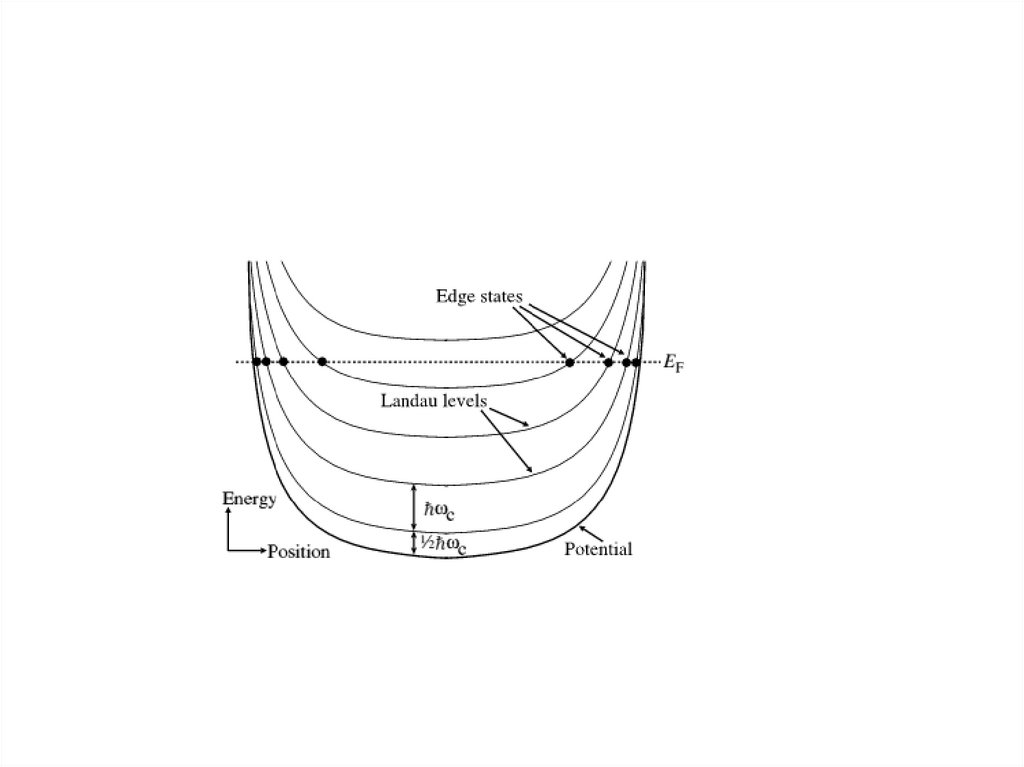
8. Уровни Ландау электрона в магнитном поле

9.

10.

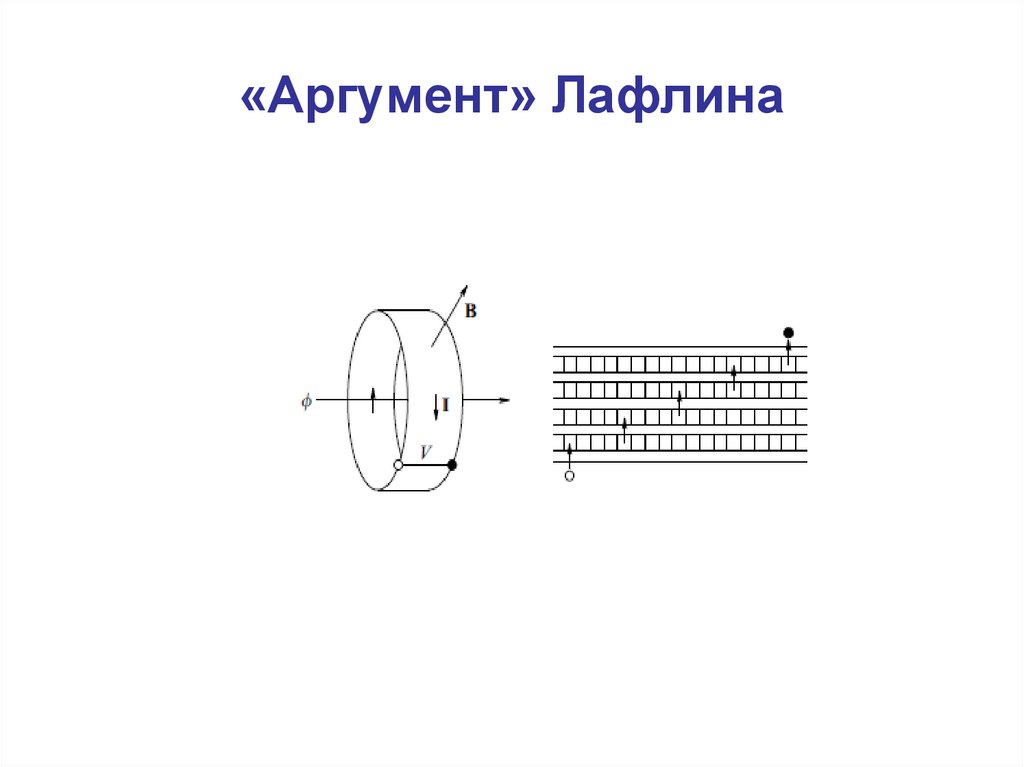
11. «Аргумент» Лафлина

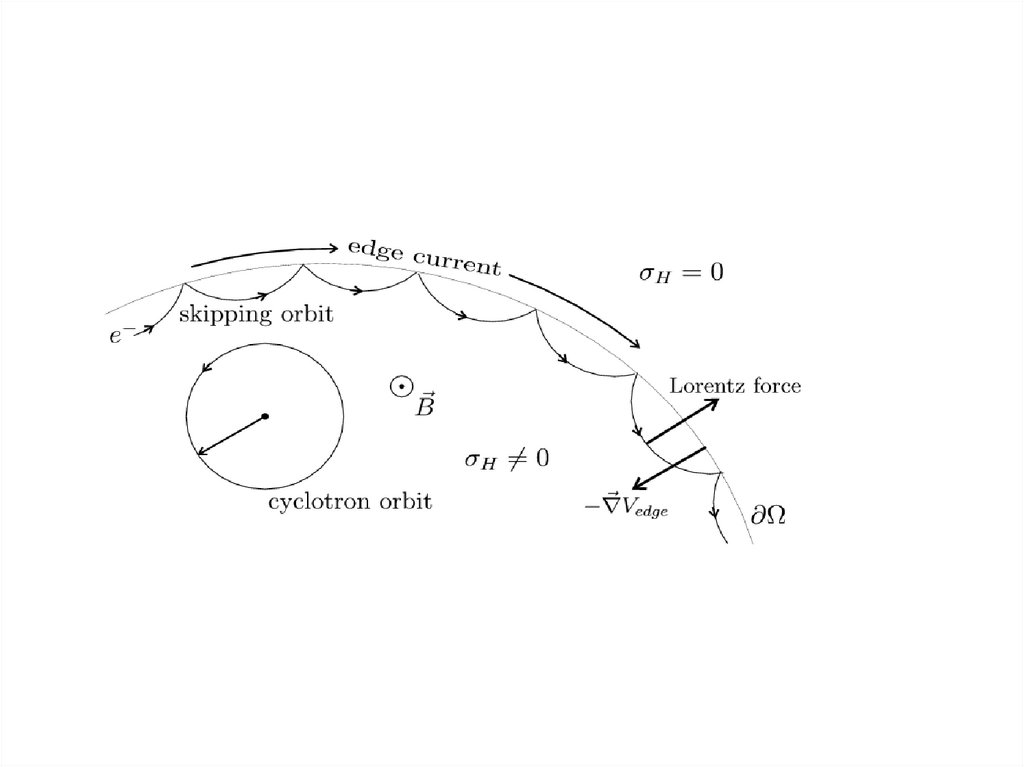
12.

13.

14.

15.

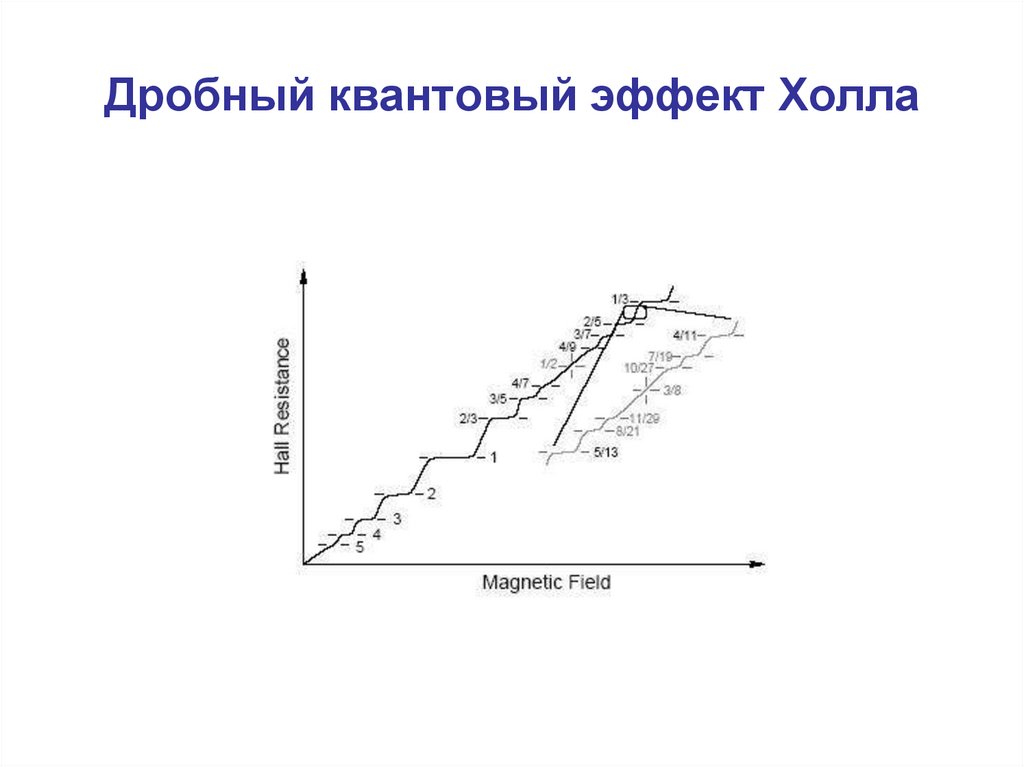
16. Дробный квантовый эффект Холла

17. Квазичастицы с зарядом e/3

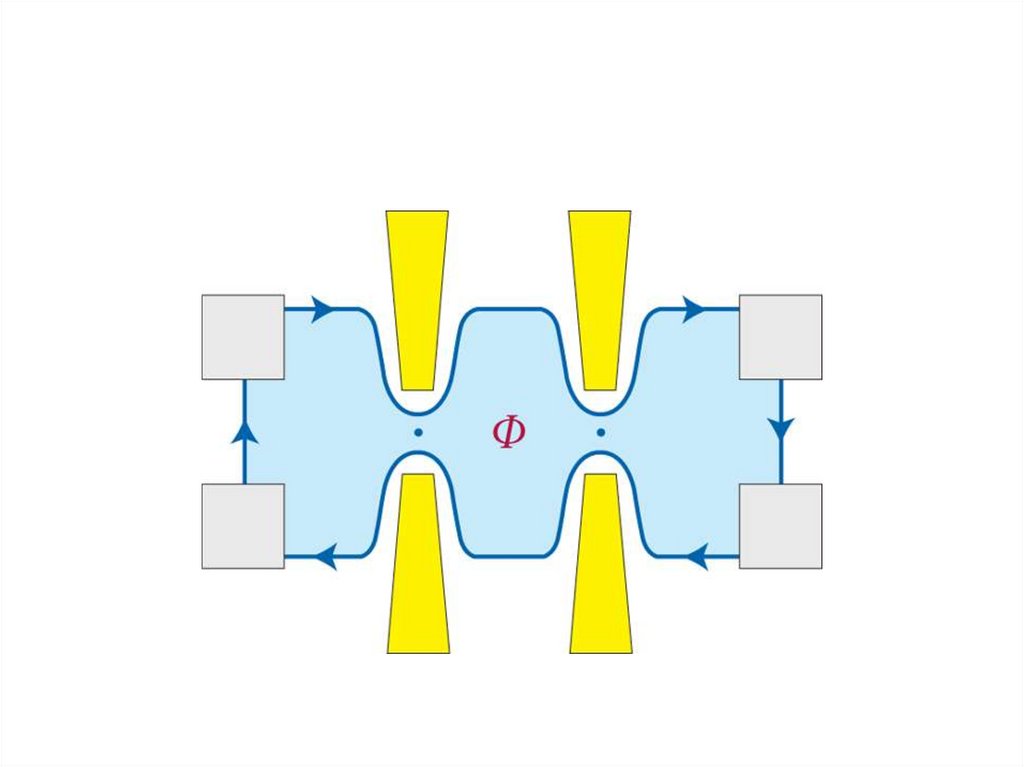
18. Эффект Ааронова-Бома

http://blog.jessriedel.com/wp-content/uploads/2014/06/ab-effect1.png

19. Композитные фермионы

20. Топологические изоляторы и токовые состояния

Инвариантность относительно
деформаций – топология!

21. Формула Гаусса-Бонэ и топология

https://slideplayer.com/slide/3362221/12/images/14/Gauss-Bonnet+Theorem+For+a+closed+surface+M%3A.jpg

22. Формула Гаусса-Бонэ и топология

https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcRc23VcoW1nGOTBIFEReUMxeVzGQDft1PqVFSpfUcvfWuMlttJG

23. Композитные фермионы

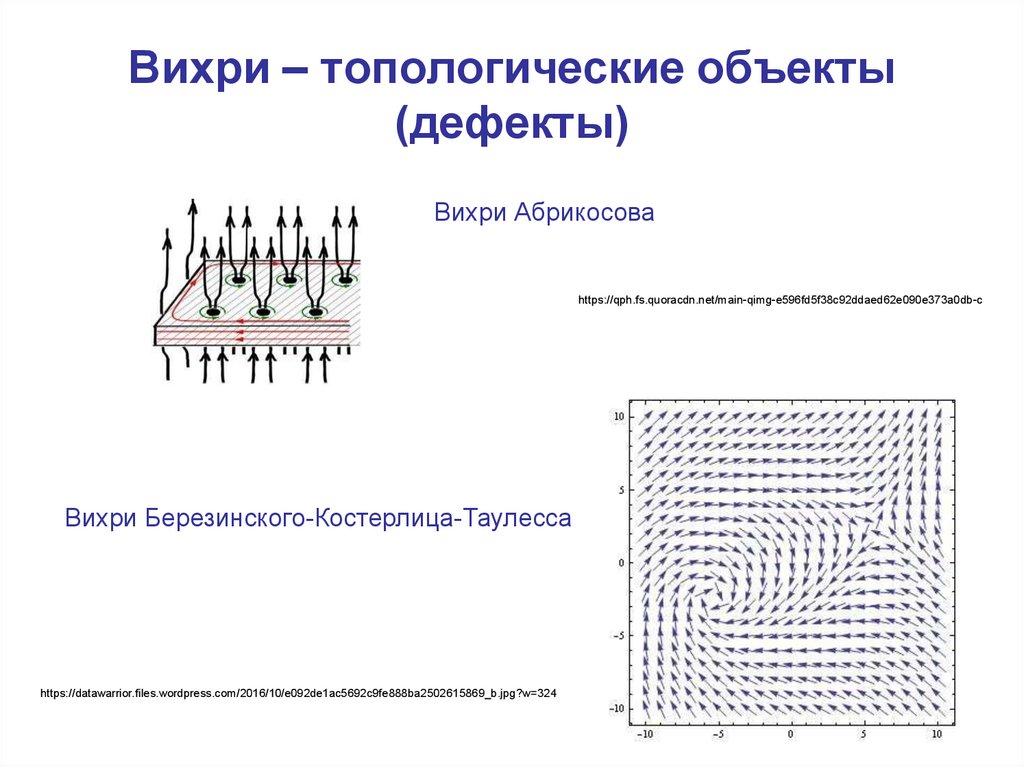
24. Вихри – топологические объекты (дефекты)

Вихри Абрикосова
https://qph.fs.quoracdn.net/main-qimg-e596fd5f38c92ddaed62e090e373a0db-c
Вихри Березинского-Костерлица-Таулесса
https://datawarrior.files.wordpress.com/2016/10/e092de1ac5692c9fe888ba2502615869_b.jpg?w=324

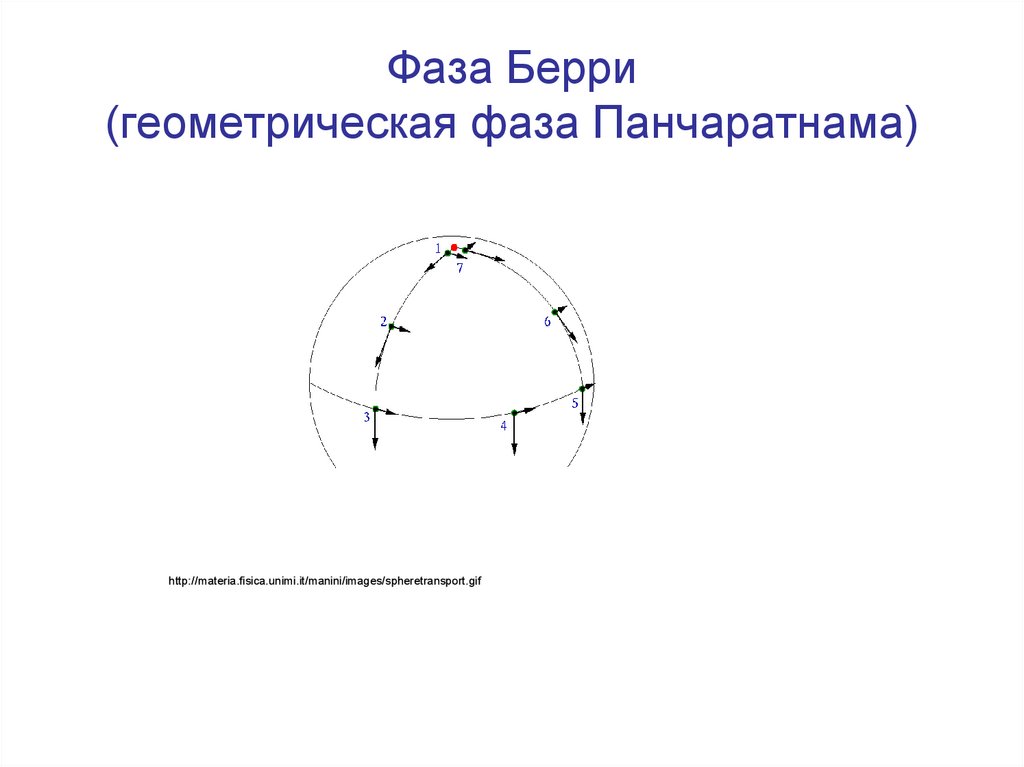
25. Фаза Берри (геометрическая фаза Панчаратнама)

http://materia.fisica.unimi.it/manini/images/spheretransport.gif

26. Как устроена материя и чем она отличается от вакуума?

Атомы, ионы и электроны –
УПОРЯДОЧЕНЫ

27. Как устроена материя и чем она отличается от вакуума?

Атомы, ионы и электроны –
УПОРЯДОЧЕНЫ
Упорядочение обладает определенной
СИММЕТРИЕЙ – 6 сингоний, 7
кристаллических систем, 32 точечные
группы, 230 пространственных групп

28. Как устроена материя и чем она отличается от вакуума?

Дополнительный элемент симметрии –
обращение времени t
В магнетиках t-инвариантность нарушена
Всего существует 122 кристаллографических
магнитных класса и 1651 магнитная
(шубниковская) группа

29. Концепция нарушения симметрии Ландау

В твердых телах нарушена (по
отношению к вакууму) трансляционная
и вращательная симметрии
В магнетиках – симметрия по
отношению к обращению времени
В сверхпроводниках – калибровочная
симметрия (функционал ГинзбургаЛандау)

30. Концепция нарушения симметрии Ландау

В твердых телах нарушена (по
отношению к вакууму) трансляционная
и вращательная симметрии
В магнетиках – симметрия по
отношению к обращению времени
В сверхпроводниках – калибровочная
симметрия (функционал ГинзбургаЛандау)
Малые изменения параметров
существенны!

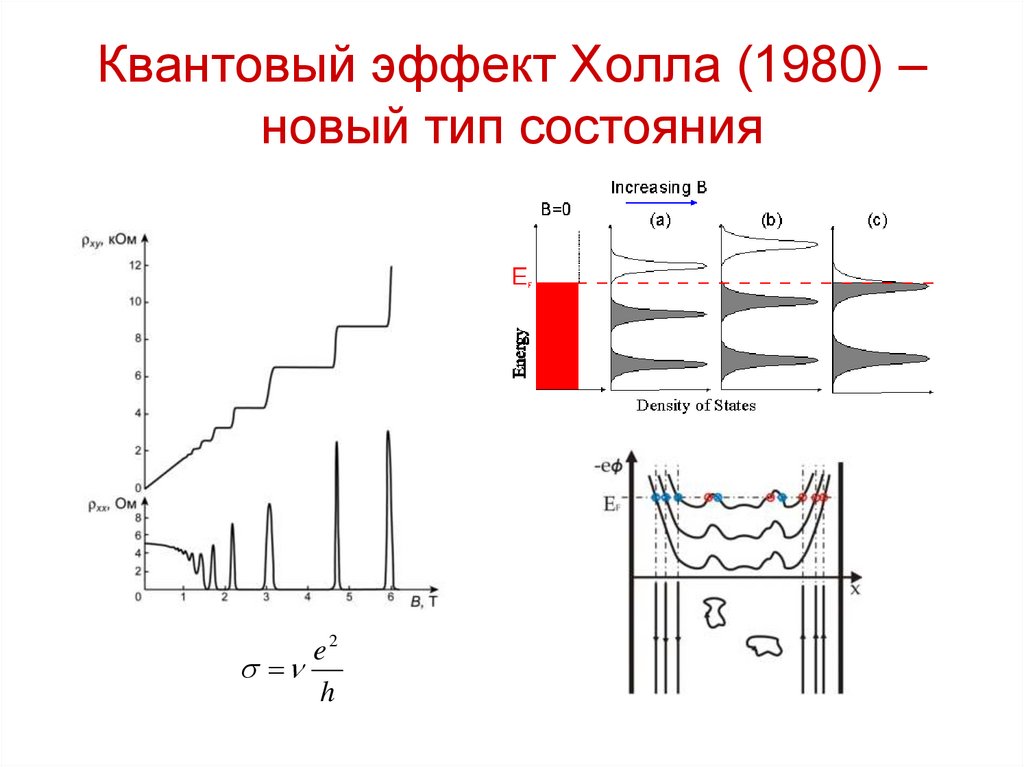
31. Квантовый эффект Холла (1980) – новый тип состояния

e2
h

32. Формула Гаусса-Бонэ и топология

https://slideplayer.com/slide/3362221/12/images/14/Gauss-Bonnet+Theorem+For+a+closed+surface+M%3A.jpg

33. Формула Гаусса-Бонэ и топология

https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcRc23VcoW1nGOTBIFEReUMxeVzGQDft1PqVFSpfUcvfWuMlttJG

34.

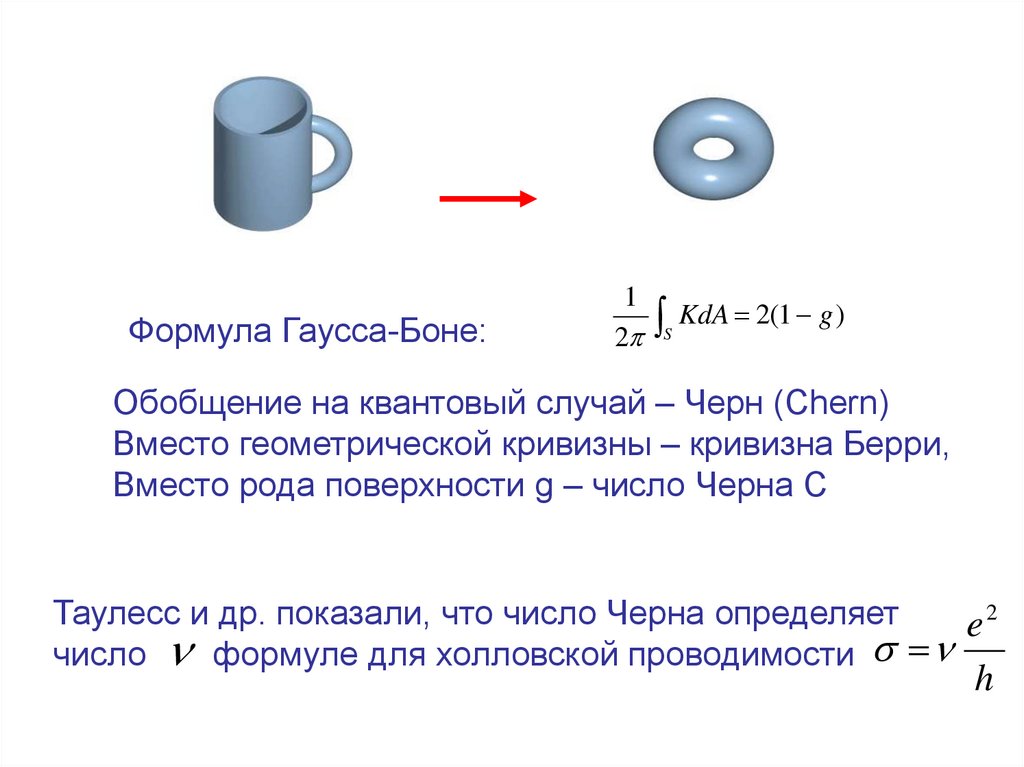
Формула Гаусса-Боне:
1
KdA 2(1 g )
2 S
Обобщение на квантовый случай – Черн (Chern)
Вместо геометрической кривизны – кривизна Берри,
Вместо рода поверхности g – число Черна C
Таулесс и др. показали, что число Черна определяет
e2
число формуле для холловской проводимости
h

35. Холловская проводимость как топологический инвариант

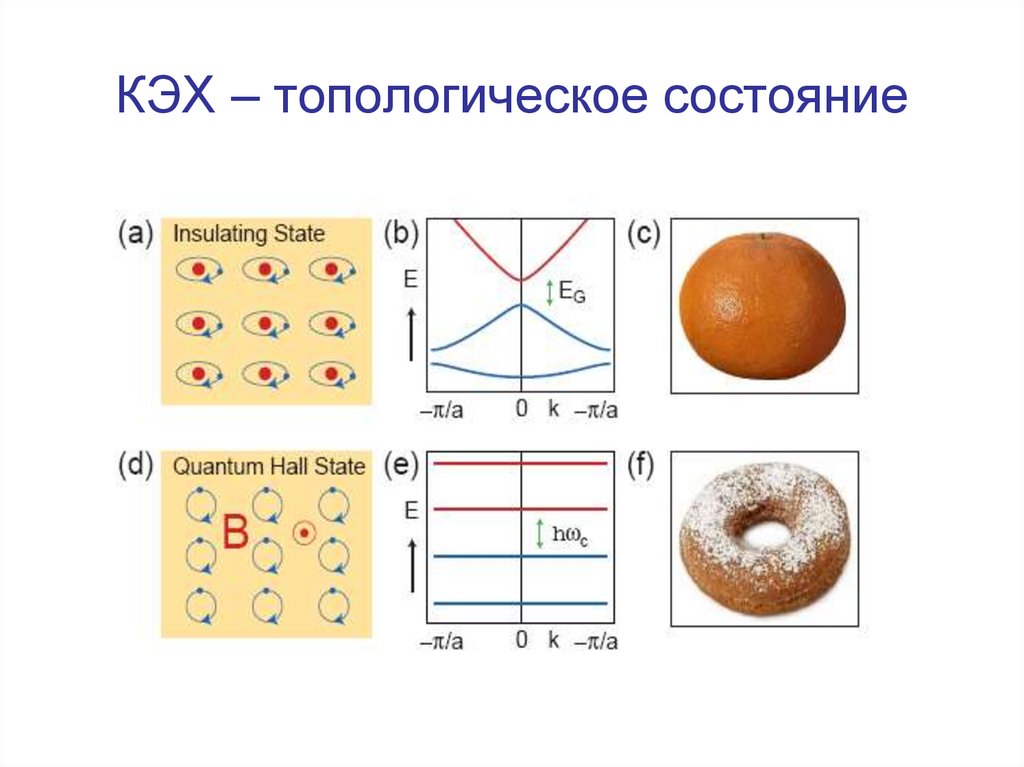
36. КЭХ – топологическое состояние

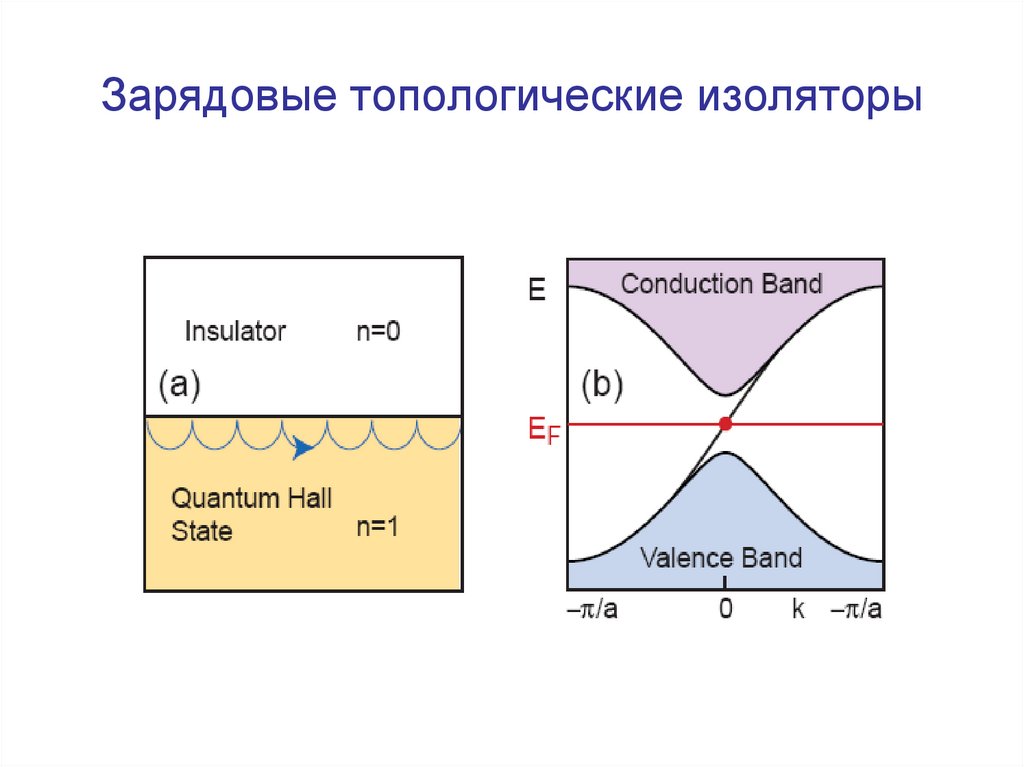
37. Зарядовые топологические изоляторы

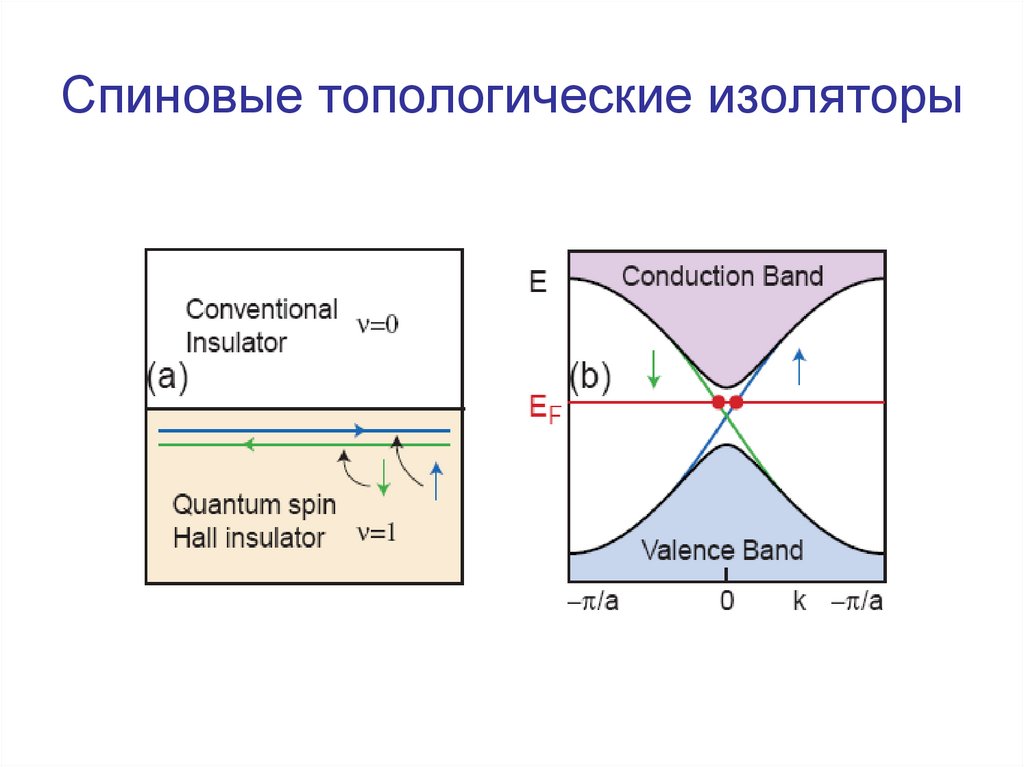
38. Спиновые топологические изоляторы

39. Спиновые топологические изоляторы

40.

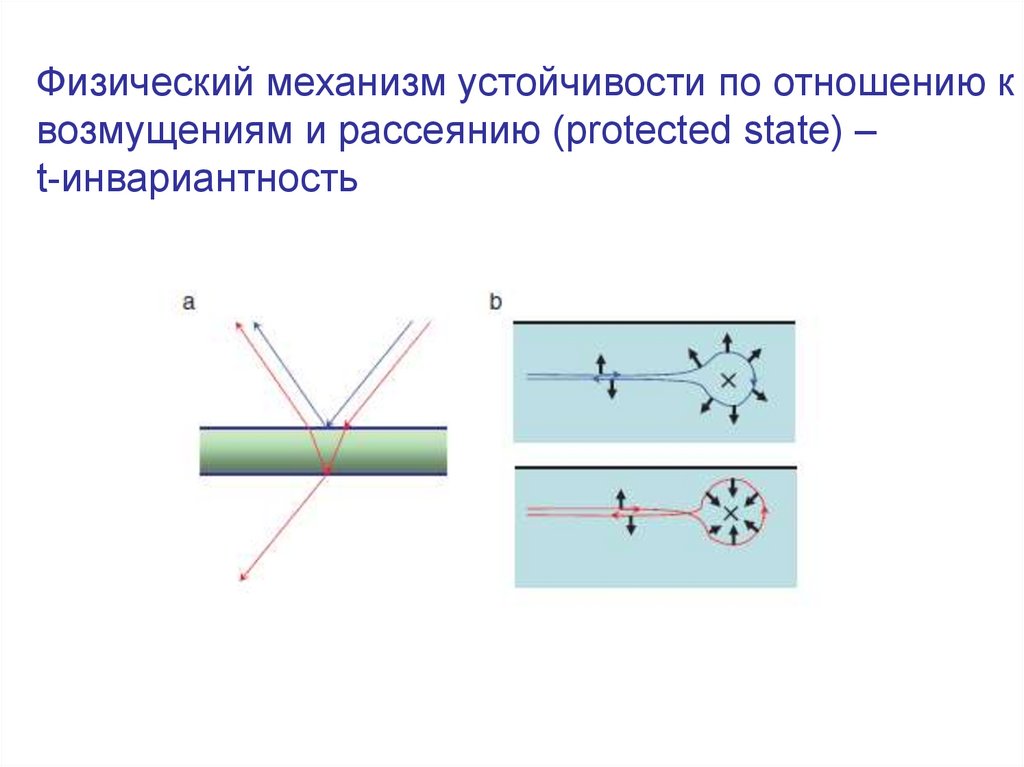
Физический механизм устойчивости по отношению к
возмущениям и рассеянию (protected state) –
t-инвариантность

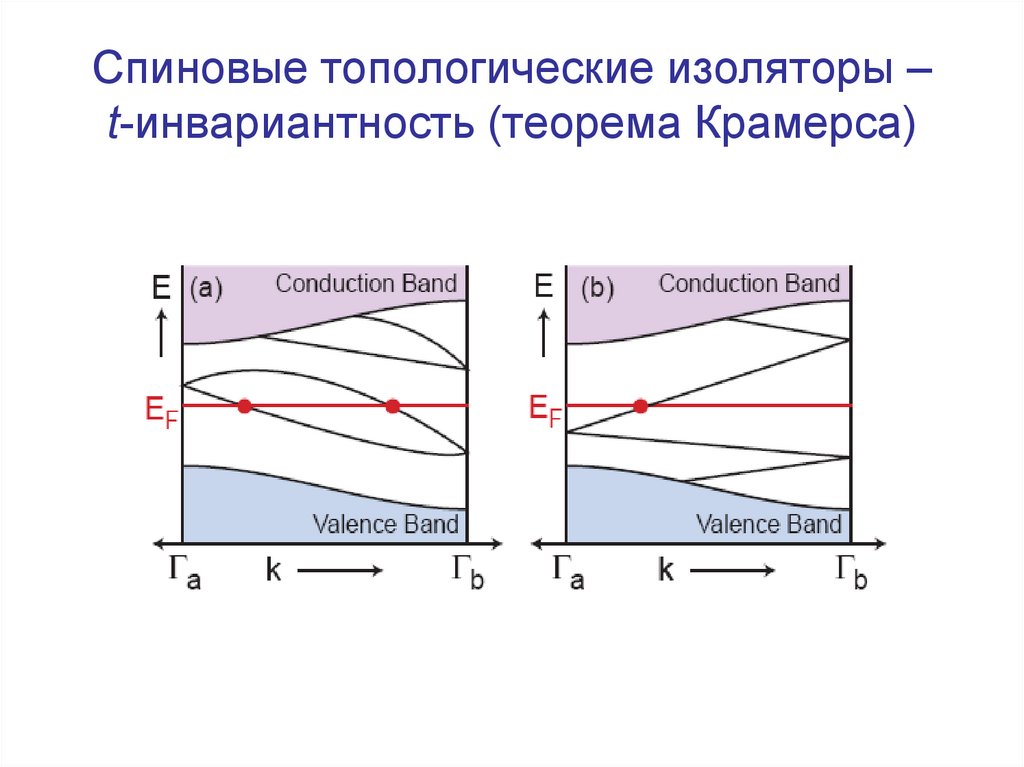
41. Спиновые топологические изоляторы – t-инвариантность (теорема Крамерса)

42.

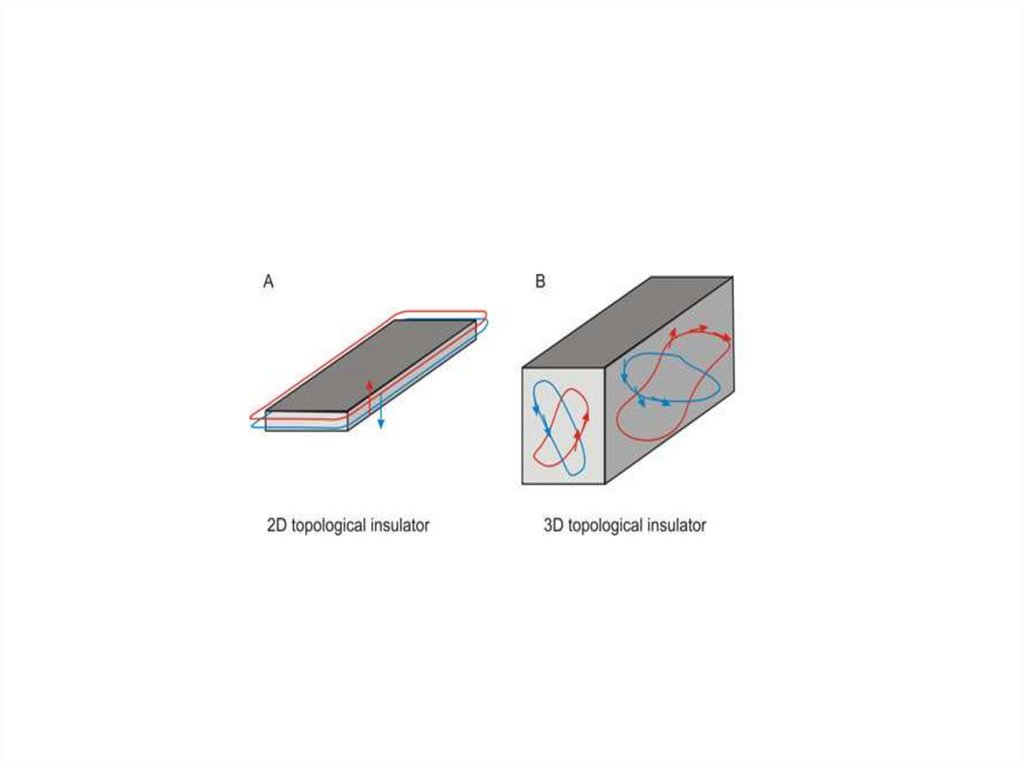
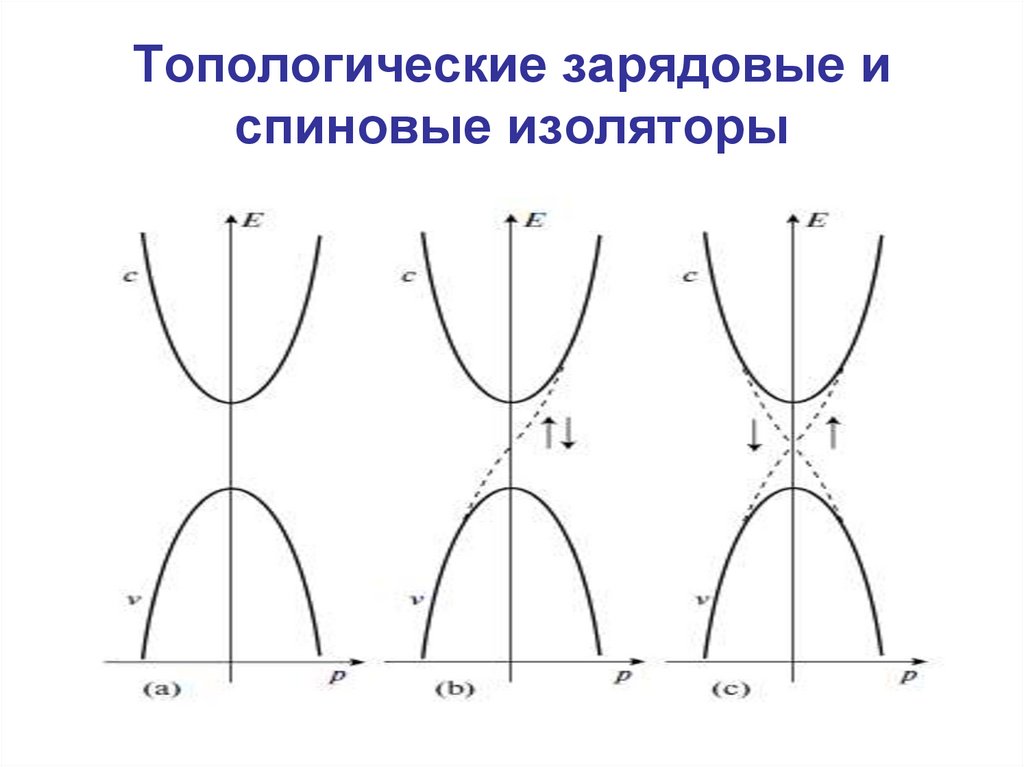
43. Топологические зарядовые и спиновые изоляторы

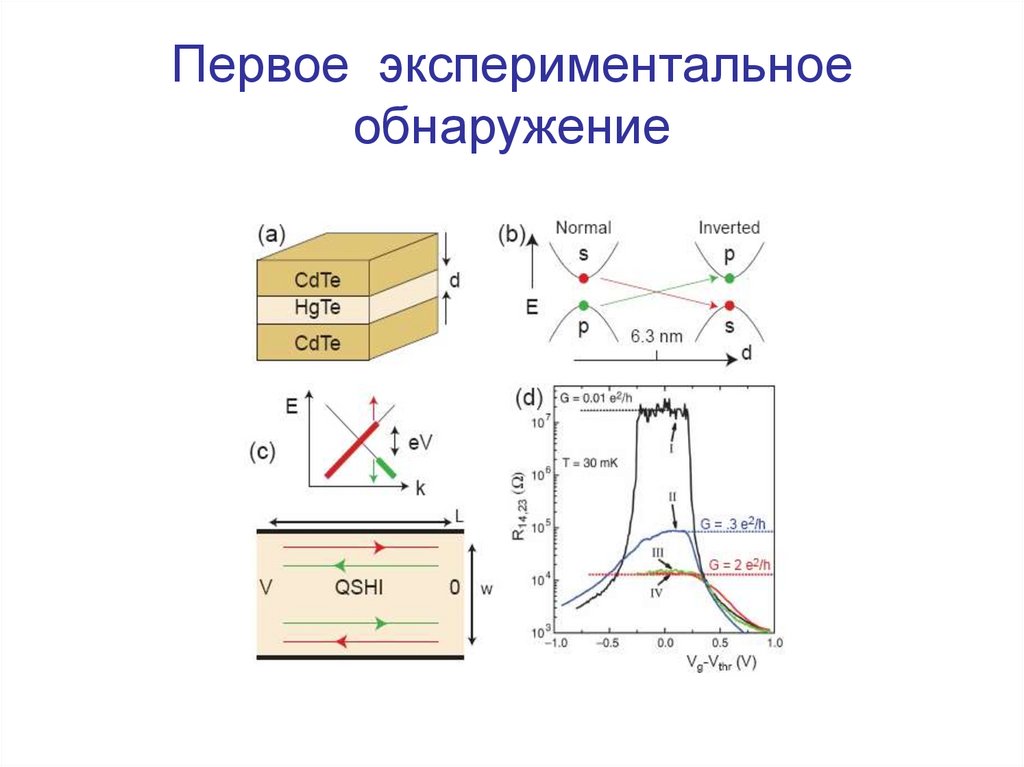
44. Первое экспериментальное обнаружение

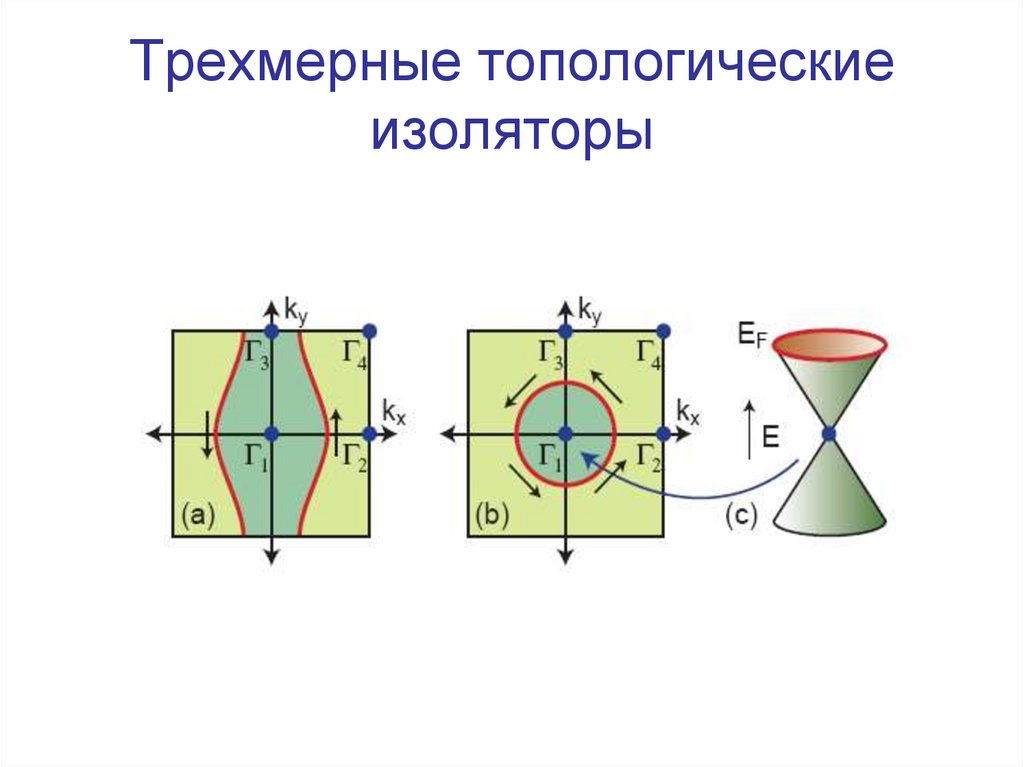
45. Трехмерные топологические изоляторы

46.

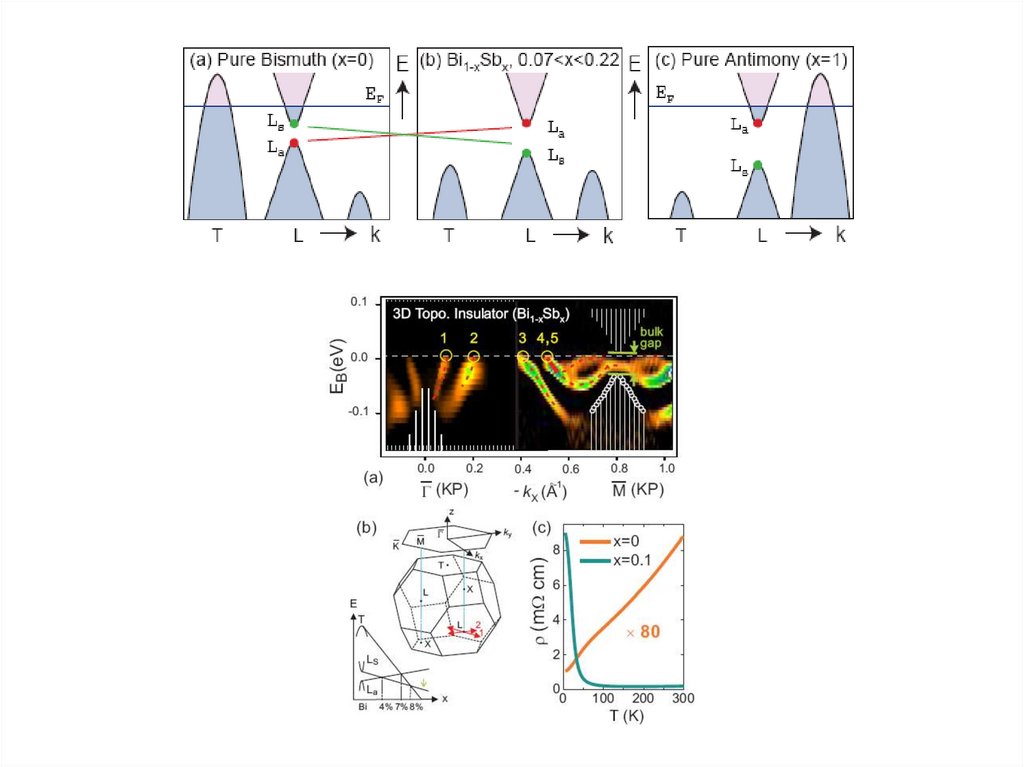
47. Трехмерные топологические изоляторы

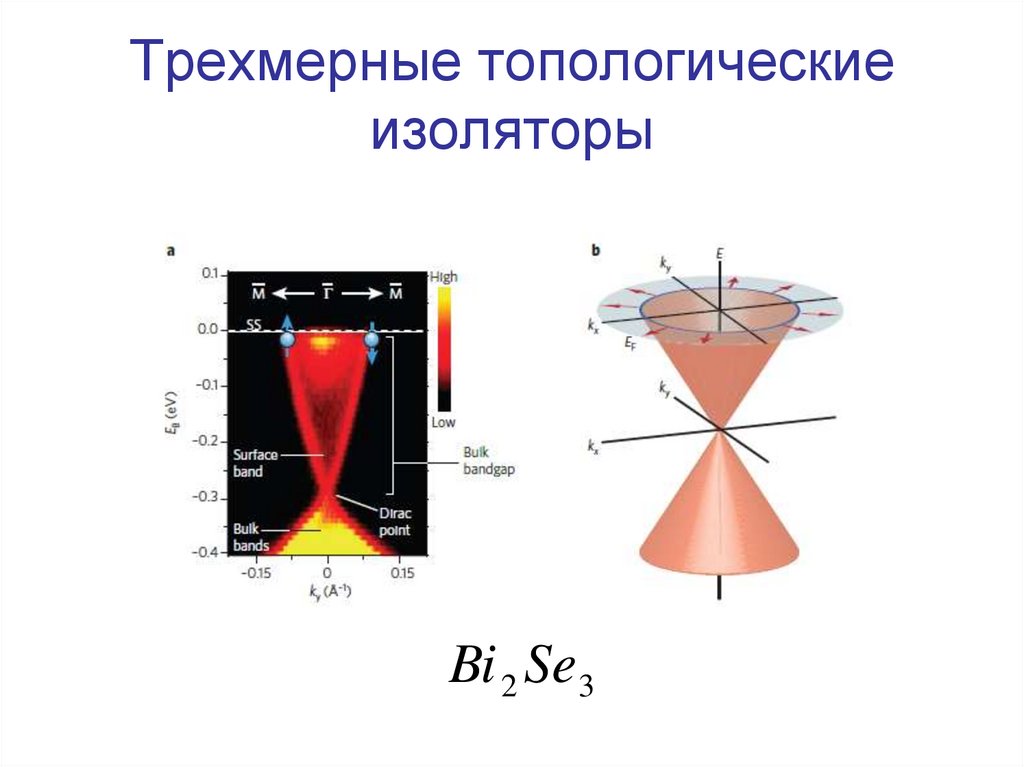
Bi 2 Se 3

48.

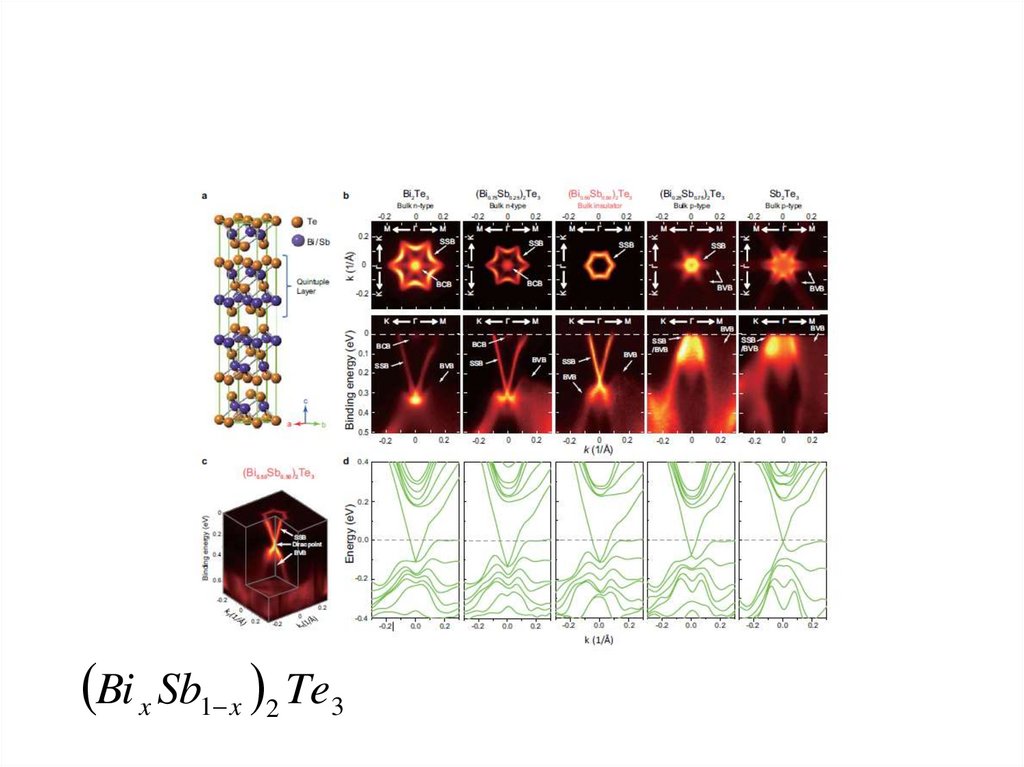
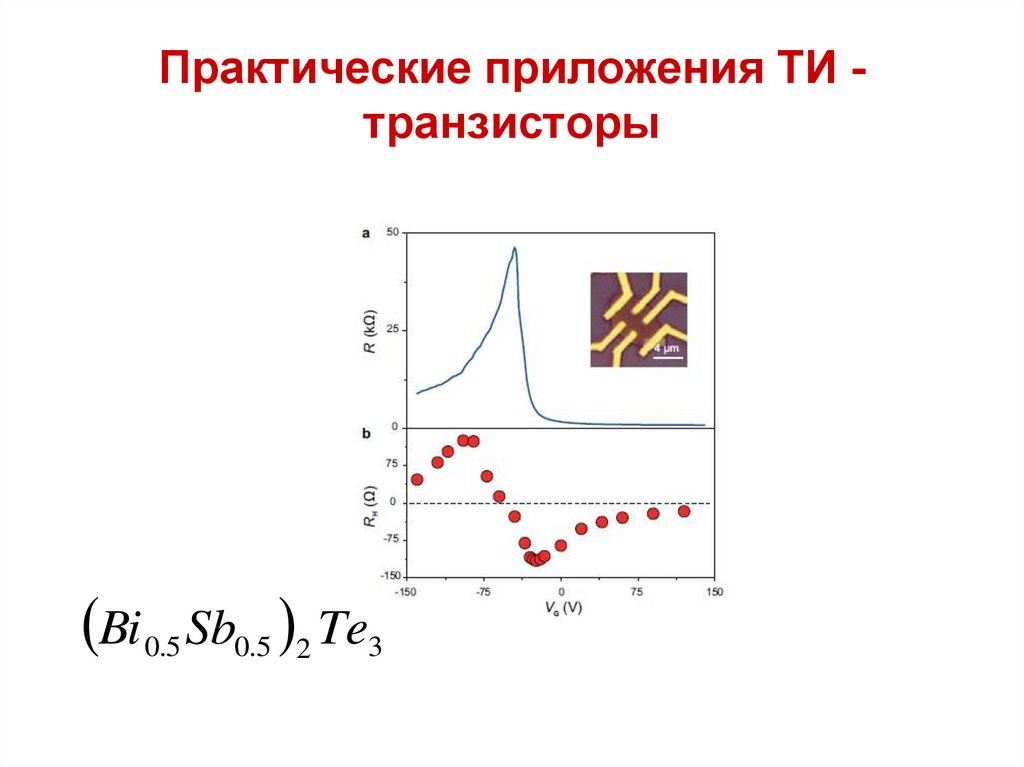
Bi x Sb1 x 2 Te3

49. Практические приложения ТИ - транзисторы

Практические приложения ТИ транзисторы
Bi 0.5 Sb0.5 2 Te3

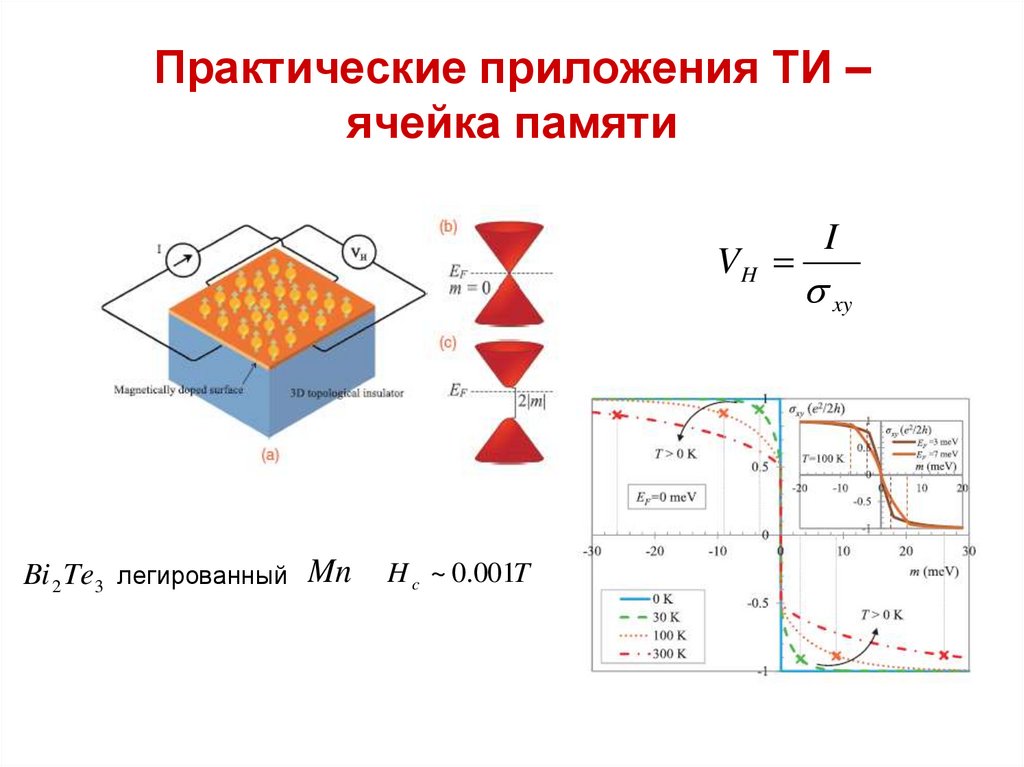
50. Практические приложения ТИ – ячейка памяти

VH
Bi 2 Te3 легированный Mn
H c ~ 0.001T
I
xy

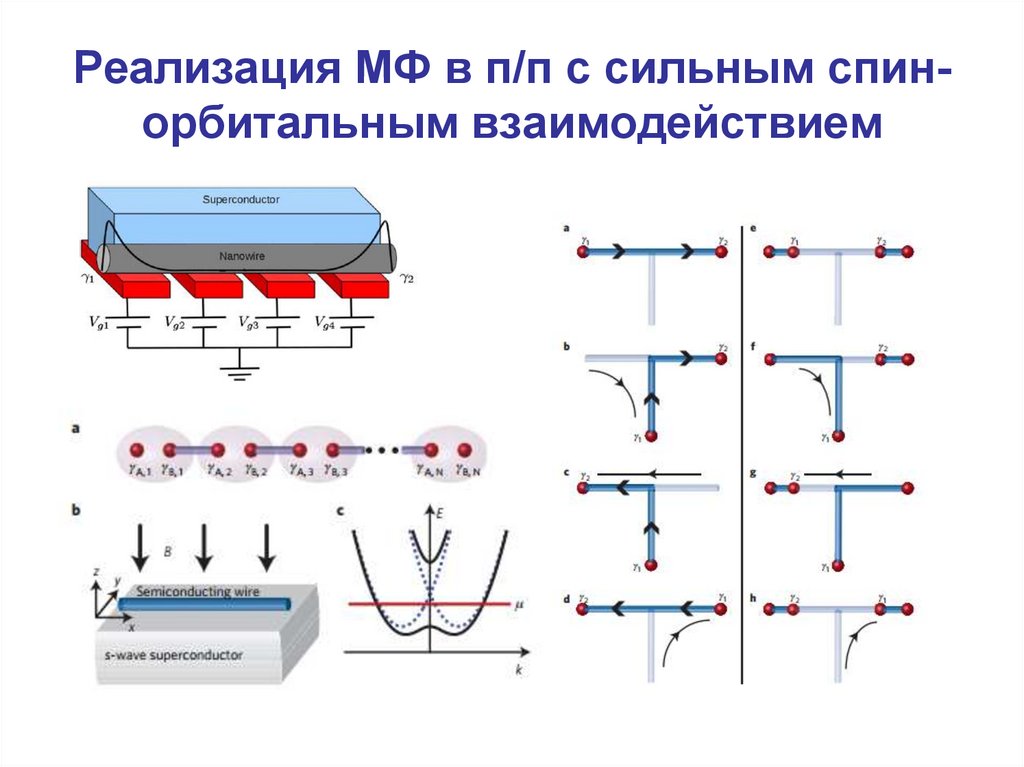
51. Практические приложения ТИ – фермионы Майораны и квантовые вычисления

Уравнение Дирака:
i m 0
- античастица
Уравнение Майораны
i ~ m 0
Сверхпроводники
p x ip y
E 0
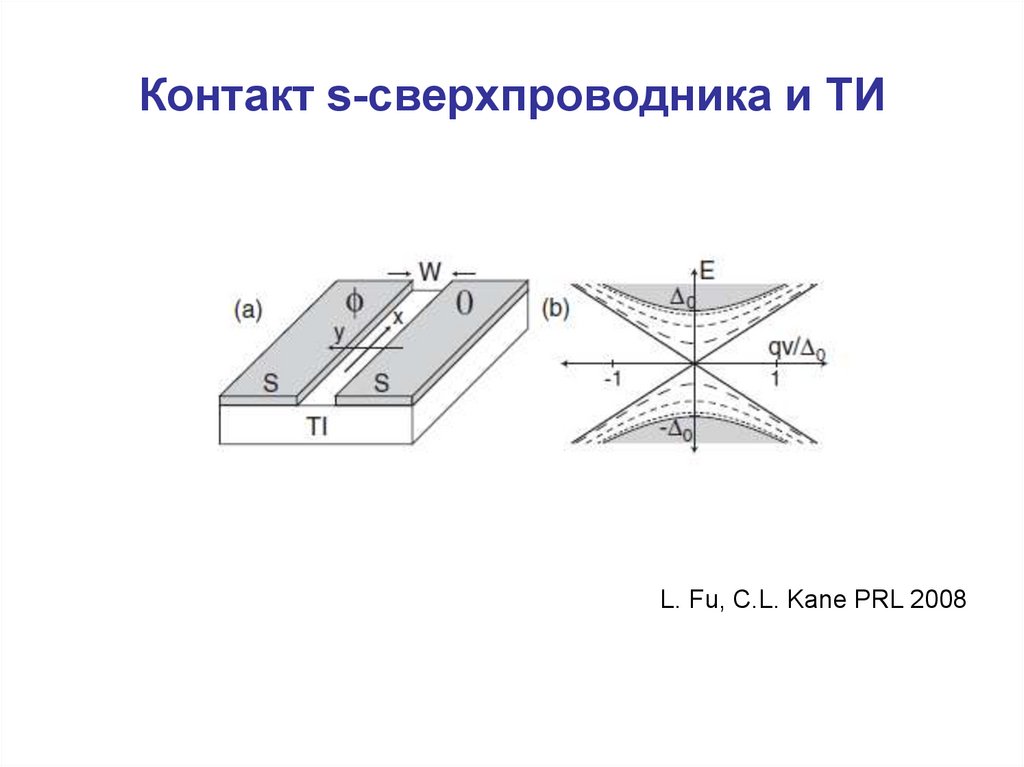
Контакт нормального сверхпроводника и ТИ

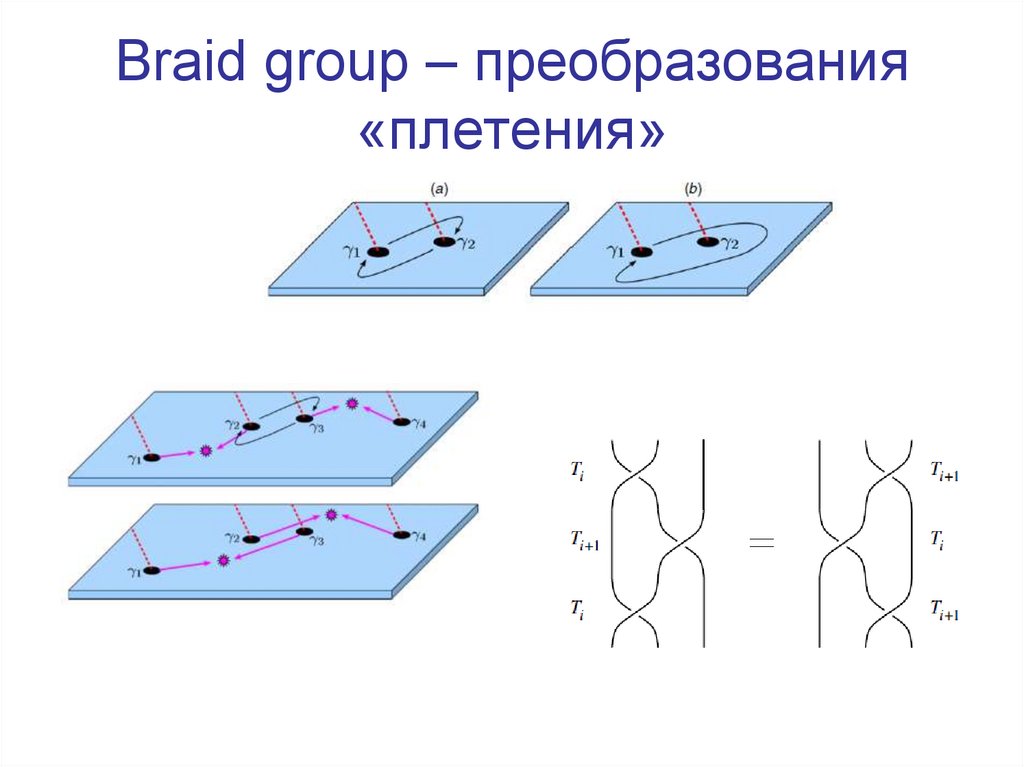
52. Природа нелокальности

N
N 1
i 1
i 1
Hˆ ni tci c i 1 c i c i 1 h.c .
1
1
с i ( i ,1 i i , 2 ), с i ( i ,1 i i , 2 )
2
2
N 1
N 1
i 1
i 1
Hˆ chain it i , 2 i 1,1 2t c~i c~i , c~i ( i 1,1 i i , 2 ) / 2
c~M ( 1,1 i N , 2 ) / 2,
E0 0
Нулевая мода!

53. Braid group – преобразования «плетения»

54. Контакт s-сверхпроводника и ТИ

L. Fu, C.L. Kane PRL 2008

55. Реализация МФ в п/п с сильным спин-орбитальным взаимодействием

Реализация МФ в п/п с сильным спинорбитальным взаимодействием