Similar presentations:
Математическая модель
1. Математическая модель
2.
Перевести на языкматематики следующие
выражения:
1)Сумма удвоенного числа
а и утроенного числа b
2)Произведение суммы
чисел a и b и числа 10
3)Частное разности чисел а
и х и суммы чисел b и 5
3.
Проверка:1)2а + 3b
2)(а + b)10
3)(а - х) : ( b+ 5)
4.
Ученик каменщика укладываетза 1 час n кирпичей
Каменщик укладывает
в 5 раз больше
Записать на математическом языке:
1)За 3 часа каменщик и его ученик уложили 360
кирпичей
2) Ученик работал 3 часа, а каменщик - 6 часов, и за это
время уложил на 540 кирпичей больше, чем его ученик
3)Число кирпичей, которые уложил каменщик за 3 часа,
меньше 350
4) Число кирпичей, которые уложил ученик за 3 часа,
больше 50
5.
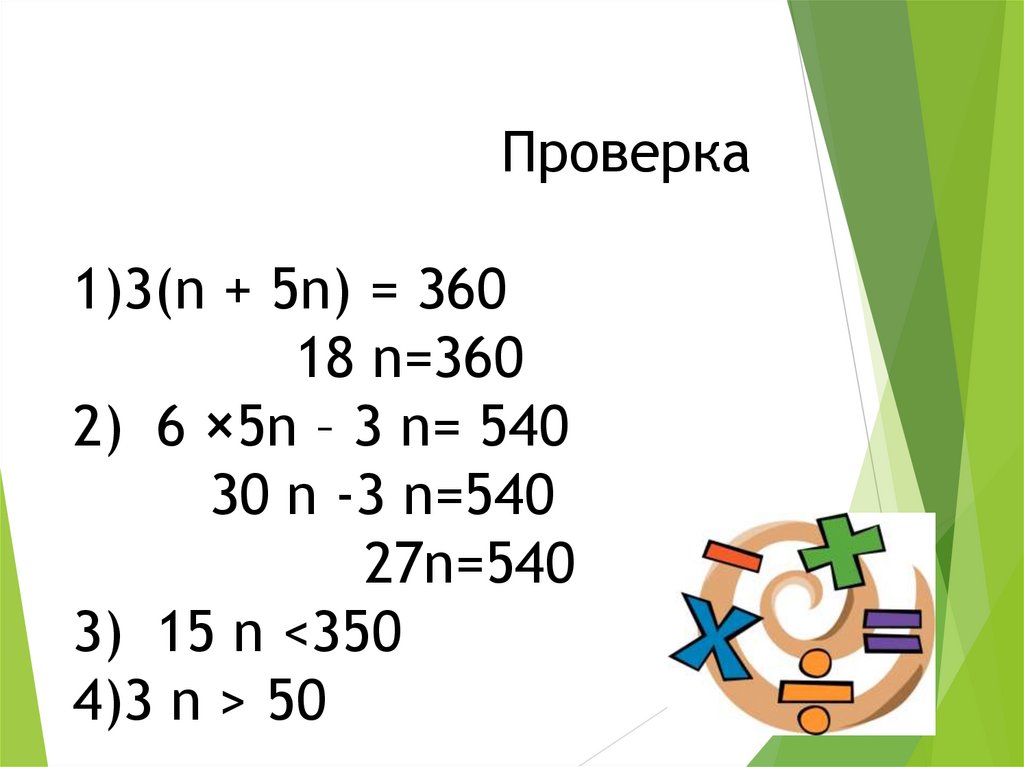
Проверка1)3(n + 5n) = 360
18 n=360
2) 6 ×5n – 3 n= 540
30 n -3 n=540
27n=540
3) 15 n <350
4)3 n > 50
6. Реальная ситуация
В школе четыре седьмых класса. В 7А учатся 15 девочек и13 мальчиков, в 7Б – 12 девочек и 12 мальчиков, в 7В – 9
девочек и 18 мальчиков, в 7Г классе – 20 девочек и 10
мальчиков. Сколько учеников в каждом из седьмых
классов.
в 7А
в 7Б
в 7В
в 7Г
15 + 13 = 28 учеников;
12 + 12 = 24 ученика;
9 + 18 = 27 учеников;
20 + 10 = 30 учеников.
7. Математическая модель
Используя математический язык, можно все этичетыре разные ситуации объединить: в классе учатся
a девочек и b мальчиков, значит, всего учеников a + b
. Эту запись a + b называют математической
моделью данной реальной ситуации.
8. Алгебра и математические модели
Алгебра в основном занимается тем, что описываетразличные реальные ситуации на математическом
языке в виде математических моделей, а затем
имеет дело уже не с реальными ситуациями, а с этими
моделями, используя разные правила, свойства,
законы, выработанные в алгебре.
9. От реальной ситуации к математической модели
a=ba = 2b
a+1=b+3
b = 3(a – 3)
10. В обратном направлении
Что означает (при тех же обозначениях, что и втаблице) такая математическая модель
a–5=b+5?
Ответ: Если из класса уйдут 5 девочек и
придут 5 мальчиков, то девочек и мальчиков в
классе станет поровну.
11. Задача
В классе девочек вдвое больше, чем мальчиков. Если из этогокласса уйдут три девочки и придут три мальчика, то девочек будет
на 4 больше, чем мальчиков. Сколько учеников в данном классе?
Решение. Пусть х – число мальчиков в классе, тогда 2х – число девочек.
Если уйдут три девочки, то останется (2х – 3) девочек. Если придут три
мальчика, то станет (х + 3) мальчиков. По условию девочек будет тогда на
4 больше, чем мальчиков; на математическом языке это записывается так:
(2х – 3) – (х + 3) = 4.
Это уравнение – математическая модель задачи. Используя известные
правила решения уравнений, последовательно получаем:
2х – 3 – х – 3 = 4 (раскрыли скобки);
х – 6 = 4 (привели подобные слагаемые);
х = 6 + 4;
х = 10.
Теперь мы можем ответить на вопрос задачи. В классе 10 мальчиков, а
значит, 20 девочек (вы помните, их по условию было в 2 раза больше).
Ответ: всего в классе 30 учеников.
12. Три этапа решения задачи
На первом этапе, введя переменную х и переведя текстзадачи на математический язык, мы составили
математическую модель – в виде уравнения
(2х – 3) – (х + 3) = 4.
На втором этапе, используя наши знания, мы это уравнение
решили, точнее, довели до самого простого вида (х = 10). На
этом этапе мы не думали ни про девочек, ни про мальчиков, а
занимались «чистой» математикой, работали только с
математической моделью.
На третьем этапе мы использовали полученное решение,
чтобы ответить на вопрос задачи. На этом этапе мы снова
вернулись к девочкам, мальчикам и интересующему нас классу.
13. Три этапа решения задачи
Первый этап. Составление математическоймодели.
Второй этап. Работа с математической
моделью.
Третий этап. Ответ на вопрос задачи.












 mathematics
mathematics








