Векторы. Равенство векторов

1.

Векторы
Подготовил: учитель математики
Шустова Т.В.

2.

Тема урока:
«Вектор»

3.

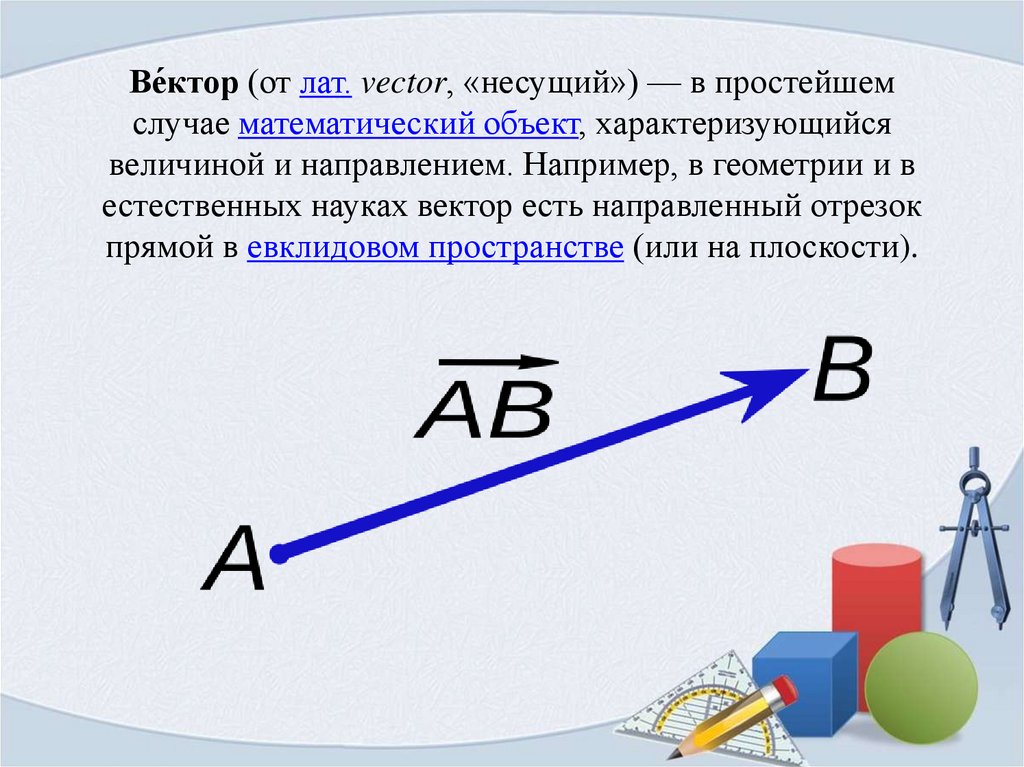
Ве́ктор (от лат. vector, «несущий») — в простейшем
случае математический объект, характеризующийся
величиной и направлением. Например, в геометрии и в
естественных науках вектор есть направленный отрезок
прямой в евклидовом пространстве (или на плоскости).

4.

Вектором мы будем называть направленный отрезок.
Направление вектора определяется указанием его начала и
конца. На чертеже направление вектора отмечается
стрелкой. Для обозначения векторов будем пользоваться
строчными латинскими буквами а, в, с… Можно также
обозначать вектор указанием его начала и конца. При этом
начало вектора ставится на первом месте. Вместо слова
«вектор» над буквенным обозначением вектора иногда
ставится стрелка или черта.

5.

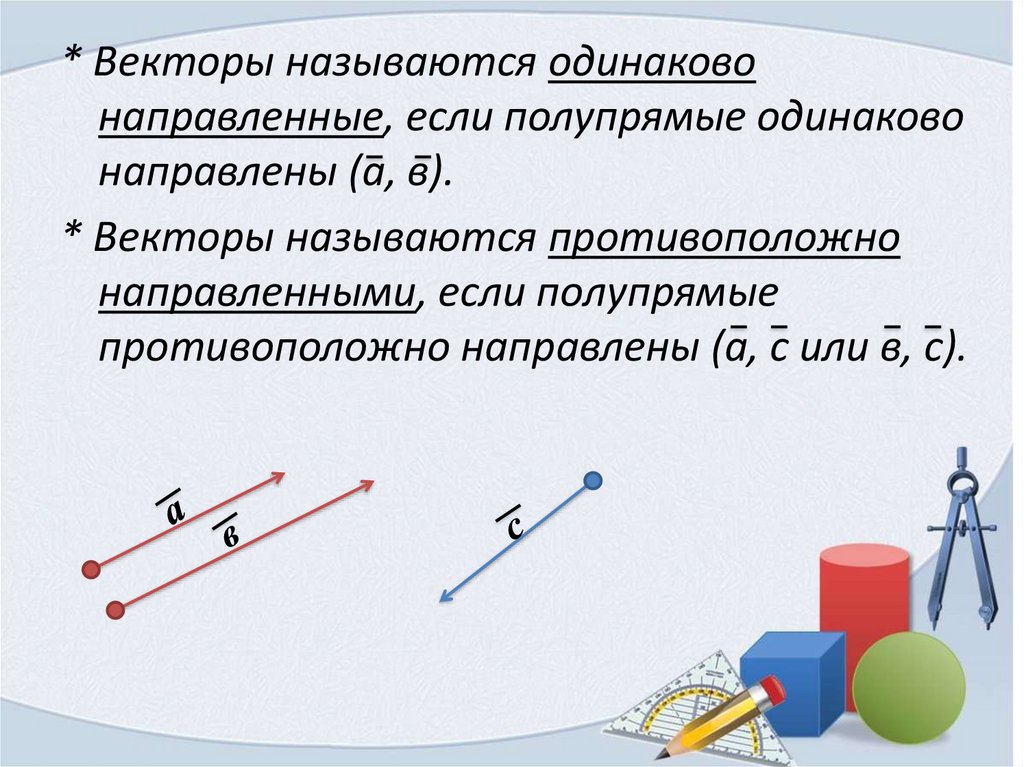
* Векторы называются одинаково
направленные, если полупрямые одинаково
направлены (а, в).
* Векторы называются противоположно
направленными, если полупрямые
противоположно направлены (а, с или в, с).

6.

Абсолютной величиной (или модулем) вектора называется
длина отрезка, изображающая вектор. Абсолютная величина
вектора а обозначается |a|.
Начало вектора может совпадать с его концом. Такой вектор
будем называть нулевым вектором ( 0 ).

7.

Равенство векторов.
Два вектора называются равными, если они
совмещаются параллельным переносом.
Из данного определения равенства векторов
следует, что равные векторы одинаково
направлены и равны по абсолютной
величине. Обратно: если векторы
одинаково направлены и равны по
абсолютной величине, то они равны.

8.

Равенство векторов.
В
А
D
С
Рис. 213

9.

Координаты векторов.
Равные векторы имеют равные соответствующие
координаты. И обратно: если у векторов
соответствующие координаты равны, то векторы
равны.

10.

Сложение векторов.
Теорема 10.1
Каковы бы ни были точки А, В, С, имеет
место векторное равенство АВ+ВС=АС.
Доказательство:
Пусть А (х1 ; у1 ), В (х2; у2 ), С (х3 ; у3 ) – данные
точки. Вектор АВ имеет координаты х 2–х 1 , у2 -у1 ,
вектор ВС имеет координаты х3 –х 2 , у3 –у 2 .
Следовательно, вектор АВ+ВС имеет координаты
х 3 -х1 , у3–у 1 . А это есть координаты вектора АС.
Значит векторы АВ+ВС и АС равны.
Теорема доказана.
1

11.

Спасибо за внимание