Демонстрационный вариант контрольных измерительных материалов для проведения в 2019 году основного государственного экзамена

1.

Учитель математики МБОУ
«Косиновская ООШ»
Тараторкина Елена Алексеевна

2.

Демонстрационный вариант
контрольных измерительных материалов для проведения
в 2019 году основного государственного экзамена
по МАТЕМАТИКЕ
Решение:
Преобразуем функцию, приведем ее к какому-нибудь знакомому виду
уравнения линии.
Выпишем числитель, решим биквадратное уравнение, разложим
числитель на множители.
x4-13x2+36=(x2-4)(x2-9)=(x-2)(x+2)(x-3)(x+3).
Тогда,

3.

4.

-у
6
5
y 6
1 точка
2 точки
4
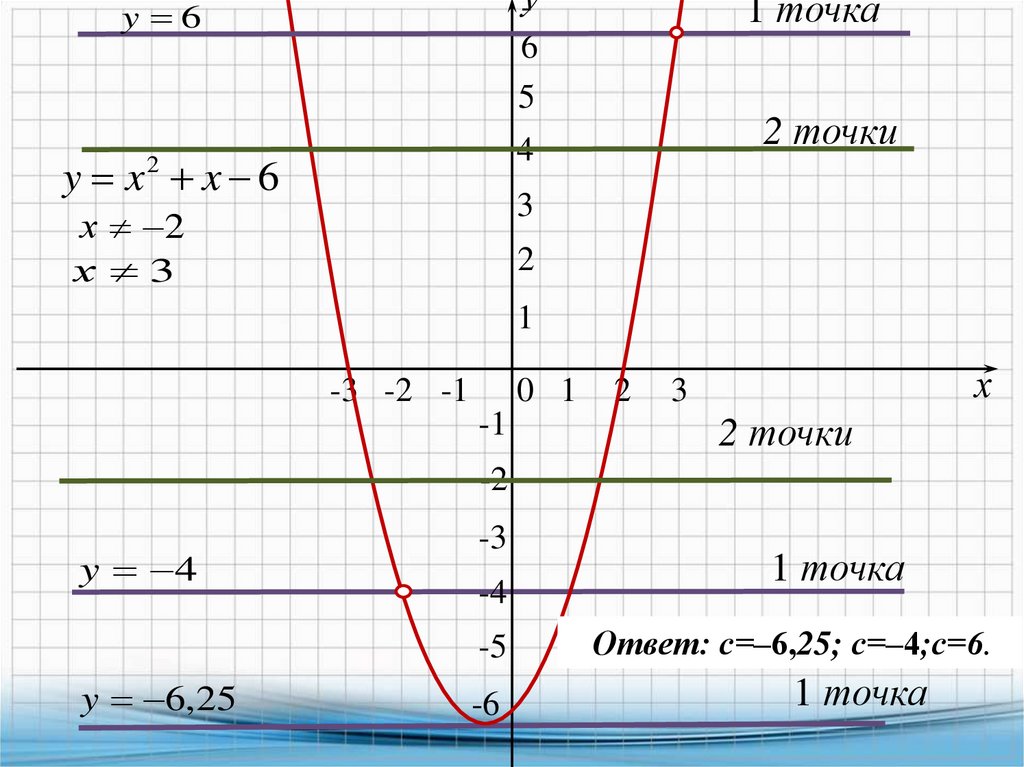
y x2 x 6
3
х 2
х 3
2
1
-3 -2 -1
0 1
-1
2
х
3
2 точки
-2
y 4
-3
-4
-5
y 6,25
-6
1 точка
Ответ: с=‒6,25; с=‒4;с=6.
1 точка

5.

.
Открытый банк заданий ОГЭ

6.

x 2
1. Постройте график функции y 1 2
x 2x
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x 2
y 1 2
x 2x
x 2
x 2
1
1 2
1
1
x 2x
x x 2
x
при условии х 0 и х 2 0
х 0 и х 2.

7.

у
1
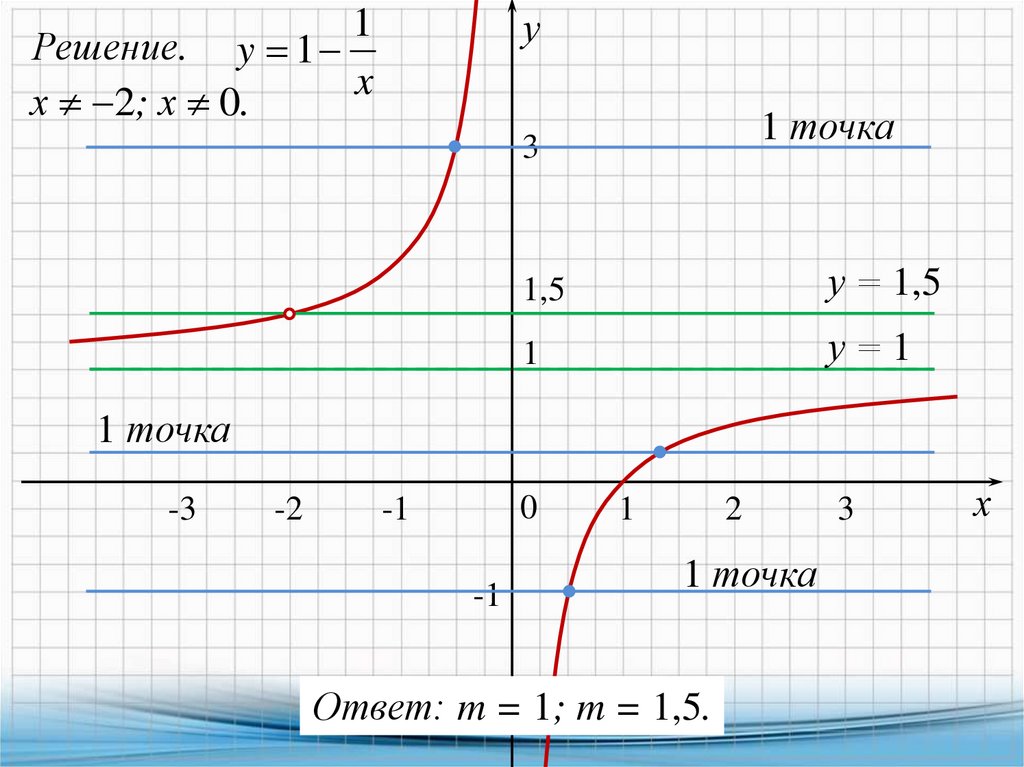
Решение. y 1
x
х 2; х 0.
1 точка
3
1,5
у = 1,5
1
у=1
1 точка
-3
-2
0
-1
-1
1
2
1 точка
Ответ: m = 1; m = 1,5.
3
х

8.

x x
2. Постройте график функции y 1
x x2
и определите, при каких значениях т прямая у = т
имеет с графиком две общие точки.
4
3
Решение.
x 4 x3
y 1
2
x x
4
3
3
x x
x x 1
2
1
1
1
x
x x2
x x 1
при условии х 0 и х 1 0
х 0 и х 1.

9.

у
2
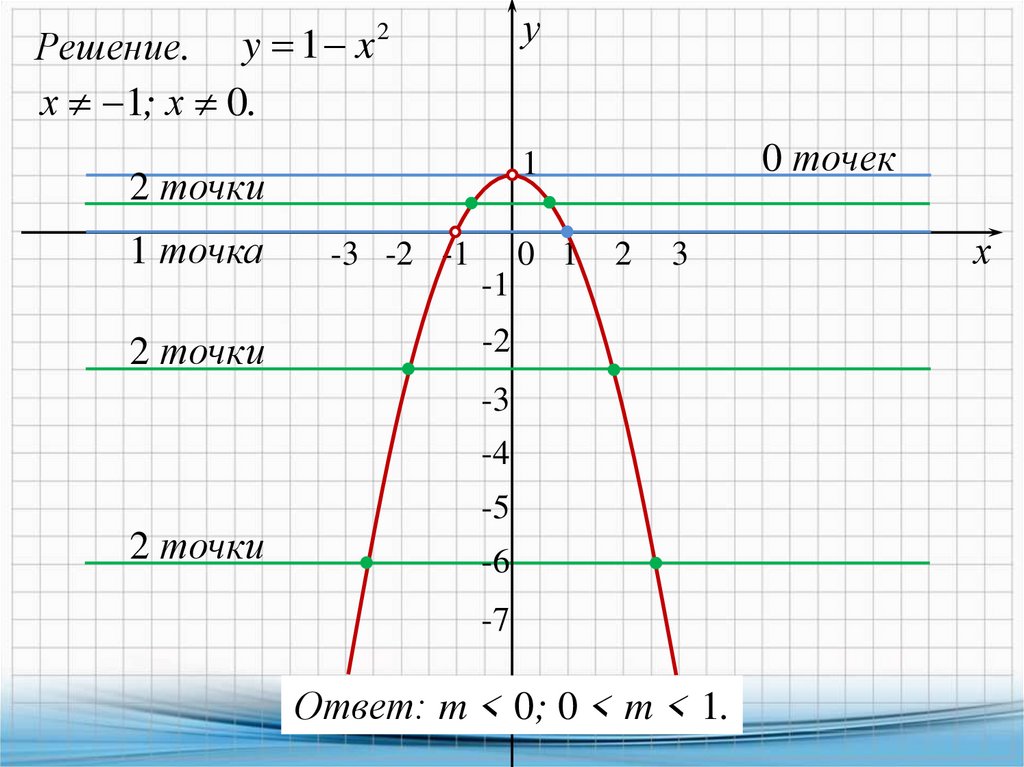
Решение. y 1 x
х 1; х 0.
2 точки
1 точка
2 точки
0 точек
1
-3 -2 -1
-1
0 1
2
3
-2
-3
-4
2 точки
-5
-6
-7
Ответ: m < 0; 0 < m < 1.
х

10.

3. Постройте график функции y x 2 6 x 8
Какое наибольшее число общих точек график данной функции
может иметь с прямой, параллельной оси абсцисс?
Решение.
Раскрывая модуль, получим, что график функции
можно представить следующим образом:
Построим квадратичные параболы, учитывая
область определения каждой функции.

11.

у
Решение.
8
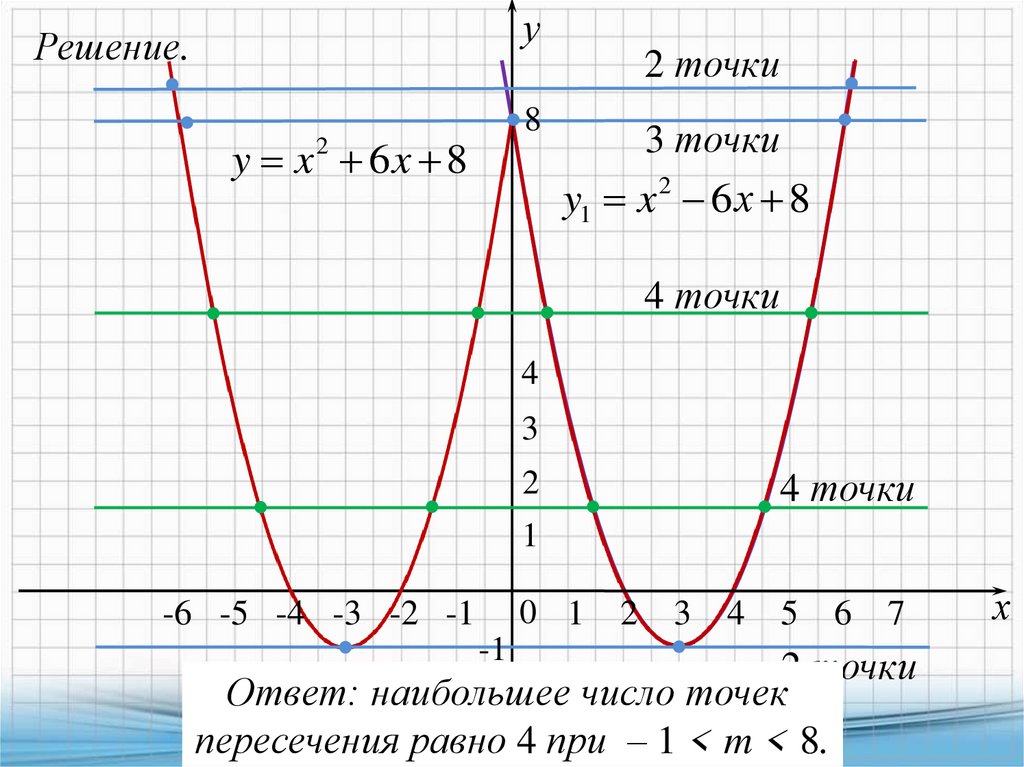
y x2 6x 8
2 точки
3 точки
y1 x 2 6 х 8
4 точки
4
3
4 точки
2
1
0 1
-6 -5 -4 -3 -2 -1
-1
2
3
4
5
6
7
2 точки
Ответ: наибольшее
число точек
-2
пересечения равно 4 при – 1 < m < 8.
х

12.

x
y
x 6 x2 4x 5
4. Постройте график функции
2
x 2x 3
и определите, при каких значениях т прямая у = т
имеет с графиком ровно одну общую точку.
Решение.
2
2
x x 6 x 4x 5
y
x2 2x 3
2
2
x x 6 x 4 x 5 x 3 x 2 x 1 x 5
2
x 1 x 3
x 2x 3
x 2 x 5 x 2 3x 10.
при условии х 1 0, х 3 0 х 1 и х 3.
2

13.

у
0 1
-4 -3 -2 -1
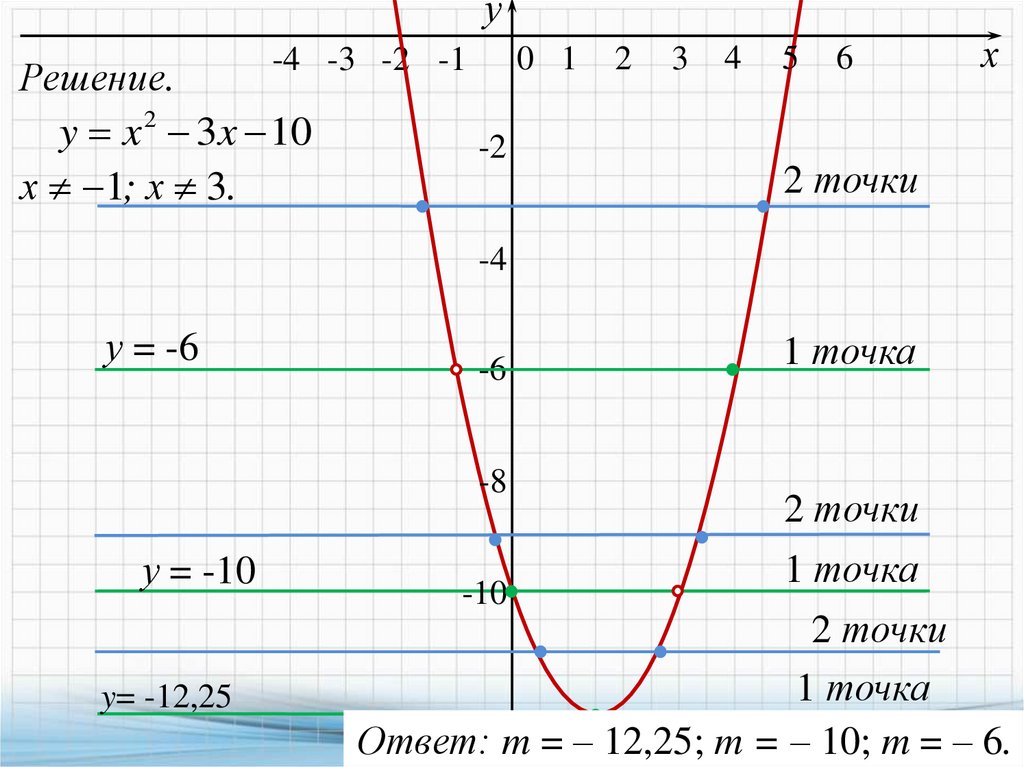
Решение.
y x 2 3x 10
х 1; х 3.
-2
2
3
4
5
6
х
2 точки
-4
у = -6
-6
-8
у = -10
y= -12,25
-10
1 точка
2 точки
1 точка
2 точки
1 точка
Ответ: m = ‒ 12,25; m = ‒ 10; m = ‒ 6.

14.

x 2 4 x 6, если х 1,
5. Постройте график функции y
3х, если х 1
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
x 2 4 x 6, если х 1,
y
3х, если х 1
y1 x 2 4 х 6
y2 3x
b
xв
2;
2a
yв 2 2 4 2 6 2.
x
y
0
0
-2
-6

15.

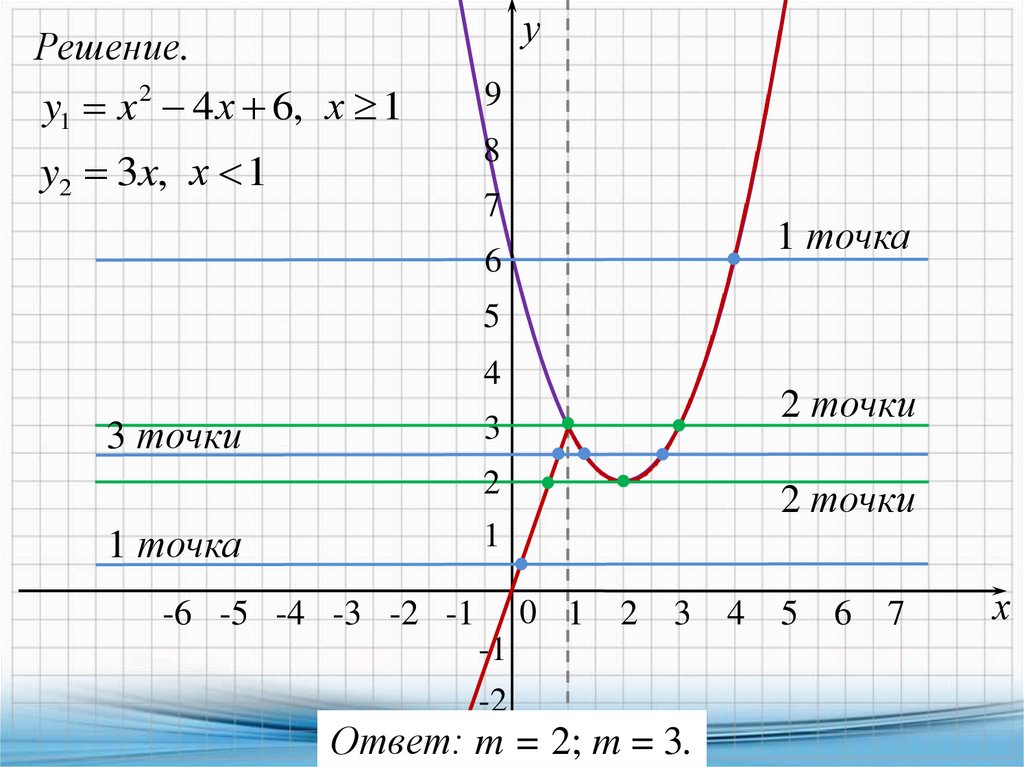
Решение.
2
y1 x 4 х 6, х 1
у
9
8
y2 3x, х 1
7
1 точка
6
5
4
3 точки
2 точки
3
2
1 точка
2 точки
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
-2
Ответ: m = 2; m = 3.
4
5
6
7
х

16.

6. Найдите все значения k, при каждом из которых прямая y = kx
имеет с графиком функции y = x2 + 4 ровно одну общую точку.
Постройте этот график и все такие прямые.
Решение.
Прямая y=kx имеет с графиком функции y = x2 + 4 ровно одну
общую точку, если уравнение
kx x 2 4 имеет один
корень. Такое возможно, когда дискриминант равен 0.
kx x 2 4
x 2 kx 4 0
D k 2 16
1 корень D 0 k 2 16 0 k 4.

17.

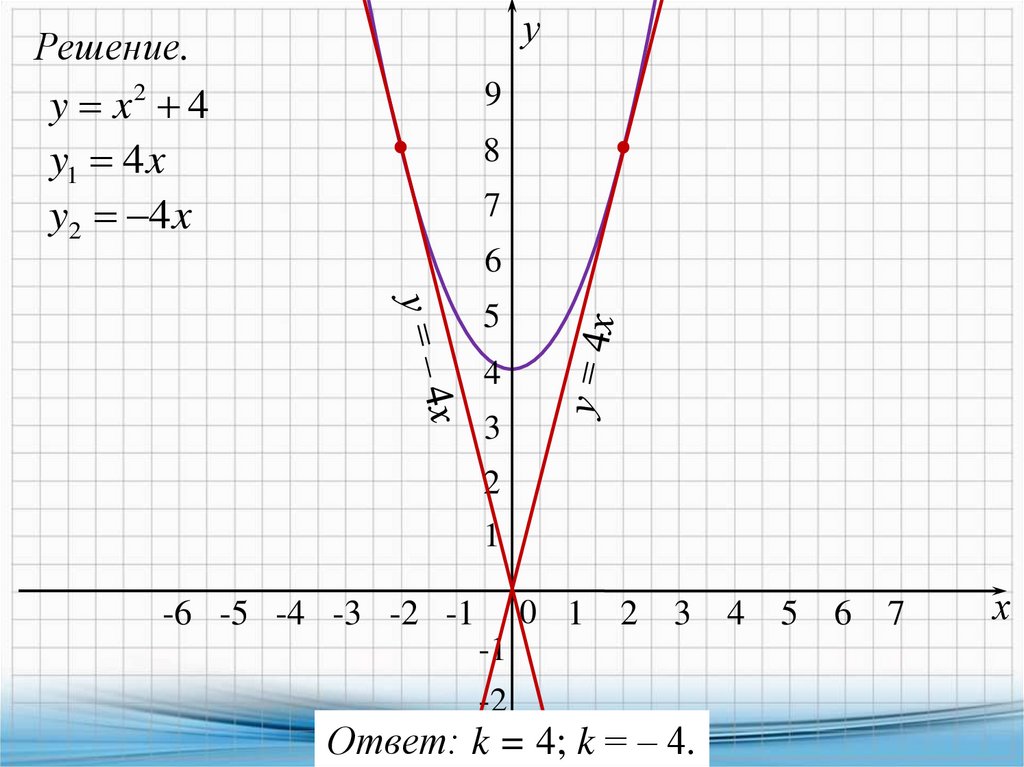
у
Решение.
2
y x 4
y1 4 x
y2 4x
9
8
7
6
5
4
3
2
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
-2
Ответ: k = 4; k = ‒ 4.
4
5
6
7
х

18.

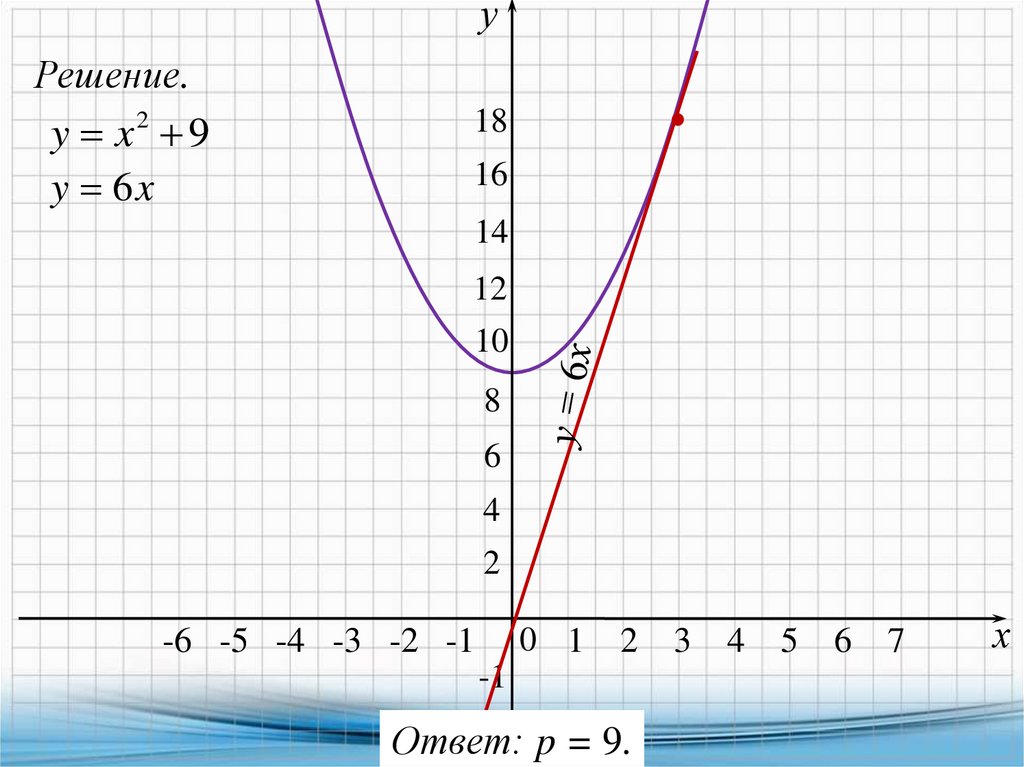
7. Найдите p и постройте график функции y = x2 + p если
известно, что прямая y = 6x имеет с этим графиком ровно одну
общую точку.
Решение.
Прямая y=6x имеет с графиком функции y = x2 + p ровно одну
общую точку, если уравнение 6 x x 2 p имеет один корень.
Такое возможно, когда дискриминант равен 0.
6x x2 p
x2 6x p 0
D 36 4 p
1 корень
D 0 36 4 p 0
p 9.

19.

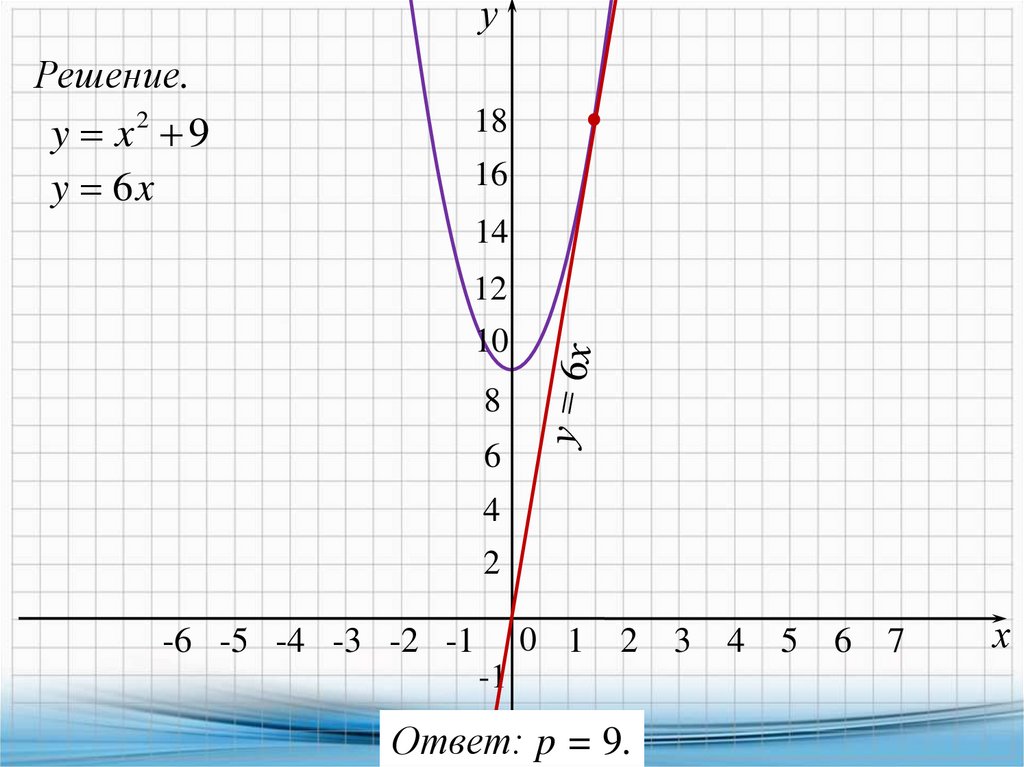
у
Решение.
y x2 9
y 6x
18
16
14
12
10
8
6
4
2
-6 -5 -4 -3 -2 -1
0 1
2
-1
-2 p = 9.
Ответ:
3
4
5
6
7
х

20.

у
Решение.
y x2 9
y 6x
18
16
14
12
10
8
6
4
2
-6 -5 -4 -3 -2 -1
0 1
2
-1
-2 p = 9.
Ответ:
3
4
5
6
7
х

21.

8. Постройте график функции
x
y
2
x x
x 1
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x2 x x
y
x 1
2
x
x 2 x x x x 1 x
, если х 0;
xx 2
x 1
x 1
х , если х 0.
при условии х 1 0
х 1.

22.

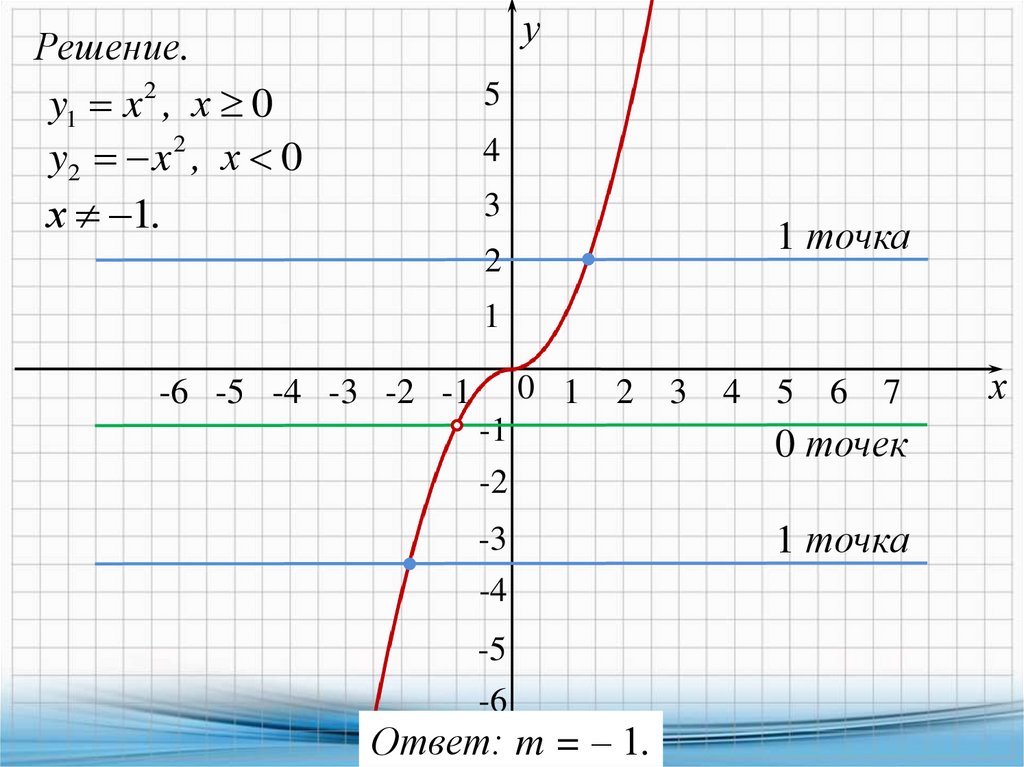
у
Решение.
y1 x 2 , х 0
2
y2 x , х 0
5
4
х 1.
3
1 точка
2
1
0 1
-6 -5 -4 -3 -2 -1
2
3
4
5
6
7
-1
-2
0 точек
-3
-4
1 точка
-5
-6
Ответ: m = ‒ 1.
х

23.

.