Similar presentations:
Бинарный поиск
1. Бинарный поиск
БИНАРНЫЙ ПОИСК2.
Двоичный поиск – это алгоритм свременной сложностью O(log n),
который например, позволяет
эффективно проверить, встречается ли
в массиве заданное значение.
3.
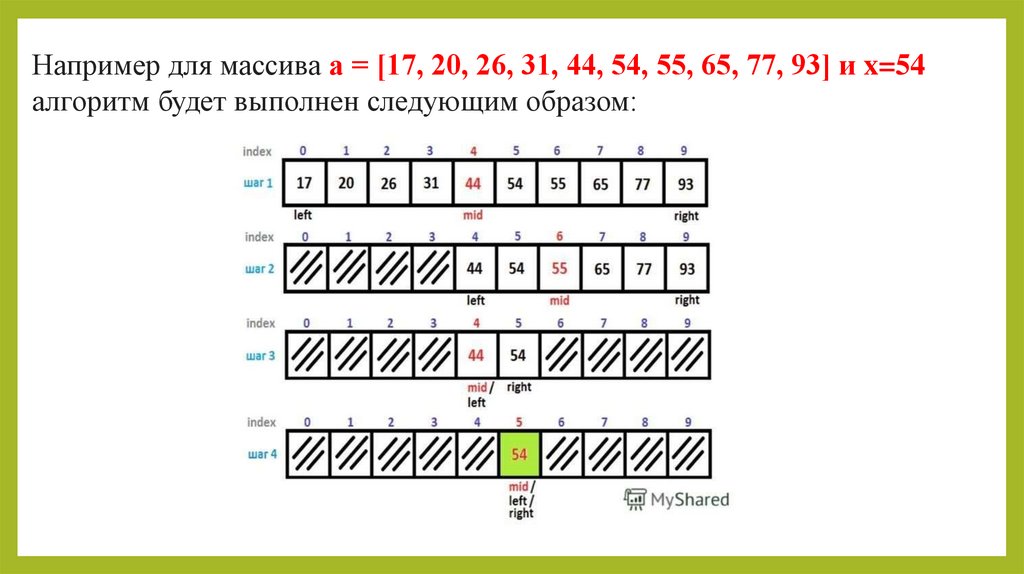
Реализация поискаПусть дан отсортированный массив с n элементами, и мы
хотим проверить, встречается ли в нем значение x.
Алгоритм состоит из ряда шагов, на каждом их которых
диапазон поиска делится пополам. На каждом шаге
проверяется средний элемент активного подмассива. Если
средний элемент совпадает с искомым значением , то поиск
заканчивается. В противном случае поиск рекурсивно
продолжается в левой или правой половине подмассива в
зависимости от значения среднего элемента.
4.
Например для массива a = [17, 20, 26, 31, 44, 54, 55, 65, 77, 93] и x=54алгоритм будет выполнен следующим образом:
5.
Давайте научимся решать следующую задачу — вотсортированном массиве нужно найти ближайший к
числу x элемент Нам же в таком случае нужно решить
следующие две задачи:
•Найти максимальный элемент, не больше
чем x (ближайший к x слева)
•Найти минимальный элемент, не меньше
чем x (ближайший к x справа)
6.
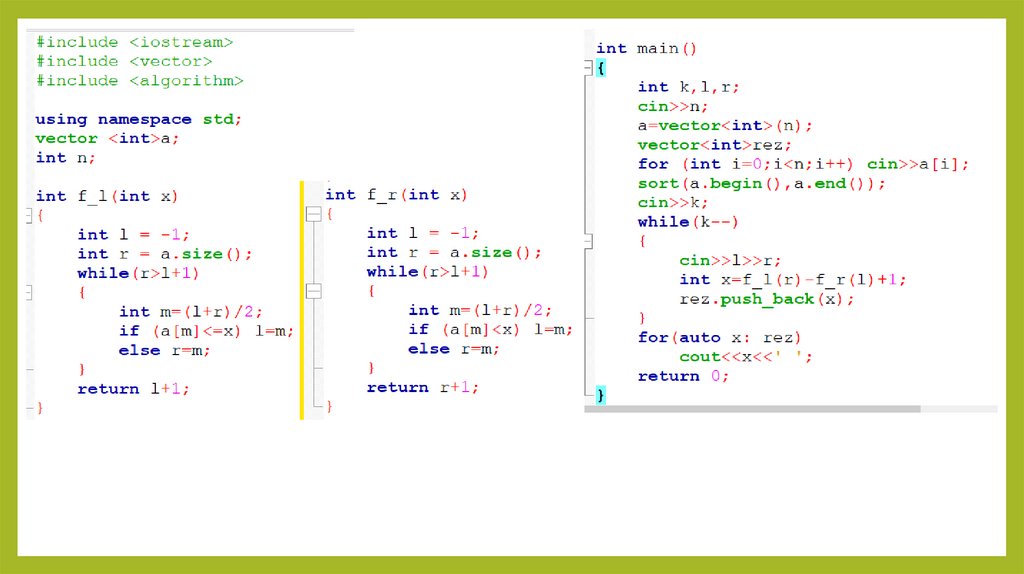
Рассмотрим алгоритм бинарного поиска для решения первой задачи(максимальный элемент, не больший x).
Нам задан массив a=[a0,a1,…,an−1]. Заведём два указателя l и r. Они будут
отвечать за границы рассматриваемого отрезка.
Чтобы al≤x, а ar>x выполнялось добавим в начало массива −∞ (индекс
этой бесконечности будет −1), а в конец массива +∞ (индекс этой
бесконечности будет n+1). Тогда поставим l в −1, а r в n.
Будем выполнять следующий алгоритм, пока l+1 < r (пока указатели не
сойдутся):
•Пусть m — индекс середины отрезка [l,r];
•Если am≤x, то положим l=m. Все элементы левее, чем m меньше, чем am;
•Если am>x, то положим r=m. Все элементы правее, чем m больше, чем am.
7.
Максимальный элемент, не больше чем x (ближайший к x слева)8.
Минимальный элемент, не меньше чем x (ближайший к x справа)9. Рассмотрим задачи https://acmp.ru/ курсы Язык программирования C++ темы Бинарный поиск
Рассмотрим задачиhttps://acmp.ru/
курсы
Язык программирования C++
темы Бинарный поиск
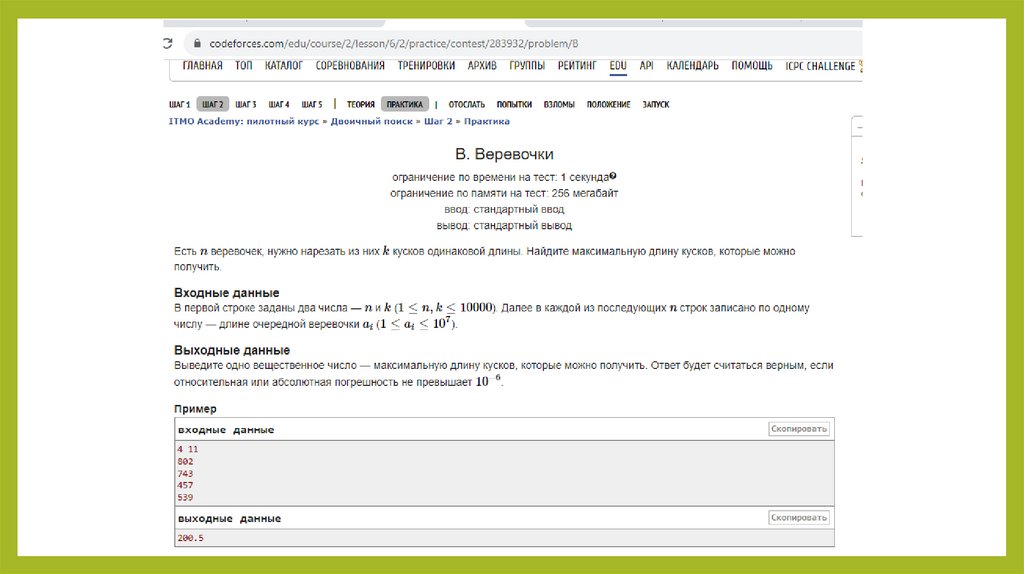
10. Рассмотрим задачи https://codeforces.com/edu/course/2
11.
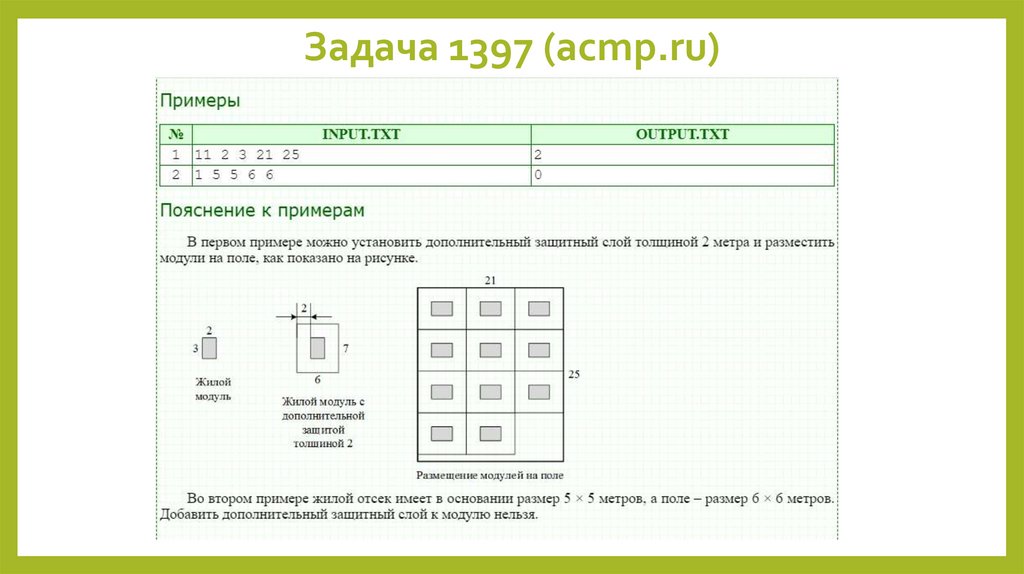
12. Задача 712 (acmp.ru)
Пример расстановки10 дипломов 2х3 в
квадрате 9х9:
13. Задача 712 (acmp.ru)
если в квадрат со стороной x можно поместить все прямоугольники,то в квадрат со стороной x+1 их тоже можно поместить,
так как квадрат стал больше.
Чтобы посчитать количество прямоугольников,
помещающихся в квадрат x×x, перемножим количество
прямоугольников, которые помещаются по первой
стороне - ⌊x/a⌋, и количество прямоугольников, которые
помещаются по второй стороне — ⌊x/b⌋.
Итоговая формула: ⌊xa⌋⋅⌊xb⌋.
14. Задача 712 (acmp.ru)
Минимальныйэлемент, не меньше
чем x (ближайший
x справа)
Чобы не было
переполнения в
(mid/w)*(mid/h)
Используем
(1.0*(mid/w)*(mid/h)<n)
15.
16.
17. Задача 267 (acmp.ru)
Левая граница l= 0 минПравая граница r = max(x,y)*n
Бинарный поиск по (m/x)+(m/y) <n
где m – средина
Минимальный элемент,
не меньше
чем x (ближайший x спр
ава)
18. Задача 267 (acmp.ru)
19.
20.
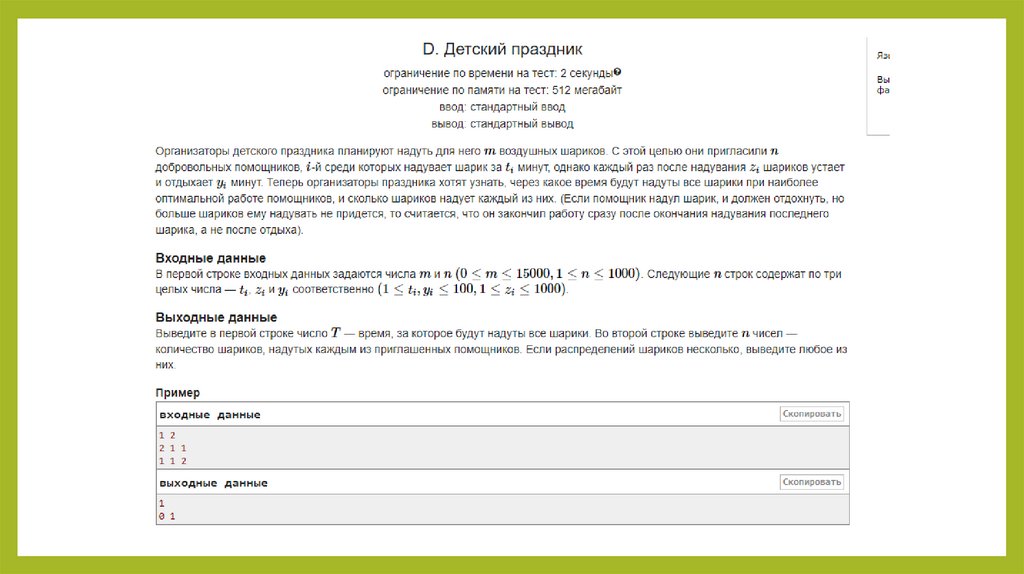
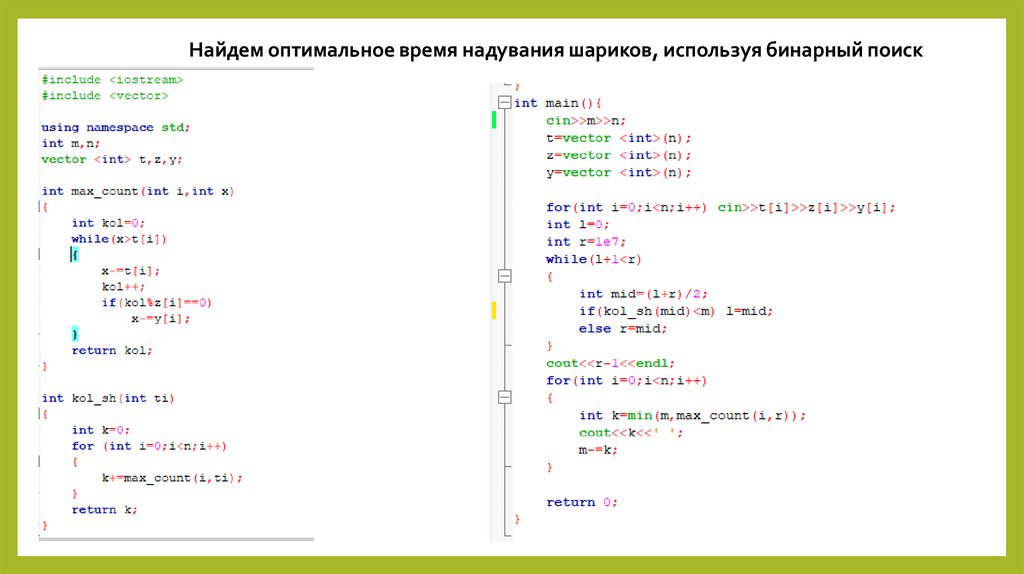
Найдем оптимальное время надувания шариков, используя бинарный поиск21.
22.
23. Задача 1030 (acmp.ru)
24. Задача 1030 (acmp.ru)
Максимальныйэлемент, не больше
чем x (ближайший
к x слева)























 informatics
informatics








