Similar presentations:
Метод конечных элементов
1.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«УФИМСКИЙ УНИВЕРСИТЕТ НАУКИ И ТЕХНОЛОГИЙ»
ФАКУЛЬТЕТ ФИЗИКИ И МАТЕМАТИКИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И ФИЗИКИ
КУРСОВАЯ РАБОТА
Тема: «Метод конечных элементов»
Научный руководитель:
Доцент, к.ф.-м.н.
Чудинов В.В
Выполнил студент: 3 курса,
очной формы обучения 1 группы
Шарафуллин И.Х
БИРСК, 2023
2.
АктуальностьМетод конечных элементов является одним из основных
инструментов инженерного анализа и проектирования. Понимание
принципов и применение метод конечных элементов в решении задач
механики деформируемого твердого тела имеет большое значение для
инженеров различных специальностей, таких как механика,
строительство, авиация, автомобилестроение и другие. Кроме того,
развитие методов численного анализа и использование МКЭ в
инженерной практике позволяет улучшить качество проектирования и
сократить затраты на испытания и моделирование физических
процессов. Таким образом, изучение метод конечных элементов имеет
большое значение для специалистов в области инженерии
3.
Цели работы• 1. Изучить основы Метода
конечных элементов.
• 2. Изучить применение
метода конечных
элементов в различных
областях.
• 3. Понять общий алгоритм
расчета
4.
Метод конечных элементовМетод конечных элементов - является численным методом решения дифференциальных
уравнений, встречающихся в физике и технике. Метод конечных элементов является одним из наиболее
широко применяемых численных методов в науке и инженерии. Он представляет собой мощный
инструмент для моделирования и анализа различных физических явлений и процессов. Метод конечных
элементов позволяет решать сложные задачи, которые не могут быть решены аналитически, и
предоставляет возможность получить информацию о поведении системы при различных условиях.
Основная идея метода конечных элементов заключается в разбиении сложной геометрии исследуемой
области на более простые подобласти, называемые конечными элементами.
5.
Важными преимуществами МКЭ1) Свойства материалов не должны быть обязательно одинаковыми.
Это позволяет применить метод к телам, составленным из
нескольких материалов
2) Криволинейная
область
может
быть
аппроксимирована
с
помощью прямолинейных конечных элементов (например, с
помощью треугольных, призматических, шестигранных конечных
элементов).
3) Размеры элементов могут быть переменными. Это позволяет
укрупнить или уменьшить сетку разбиения области на элементы,
если в этом есть необходимость
6.
Применение метода конечных элементов в различных областяхМКЭ также применяется в области электромагнетизма для моделирования и анализа электромагнитных полей и процессов.
В гидродинамике МКЭ используется для моделирования и анализа движения жидкостей и газов.
Метод конечных элементов (МКЭ) широко применяется в механике для анализа и моделирования поведения твердых тел и
структур
7.
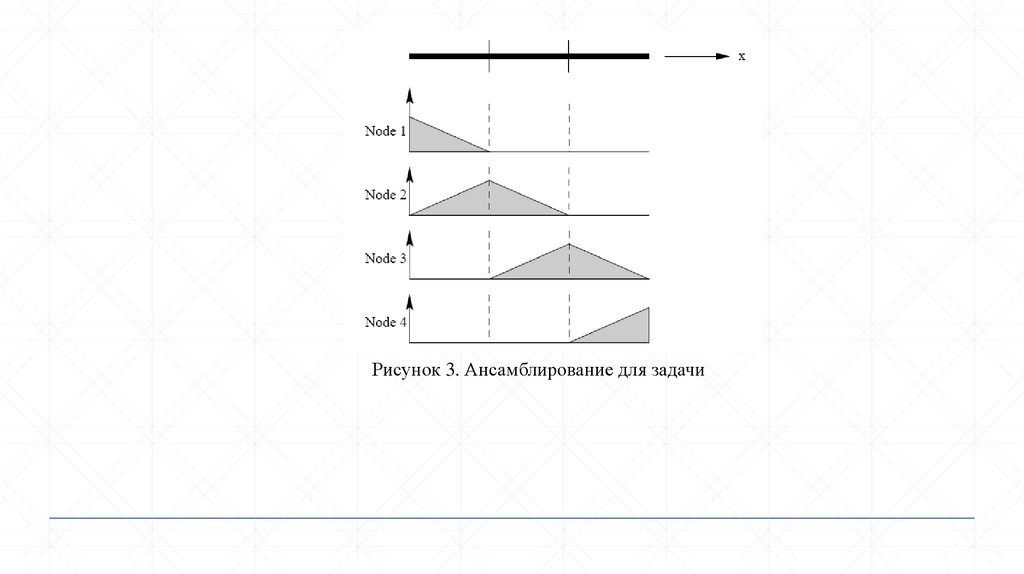
Общий алгоритм расчета МКЭ1. Дискретизация конструкции. Рассматриваемая область представляется в виде совокупности конечных
элементов, соединенных между собой в узловых точках
2. Построение глобальных матрицы жесткости и вектора узловых сил.
3. Учет заданных граничных условий.














 mathematics
mathematics physics
physics








