Геоморфометрия

1. Что такое геоморфометрия???

Геоморфометрия - это наука количественного анализа
формы земной поверхности (Pike, 1995, 2000a;
Rasemann et al., 2004)
Это современный, аналитико-картографический подход
к анализу рельефа как совокупности отметок высот с
использованием
вычислительной
техники.
(Tobler,1976,2000)

2. Синонимы

• моделирование рельефа\ terrain modeling(Li et al.,
2005),
• анализ рельефа \terrain analysis (Wilson and Gallant,
2000)
• наука о топографии\science of topography (Mark and
Smith, 2004)
• цифровое моделирование рельефа\ digital terrain
modeling (Pike, 2002).
Объектом изучения во всех выше перечисленных
случаях является земная поверхность\land surface

3. Параметры и объекты

• параметры земной поверхности\land surface
parameters (описывают форму земной
поверхности в определенной точке к ним
можно отнести угол наклона, экспозицию,
кривизы земной поверхности и т.д. );
• объекты земной поверхности\land-surface
objects (обособленные пространственные
объекты, такие как границы водосборных
бассейнов, сеть водотоков, ландшафтные
единицы и т.д. ).

4.

• z = f(x, у) + e1 + e2
• где f(x, у) - детерминистический
компонент, который может быть описан
с использованием какой-нибудь
функции;
• e1 – систематическая ошибка;
• e2 – случайная ошибка
• Проблема: очень трудно подобрать уравнение,
которое бы с приемлемыми ошибками
описывало более менее крупную территорию!!

5.

• DEM –digital elevation model(цифровые
модели высот:
• DTM - digital terrain model (цифровые
модели рельефа ЦМР);
• DSM - digital surface model (цифровые
модели местности;

6.

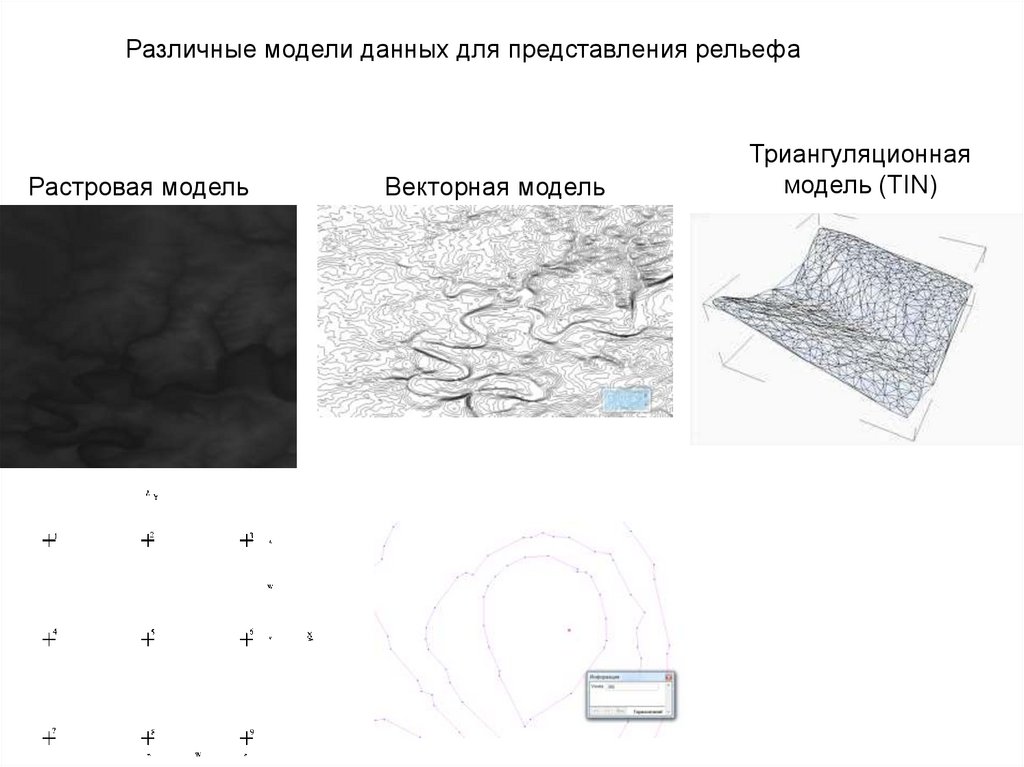
Различные модели данных для представления рельефа
Растровая модель
Векторная модель
Триангуляционная
модель (TIN)

7.

Преимущества ЦМВ:
• ЦМВ имеют простую структуру и могут быть легко перестроены;
Сравнительно более легкое получение параметров и объектов земной
поверхности в силу использования более простых алгоритмов;
• Имеют унифицированную пространственную структуру, почти все
свойства таких ЦМВ определяются размером ячейки ЦМВ;
Больше подходит для задач отображения и вывода на печать.
Недостатки ЦМВ:
• Для отображения территорий со сложным рельефом необходимо
хранение большего количества данных, чем с использованием
альтернативных моделях для достижения одинаковой точности;
• Смена проекций растровых ЦМВ происходит медленнее и ведет к потере
точности. Это происходит из-за того, что исходная регулярная структура
перестает быть таковой в новой проекции и она должна быть
пересчитана;

8.

Свойства растровой модели данных
Разрешение и шаг
Минимальная линейная
размерность
наименьшей
единицы
географического пространства, для которой могут быть приведены
какие-либо данные
В растровой модели данных наименьшей единицей для большинства
систем выступает квадрат или прямоугольник. Такие единицы известны
как сетка, ячейка или пиксель. Множество ячеек образует решетку,
растр, матрицу.
Значение
Единица информации, хранящаяся в слое для каждого пикселя или
ячейки. Ячейки одной зоны (или района) имеют одинаковое значение
Местоположение
Наименьшая единица географического пространства, для которого
могут быть приведены какие-либо характеристики или свойства
(пиксель, ячейка)
Такая частица картографического плана однозначно идентифицируется
упорядоченной парой координат - номерами строки и столбца
Размер матрицы(растра) – количество столбцов и колонок, которые
образуют матрицу.

9. Основные этапы геоморфометрического анализа

• Измерение отметок высот земной поверхности с
использованием того или иного метода;
• создание модели земной поверхности на основе
данных измерений;
• оценка ошибок полученной модели и их
исправление;
• получение параметров и/или объектов земной
поверхности;
• применение полученных характеристик и объектов
земной поверхности для каких либо исследований и
задач (географических, геоэкологических,
экологических, кадастровых и т.п.).

10.

11.

12.

13.

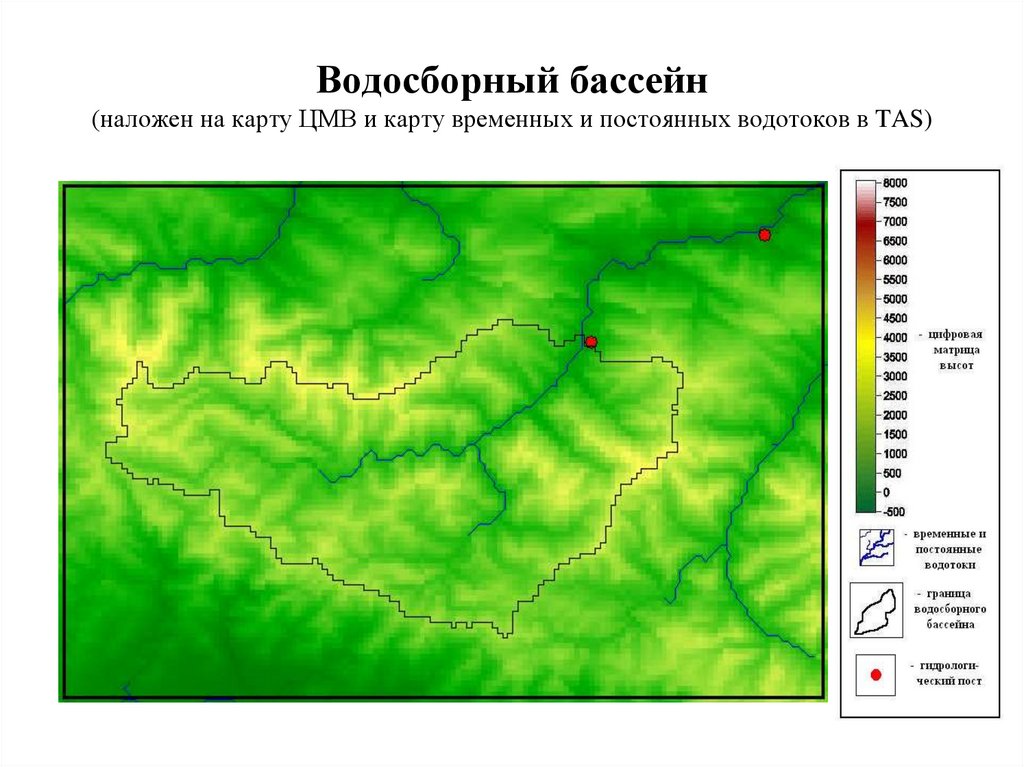
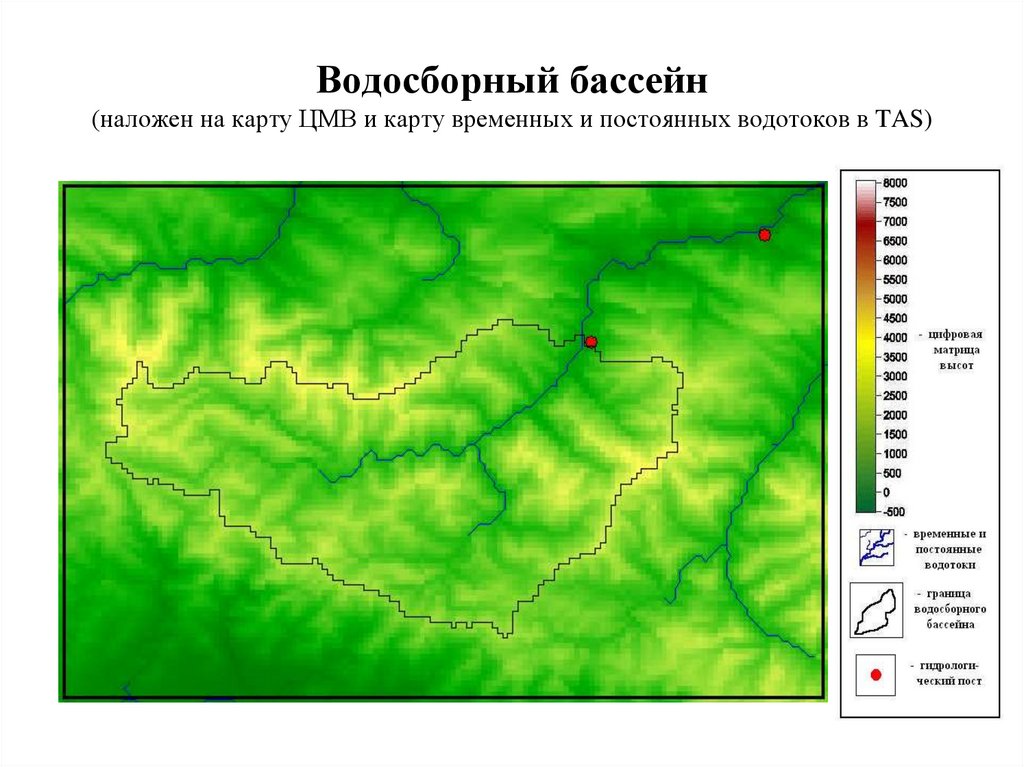
14. Водосборный бассейн (наложен на карту ЦМВ и карту временных и постоянных водотоков в TAS)

15. Глобальные модели рельефа в открытом доступе

• ETOPO5 разрешение 5’ – это около 5 км.;
• GTOPO30 разрешение 30’’ – это около 900 м.;
• GMTED 2010 – Global Multi-resolution Terrain Elevation
Data 2010.
• SRTM - Shuttle radar topographic mission;
• Aster(advanced spaceborne thermal emission and reflection
radiometer) GDEM(global digital elevation model);
• AW3D30 DSM v.1.1 –«ALOS(Advanced Land Observing
Satellite) World 3D-30m.

16.

GMTED 2010
Шаг сетки: 7.5’’, 15’’, 30’’- это около - 250,500,1000 м.
Источники данных: модель была создана с использованием 11-ти
различных источников данных о рельефе Земли, в том числе
SRTM для территорий южнее 60 с.ш., а также цифровых данных о
высотах, полученных с использованием стерео фотоснимков и
фотограмметрии при разрешении 100 м для территорий севернее
60 с.ш.
Проекция, эллипсоид: долгота/ широта на WGS 84;
Разработчик: U.S. Geological Survey (USGS) and the National
Geospatial-Intelligence Agency (NGA);
Доступна
для
скачивания:
https://topotools.cr.usgs.gov/gmted_viewer/gmted2010_global_grids.p
hp
Покрытие: 84 с.ш. - 56 ю.ш.
Особенности: для каждого разрешения существует несколько
вариантов моделей GMTED2010, которые отличаются алгоритмами

17.

SRTM
Шаг сетки: 1’’,3’’,30’’ - это около 30,90,900 м.
Источники данных: С 11 по 22 февраля 2000 года с борта
космического челнока «Индевор» были получены данные с
использованием двух радарных систем С-SIR и X-SAR, которые в
процессе последующей постобработки позволили получить
различные модификации глобальных общедоступных ЦМР.
Проекция, эллипсоид: долгота/ широта на WGS 84;
Разработчик:
космические
Германии(DLR) и Италии.
агентства
США(NASA,
USGA),
Доступна для скачивания:
SRTM C-SIR - https://lta.cr.usgs.gov/get_data/
SRTM Х-SAR- http://www.dlr.de/eoc/en/desktopdefault.aspx/tabid5515/9214_read-17716/
Покрытие: 60 с.ш. - 56 ю.ш.
Особенности: - - -

18.

19. Рельеф среднего Поволжья (данные SRTM3)

20.

ASTER GDEM v.3
Шаг сетки: 1’’ - это около 30 м.
Источники
данных:
усовершенствованный
спутниковый
радиометр теплового излучения и отражения установленный на
спутнике «Terra».
Проекция, эллипсоид: долгота/ широта на WGS 84;
Разработчик: Старт миссии ASTER был
дан при участии
Министерства экономики, торговли и промышленности Японии и
Национального аэрокосмического агентства США в 1998 году.
Доступна для скачивания:https://search.earthdata.nasa.gov/search
Покрытие: 83 с.ш. - 83 ю.ш.
Особенности: - - -

21.

AW3D30 DSM v.1.1
Шаг сетки: 1’’ - это около 30 м.
Источники данных: создан на основе коммерческого набора
данных «World 3D Topographic Data» за счет уменьшения его
горизонтального разрешения. Модель рельефа «World 3D
Topographic Data» была создана на основе данных, полученных со
спутника ALOS(Advanced Land Observing Satellite) «DAICHI».
Проекция, эллипсоид: долгота/ широта на WGS 84;
Разработчик: японское агентство аэрокосмических исследований
(Japan Aerospace Exploration Agency - JAXA)
Доступна для скачивания: https://lta.cr.usgs.gov/get_data/
Покрытие: 82 с.ш. - 82 ю.ш.
Особенности: - - -

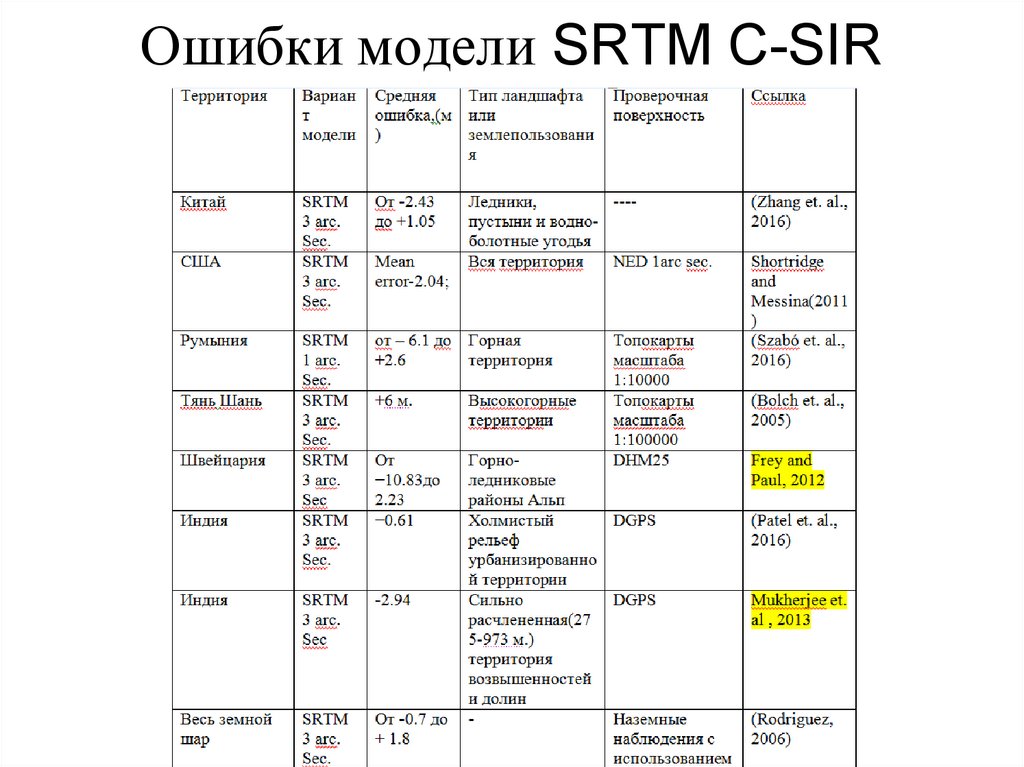
22. Ошибки модели SRTM C-SIR

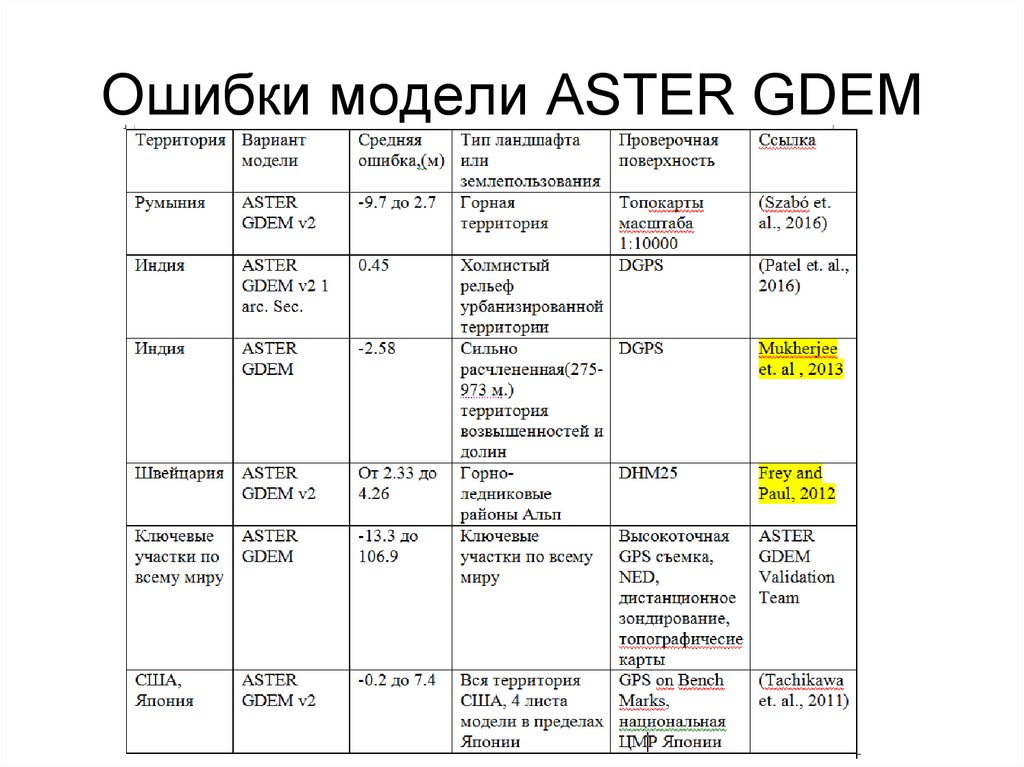
23. Ошибки модели ASTER GDEM

24. Источники данных для самостоятельного создания ЦМР

• Тематическая информация о рельефе
оцифрованная с топографических карт;
• Данные дистанционного зондирования
(аэрофотостереосъемка; радарная
съемка; LIDAR съемка);
• Данные наземной съемки имеющих
геодезическую точность;

25. Данные наземной съемки имеющих геодезическую точность

• Оборудование:
обычный
тахеометр,
роботизированный
тахеометр,
высокоточный(как правило двух частотных)
прибор позиционирования станции съемки
тахеометром, привязка к базовым станциям.
• Программное обеспечение: позволяющее
выполнить пространственную интерполяцию.
• Данные:
список
триплет
координат
расположенных нерегулярно (Surfer, CREDO).
• Плюсы: высокая точность, гибкость – точность измерений
может изменяться в зависимости от типа земной поверхности,
требуется относительно небольшой объем камеральной
обработки следующих за измерениями;
• Минусы: необходимость в дорогом оборудовании; большое
количество усилий и времени необходимых для съемки.

26. Набор точек с высотами представляющих результат наземной геодезической съемки.

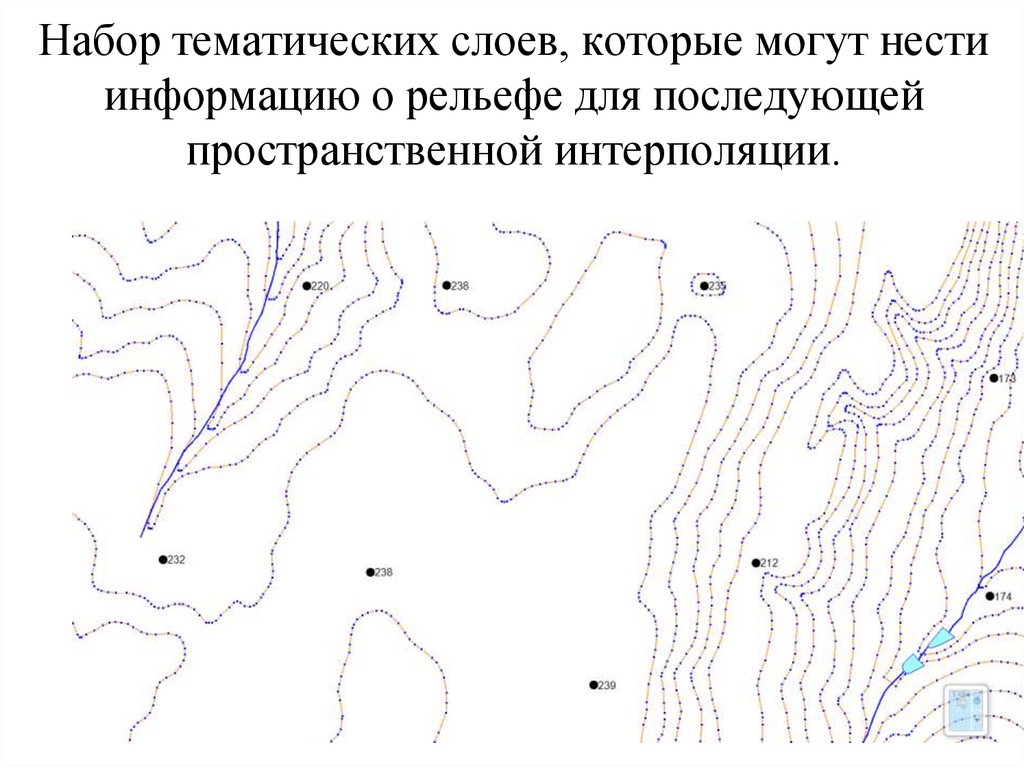
27. Тематическая информация о рельефе оцифрованная с топографических карт;

• Оборудование:
сканер
или
дигитайзер,
персональный
компьютер.
• Программное
обеспечение:
позволяющее
выполнить
пространственную
интерполяцию
по
набору
тематических
слоев(ArcGIS).
• Данные:
в
виде
набора
тематических
слоев(горизонтали,
отметки высот, реки, озера, обрывы
овраги)
• Плюсы: низкая стоимость как оборудования так и программного
обеспечения; относительно быстрый способ получения ЦМР;
возможность
получать
точные
модели
при
наличии
высокоточных карт.
• Минусы: доступ к картам ограничен.

28. Набор тематических слоев, которые могут нести информацию о рельефе для последующей пространственной интерполяции.

29. Данные дистанционного зондирования (аэрофотостереосъемка);

• Оборудование: летательный аппарат с
фотокамерой, высокоточный(как правило
двух частотных) прибор позиционирования
точек привязки.
• Программное обеспечение: позволяющее
выполнить фотограмметрию (PhotoScan),
БПЛА DJI Phantom 4
позволяющее выполнить пространственную
• Камера 12mpx
• Максимальное расстояние
интерполяцию (Surfer).
полета 6000м
• Данные: набор стереофотоснимков, список
• Максимальная высота
триплет
координат
расположенных
полета 500м
нерегулярно.
• Плюсы: скорость – быстрое покрытие относительно больших
территорий.
• Минусы: относительная дороговизна оборудования, систематическая
ошибка обусловленная искажениями которые дает камера, качество
получаемой модели зависит от погодных условий(облачность или
туман), времени суток(ночь), растительности, снежного покрова,
застройки территории, наличие точек привязки.

30.

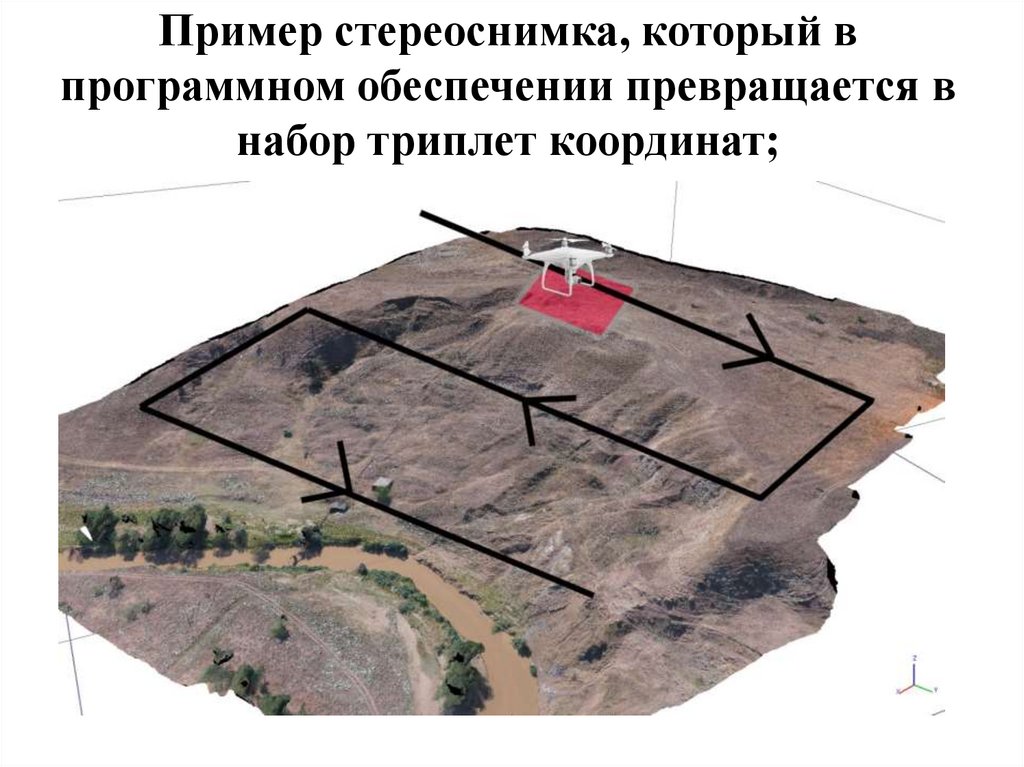
Пример стереоснимка, который в
программном обеспечении превращается в
набор триплет координат;

31.

Данные дистанционного зондирования
(LIDAR съемка)
• Оборудование: летательный аппарат с лазерным радаром,
высокоточный(как правило двух частотных) встроенный прибор
позиционирования летательного аппарата.
• Программное
обеспечение:
позволяющее
пространственную интерполяцию (Surfer).
• Данные:
список
нерегулярно.
триплет
координат
выполнить
расположенных
• Плюсы: скорость – быстрое покрытие относительно больших
территорий,
большая
точность
по
сравнению
со
стереофотосъемкой, множественность сигнала.
• Минусы: относительная дороговизна оборудования, качество
получаемой модели зависит от, плотности растительности,
снежного покрова, застройки территории, условий рельефа.

32.

Данные дистанционного зондирования
(RADAR съемка)
• Оборудование:
летательный
аппарат
воздушного
или
космического базирования, высокоточный(как правило двух
частотных) встроенный прибор позиционирования летательного
аппарата, съемочная аппаратура выполняющая съемку в
длинноволновом диапазоне электромагнитного спектра волн (35 см).
• Программное
обеспечение:
позволяющее
выполнить
интерферометрию(процесс создания ЦМР на основе данных с
радаров.
• Данные: данные либо с двух радаров, либо с одного радара но
выполнившего съемку исследуемой территории дважды.
• Плюсы: самая высокая скорость и охват съемки, независимость
от погодных условий, времени суток.
• Минусы: самое дорогое оборудование по сравнению с выше
приведенным, самая низкая точность по сравнению со всеми
выше приведенными методами, постобработка радарных
снимков процесс намного более сложный чем постобработка во
всех выше перечисленных методах.

33.

• EDM - Electronic Distance Measuring
технологии измеряющие
характеристики объектов с
использованием лазеров на расстоянии
(LASER /- Light Amplification by the
Stimulated Emission of Radiation)

34. Математические методы восстановления поверхностей

• Kriging
• Inverse Distance to Power
• Triangulation with Linear Interpolation
• Minimum Curvature
• Radial Basic Function
• Local Polinomial
• Nearest neighbor

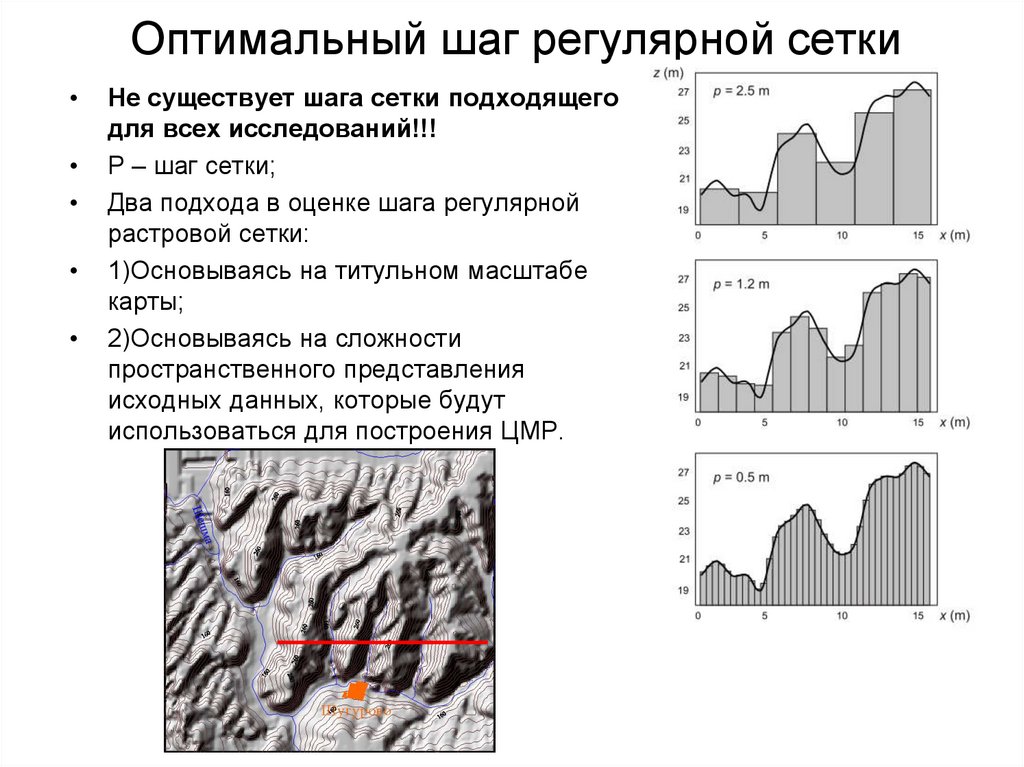
35. Оптимальный шаг регулярной сетки

Не существует шага сетки подходящего
для всех исследований!!!
Р – шаг сетки;
Два подхода в оценке шага регулярной
растровой сетки:
1)Основываясь на титульном масштабе
карты;
2)Основываясь на сложности
пространственного представления
исходных данных, которые будут
использоваться для построения ЦМР.

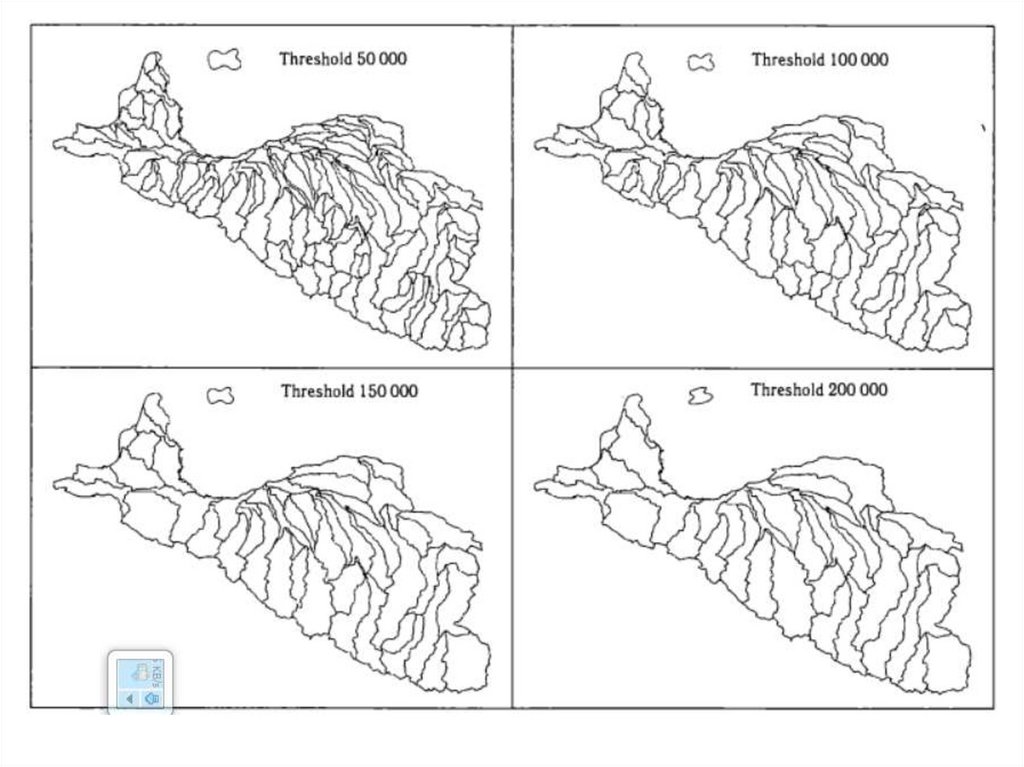
36.

1)Основываясь на титульном масштабе карты:
Например. Если мы в качестве исходных данных используем бумажные
топографические карты масштаба 1:50 000, то шаг сетки будет 25 метров, если
мы используем масштаб 1: 200 000, то шаг сетки будет 100 метров.
Как мы получаем такой шаг регулярной сетки?
Здесь важно знать с какой точностью были изготовлены исходные карты.
В случае с топокартами точно известно, что ошибка планового положения на них
составляет 0.5 мм. для равнин и 0.7 мм. для горной местности. В случае с
Республикой Татарстан это величина равна 0.5 мм. Полмиллиметра на карте
масштаба 1:50 000 – это 25 метров на местности.
То есть погрешность топографических карт масштаба 1:50 000 составляем
примерно 25 метров!!!

37.

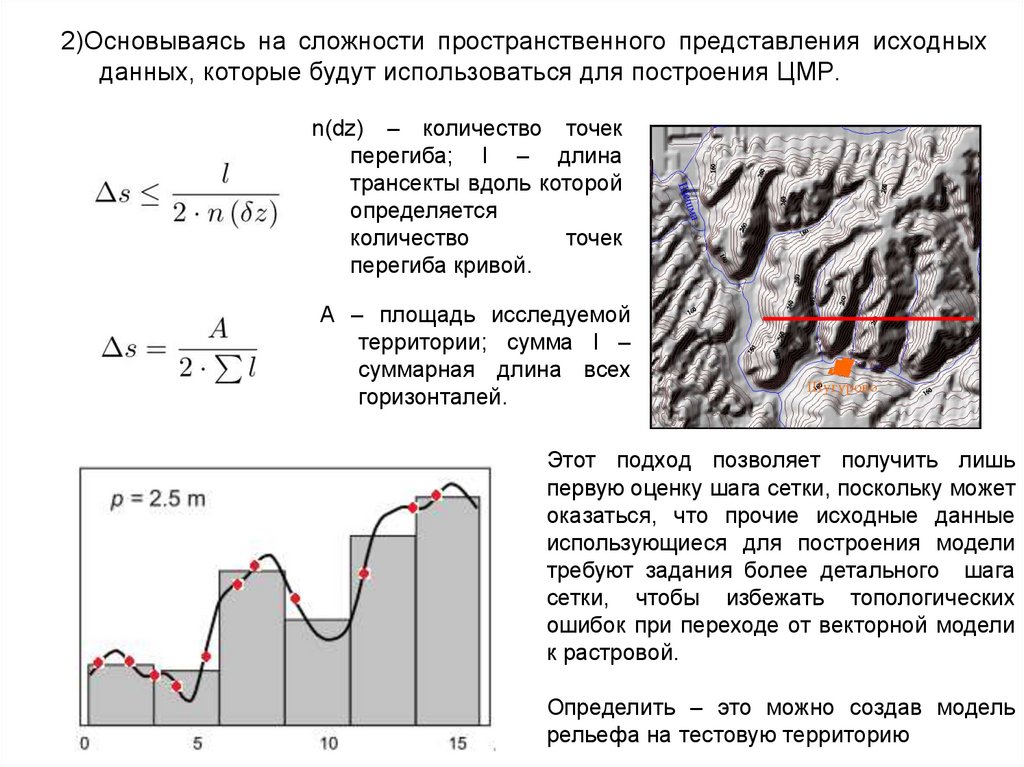
2)Основываясь на сложности пространственного представления исходных
данных, которые будут использоваться для построения ЦМР.
n(dz) – количество точек
перегиба; l – длина
трансекты вдоль которой
определяется
количество
точек
перегиба кривой.
А – площадь исследуемой
территории; сумма l –
суммарная длина всех
горизонталей.
Этот подход позволяет получить лишь
первую оценку шага сетки, поскольку может
оказаться, что прочие исходные данные
использующиеся для построения модели
требуют задания более детального шага
сетки, чтобы избежать топологических
ошибок при переходе от векторной модели
к растровой.
Определить – это можно создав модель
рельефа на тестовую территорию

38. Точные и сглаживающие интерполяторы

Все методы интерполяции можно разделить на точные и
сглаживающие интерполяторы.
Точные интерполяторы в точке выборки дают оценку, равную
измеренному в ней значению.
Оценка методами сглаживающей интерполяции, вычисленная в точке
выборки, не совпадает с измеренным в ней значением,
где Zi – значение высоты в узле регулярной сетки(черные точки),
- значение высоты в исходной точке(красные точки)
• Некоторые точные интерполяторы
имеют дополнительный параметр,
называемый
параметром
сглаживания, использование которого
превращает их в сглаживающие
интерполяторы.

39. Окрестность поиска

Методы интерполяции могут работать как глобальные и как локальные
интерполяторы. Глобальные интерполяторы вычисляют оцениваемые значения
на основе всего набора данных. Локальные интерполяторы использует
исходные данные лишь из некой локальной окрестности интерполируемой
точки, которая является меньшей пространственной областью внутри большей
изучаемой территории.
На настоящий момент различают три стратегии задания локальной
окрестности:
1) задание поискового эллипса;
2)задание определенного
регулярной сетки;
количества
точек
ближайших
к
узлу
3)на основе различных схем разбиения исследуемого пространства с
использованием сочленяющихся геометрических фигур ( например:
треугольники, полигоны)

40. Разные стратегии при поиске точек для интерполяции

У узлов регулярной сетки одинаковый
радиус поиска, но разное количество
точек для интерполяции, так для T1 –
17, a для Т2 – 24 точки.
В тоже время для узлов регулярной
сетки T3 и T4 количество точек
одиноково=5, но расстояния до этих
точек могут очень сильно различаться.

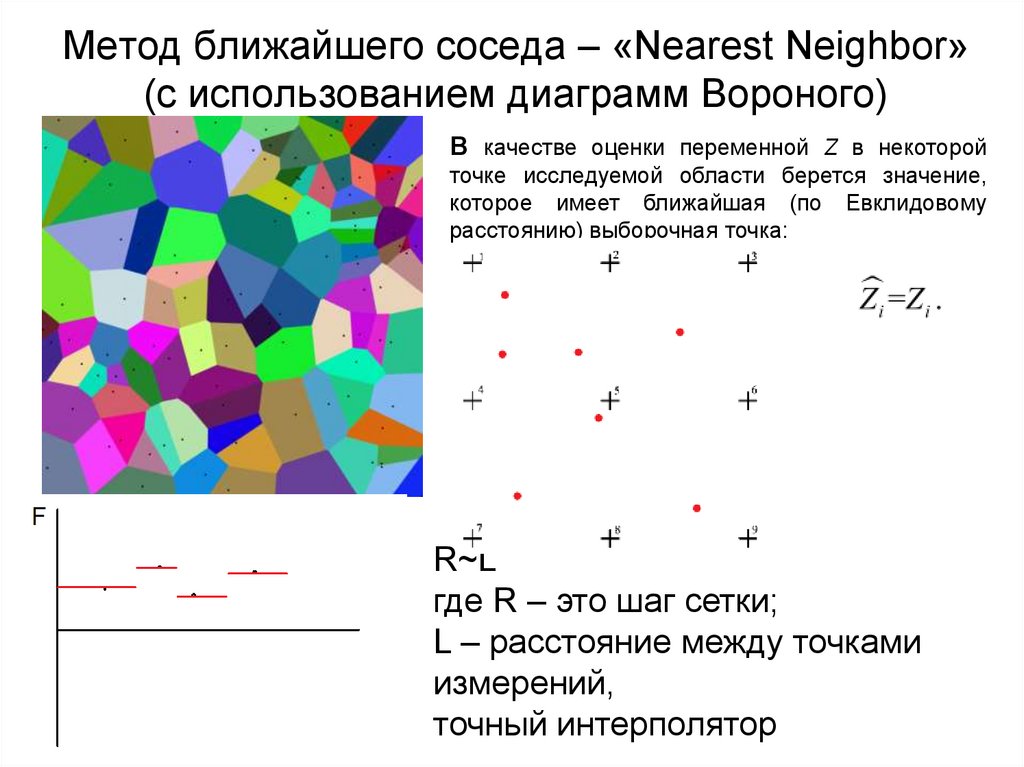
41. Метод ближайшего соседа – «Nearest Neighbor» (с использованием диаграмм Вороного)

В качестве оценки переменной Z в некоторой
точке исследуемой области берется значение,
которое имеет ближайшая (по Евклидовому
расстоянию) выборочная точка:
R~L
где R – это шаг сетки;
L – расстояние между точками
измерений,
точный интерполятор

42. Построенная поверхность методом ближайшего соседа (Surfer – метод аналитической отмывки)

43. Метод естественной окрестности – «Natural Neighbor»

В этом методе оценка переменной Z в некоторой точке области исследования
определяется как среднее взвешенное значений этой переменной в выборочных
точках (фактически в ближайших выборочных точках):
где веса wi0 определяются с использованием
диаграмм Вороного
• метод является точным интерполятором

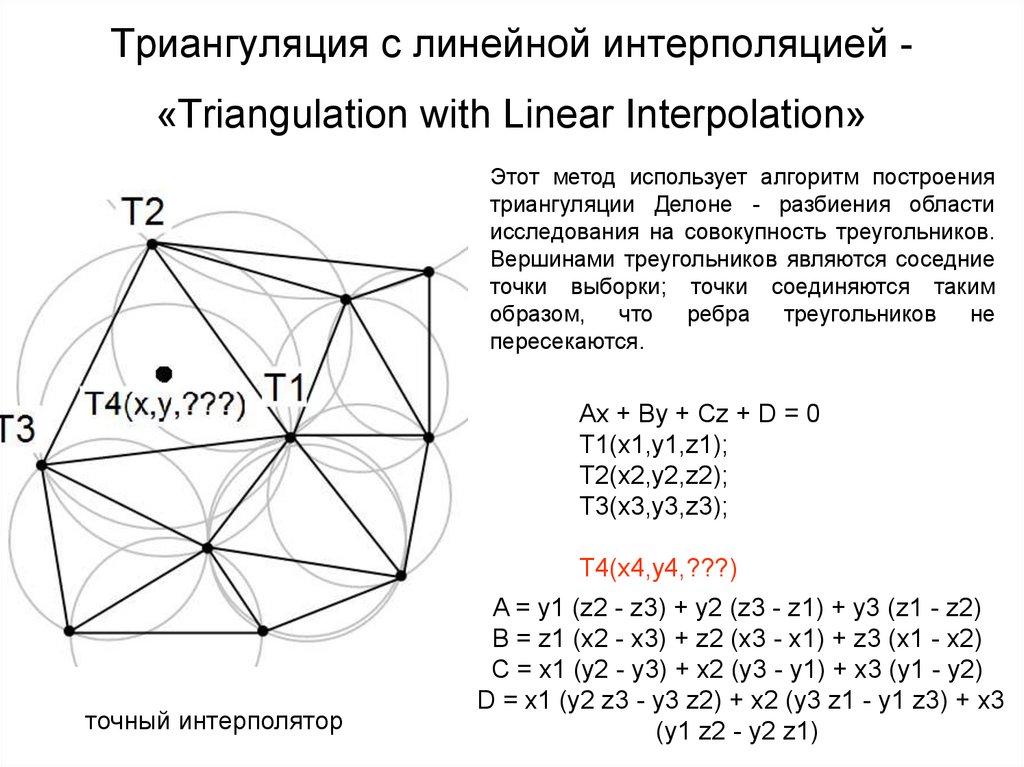
44. Триангуляция с линейной интерполяцией - «Triangulation with Linear Interpolation»

Триангуляция с линейной интерполяцией «Triangulation with Linear Interpolation»
Этот метод использует алгоритм построения
триангуляции Делоне - разбиения области
исследования на совокупность треугольников.
Вершинами треугольников являются соседние
точки выборки; точки соединяются таким
образом, что ребра треугольников не
пересекаются.
Ax + By + Cz + D = 0
T1(x1,y1,z1);
T2(x2,y2,z2);
T3(x3,y3,z3);
T4(x4,y4,???)
точный интерполятор
A = y1 (z2 - z3) + y2 (z3 - z1) + y3 (z1 - z2)
B = z1 (x2 - x3) + z2 (x3 - x1) + z3 (x1 - x2)
C = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)
D = x1 (y2 z3 - y3 z2) + x2 (y3 z1 - y1 z3) + x3
(y1 z2 - y2 z1)

45. Построенная поверхность методом Триангуляции с линейной интерполяцией (Surfer – метод аналитической отмывки)

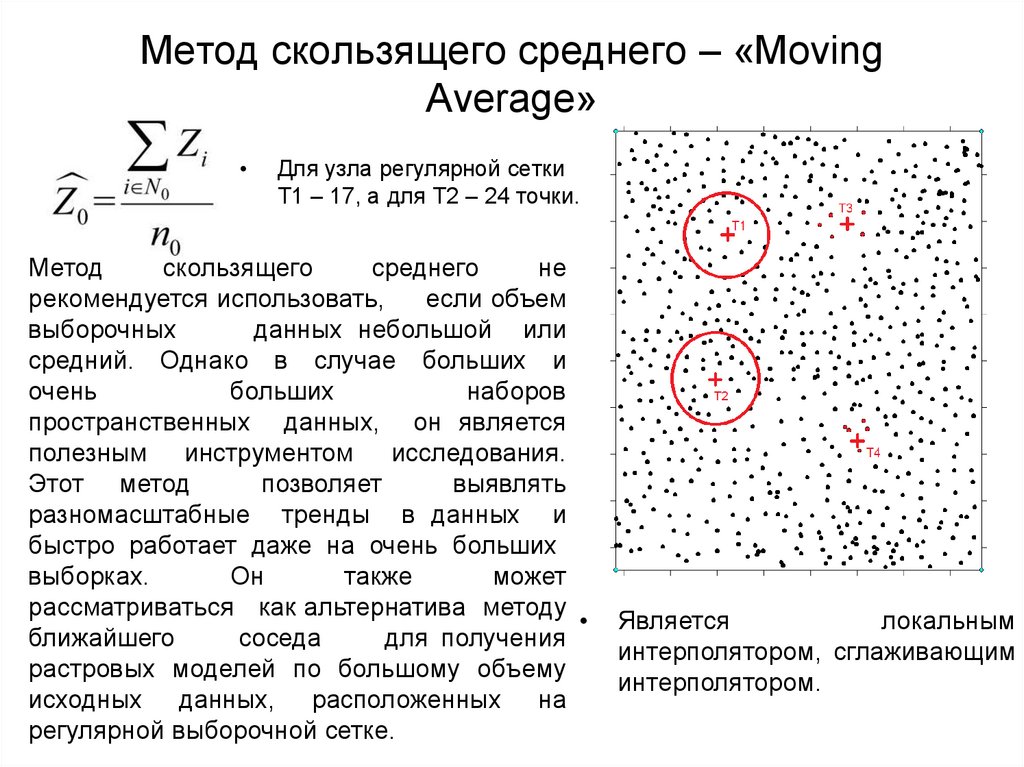
46. Метод скользящего среднего – «Moving Average»

Для узла регулярной сетки
T1 – 17, a для Т2 – 24 точки.
Метод
скользящего
среднего
не
рекомендуется использовать,
если объем
выборочных
данных небольшой или
средний. Однако в случае больших и
очень
больших
наборов
пространственных данных, он является
полезным инструментом исследования.
Этот метод
позволяет
выявлять
разномасштабные тренды в данных и
быстро работает даже на очень больших
выборках.
Он
также
может
рассматриваться как альтернатива методу
ближайшего
соседа
для получения
растровых моделей по большому объему
исходных данных, расположенных на
регулярной выборочной сетке.
Является
локальным
интерполятором, сглаживающим
интерполятором.

47. Обратно-взвешенные расстояния - «Inverse Distance to a Power»

N
• Z=
w Z
i 1
n
i0
w
i0
i 1
wi 0
i
1
( d )
2
i0
2
• где wi0 – эффективная разделяющая дистанция между 0-ым
узлом регулярной сетки и i точкой измерения; di0 – расстояние
между 0-ым узлом регулярной сетки и i точкой измерения; δ –
сглаживающий фактор; β – степенной взвешивающий параметр.
Если δ = 0, то метод работает как точный интерполятор

48. Построенная поверхность методом обратно пропорционально расстоянию (изменение параметров поиска точек для интерполяции)

Используется часть данных, при
радиусе поиска 400 м
Из-за недостаточности радиуса
поиска появляются области с
незаданными значениями
Используется часть данных, при
радиусе поиска 12,3 км
Областей с незаданными
значениями нет, общая картина
становится более гладкой,
(красным цветом помечены места
неправильно заданых отметок
высот при вводе исходных
данных)
Используются все данные для
расчета каждого узла сетки,
глобальный интерполятор
Областей с незаданными
значениями нет, общая картина
становится очень гладкой

49. Построенная поверхность методом обратно пропорционально расстоянию (изменение сглаживающего фактора)

Сглаживающий фактор =0
Сглаживающий фактор =100 Сглаживающий фактор =300
По мере увеличения сглаживающего фактора, происходит
сглаживание поверхности с появлением ортогональных структур

50. Построенная поверхность методом обратно пропорционально расстоянию (изменение показателя степени)

Степень =2
Степень =1
Степень =0.1
По мере уменьшения степени идет сглаживание рельефа,
с появлением ортогональных структур

51. Использованием сплайн интерполяции с применением метода минимальной кривизны - «Minimum Curvature»

Использованием сплайн интерполяции с
применением метода минимальной кривизны «Minimum Curvature»
1) Аппроксимация исходных точек с использованием AX+BY+C=Z(X,Y)
(точек как правило больше, чем нужно для определения параметров);
2) Оценка ошибок между результатами моделирования и наблюденными
значениями;
3) Использование алгоритма минимальной кривизны для моделирования
ошибки;
(1 Ti ) 2 ( 2 Z ) (Ti ) 2 Z 0
2Z
Z
(1 Tb ) 2 (Tb )
0
n
n
2Z
0
x y
где 2 - оператор Лапласа,
n – нормаль к границе,
Ti – внутреннее натяжение используемое
для всех основных узлов сетки,
Tb – натяжение на границе
Метод не является точным интерполятором
4)Сложение двух регулярных сеток, результатов моделирования полиномом
(этап1) и моделирования ошибки (этап3).

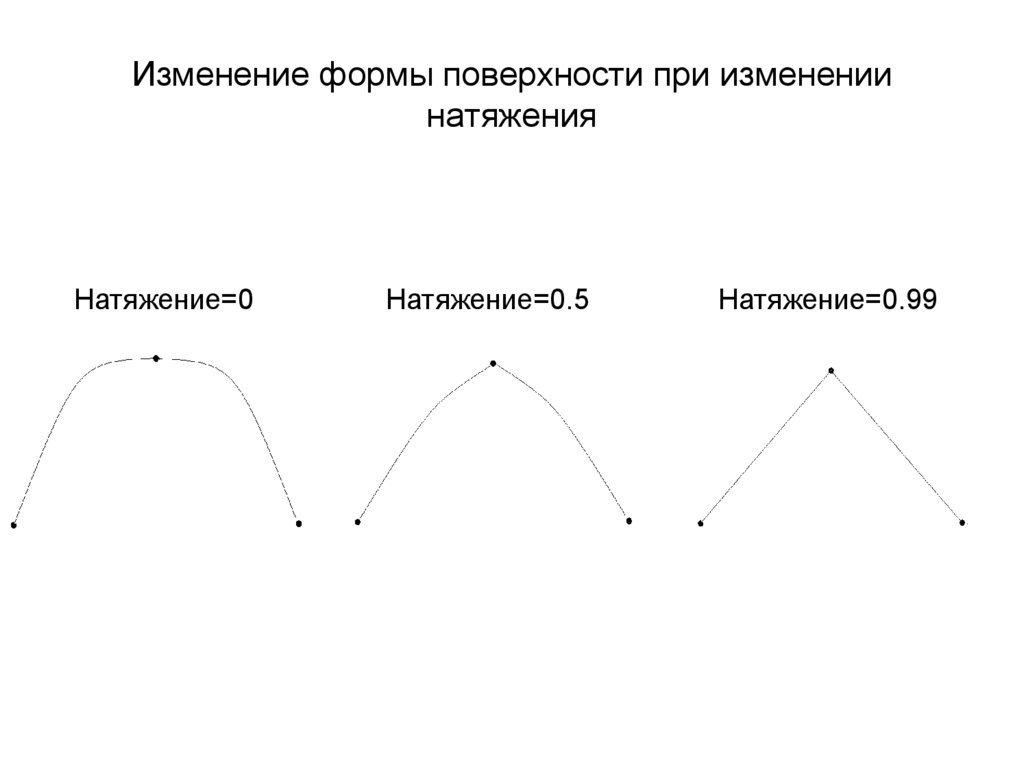
52. Изменение формы поверхности при изменении натяжения

Натяжение=0
Натяжение=0.5
Натяжение=0.99

53. Параметры алгоритма

• Внутреннее натяжение Ti/Internal tension;
• Натяжение на границе Tb/Boundary Tension;
• Количество итераций/Number of iteration –
количество повторений выполнения этапов(14);
• Фактор расслабления/Relaxation factor;
• Максимальная разница(ошибка)/Maximum
residual;

54.

Натяжение=0
Натяжение=0.5
Натяжение=0.99

55. Радиальные базисные функции«Radial Basic Function»

Радиальные базисные функции«Radial Basic
N
f ( x, y, z ) i (ri )
Function»
i 1
где ri – декартово расстояние между i-й исходной точкой и текущим узлом сетки;
- РБФ, аргументом которой является расстояние ri; i – весовой коэффициент i - й
исходной точки, который характеризует степень влияния этой точки на текущий
узел сетки; N – количество исходных точек
1 (r11 ) 2 (r12 ) ... N (r1N ) Z1
1 (r21 ) 2 (r22 ) ... N (r2 N ) Z 2
.
.
1 (rN1 ) 2 (rN 2 ) ... N (rNN ) Z N
2
2
(
ri
)
h
R
мультиквадратичная функция
где h – это нормированное,
относительное расстояние(ri) от узла
сетки до исходной точки, «R2
РБФ-методы это точные
Parameter»– сглаживающий фактор, чем
интерполяторы. Параметр сглаживания
он больше тем меньше влияние
позволяет регулировать гладкость
расстояния от точки до узла сетки на
получаемой поверхности.

56. Модифицированный метод Шепарда

• Этот метод работает в тех же предположениях, что и метод
обратных
расстояний, но
позволяет
уменьшить
ошибки
свойственные методу обратных расстояний. В качестве оценки
переменной Z в произвольной точке (X0, Y0) области исследования
используется среднее взвешенное значений аппроксимирующих
функций в этой точке:
d max 0 di 0
wi 0
d
d
max 0 i 0
2

57. Полиномиальная регрессия

Метод используется для оценки пространственного тренда в данных, то есть
зависимости изучаемой пространственной переменной Z от координат X, Y. Этот
метод не является интерполяционным в прямом смысле: он не пытается
предсказать неизвестные значения Z. Он предназначен для выявления
глобальных пространственных трендов и теряет детальную локальную
информацию, содержащуюся в данных.
Уравнение полиномиальной регрессии Z на X, Y строится с использованием
метода наименьших квадратов на основе всех входных данных (окрестность
поиска не применяется), и метод можно считать глобальным и сглаживающим
интерполятором. Оценкой переменной Z в произвольной точке исследуемой
области будет значение, вычисленное по полученному уравнению регрессии:
• где Q(X,Y)- построенный полином

58. Локальные полиномы:

Этот метод также оценивает зависимость
пространственной переменной Z от
координат X, Y, но в отличие от
предыдущего
использует
кусочнополиномиальное интерполирование.
Он строит полиномиальную регрессию Z
на X, Y по данным, попавшим в
поисковый эллипс с центром в заданной
точке области исследования, получая,
таким
образом,
полиномиальное
приближение в локальной окрестности
этой точки.

59. Кусочно-полиномиальное интерполирование

• Z(x,y)=a+bx+cy – степень 1
• Z(x,y)=a+bx+cy+dxy+ex2+fx2 – степень 2
• Z(x,y)=a+bx+cy+ dxy+ex2+fx2+gx2y+hxy2+ix3+iy3 – степень 3
Количество точек участвующих в расчетах определяется поисковым эллипсом
При использовании большего количеств точек, чем нужно для точного
решения вместо абсолютного значения в точке используется взвешенное
значение, вес рассчитывается следующим образом Wi=(1-Ri)P где Ri –
нормализованное расстояние до i – го узла регулярной сетки изменяющееся
от 0 до 1(например, от точки Р1 до узла Т3 делится на расстояние от точки
Р_max до узла T3), Wi – весовой коэффициент расстояние до i – го узла
регулярной сетки; p – степень.

60. Изменение степени локального полинома

Степень 1
Степень 2
Степень 3

61. Изменение степени при расчете весов

Степень 1
Степень 2
Степень4

62. Дополнительная информация при построении ЦМВ по точкам:

При
оценке
значений
пространственной переменной могут
приниматься в расчет известные линии нарушения пространственной
непрерывности и/или
линии
разломов
в
области
исследования.
Примерами таких структурных нарушений являются тектонические
разломы,
геохимические
барьеры, линейные антропогенные
сооружения (дамбы, дороги) и реки.
X1, Y1, Z1
X2, Y2, Z2
…
Xm, Ym, Zm,
«Breakline» - линии
предоставляют
дополнительную
информацию,
которая может быть задействована
при моделировании.
Для
точки
интерполяции
находят ближайшую
точку, расположенную
на
линии
нарушений,
и
с
помощью
линейной интерполяции между двумя
вершинами вычисляют
в ней
значение Z Это
значение
затем
используется, наряду со значениями
в выборочных точках, для оценки Z в
точке интерполяции.

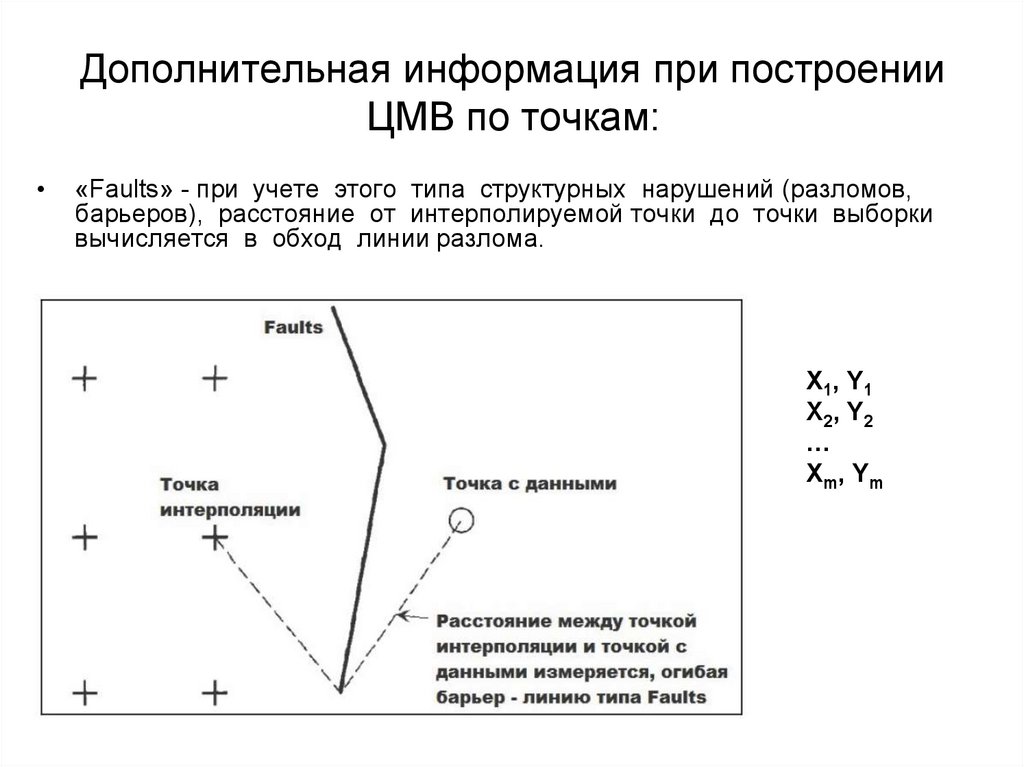
63. Дополнительная информация при построении ЦМВ по точкам:

«Faults» - при учете этого типа структурных нарушений (разломов,
барьеров), расстояние от интерполируемой точки до точки выборки
вычисляется в обход линии разлома.
X1, Y1
X2, Y2
…
Xm, Ym

64.

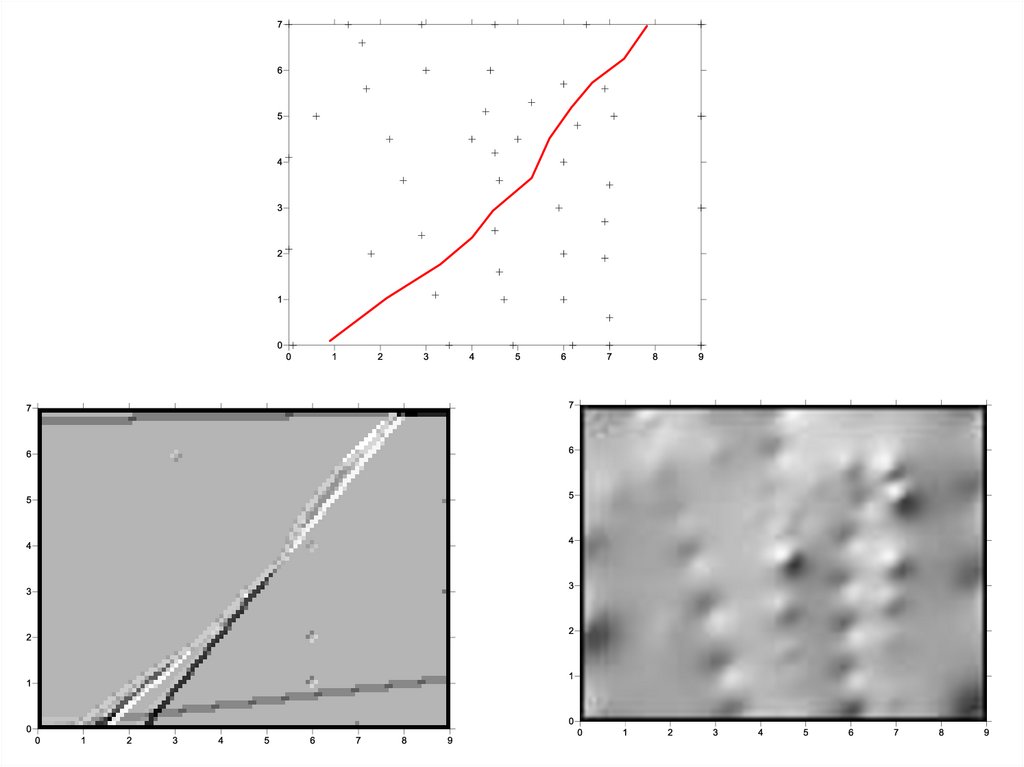
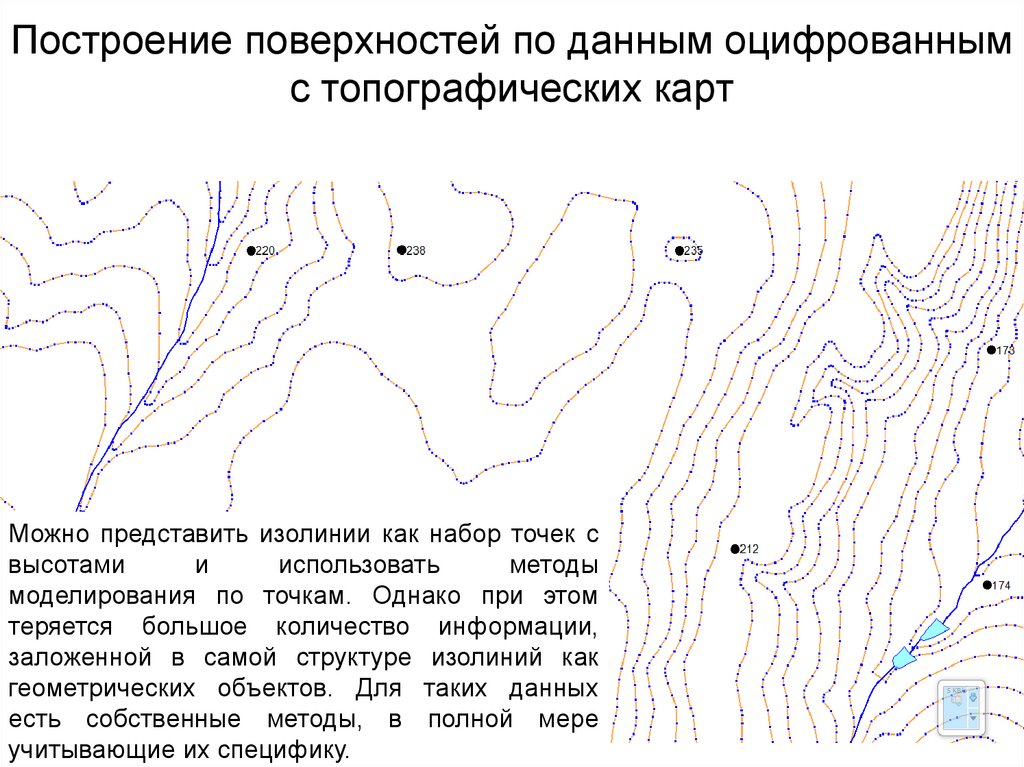
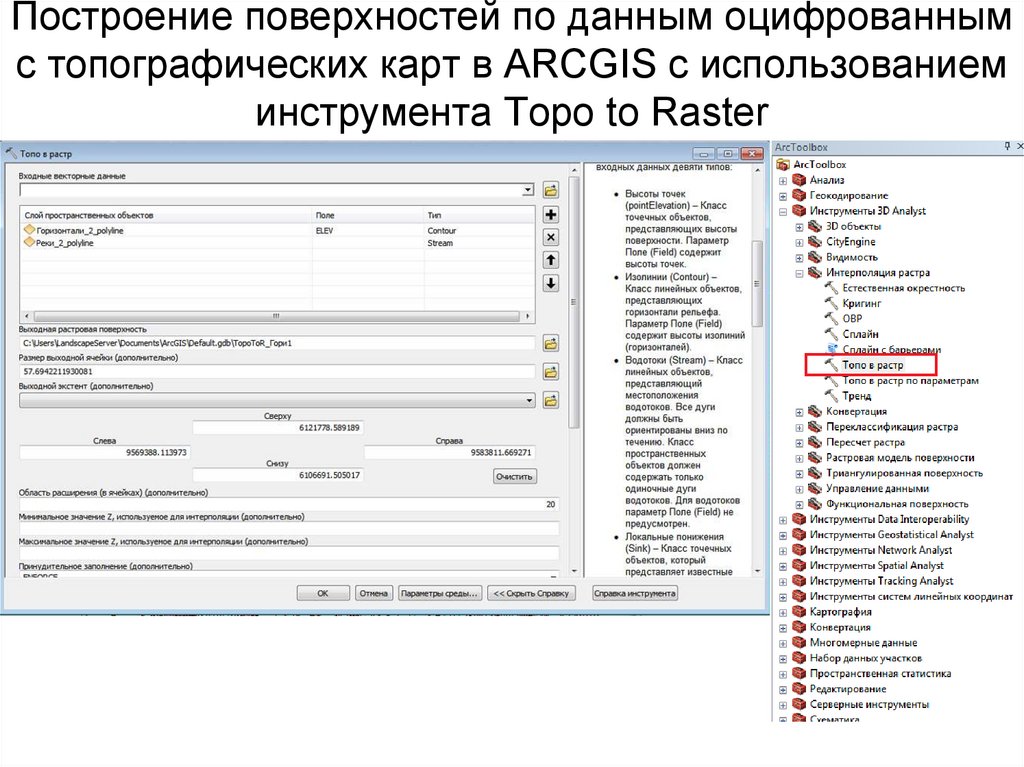
65. Построение поверхностей по данным оцифрованным с топографических карт

Можно представить изолинии как набор точек с
высотами
и
использовать
методы
моделирования по точкам. Однако при этом
теряется большое количество информации,
заложенной в самой структуре изолиний как
геометрических объектов. Для таких данных
есть собственные методы, в полной мере
учитывающие их специфику.

66. Построение поверхностей по данным оцифрованным с топографических карт в ARCGIS c использованием инструмента Topo to Raster

Виды тематической информации:
Изолинии (горизонтали) «Contours» - Класс линейных объектов, представляющих горизонтали
рельефа. Параметр Поле (Field) содержит высоты изолиний (горизонталей);
Реки, потоки «Streams» - Класс линейных объектов, представляющий местоположения
водотоков. Все дуги должны быть ориентированы вниз по течению. Класс пространственных
объектов должен содержать только одиночные дуги водотоков. Для водотоков параметр Поле
(Field) не предусмотрен;
Озера «Lakes» - Класс полигональных объектов, который задает местоположение озер. Всем
ячейкам выходного растра, попадающим внутрь озера, будет присвоено минимальное значение
высоты из всех высот всех ячеек, расположенных вдоль береговой линии. Для озер параметр
Поле (Field) не применяется;
Локальные западины «Sinks» - Класс точечных объектов, который представляет известные
локальные топографические понижения. Инструмент Топо в Растр (Topo to Raster) не будет
пытаться убрать из анализа точки, которые явно определены как локальные понижения. Параметр
Поле (Field) должен указывать поле, в котором хранятся высоты допустимых локальных
понижений.
Точки отметок высот «Point elevation» - Класс точечных объектов, представляющих высоты
поверхности. Параметр Поле (Field) содержит высоты точек;
Обрывы «Cliffs» - Класс линейных объектов, представляющий обрывы. Линейные объектыобрывы должны иметь направление, при этом левая стороны линии должны соответствовать
низкой стороне обрыва, а правая – высокой. Для скал опция Поле (Field) не предусмотрена.

67. Построение поверхностей по данным оцифрованным с топографических карт.

Как и в случае моделирования по данным в точках, задача моделирования по
изолиниям сводится к восстановлению значения высоты в произвольной точке
области моделирования, основанного на исходных данных.
Выделяют 5 групп методов:
вычисление среднего значения по четырем профилям(метод Дугласа);
интерполяция на основе триангуляции с ограничениями;
интерполяция с использованием топологического расстояния;
численное решение дифференциального уравнения, описывающего
сплайны с натяжением, с заданными граничными условиями в
некоторых точках на изолиниях.

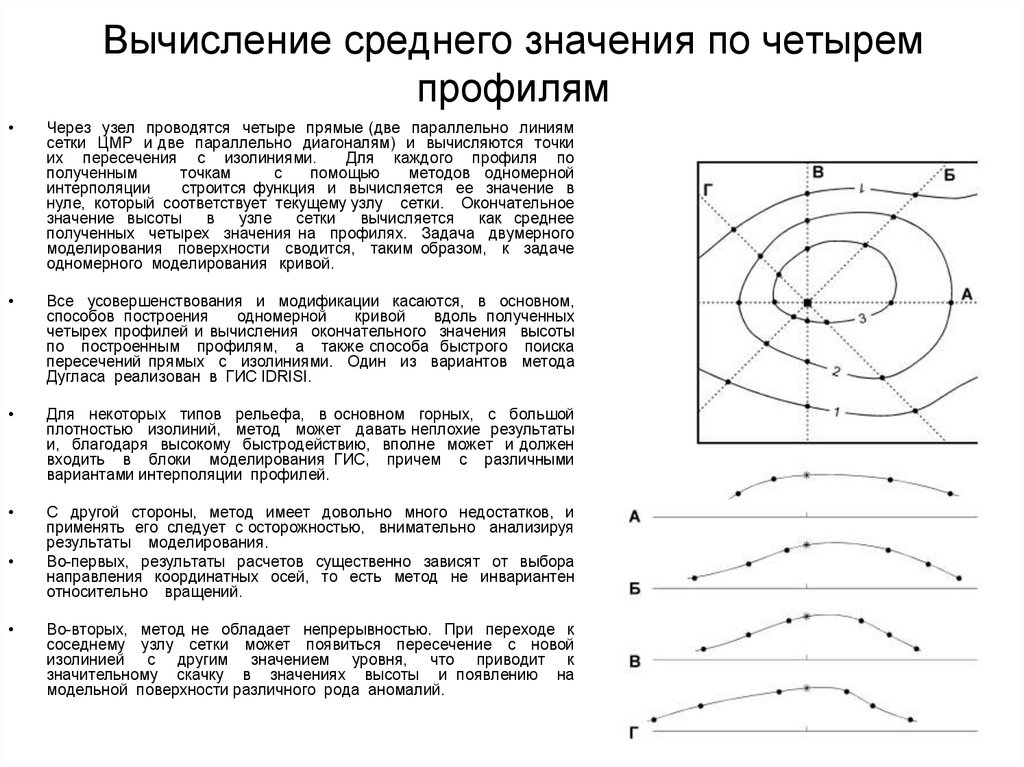
68. Вычисление среднего значения по четырем профилям

Через узел проводятся четыре прямые (две параллельно линиям
сетки ЦМР и две параллельно диагоналям) и вычисляются точки
их пересечения с изолиниями.
Для каждого профиля по
полученным
точкам
с
помощью
методов одномерной
интерполяции
строится функция и вычисляется ее значение в
нуле, который соответствует текущему узлу сетки. Окончательное
значение высоты
в
узле
сетки
вычисляется
как среднее
полученных четырех значения на профилях. Задача двумерного
моделирования поверхности сводится, таким образом, к задаче
одномерного моделирования кривой.
Все усовершенствования и модификации касаются, в основном,
способов построения
одномерной
кривой
вдоль полученных
четырех профилей и вычисления окончательного значения высоты
по построенным профилям, а также способа быстрого поиска
пересечений прямых с изолиниями. Один из вариантов метода
Дугласа реализован в ГИС IDRISI.
Для некоторых типов рельефа, в основном горных, с большой
плотностью изолиний, метод может давать неплохие результаты
и, благодаря высокому быстродействию, вполне может и должен
входить в блоки моделирования ГИС, причем с различными
вариантами интерполяции профилей.
С другой стороны, метод имеет довольно много недостатков, и
применять его следует с осторожностью, внимательно анализируя
результаты моделирования.
Во-первых, результаты расчетов существенно зависят от выбора
направления координатных осей, то есть метод не инвариантен
относительно вращений.
Во-вторых, метод не обладает непрерывностью. При переходе к
соседнему узлу сетки может появиться пересечение с новой
изолинией с другим значением уровня, что приводит к
значительному скачку в значениях высоты и появлению на
модельной поверхности различного рода аномалий.

69. Интерполяция на основе триангуляции с ограничениями:

Методы второй группы основаны на построении по
исходным
данным структуры так называемой
триангуляции Делоне с ограничениями, в которой
некоторые
ребра
триангуляции
заранее
фиксируются (в данном случае это ребра,
образуемые соседними точками на изолиниях), и
последующего восстановления
поверхности
путем линейной интерполяции на треугольниках.
В
простейшем
базовом
варианте метод
реализован в модуле 3D-Analyst ГИС ArcView.
По своей конструкции такой подход позволяет учитывать топологическую
структуру изолиний, а также дополнительные исходные данные для
моделирования в виде структурных линий, объектов гидрографии, высотных
отметок. Основной недостаток
метода в его базовом варианте состоит в том,
что
в
построенной
триангуляции могут встретиться треугольники, все вершины которых лежат
на изолиниях одного уровня, что приводит к появлению на модели
горизонтальных участков Горизонтальные треугольники могут
устраняться как путем добавления вручную к исходным изолиниям отдельных
точек с высотами и структурных линий с интерполированной заранее вдоль
них высотой, так и автоматическим созданием
таких
объектов
по
геометрической форме и топологической структуре изолиний.

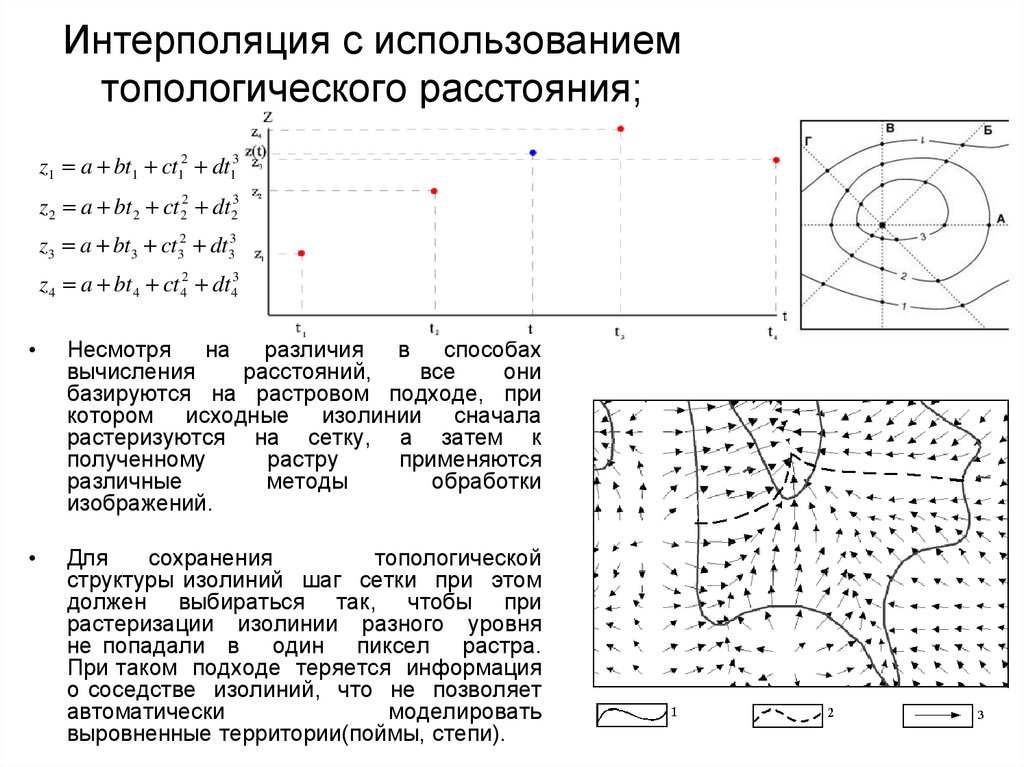
70. Интерполяция с использованием топологического расстояния;

z1 a bt1 ct12 dt13
z2 a bt 2 ct 22 dt 23
z3 a bt3 ct32 dt33
z4 a bt 4 ct 42 dt 43
Несмотря на различия
в способах
вычисления
расстояний,
все
они
базируются на растровом подходе, при
котором исходные изолинии сначала
растеризуются на сетку, а затем к
полученному
растру
применяются
различные
методы
обработки
изображений.
Для
сохранения
топологической
структуры изолиний шаг сетки при этом
должен выбираться так, чтобы при
растеризации изолинии разного уровня
не попадали в один пиксел растра.
При таком подходе теряется информация
о соседстве изолиний, что не позволяет
автоматически
моделировать
выровненные территории(поймы, степи).

71. Численное решение дифференциального уравнения, описывающего сплайны с натяжением, с заданными граничными условиями в некоторых

точках на
изолиниях:
Здесь используются сплайны с натяжением, но не в явном виде
радиальной интерполяции, а как численное решение дифференциального
уравнения в частных производных четвертого порядка. Для сплайнов
минимальной кривизны это бигармоническое уравнение:
где ∇2 - оператор Лапласа,
δ (x,y)
дельта-функция Дирака, (xi, yi)- опорные
точки, получаемые путем дискретизации изолиний, zi
- значения функции в опорных
точках. В отличие от традиционной сплайн интерполяции такой подход мало чувствителен к
нерегулярности расположения
точек,
что
позволяет использовать его для
изолинейных исходных данных.
Применительно к изолиниям этот подход активно разрабатывался Хатчинсоном. На
основе предложенного им метода разработана программа ANUDEM. Позднее
этот
алгоритм был использован в модуле TOPOGRID(Topo to Raster) ArcGIS. Основываясь на
численных экспериментах, Хатчинсон предложил оптимальное значение параметра
натяжения, а также способ включения в процесс моделирования объектов гидрографии
и способ устранения локальных впадин на уже построенной модели с целью создания
гидрологически
корректных
ЦМР. Разработанный им метод является наиболее
популярным в настоящее время.

72. Построение поверхностей по данным оцифрованным с топографических карт в ARCGIS c использованием инструмента Topo to Raster

73.

74. Факторы влияющие на результаты морфометрического анализа

• Изрезанность (изменчивость) анализируемой
земной поверхности;
• Точности измерений (какой метод
использовался для сбора данных );
• Разрешение модели (шаг сетки);
• Метод восстановления поверхности
(математический алгоритм расчета значений
в узлах сетки);
• Тип геоморфометрического анализа (для
какого геоморфометрического анализа мы
собираемся использовать данную ЦМВ)

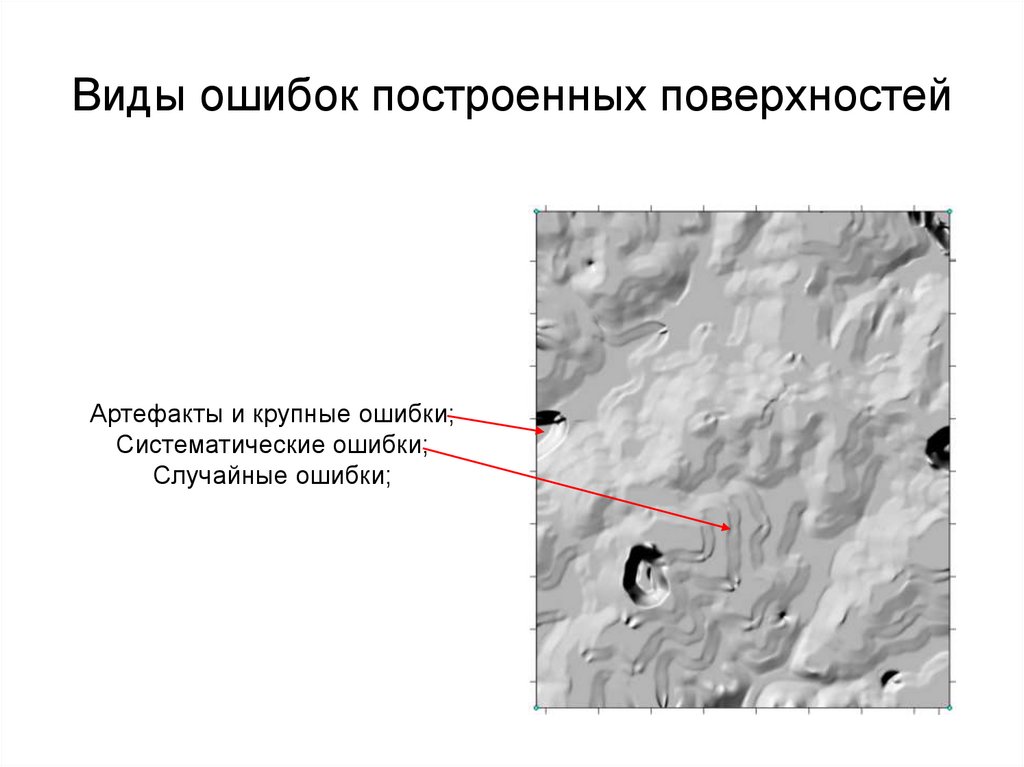
75. Виды ошибок построенных поверхностей

Артефакты и крупные ошибки;
Систематические ошибки;
Случайные ошибки;

76. Подходы при количественном описании ошибок

• Оценка ошибок на основе
исходного набора данных.
ЦМВ
и
• Оценка ошибок на основе
независимого набора данных.
ЦМВ
и
• Перекрестная проверка.

77. Показатели для количественного описания ошибок ЦМВ

n
• Среднеквадратичная
ошибка/root mean square
error
СКО
[ z( s ) z ( s )]
i 1
i
ref
2
i
n
n
• Средняя ошибка/ mean
error
[ z( s z ( s )]
ME i 1
i
ref
i
n
• Стандартное
отклонение
ошибки/
standard deviation of error
• где z(si) и zref(si) высота в определенной точке на ЦМВ и в
проверочном наборе данных соответственно

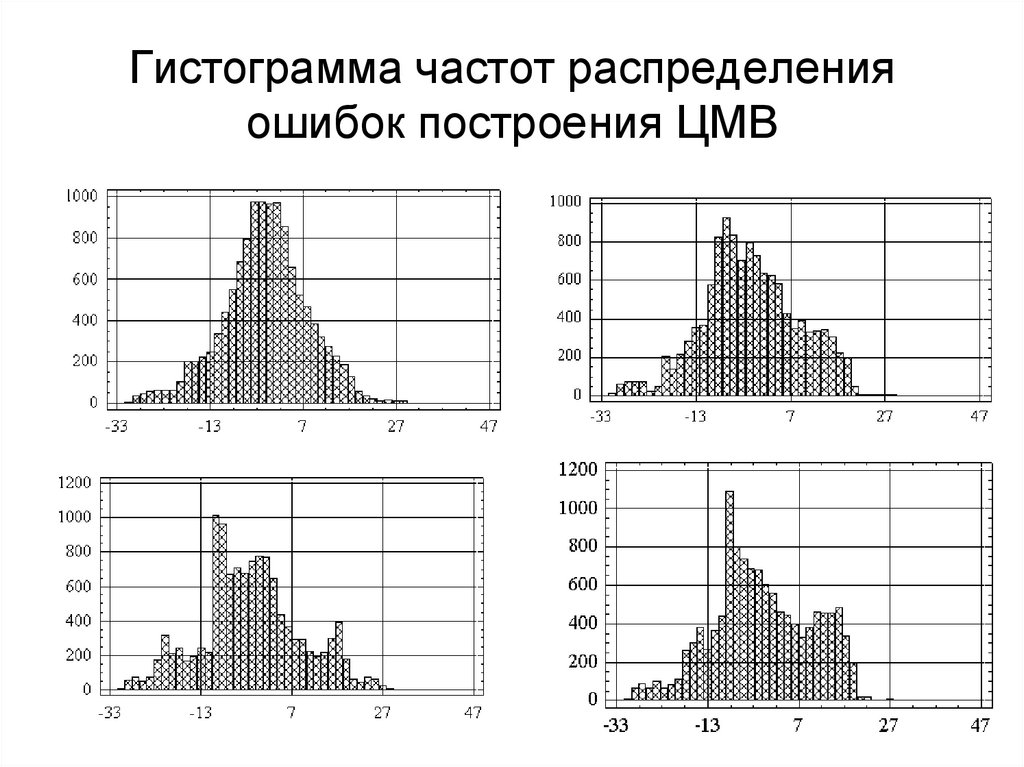
78. Гистограмма частот распределения ошибок построения ЦМВ

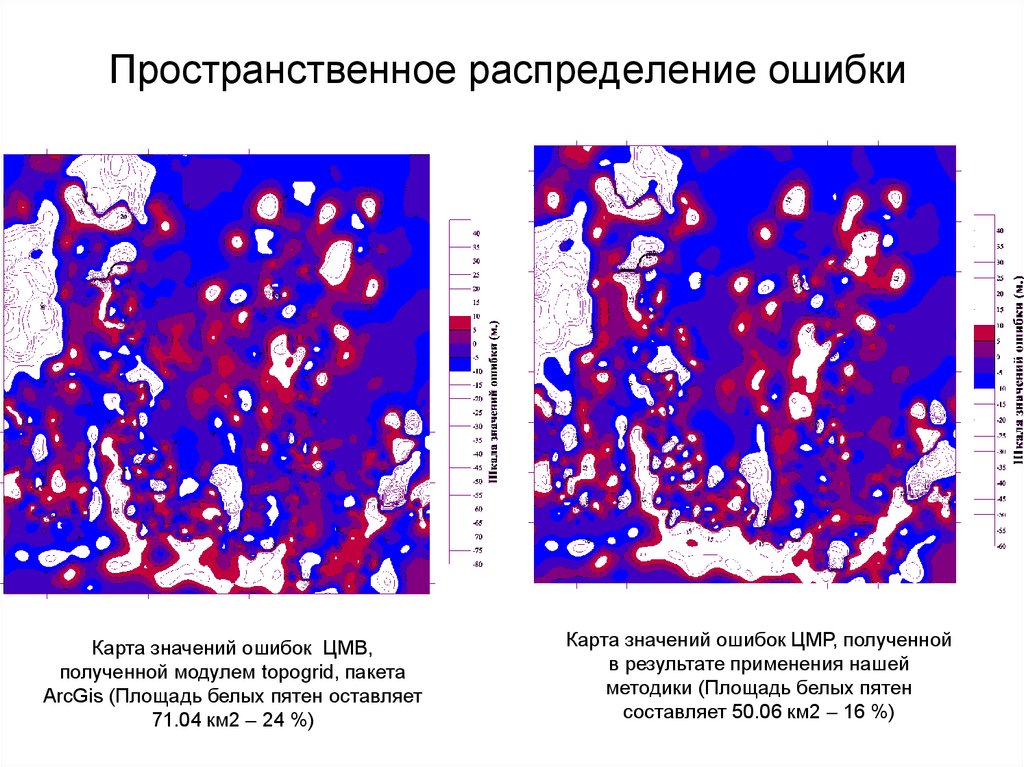
79. Пространственное распределение ошибки

Карта значений ошибок ЦМВ,
полученной модулем topogrid, пакета
ArcGis (Площадь белых пятен оставляет
71.04 км2 – 24 %)
Карта значений ошибок ЦМР, полученной
в результате применения нашей
методики (Площадь белых пятен
составляет 50.06 км2 – 16 %)

80. Сглаживающие фильтры для сокращения ошибок

• Фильтром
в
данном
случае
называют
математический алгоритм, который оценивает
значение в узле регулярной сетки на основе
значений в окружающих его узлах. Два фактора
определяющие результат работы фильтра:
• 1)Размер фильтра
• 2) Значения весов в ячейках фильтра

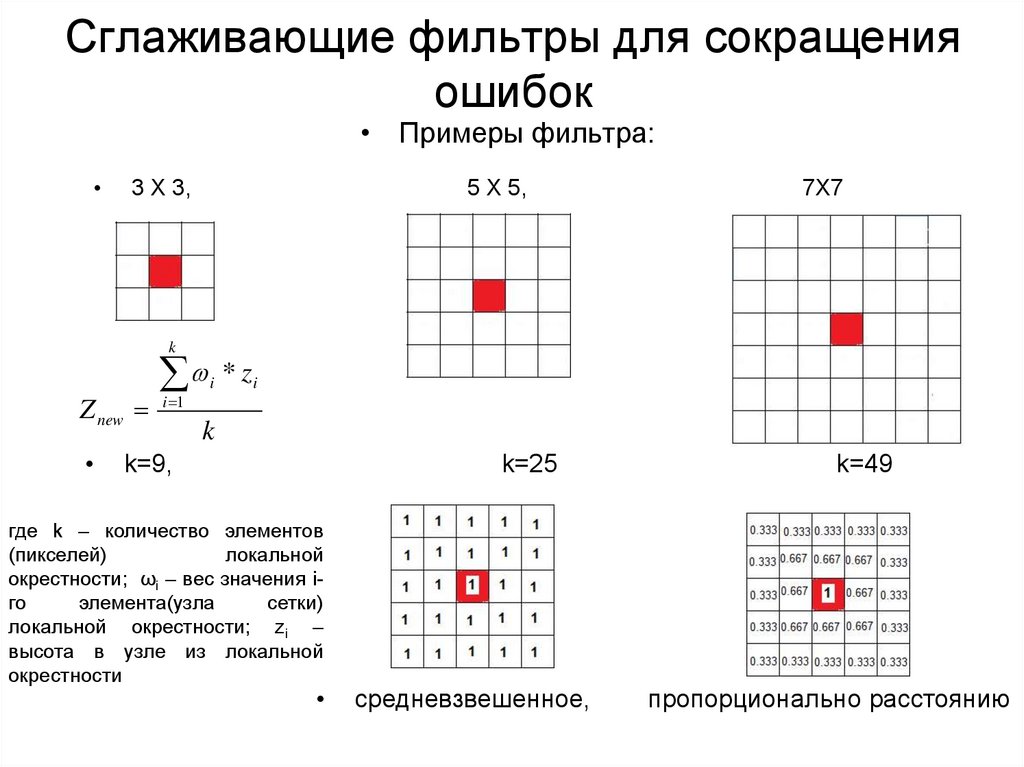
81. Сглаживающие фильтры для сокращения ошибок

• Примеры фильтра:
3 Х 3,
5 Х 5,
7Х7
k
Z new
* z
i 1
i
i
k
k=9,
k=25
где k – количество элементов
(пикселей)
локальной
окрестности; ωi – вес значения iго
элемента(узла
сетки)
локальной окрестности; zi –
высота в узле из локальной
окрестности
средневзвешенное,
k=49
пропорционально расстоянию

82. Результат сглаживания фильтрами разных размеров

9Х9
5Х5
7Х7

83.

• Surfer
• TAS
• GRASS
• ARCGIS
• LandSurf
• ЭКО
• Evans
• Krcho
• Wood
• Pike
• Шарый
• Ласточкин
http://gis-lab.info/qa/geomorphometric-parameters-theory.html#math_3

84.

Геморфометрический анализ растровых ЦМР базируется на двух исходных
положениях. Первое основывается на математической формализации
земной поверхности.
1) z = Ax2 + By2 + Cxy + Dx + Ey + F (Evans 1980)
2) z = Ax2y2 + Bx2y + Cxy2 + Dx2 + Ey2 + Fxy + Gx + Hy + I (Zevenbergen,
Thorne 1987)
rx 2
ty2
3) z 2 sxy 2 px qy (Young, 1978);
Второе предусматривает расчет показателя в точке (пикселе) с учетом
окружения.

85.

Наиболее
фундаментальными
и
наиболее
употребимыми
геморфометрическими параметрами являются уклон и экспозиции.
Параметры уклона и экспозиции взаимосвязаны, т.к. оба эти показателя
характеризуют градиент поверхности, т.е. интенсивность изменения ее
значений в пространстве, которая может быть выражена производной
первого порядка.
Как производная поверхности первого порядка, градиент характеризуется
величиной (уклоном) и направлением (экспозицией).
z = Ax2 + By2 + Cxy + Dx + Ey + F
Если поместить начало системы координат в
центральную ячейку, то координаты X и Y в этой
ячейке =0

86.

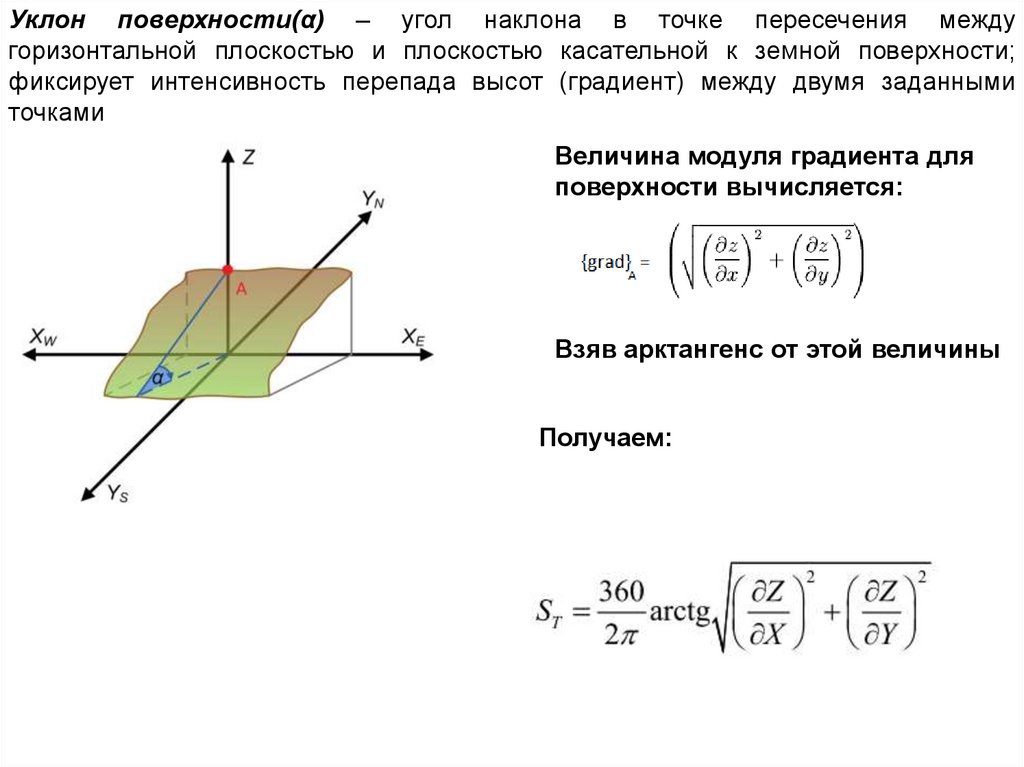
Уклон поверхности(α) – угол наклона в точке пересечения между
горизонтальной плоскостью и плоскостью касательной к земной поверхности;
фиксирует интенсивность перепада высот (градиент) между двумя заданными
точками
Величина модуля градиента для
поверхности вычисляется:
Взяв арктангенс от этой величины
Получаем:

87.

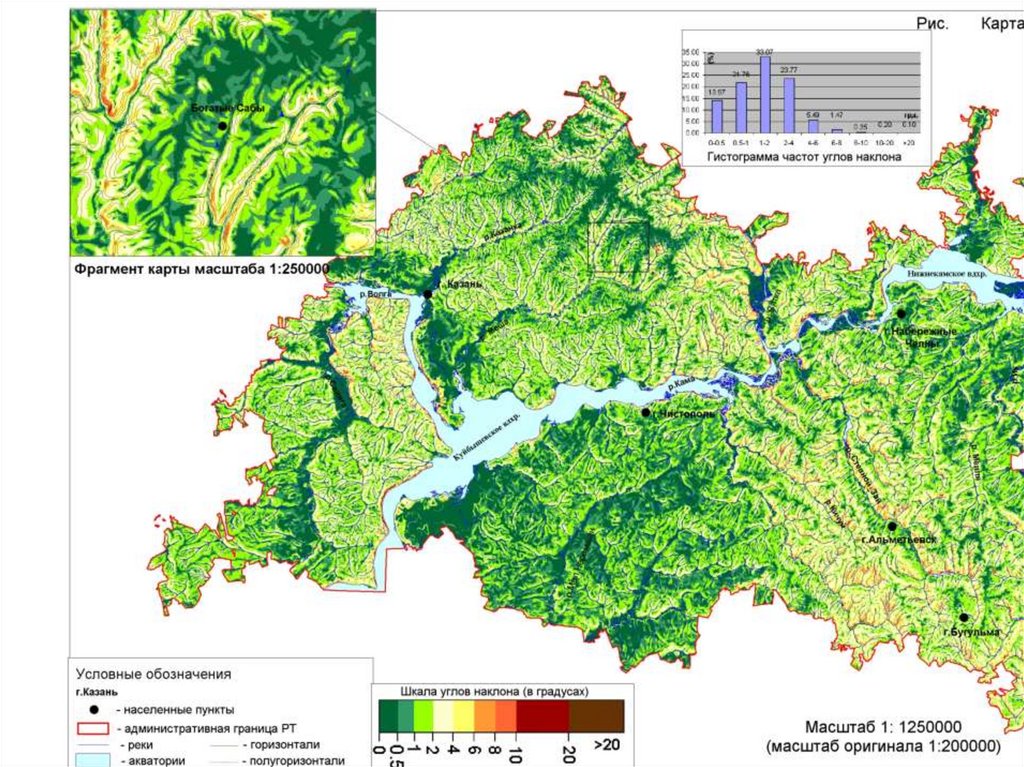
Уклон поверхности закономерно связан со следующими процессами и характеристиками
ландшафта:
поверхностный сток и дренирование – чем более крутой склон, тем интенсивнее поверхностный сток и
меньше инфильтрация влаги в почвенную толщу. Таким образом, уклон имеет принципиальное значение
для режима увлажнения почв, особенно – верхних слоев;
эрозия – интенсивность эрозии растет экспоненциально с увеличением уклона. Это объясняется тем, что
с увеличением градиента кинетическая энергия осадков остается постоянной, но транспорт ускоряется в
направлении подножья склона. В результате, кинетическая энергия стока превышает кинетическую
энергию осадков, когда склон переходит отметку 8,5°, что и способствует проявлению эрозионных
процессов;
мощность почвенного профиля на склоне закономерно изменяется в соответствии с уклоном и
относительной высотой. Как правило, почвенная толща меньше на возвышенных наклонных участках
вследствие эрозионных процессов и гравитационного перемещения материала, и постепенно
увеличивается в направлении пониженных участков с небольшим уклоном;
количество солнечной энергии также зависит от уклона, поскольку он определяет угол падения
солнечных лучей на земную поверхность. Увеличение уклона поверхности в направлении поступления
солнечных лучей увеличивает угол их падения, а значит – количество энергии, которое получает
поверхность. Это определяет микроклиматические особенности участка, в частности температуру,
эвапотранспирацию и влажность верхних слоев почвы;
Как правило, значения показателя измеряются в градусах (также это могут быть проценты или
радианы) и колеблются в диапазоне от 0° (горизонтальная плоскость) до 90° (вертикальная
плоскость).

88.

d
z3 z6 z9 z1 z 4 z7
6w
z z z z z z
e 1 2 3 7 8 9
6w
d
Z6 Z4
2w
e
Z 2 Z8
2w

89.

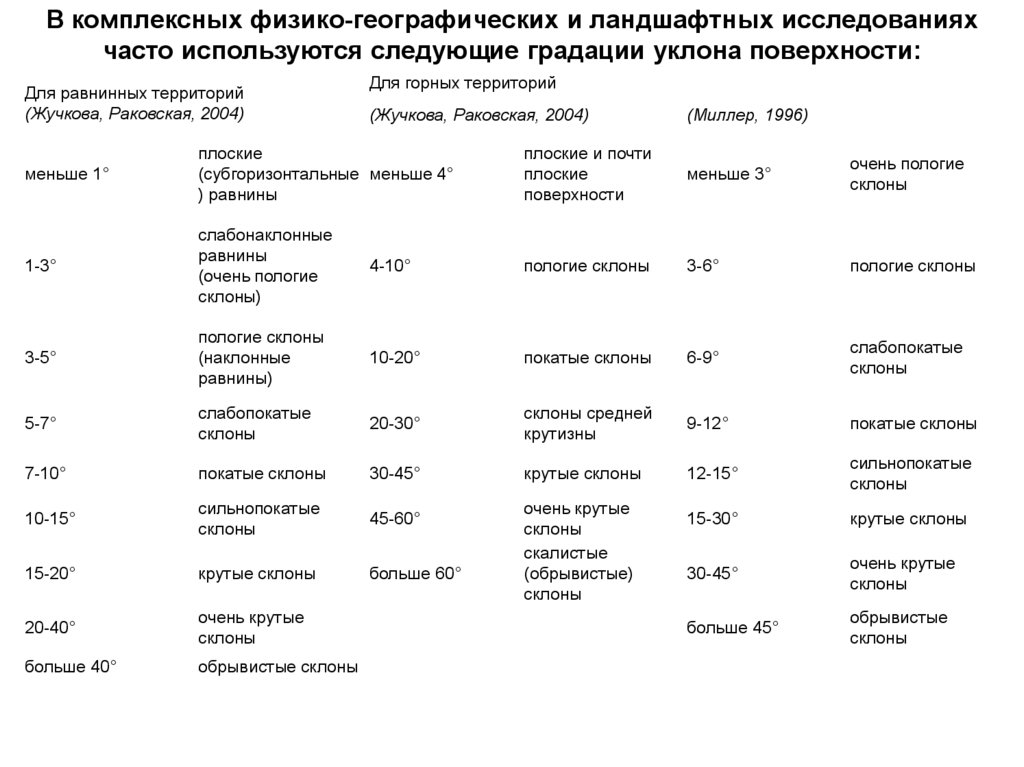
В комплексных физико-географических и ландшафтных исследованиях
часто используются следующие градации уклона поверхности:
Для равнинных территорий
(Жучкова, Раковская, 2004)
Для горных территорий
(Жучкова, Раковская, 2004)
(Миллер, 1996)
меньше 1°
плоские
(субгоризонтальные меньше 4°
) равнины
плоские и почти
плоские
поверхности
меньше 3°
очень пологие
склоны
1-3°
слабонаклонные
равнины
(очень пологие
склоны)
4-10°
пологие склоны
3-6°
пологие склоны
3-5°
пологие склоны
(наклонные
равнины)
10-20°
покатые склоны
6-9°
слабопокатые
склоны
5-7°
слабопокатые
склоны
20-30°
склоны средней
крутизны
9-12°
покатые склоны
7-10°
покатые склоны
30-45°
крутые склоны
12-15°
сильнопокатые
склоны
10-15°
сильнопокатые
склоны
45-60°
15-30°
крутые склоны
15-20°
крутые склоны
больше 60°
30-45°
очень крутые
склоны
20-40°
очень крутые
склоны
больше 45°
обрывистые
склоны
больше 40°
обрывистые склоны
очень крутые
склоны
скалистые
(обрывистые)
склоны

90.

91.

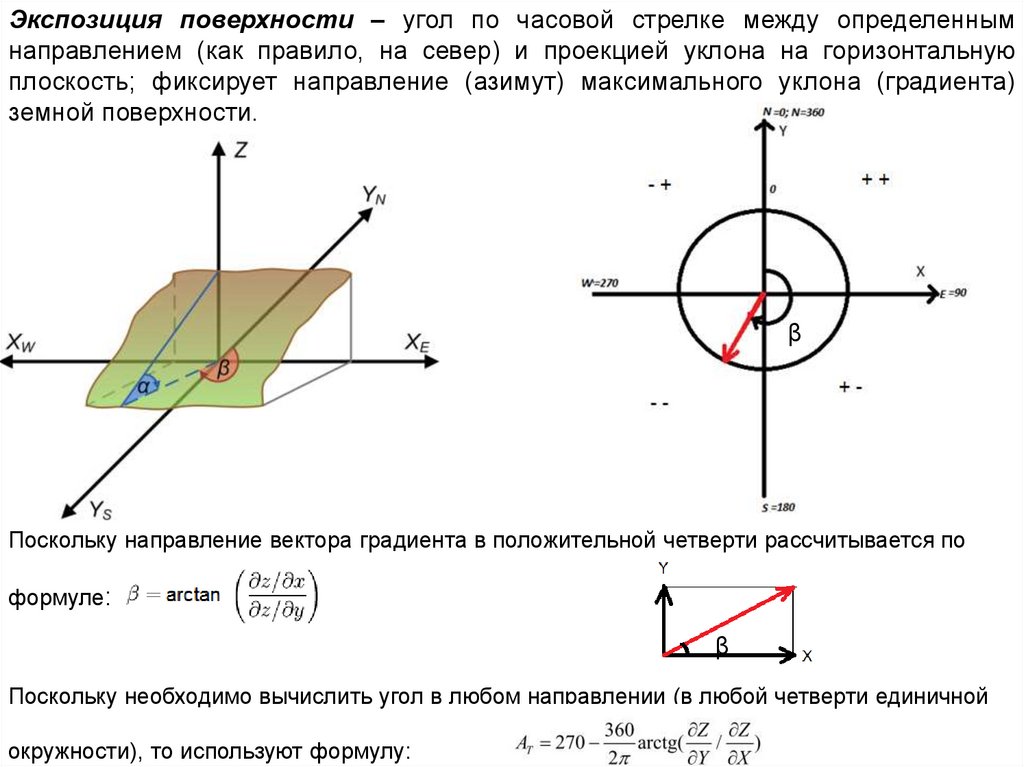
Экспозиция поверхности – угол по часовой стрелке между определенным
направлением (как правило, на север) и проекцией уклона на горизонтальную
плоскость; фиксирует направление (азимут) максимального уклона (градиента)
земной поверхности.
β
Поскольку направление вектора градиента в положительной четверти рассчитывается по
формуле:
β
Поскольку необходимо вычислить угол в любом направлении (в любой четверти единичной
окружности), то используют формулу:

92.

Функциональная интерпретация экспозиции может вестись в нескольких
направлениях, поскольку она характеризует:
основное направление линий тока, т.е. когда вода (или другой способный к
перемещению материал) движется под действием силы тяжести вниз по склону,
он делает это в направлении, которое определяется экспозицией.
Эта зависимость положена в основу гидрологических алгоритмов
моделирования поверхностного стока.
ориентацию участка по отношению к потоку солнечных лучей, а значит и
количество радиации, получаемой земной поверхностью – инсоляцию.
Благодаря этому экспозиция существенно влияет на локальный климат
(микроклимат) участка. Например, в северном полушарии склоны южной
экспозиции прогреваются лучше, чем северной. Кроме того, вследствие большей
эвапотранспирации (испарения) южные склоны суше северных. Количество
солнечной радиации непосредственно определяет интенсивность развития
растений и их биологическую продуктивность. Такие закономерности иногда
обуславливают довольно-таки существенные азональные и локальные отличия в
почвенном и растительном покрове, сезонном течении функциональных
процессов в живых организмах и ландшафтах в целом.

93.

Отмеченные выше особенности распределения тепла дополнительно усложняются тем, что
склоны восточной и западной ориентации демонстрируют контрастность тепловых условий.
Это объясняется тем, что на восточные склоны солнечные лучи попадают в утренние
прохладные часы и тратятся на прогревание поверхности, а западные склоны освещаются во
второй половине дня, когда поверхность уже прогрета. В результате, западные склоны
несколько теплее и суше, чем восточные. М. Гродзинский (2013) отмечает, что при весьма
значительной крутизне склонов (особенно в горных ландшафтах) склоны юго-западной
экспозиции оказываются тепле и суше, чем южной экспозиции, а склоны северо-восточной
экспозиции – холоднее и влажнее, чем северные. Еще раньше эту особенность отметил Р.
Уиттекер (1980), который самым холодным считает не северное, а северо-восточное
местоположение, а наиболее теплым – юго-восточное.
Типология инсоляционных местоположений проводится по сторонам горизонта (румбам)
северное
N
0-22.5°; 337.5360°
северовосточное
NE
22.5-67.5°
восточное
E
67.5-112.5°
юго-восточное
SE
112.5-157.5°
южное
S
157.5-202.5°
юго-западное
SW
202.5-247.5°
западное
W
247.5-292.5°
северо-западное
NW
292.5-337.5°

94.

95.

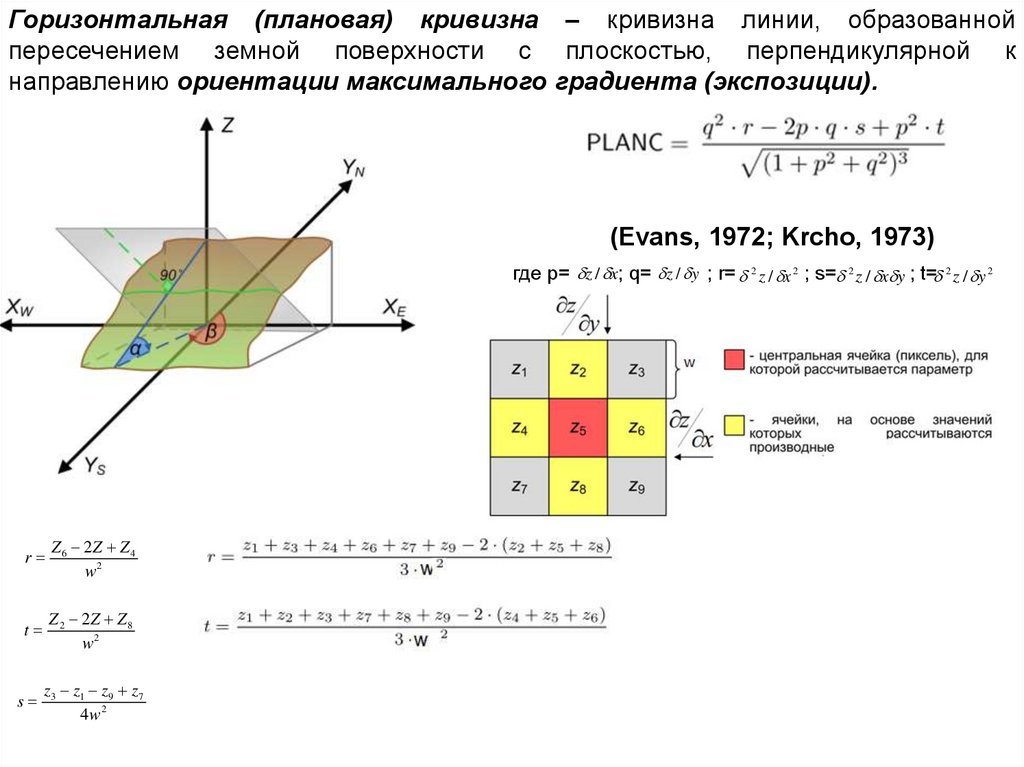
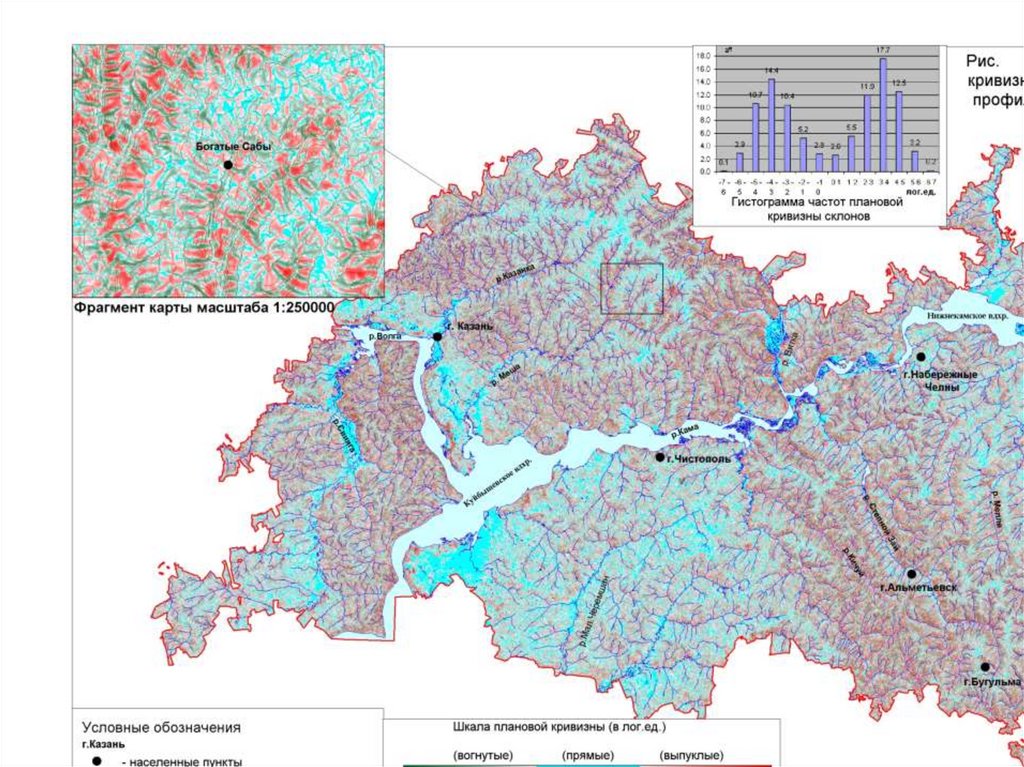
Горизонтальная (плановая) кривизна – кривизна линии, образованной
пересечением земной поверхности с плоскостью, перпендикулярной к
направлению ориентации максимального градиента (экспозиции).
(Evans, 1972; Krcho, 1973)
где p= z / x; q= z / y ; r= 2 z / x 2 ; s= 2 z / x y ; t= 2 z / y 2
r
Z 6 2Z Z 4
w2
t
Z 2 2Z Z8
w2
s
z3 z1 z9 z7
4w 2

96.

Единицами измерения кривизны земной поверхности являются 1/м, но в
результате расчетов получаются в основном очень маленькие значения,
потому для облегчения интерпретации рекомендуется умножать их на 100
или использовать 1 и 99% квантили(вместо min и max) для построения карт.
При интерпретации значений кривизны нужно обращать внимание как на
величину самого значения (модуль), так и на его знак.
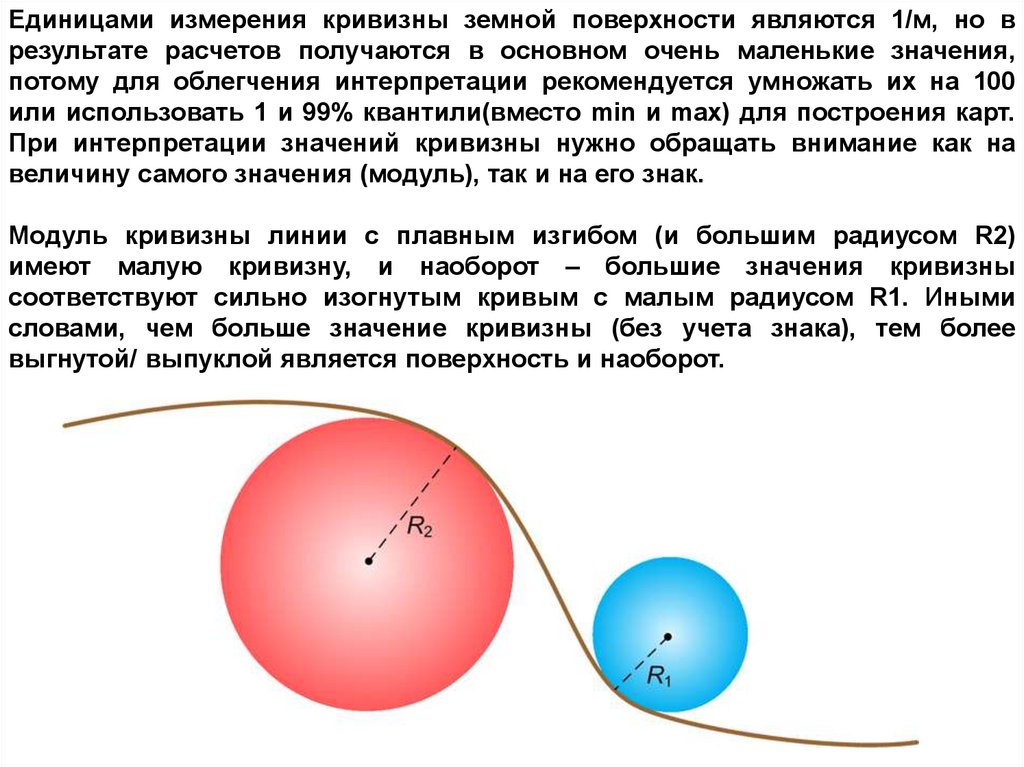
Модуль кривизны линии с плавным изгибом (и большим радиусом R2)
имеют малую кривизну, и наоборот – большие значения кривизны
соответствуют сильно изогнутым кривым с малым радиусом R1. Иными
словами, чем больше значение кривизны (без учета знака), тем более
выгнутой/ выпуклой является поверхность и наоборот.

97.

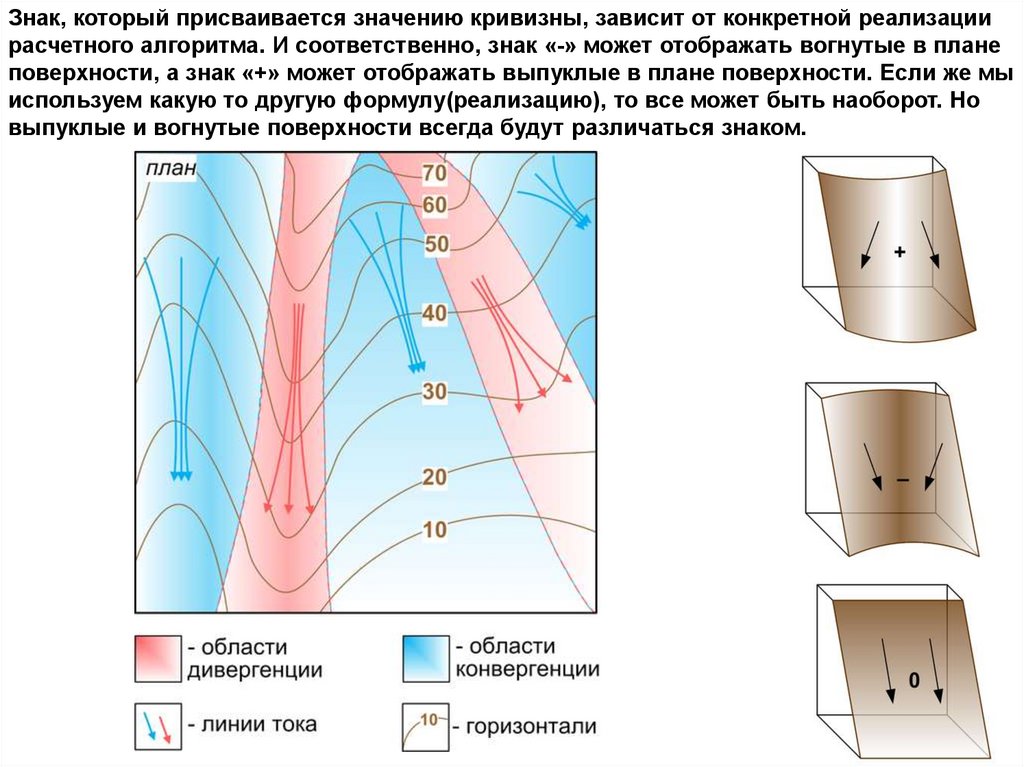
Знак, который присваивается значению кривизны, зависит от конкретной реализации
расчетного алгоритма. И соответственно, знак «-» может отображать вогнутые в плане
поверхности, а знак «+» может отображать выпуклые в плане поверхности. Если же мы
используем какую то другую формулу(реализацию), то все может быть наоборот. Но
выпуклые и вогнутые поверхности всегда будут различаться знаком.

98.

99.

Вертикальная (профильная) кривизна – кривизна линии, образованной пересечением
земной поверхности и вертикальной плоскости. Как производная второго порядка
вертикальная кривизна описывает градиент уклона вдоль заданного контура.
где p= z / x; q= z / y ; r= 2 z / x 2 ; s= 2 z / x y ; t= 2 z / y 2
Профильная кривизна – вертикальная составляющая второй производной
высоты, которая описывает меру изменения модуля градиента. При
интерпретации ее значений справедливы те же закономерности, что были
перечислены выше для горизонтальной кривизны. Единицами измерения так
же являются 1/м , которые для удобства умножаются на 100 или
используются квантили, т.е. вертикальная кривизна характеризует
изменение уклона поверхности на 100 м вдоль его основного направления.
Чем больше значения вертикальной кривизны, тем более выпуклая/ вогнутая
поверхность в заданном направлении.

100.

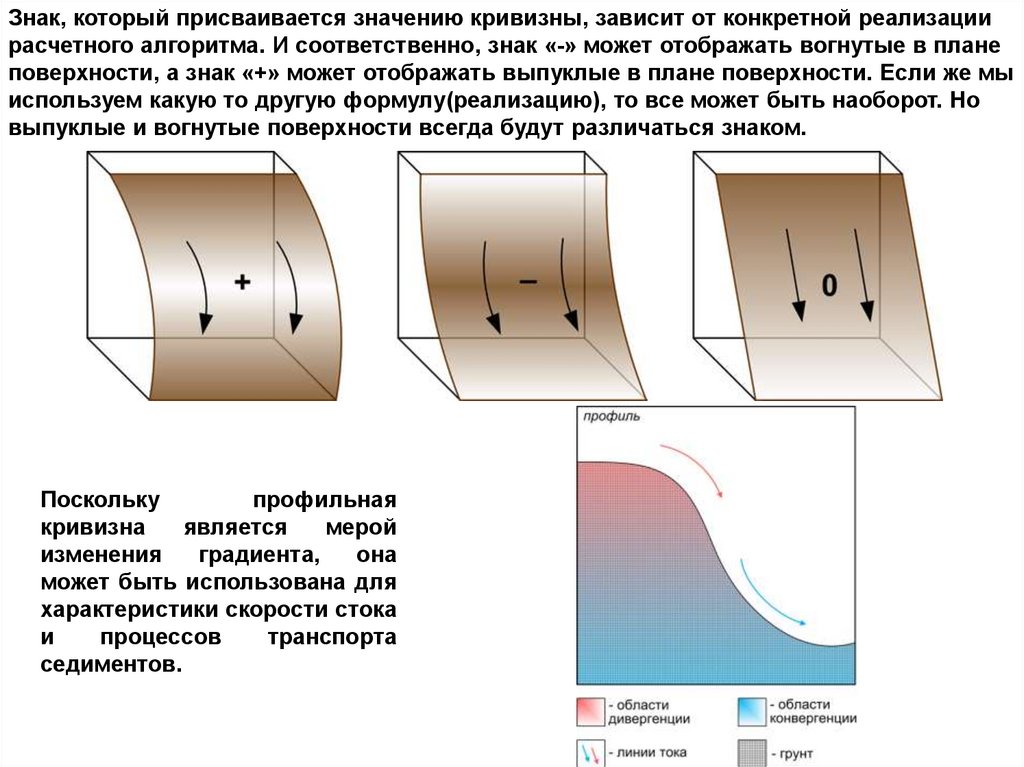
Знак, который присваивается значению кривизны, зависит от конкретной реализации
расчетного алгоритма. И соответственно, знак «-» может отображать вогнутые в плане
поверхности, а знак «+» может отображать выпуклые в плане поверхности. Если же мы
используем какую то другую формулу(реализацию), то все может быть наоборот. Но
выпуклые и вогнутые поверхности всегда будут различаться знаком.
Поскольку
профильная
кривизна
является
мерой
изменения
градиента,
она
может быть использована для
характеристики скорости стока
и
процессов
транспорта
седиментов.

101.

102.

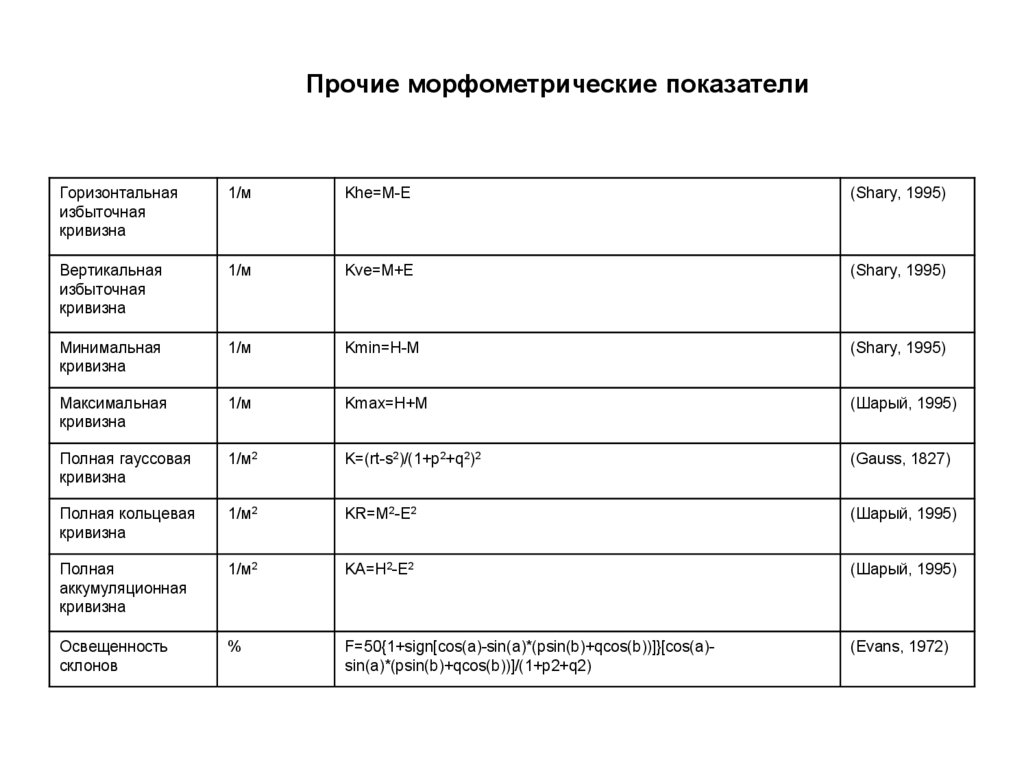
Прочие морфометрические показатели
Горизонтальная
избыточная
кривизна
1/м
Khe=M-E
(Shary, 1995)
Вертикальная
избыточная
кривизна
1/м
Kve=M+E
(Shary, 1995)
Минимальная
кривизна
1/м
Kmin=H-M
(Shary, 1995)
Максимальная
кривизна
1/м
Kmax=H+M
(Шарый, 1995)
Полная гауссовая
кривизна
1/м2
K=(rt-s2)/(1+p2+q2)2
(Gauss, 1827)
Полная кольцевая
кривизна
1/м2
KR=M2-E2
(Шарый, 1995)
Полная
аккумуляционная
кривизна
1/м2
KA=H2-E2
(Шарый, 1995)
Освещенность
склонов
%
F=50{1+sign[cos(a)-sin(a)*(psin(b)+qcos(b))]}[cos(a)sin(a)*(psin(b)+qcos(b))]/(1+p2+q2)
(Evans, 1972)

103. Моделирование гидрологических процессов с использованием ЦМР

Направление потока – направление перемещения масс (воды, почвогрунтов, загрязнителей и т.д.) по поверхности земли под действием силы
тяжести.
Направление потока – связано с экспозицией.
Конвергенция - концентрация потока масс в
ходе их перемещения по поверхности
земли. В области конвергенции направления
потоков сходятся.
Дивергенция - рассеивание потока масс в
ходе их перемещения по поверхности
земли. В области дивергенции направления
потоков расходятся.
Для моделирования направлений потоков в
зависимости от того, каких областей больше
(областей
дивергенции
или
областей
конвергенции)
могут
быть
применены
различные
методики
вычисления
направлений потока.

104.

105.

106.

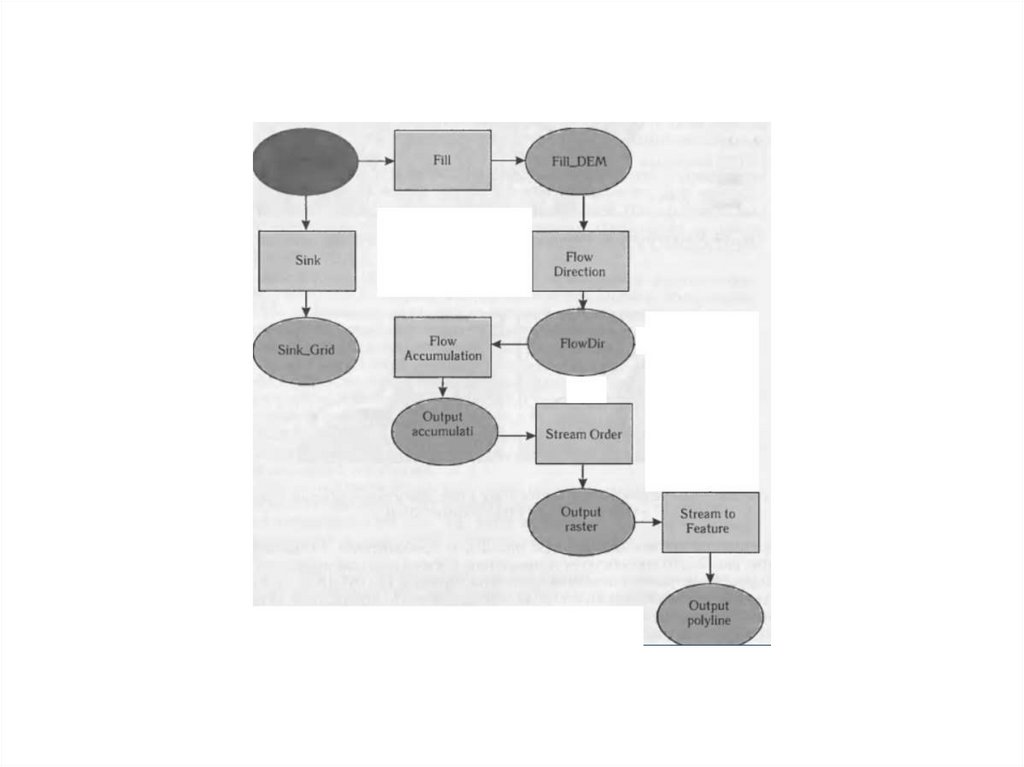
107. Все методики вычисления направления потоков делятся на: 1) те, которые позволяют рассчитать направление потока из точки (узла

сетки) в одном
направлении и 2) те, которые позволяют рассчитать направление потока
из точки в нескольких направлениях.
Так для моделирования процессов перемещения масс в области
конвергенции можно использовать те методы, которые позволяют
рассчитать направление потока из точки (узла сетки) в одном
направлении.
Для моделирования процессов перемещения масс в области дивергенции
нужно использовать те методы, которые позволяют рассчитать
направление потока из точки (узла сетки) в нескольких направлениях
направлении.
Для чего это усложнение (вычисление направление из точки в
нескольких направлениях) нужно???

108. «Single Flow direction methods» Методы рассчитывающие направление потока в одном направлении

Алгоритм – «D8». Из каждой ячейки регулярной сетки направление
потока определяется в одну из 8 соседний ячеек, которая расположена в
направлении максимального изменения функции.
305
304
307
307
308
302
300
298
299
301
299
298
296
300
301
297
296
295
294
295
1
2
3
4
5
6
7
8
9
Исходная модель рельефа
9
9
8
7
7
9
9
8
7
4
9
9
9
8
7
6
6
6
5
4
Модель с кодами
направлений
Задание направлений
Карта направлений потоков

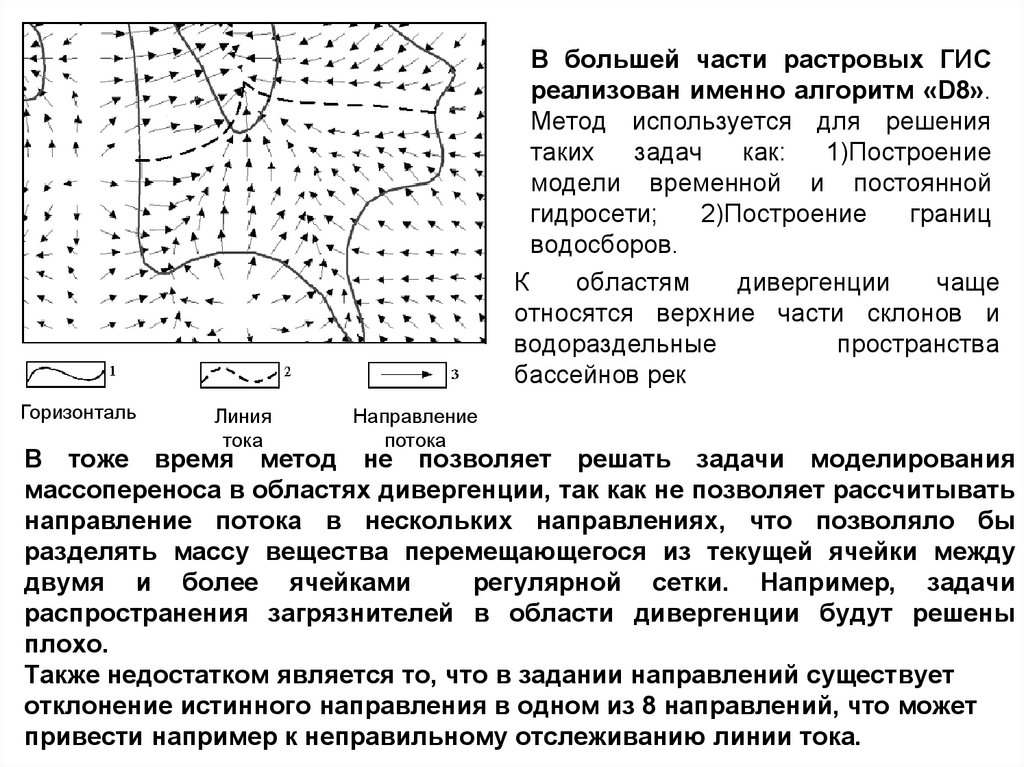
109.

В большей части растровых ГИС
реализован именно алгоритм «D8».
Метод используется для решения
таких
задач
как:
1)Построение
модели временной и постоянной
гидросети;
2)Построение
границ
водосборов.
К
областям
дивергенции
чаще
относятся верхние части склонов и
водораздельные
пространства
бассейнов рек
Горизонталь
Линия
тока
Направление
потока
В тоже время метод не позволяет решать задачи моделирования
массопереноса в областях дивергенции, так как не позволяет рассчитывать
направление потока в нескольких направлениях, что позволяло бы
разделять массу вещества перемещающегося из текущей ячейки между
двумя и более ячейками
регулярной сетки. Например, задачи
распространения загрязнителей в области дивергенции будут решены
плохо.
Также недостатком является то, что в задании направлений существует
отклонение истинного направления в одном из 8 направлений, что может
привести например к неправильному отслеживанию линии тока.

110.

Алгоритм – «Rh8». Является модификацией метода «D8», в который
вводится элемент случайности при определении направления потока, что
позволяет снизить
влияние дискретности сетки на определение
направлений. Недостатком метода является то, что он дает разные
направления потоков при многократном повторении вычисления
направления (это особенно актуально для маленьких бассейнов) .
Алгоритм – «KRA(kinematic routing algorithm)». В каждой точке
определяет направление потока исходя из величины экспозиции. Лишен
недостатка отклонения направления в одном из 8 направлений
Имея сетку экспозиций вы всегда можете сказать
куда направлен поток исходя из алгоритма KRA

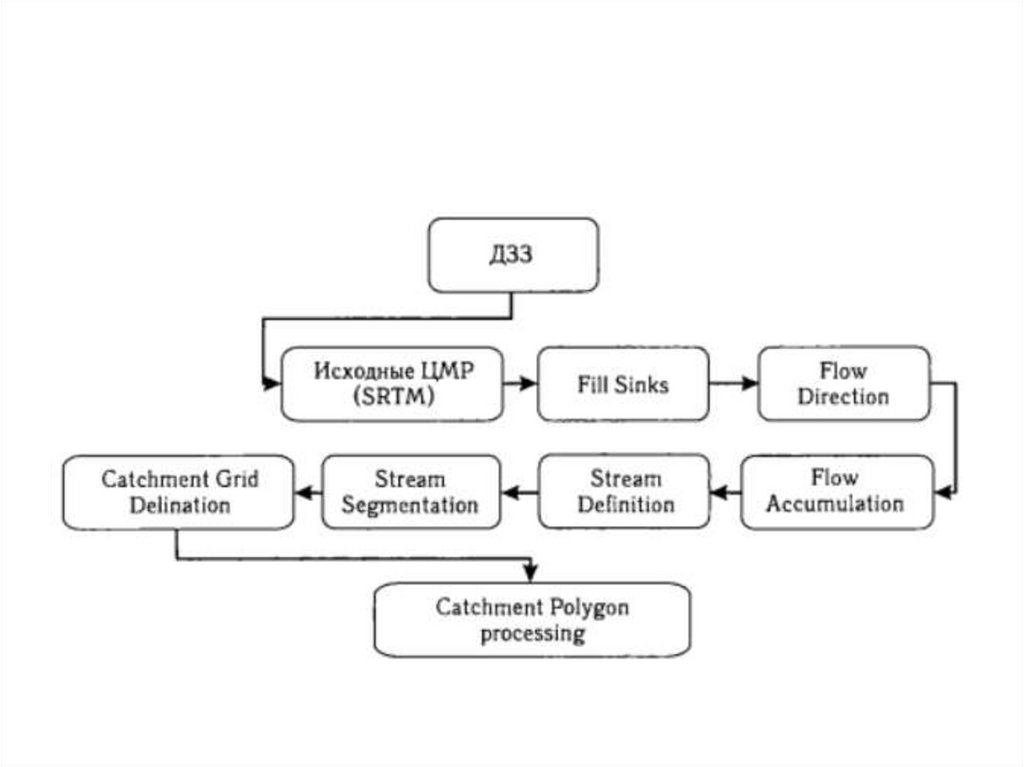
111. Водосборный бассейн (наложен на карту ЦМВ и карту временных и постоянных водотоков в TAS)

112. Алгоритмы направлений потоков

113. Локальные западины(два вида):

Западины реально существующие в рельефе (понижения, карстовые
воронки);
Артефактные западины – западины, которых нет в рельефе (ошибки
модели);
Можно их распознать и удалить только артефакты или удалить все!!!
В случае небольшого количества реально существующих западин
можно применять тотальное удаление всех западин пренебрегая
реально существующими, поскольку это не будет оказывать
существенного влияния на последующий геоинформационный анализ.
Такой подход можно применять при анализе территории имеющих
хорошее расчленение рельефа, например Татарстан, Башкирия,
Ульяновская область, территории находящиеся в горах.
В тоже время тотальное удаление недопустимо на территориях, на
которых много реально существующих западин.

114. Методы распознавания реальных западин:

• 1) согласование модели рельефа с
местностью;
• 2) согласование модели рельефа с
имеющимися в наличии топографическими
картами;
• 3) использование методов классификации;
• 4) подходы, использующие моделирование.

115. Методы удаления депрессий

1) алгоритмы заполнения западин (красная линия);
2) алгоритмы разрушения границ депрессий в направлении линий
поверхностного стока (синяя линия);
3) комбинированные методики, сочетающие два выше перечисленных
алгоритма (зеленая линия);
Разрез вдоль линий потока (черная линия исходная модель).

116.

117.

118. Области применения результатов геоморфометрического анализа

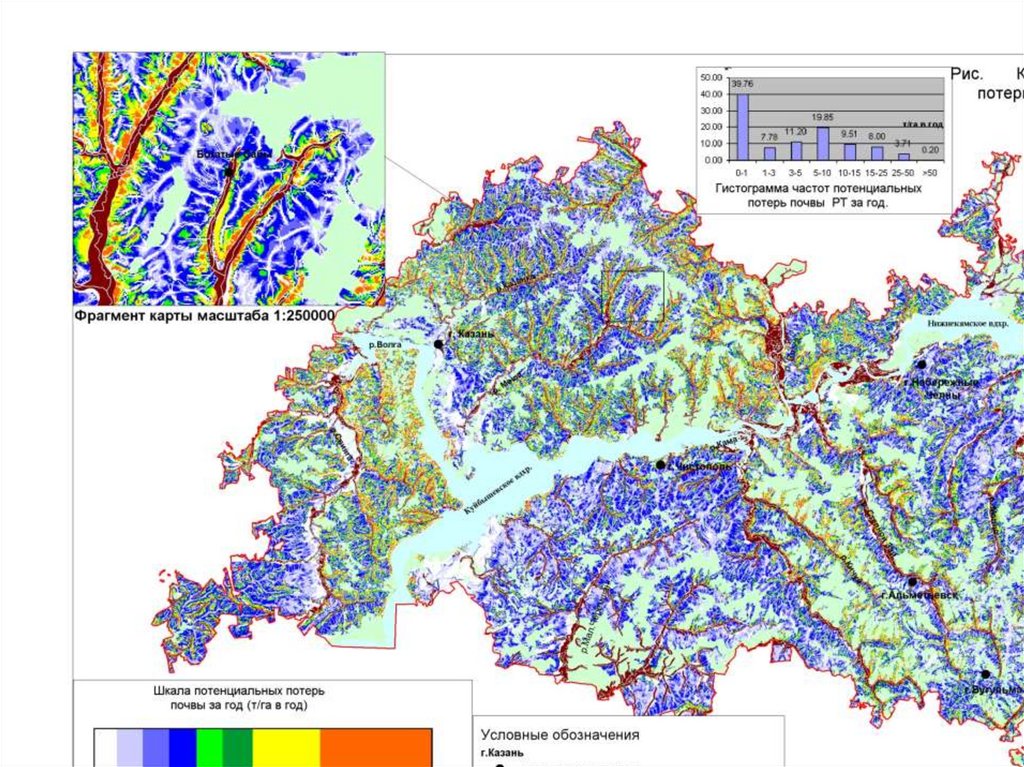
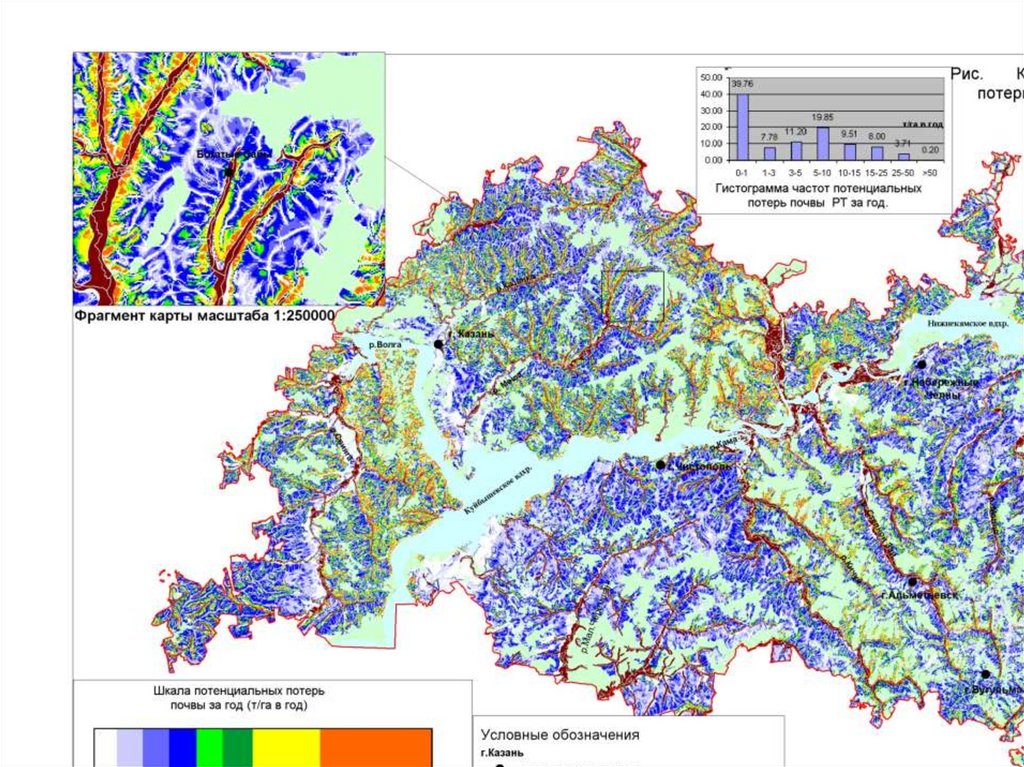
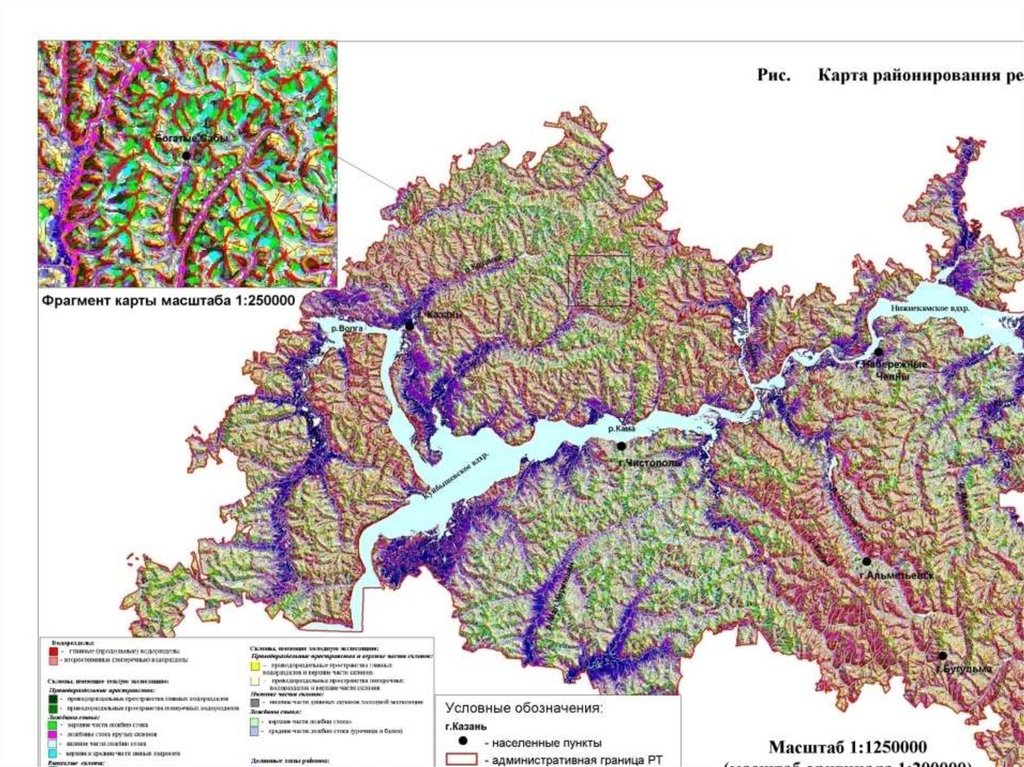
1)Морфометрическое районирование(карта типов местности);
2)Оценка потерь почвы от водной эрозии;
3)Оценка величины доставки наносов в водные объекты;
4)Оценка объемов загрязняющих веществ поступающих в
водные объекты;
5)Оценка эффективности расположения нефтеулавливающих
сооружений;
6)Построение карт зон затопления;
7)Оценка величины приходящей на изучаемую территорию
солнечной радиации;
8)Построение карт температур земной поверхности;
9)Оценка перераспределения радионуклидов антропогенного
происхождения;
10)Оценка перераспределения снежного покрова на изучаемой
территории;
11)Почвенное картографирование.

119. Оценка величины доставки взвешенных наносов в водные объекты

Взвешенными наносами называют - мелкие минеральные частицы (продукты
водной и ветровой эрозии водосборов и русел, а также абразии берегов
водоёмов), переносимые водным потоком во взвешенном состоянии.
Большая часть взвешенных наносов поступает в водоем с водосбора данного
водного объекта и в случае если поступление взвешенных наносов превышает
способность водного объекта к транспорту этого вещества происходит
заиление водоема.
Поэтому важно оценивать величину поступления взвешенных наносов в
водоемы.
Особенно это важно для непроточных водоемов и зарегулированных рек.
Поскольку у водоемов транспорт вообще отсутствует и все, что попадает в него
в нем и остается. У зарегулированных рек естественная транспортирующая
способность в зоне подпора водохранилища резко снижается, что приводит к
заполнению ложа водохранилища и русла реки в зоне подпора, что в свою
очередь ведет к увеличению площадей затопления при прохождении паводков,
уменьшению судоходных участков рек из-за сокращения глубин.

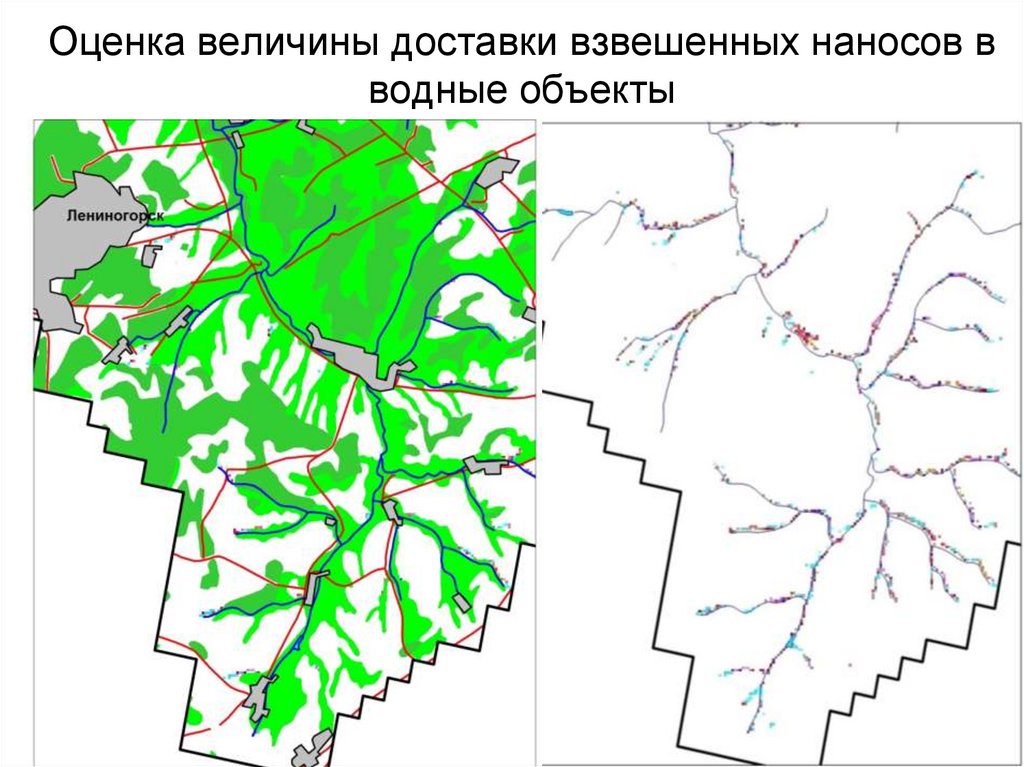
120. Оценка величины доставки взвешенных наносов в водные объекты

ГИС и геоморфометрический анализ позволяют нам выполнить такую оценку!!!
В результате оценки мы получаем карту, на которой видно в какие части реки сколько
поступает взвешенных наносов.
Для такой оценки нам необходимы следующие модели полученные на основе
растровой модели рельефа: направления потоков, уклон, плановая кривизна,
профильная кривизна. Кроме этого нужны такие растровые модели как
гидрографической сети, оврагов, лесов, дорог, населенных пунктов и лугов.
Для каждого типа землепользования(пашня, лес, луг, населенные пункты), а также для
разных типов сочетания морфометрических параметров определяется коэффициент
доставки наносов.
Коэффициент доставки наносов – это доля (в процентах) транспортирующей
способности к перемещению взвешенных наносов с исследуемой территории.

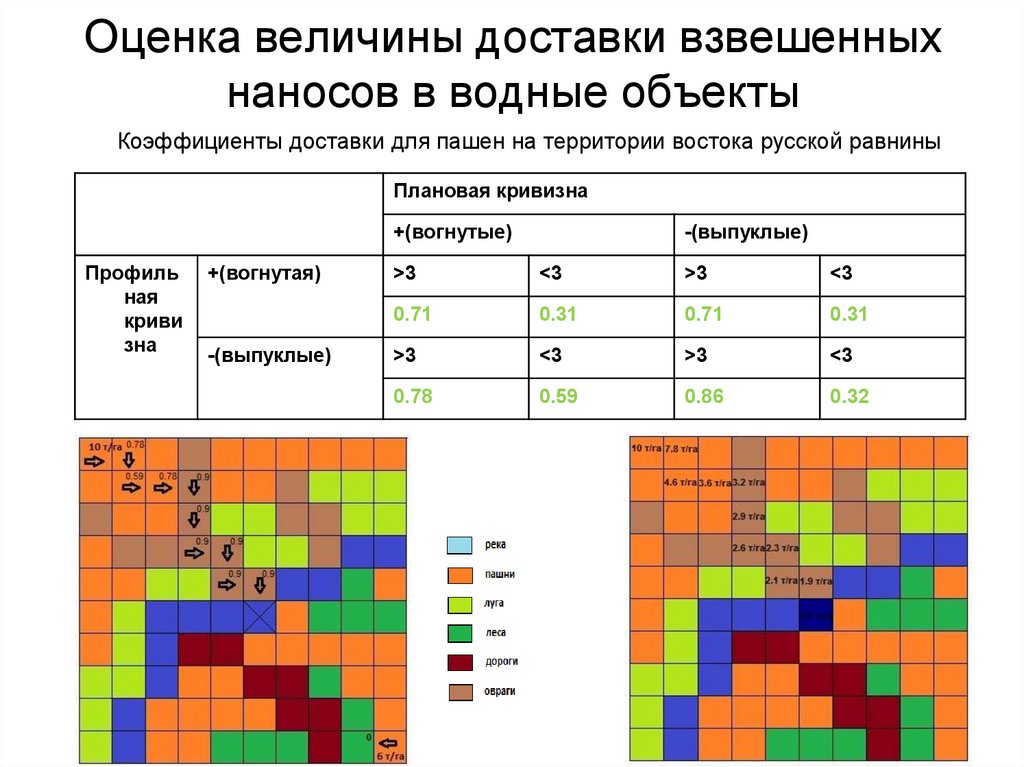
121. Оценка величины доставки взвешенных наносов в водные объекты

Коэффициенты доставки для пашен на территории востока русской равнины
Плановая кривизна
+(вогнутые)
Профиль
ная
криви
зна
+(вогнутая)
-(выпуклые)
-(выпуклые)
>3
<3
>3
<3
0.71
0.31
0.71
0.31
>3
<3
>3
<3
0.78
0.59
0.86
0.32

122. Оценка величины доставки взвешенных наносов в водные объекты

123. Оценка объемов загрязняющих веществ поступающих в водные объекты

Близкой к выше задаче оценки величины стока взвешенных наносов является
задача оценки объемов загрязняющих веществ
поступающих в водные
объекты;
Здесь речь идет об оценке объемов и концентраций веществ
адсорбирующихся на поверхности твердых частиц почвы и грунта таких
загрязнителей как тяжелые металлы и радионуклиды;
Поэтому зная величину стока взвешенных наносов в реку с водосбора мы
может в высокой степенью надежности прогнозировать величину поступающих
с водосбора тех или иных загрязняющих веществ.
Для этого нам необходима следующая исходная информация: масса
поступающих в реку взвешенных наносов и концентрация загрязнителя в водах
стекающих по рельефу.

124. Оценка расположения нефтеулавливающих сооружений.

На территориях где ведется интенсивная нефтедобывающая деятельность возможны
эксплуатационные или аварийные проливы нефтепродуктов на рельеф местности,
которые с поверхностным стоком через овражно-балочную сеть могут попасть в водные
объекты, что чрезвычайно опасно как для здоровья человека так и для водной
экосистемы.
Источники загрязнения поверхностных вод нефтепродуктами:
1. Нефтедобывающие скважины;
2. Групповые замерные установки (ГЗУ) – это установки для замера дебета скважин;
3. Нефтепроводы.
Часто в верхних звеньях овражно-балочной сети располагают нефтеулавливающие
сооружения(НУС), которые очищают воду от возможного загрязнения нефтепродуктов.
При этом при проектировании НУС необходимо оценить территорию которую будет
охватывать зона его действия и это можно сделать с использованием ГИС и
геоморфометрического анализа.

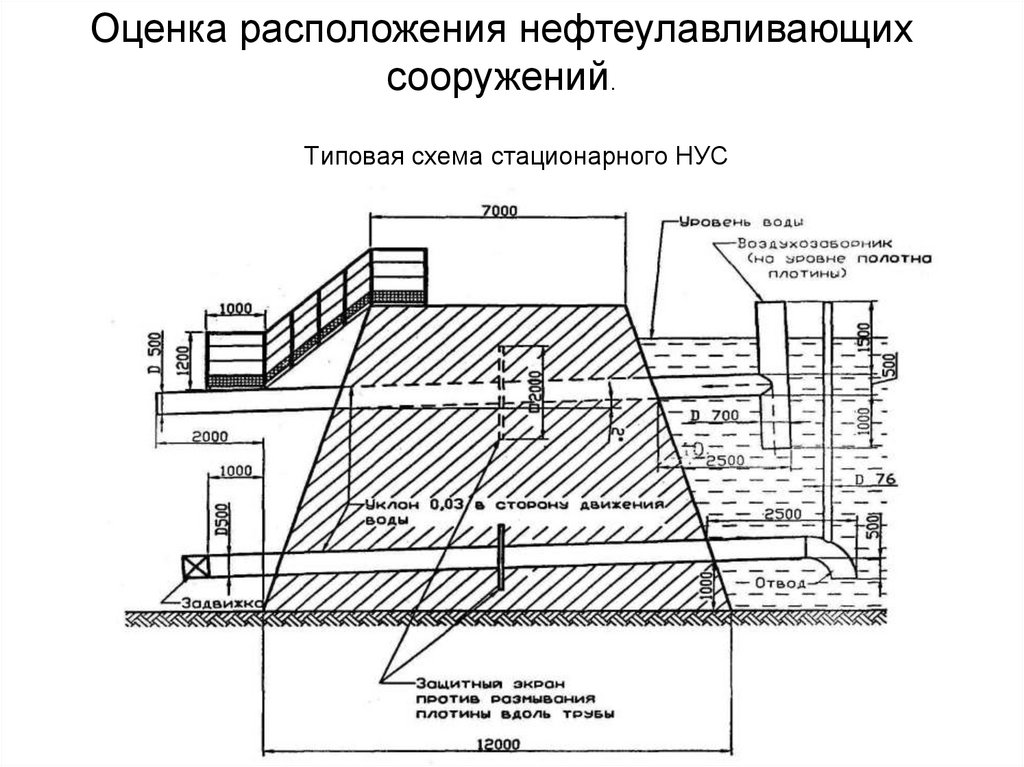
125. Типовая схема стационарного НУС

Оценка расположения нефтеулавливающих
сооружений.
Типовая схема стационарного НУС

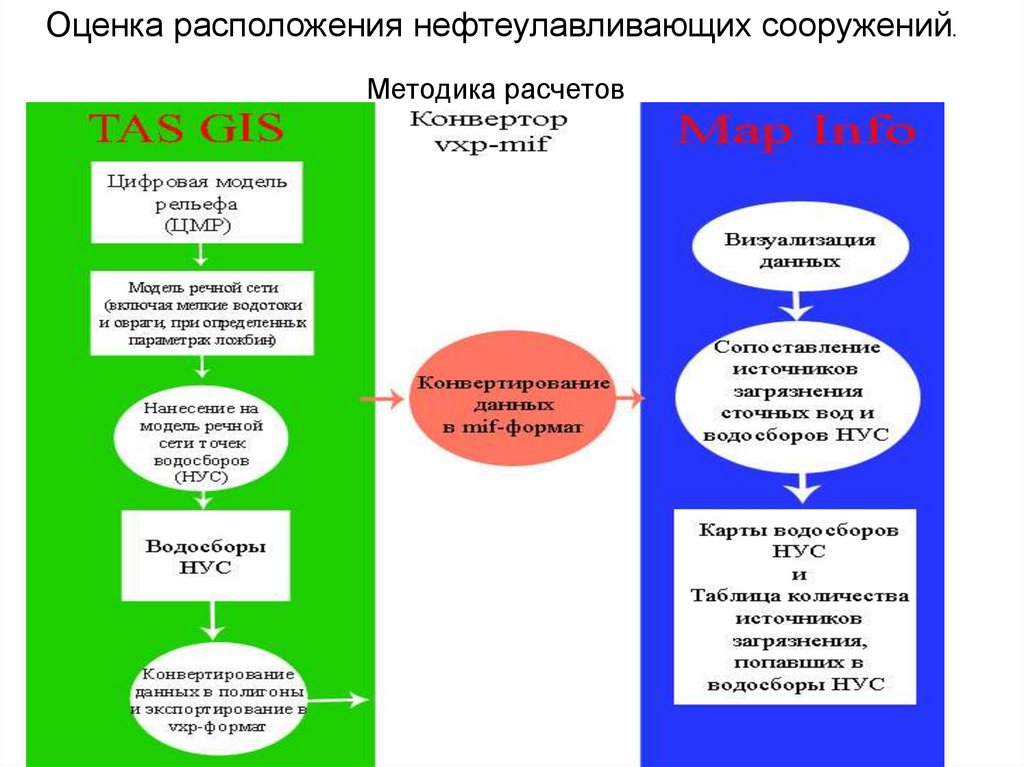
126. Методика расчетов

Оценка расположения нефтеулавливающих сооружений.
Методика расчетов

127. Карта водосборов стационарных НУС и источников загрязнения сточных вод

128. Построение карт зон затопления при прохождении весенний половодий высоких уровней обеспеченности

По данным Министерства природных ресурсов РФ
наводнения
являются одним из наиболее часто повторяющих стихийных бедствий,
охватывающие большие территории и превосходящих все другие
чрезвычайные ситуации (ЧС) по наносимому ущербу.
Среди основных причин, приводящих к большим ущербам от
половодий
в
России,
можно
назвать,
во-первых,
слабая
гидрологическая изученность и неполнота исходных данных для
осуществления достоверных прогнозов опасности затопления
территорий и их карт, во-вторых, отсутствие законодательно
закрепленных правил хозяйственного использования земель,
подверженных сезонным затоплениям.
Подобные карты зон затопления можно создать с использованием ГИС
и геоморфометрического анализа.

129. Географическая характеристика объекта исследования

Река Степной Зай – левый приток р.
Кама, одна из наиболее полноводных
малых рек на территории Республики
Татарстан, расположена в Восточном
Закамье,
юго-восточной
части
республики. Длина реки 211,3 км.
Площадь водосбора в устье 5020 км²
(7,4% территории республики).
Рис. 1. Границы
исследуемого района

130. Этапы методики:

• Построение растровой модели рельефа;
• Построение растровых моделей поверхности
уровней затопляемости различной
обеспеченности;
• Далее с использованием алгоритма алгебры
карт растровых поверхностей создаются
растровые поверхностей разностей между
моделью рельефа и моделями поверхностей
максимальных уровней воды весеннего
половодья различной
обеспеченности(например 1,2,5,10,25%).

131. 1.Построение цифровой модели рельефа

Инструмент «Topo to Raster»
в ГИС ArcGIS 10.0 предназначен
для построения гидрологически
корректной
поверхности
растровой
на
основании
векторных данных компонентов
рельефа. Метод интерполяции
основан на программе ANUDEM,
разработанная
М.
Хатчинсоном.(Исходные данные
: горизонтали, реки, озера, точки
отметок высот.)
Трехмерное отображение растровой
модели части изучаемой территории

132. 2.Методика построения карт зон затопления

Поверхности
использованием
подготовленного
точки
с
уже
построены
с
предварительно
набора
из
431
определенными
абсолютными отметками уровней
воды и превышения 1, 2, 5, 10, 25%
обеспеченности на водотоках. Для
построения сеточной поверхности
был использован метод «обратных
расстояний».
Рис. 2. Интерфейс программного
обеспечения, которое использовалось для
получения дополнительных точек

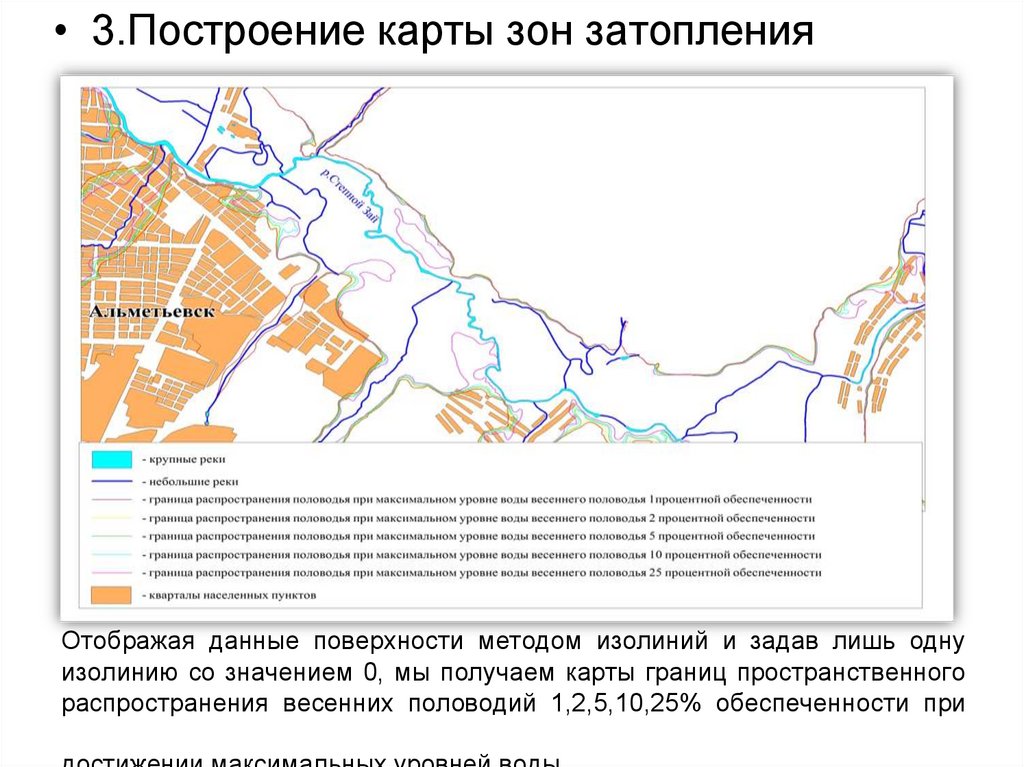
133. Отображая данные поверхности методом изолиний и задав лишь одну изолинию со значением 0, мы получаем карты границ

• 3.Построение карты зон затопления
Отображая данные поверхности методом изолиний и задав лишь одну
изолинию со значением 0, мы получаем карты границ пространственного
распространения весенних половодий 1,2,5,10,25% обеспеченности при