Similar presentations:
Истечение жидкости через отверстия и насадки. Тема 6
1.
МИНОБРНАУКИ РОССИИФедеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет
Тема 6.
Истечение жидкости через
отверстия и насадки
Санкт-Петербург 2020
Дисциплина:
Механика жидкости и газа
Преподаватель:
Феськова Алина Яновна
2.
В данном курсе рассматриваются случаи малых отверстий и тонкой стенки.y
d
При прохождении жидкости через отверстие или внутри
насадка происходит сжатие струи, то есть уменьшение
диаметра.
dсж
x
Отверстия
Насадки
При уменьшении диаметра уменьшается расход.
Отверстия могут быть различных форм: , ,
и т.д.
Насадки – это маленький кусок трубы (патрубок),
прикрепленный к отверстию (l ≤ 3÷4 d).
Виды:
– конический сходящийся;
– конический расходящийся;
– цилиндрический.
По расположению:
1) внутренние;
2) внешние.
Главная функция – позволяют увеличить расход
по сравнению с отверстиями.
3.
1. v = φ 2gH0 , где:φ – коэффициент скорости (прил. 6);
P –P
H0 – напор истечения: H0 = H + 0ρg ,
1. Скорость
истечения
(P0 – P) – разница давлений в резервуаре и снаружи,
H – напор (слой вышележащей жидкости)*.
* Если истечение происходит не
в газ, а в другую жидкость, то:
H = H 1 – H2
H1
H2
4.
2. Q = μω 2gH0 , где:2. Расход жидкости
через отверстие или
насадок.
3. Время опорожнения
μ – коэффициент расхода (прил. 6).
2W
3. tоп =
, где:
Q1
Q1 – расход жидкости через отверстие
в начальный момент времени;
W – начальный объем жидкости в
резервуаре.
5.
Типы задачПри постоянном напоре H
При переменном напоре H
∑Qвх = ∑Qвых
∑Qвх ≠ ∑Qвых
(задачи на определение tоп)
6.
Q0 d0H1
H2
Q2 d2
Q1
d1
h
Резервуар разделен тонкой стенкой, в которой
имеется круглое отверстие диаметром d0 = 30 мм.
Диаметр конически сходящегося насадка, через
который вытекает вода из первого отсека d1 = 15
мм; диаметр внешнего цилиндрического насадка,
через который вытекает вода из второго отсека d2 =
20 мм. Определить расход воды из бака Q и
глубину H2 во втором отсеке, если глубина воды в
первом отсеке H1 =1,25 м, а расстояние от дна до
центра цилиндрического насадка h = 0,2м.
Движение воды в резервуаре установившееся.
Задача 1
Дано:
Решение
d0 = 30 мм
d1 = 15 мм
d2 = 20 мм
H1 = 1,25 м
h = 0,2 м
Исходя из того, что движение установившееся, следует: Q = Q1 + Q2 и Q0 = Q2.
Q0 = Q2: распишем, чему равняется Q0 = Q2.
πd 2
Q0 = μ0ω0 2g(H1 – H2) = 0,62 0 2g(H1 – H2)
4
πd 2
Q2 = μ2ω2 2g(H2 – h) = 0,82 42 2g(H2 – h)
Уравниваем их : 0,62 ∙ d02 (H1 – H2) = 0,82 ∙ d22 (H2 – h)
Q=?
H2 = ?
Подставляем значения : 0,62 ∙ (0,03)2 (1,25 – H2) = 0,82 ∙(0,02)2 (H2 – 0,2)
Выражаем H2:
1,25 – H2
1,25 – H2
H2 – 0,2 = 0,5878; H2 – 0,2 = 0,3455; 1,25 – H2 = 0,3455 H2 – 0,0691; H2 = 0,98 м.
πd 2
π(0,015)2
Распишем и посчитаем, чему равняется Q1: μ1ω1 2gH1 = 0,94 41 2gH1 = 0,94
2 ∙ 9,81 ∙ 1,25 =
4
= 0,00082 м3/с = 0,82 л/с.
3,14 (0,02)2
Считаем Q2: Q2 = 0,82
2 ∙ 9,81 (0,98 – 0,2) = 0,001 м3/с = 1 л/с.
4
Считаем, чему равняется Q: Q = Q1 + Q2 = 0,82 +1 = 1,82 л/с.
7.
Q3H1
Q1 d1
d3
H2
Q2 d2
В бак, разделенный тонкой стенкой, поступает
вода с расходом Q = 37 л/с. В стенке и в дне
каждого отсека имеются отверстия диаметром
d1 = d2 = d3 = 10 см. Определить величины
расходов через донные отверстия, а также
рассчитать, каким должен быть диаметр d1
донного отверстия, чтобы расходы через
донные отверстия стали равны Q1 = Q2.
Движение воды в резервуаре установившееся.
Задача 2
Дано:
Решение
d1 = d2 = d3
Q = 37 л/с
Q1 = ?
Q2 = ?
Исходя из того, что движение установившееся, следует: Q = Q1 + Q2 и Q2 = Q3.
1) Q1, Q2 - ?
2)d1 (если Q1 = Q2) - ?
Распишем, чему равняется Q1 и Q2.
Q1 = μ1ω1 2gH1 ; Q2 = μ2ω2 2gH2
Выразим H2 через H1:
Смотрим на уравнение и понимаем, что H1 и H2 неизвестны
2
2
πd
πd
т.к. Q3 = Q2, то: μ3 43 2g(H1 –H2) = μ2 42 2gH2 ; (H1 –H2) = H2 ; (H1 –H2) =H2 ; H1 = 2H2 .
( μ3 = μ2 ), т.к. одинаковые отверстия. d2 = d3 по условию
Подставляем выраженное H2 в уравнение расхода :
πd 2
πd 2
Q1 = μ1 1 4gH2 ; Q2 = μ2 2 2gH2
4
4
πd2
3,14 0,12
Т.к. Q = Q1 + Q2, то: Q = μ
gH
(
4
+
2
)
=
0,65
9,8H2 (2+1,4) = 0,05 H2 ;
2
4
4
Q
0,037
H2 = 0,05 = 0,05 = 0,685; H2 = 0,469 м H1 = 2 H2 = 0,939 м
Подставляем полученные значения H1 и H2 и считаем расход:
3,14 (0,1)2
Q1 = 0,65
2 ∙ 9,8 ∙ 0,939 = 0,01547 м3/с ;
4
3,14 (0,1)2
Q2 = 0,65
2 ∙ 9,8 ∙ 0,469 = 0,01547 м3/с ;
4
Рассмотрим второй вопрос задачи: Q1 = Q2.
πd 2
πd 2
μ1 1 2gH1 = μ2 2 2gH2 ; d12 H1 =d22 H2 ;
4
4
Выразим d1 через d2:
4
4
4
4
d1 = d2 H1 / H2 = d2 H2 / 2H2 = d2 0,5 = 0,1 0,5 = 0,084 м
8.
HAA
d1
HB
d2
B
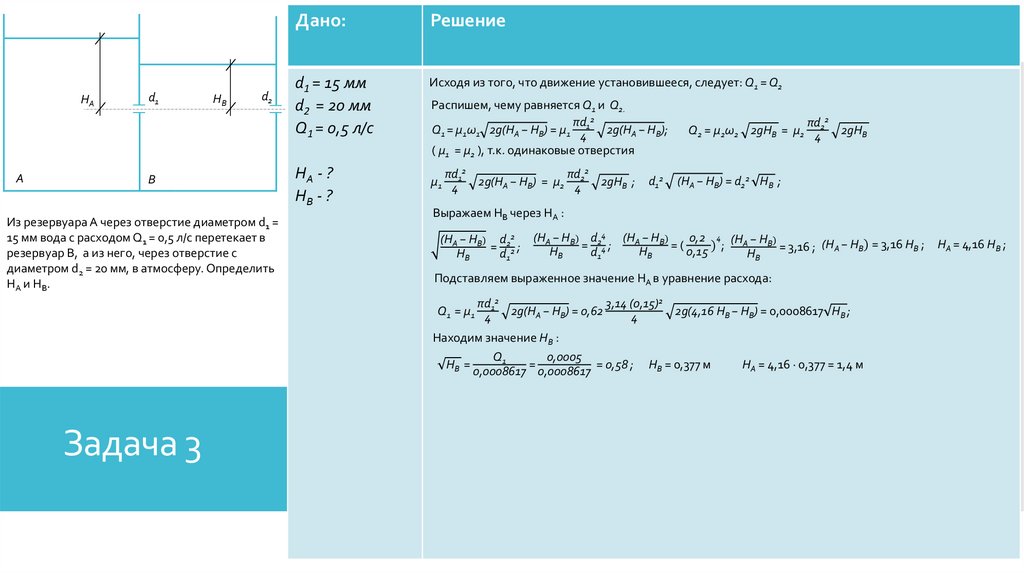
Из резервуара А через отверстие диаметром d1 =
15 мм вода с расходом Q1 = 0,5 л/с перетекает в
резервуар B, а из него, через отверстие с
диаметром d2 = 20 мм, в атмосферу. Определить
HA и Н В.
Дано:
Решение
d1 = 15 мм
d2 = 20 мм
Q1 = 0,5 л/с
Исходя из того, что движение установившееся, следует: Q1 = Q2
HA - ?
HB - ?
πd 2
πd 2
μ1 41 2g(HА − HВ) = μ2 42 2gHВ ;
Распишем, чему равняется Q1 и Q2.
πd 2
Q1 = μ1ω1 2g(HА − HВ) = μ1 1 2g(HА − HВ);
4
( μ1 = μ2 ), т.к. одинаковые отверстия
d12
πd 2
Q2 = μ2ω2 2gHВ = μ2 42 2gHВ
(HА − HВ) = d22 HВ ;
Выражаем HB через HA :
(HА − HВ) d22 (HА − HВ) = d24 ; (HА − HВ) = ( 0,2 )4 ; (HА − HВ)
(H − HВ) = 3,16 HВ ; HА = 4,16 HВ ;
= 2;
HВ
0,15
HВ
d14
HВ = 3,16 ; А
HВ
d1
Подставляем выраженное значение HA в уравнение расхода:
πd 2
3,14 (0,15)2
Q1 = μ1 41 2g(HА − HВ) = 0,62
2g(4,16 HB − HВ) = 0,0008617 HВ ;
4
Находим значение HВ :
Q1
0,0005
HВ = 0,0008617
= 0,0008617 = 0,58 ;
Задача 3
HВ = 0,377 м
HА = 4,16 ∙ 0,377 = 1,4 м
9.
PМd0
Q0
H
d1
Q1
Дано:
Решение
d1 = d0 = 20 мм
H = 1,5 м
ΔQ = 0,7 л/с
ΔQ = Q1 – Q0 , т.к. расход через внешний цилиндрический насадок больше
Pм = ?
Из закрытого резервуара вода вытекает через
круглое отверстие в тонкой стенке и внешний
цилиндрический насадок, имеющие
одинаковые диаметры d0 = d1 = 20 мм, и
находящиеся на одинаковой глубине H = 1,5 м.
Определить манометрическое давление Pм на
свободной поверхности воды, если разность
расходов отверстия и насадка ΔQ = 0,7 л/с.
Движение установившееся.
Задача 4
Распишем, чему равняется Q1 и Q0.
P
πd 2
P
Q1 = μ1ω1 2g( H + ρgм ) = 0,82 41 2g( H + ρgм );
P
πd 2
P
Q0 = μ0ω0 2g( H + ρgм ) = 0,62 40 2g( H + ρgм )
πd2
P
3,14 (0,02) 2
Pм
ΔQ = 4 2g( H + ρgм ) ( 0,82 – 0,62 ) = 3,14
19,6 ( 1,5 + 9800
) ( 0,82 – 0,62 )
4
Pм
Pм
ΔQ = 0,000314 ∙ 4,427 ( 1,5 + 9800
) ∙ 0,2 = 0,000278 ( 1,5 + 9800
)
Pм
ΔQ
0,0007
( 1,5 + 9800
) = 0,000278 = 0,000278 = 2,518
Pм
1,5 + 9800
= 6,34
Pм = 47434,47 Па








 physics
physics Construction
Construction