Определение смежных углов

1.

2.

Познакомиться
с определением смежных углов,
с теоремой о смежных углах и ее
доказательством,
со следствиями из теоремы о смежных углах,
с видами углов.
Научиться решать задачи по данной теме.

3.

В
С
.О
А
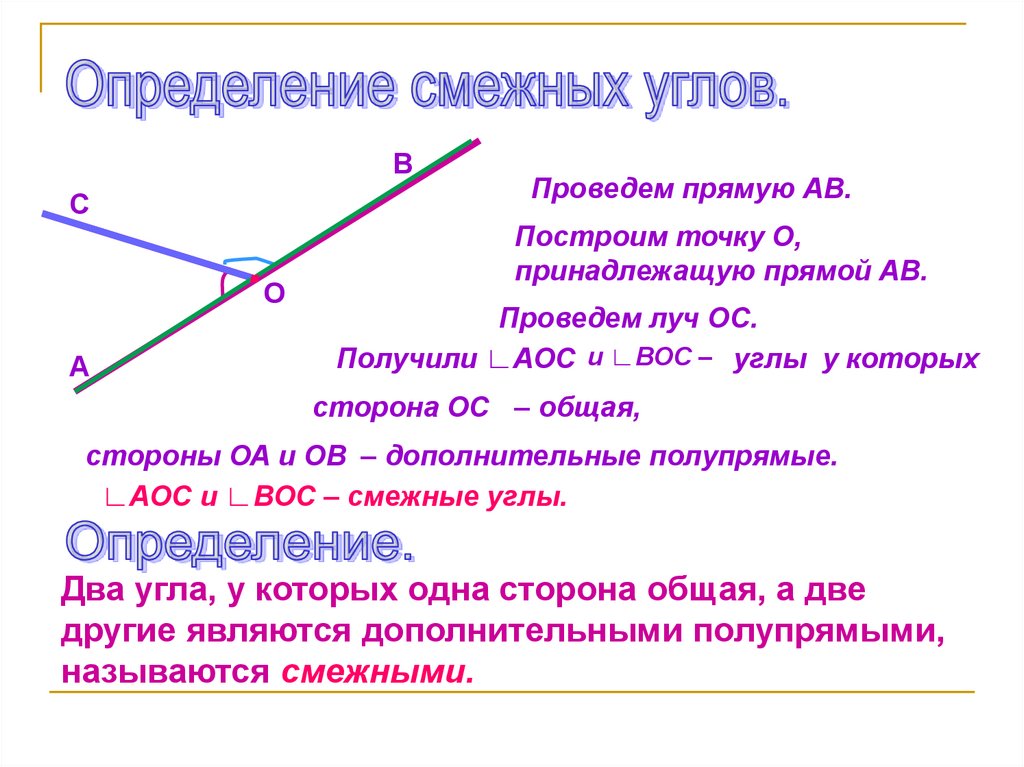
Проведем прямую АВ.
Построим точку О,
принадлежащую прямой АВ.
Проведем луч ОС.
Получили ∟АОС и ∟ВОС – углы у которых
сторона ОС – общая,
стороны ОА и ОВ – дополнительные полупрямые.
∟АОС и ∟ВОС – смежные углы.
Два угла, у которых одна сторона общая, а две
другие являются дополнительными полупрямыми,
называются смежными.

4.

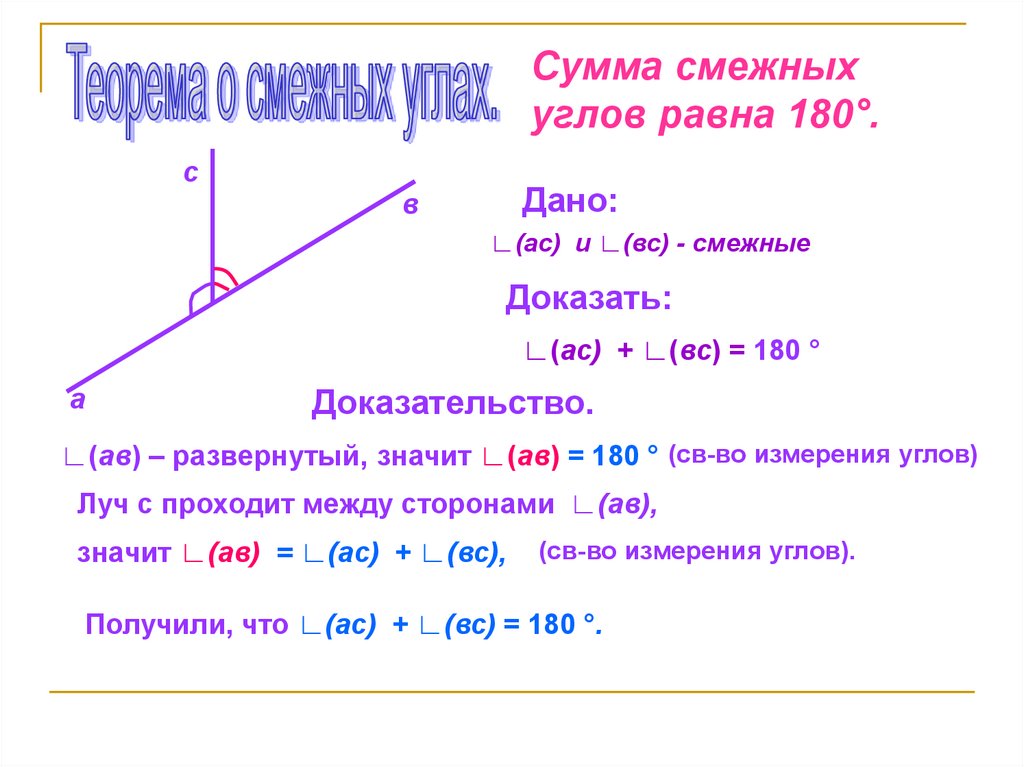
Сумма смежных
углов равна 180°.
с
Дано:
в
∟(ас) и ∟(вс) - смежные
Доказать:
∟(ас) + ∟(вс) = 180 °
а
Доказательство.
∟(ав) – развернутый, значит ∟(ав) = 180 ° (св-во измерения углов)
Луч с проходит между сторонами ∟(ав),
значит ∟(ав) = ∟(ас) + ∟(вс),
(св-во измерения углов).
Получили, что ∟(ас) + ∟(вс) = 180 °.

5.

3
4
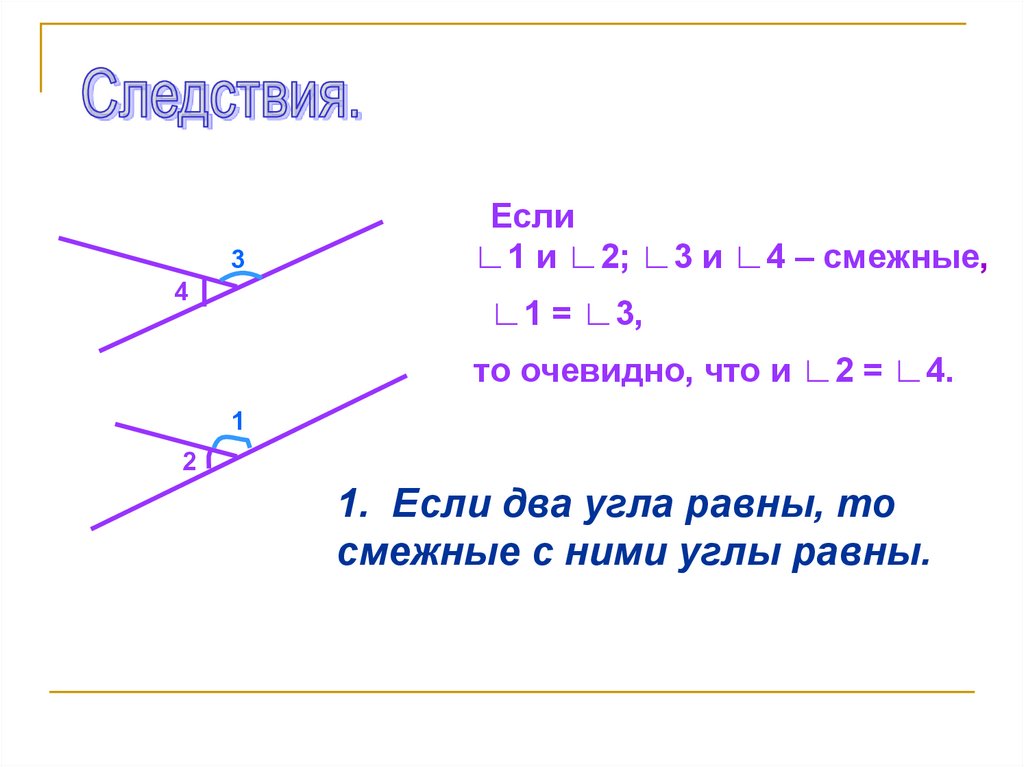
Если
∟1 и ∟2; ∟3 и ∟4 – смежные,
∟1 = ∟3,
то очевидно, что и ∟2 = ∟4.
1
2
1. Если два угла равны, то
смежные с ними углы равны.

6.

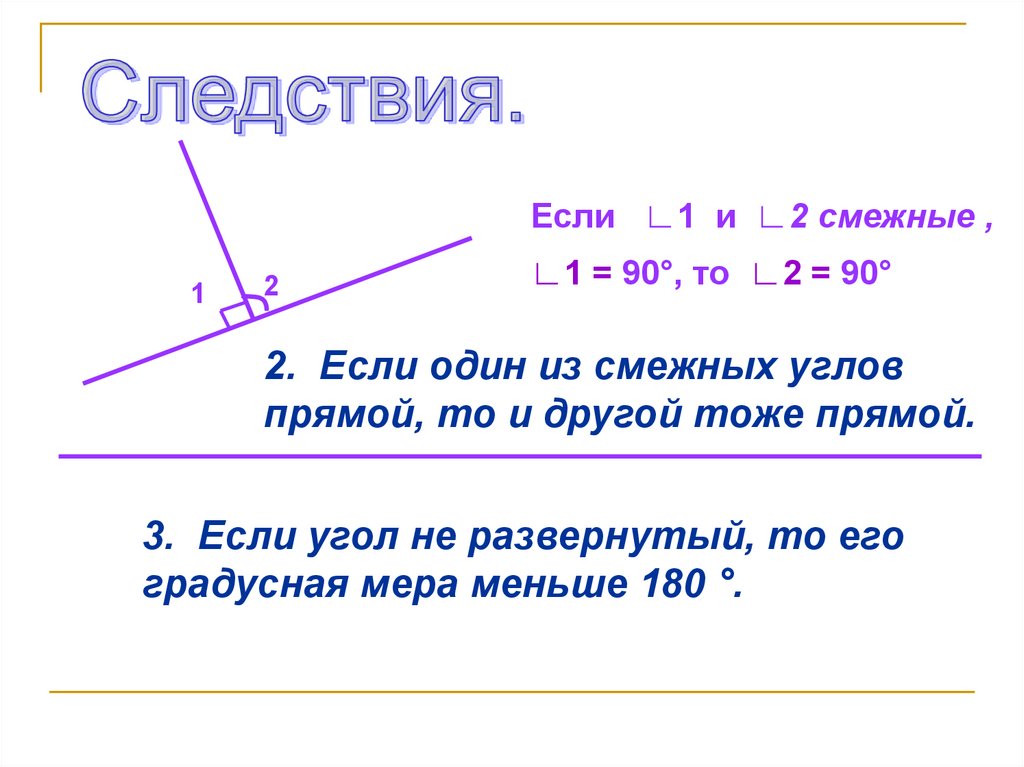
Если ∟1 и ∟2 смежные ,
1
2
∟1 = 90°, то ∟2 = 90°
2. Если один из смежных углов
прямой, то и другой тоже прямой.
3. Если угол не развернутый, то его
градусная мера меньше 180 °.

7.

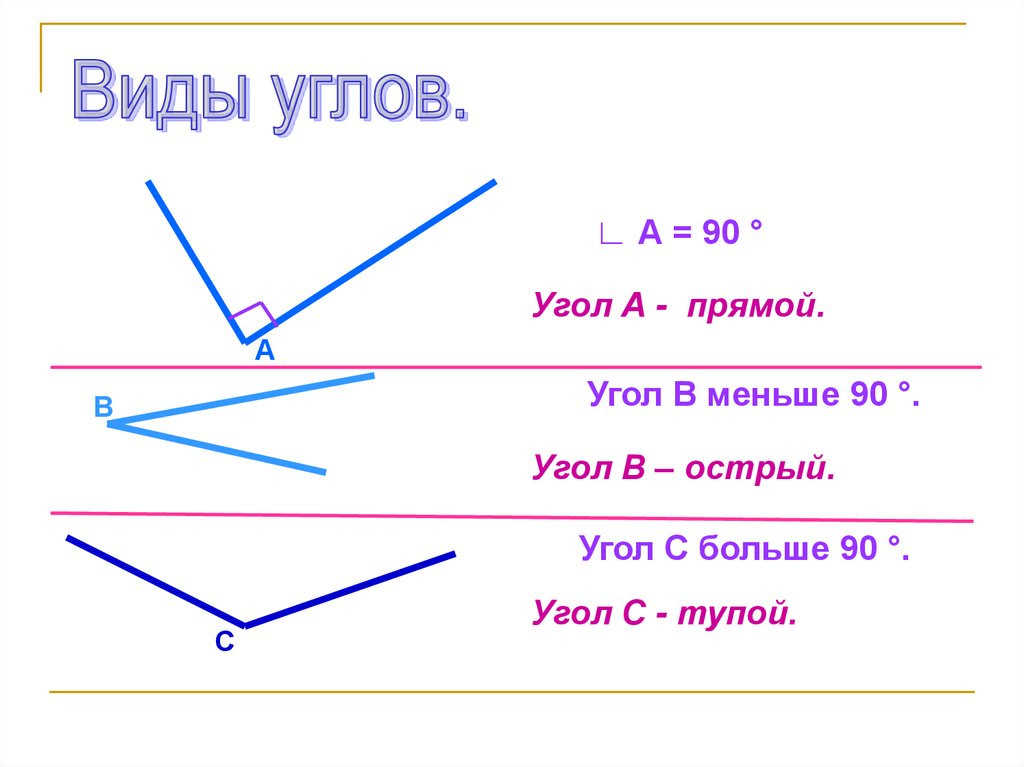
∟ А = 90 °
Угол А - прямой.
А
Угол В меньше 90 °.
В
Угол В – острый.
Угол С больше 90 °.
С
Угол С - тупой.

8.

Найти смежные углы, если один из
них в 4 раза меньше другого.
2
1
Дано:
∟1 и ∟ 2- смежные
∟1 в 4 раза меньше ∟2.
Найти:
∟1 и ∟ 2.
Решение.
Пусть ∟1 = х °, тогда ∟2 =( 4х ) °.
∟1 + ∟2 = 180 °, (по теореме о смежных углах).
Составим уравнение:
х+ 4х = 180
5х = 180
∟1 = 36 °
х = 36
1) ∟2 = 36∙ 4 = 144°
Ответ: 36 °, 144 °

9.

1.Знать теорему о смежных углах, ее
доказательства и следствия из теоремы, (п. 14)
2. №2 (устно), № 4 ( 1, 2, 4), стр.30.
Оценки за урок: