Дискретные модели данных в компьютере. Представление чисел

1. ДИСКРЕТНЫЕ МОДЕЛИ ДАННЫХ В КОМПЬЮТЕРЕ. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ

14.12.2023

2. Цель урока:

Знакомство с представлением чисел
в памяти компьютера.
14.12.2023

3. Главные правила представления данных в компьютере

1. Данные и программы в памяти компьютера
хранятся в двоичном виде.
2. Представление данных в компьютере дискретно.
3. Множество представимых в памяти величин
ограничено и конечно.
4. В памяти компьютера числа хранятся в двоичной
системе счисления.

4.

• Любая информация в памяти компьютера
представляется с помощью нулей и единиц, то
есть с помощью двоичной системы счисления.
Первоначально компьютеры могли работать
только с числами. Теперь это и числа, и
тексты, и изображение, и звук.
• Работа с данными любого типа сводится к
обработке двоичных чисел – чисел,
записываемых с помощью двух цифр – 0 и 1.
• В компьютере различаются два типа числовых
величин: целые числа и вещественные
(действительные) числа. Различаются способы
представления их в памяти компьютера.

5.

Часть памяти, в которой хранится
одно число, называется ячейка.
Минимальный размер ячейки, в
которой может храниться целое
число, - 8 битов, или 1 байт.

6. Представим число 15 в памяти компьютера. Для этого мы должны перевести его в двоичную систему счисления.

0
0
0
0
1
1
1
1
Мы получили внутреннее представление числа.
14.12.2023

7. Вспомним из 9 класса Алгоритм перевода десятичного числа в двоичное число

1. Последовательно делить «в столбик»
исходное десятичное число и получаемые
частные на 2 до тех пор, пока частное не
станет равным 1.
2. Полученные остатки от деления (это будут 0
или 1) записать справа налево, начиная с
последнего частного. Это и будет значение
числа в двоичной системе.

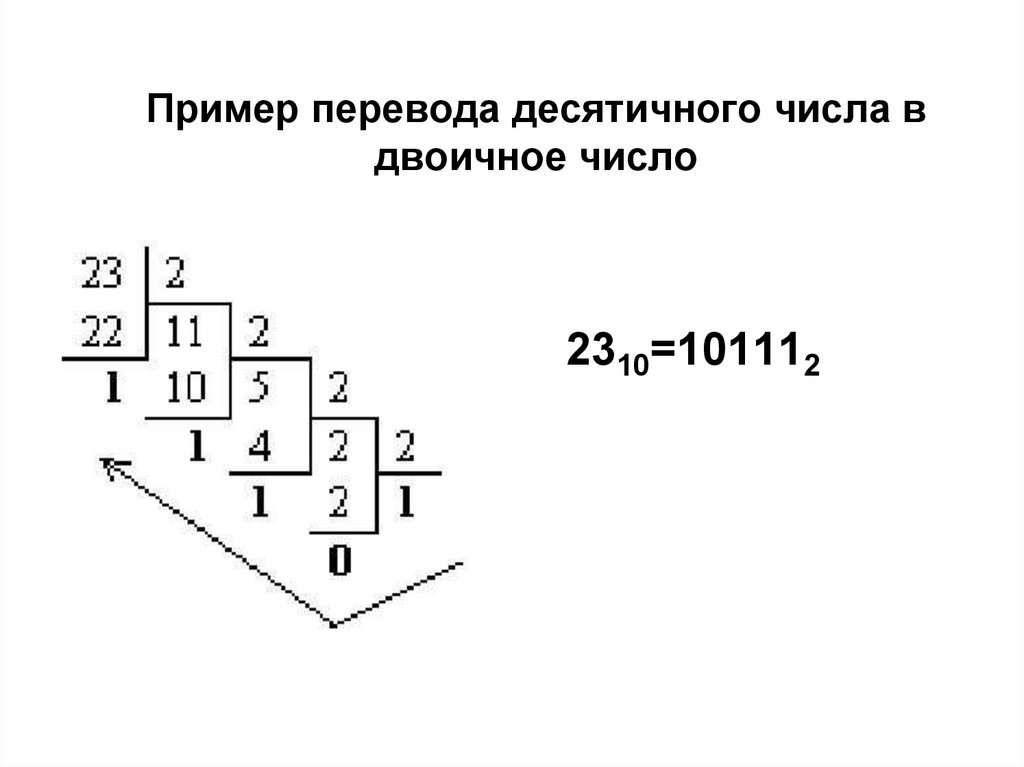
8. Пример перевода десятичного числа в двоичное число

2310=101112

9. Сложение двоичных чисел

Таблица сложения:
0+0=0
1
0
0+1=1 +
1
1+0=1
1 + 1 = 10
11
1
11
+
1
100

10.

Алгоритм представления
отрицательных целых чисел в
компьютере
1. Перевести модуль данного
отрицательного числа в двоичную
систему счисления.
2. Дописать впереди нули, заполнив всю
разрядную сетку (прямой код).
3. Заменить нули на единицы, а единицы
на нули (инвертировать) (обратный код).
4. К полученному числу в столбик
прибавить 1 (дополнительный код).
14.12.2023

11. Определим внутреннее представление числа -1510 в восьмиразрядной сетке.

Запишем внутреннее представление числа
1510 – 00001111 (переведем в двоичную
систему и добавим впереди нули до 8
разрядов)
Запишем обратный код – 11110000
К полученному числу прибавим 1 – 11110001
1
14.12.2023
1
1
1
0
0
0
1
Первый бит указывает на знак числа. Если
он = 0, то число положительное, если = 1, то
число отрицательное.

12. Разряд и диапазон ячеек

• В восьмиразрядной ячейке можно
получить числа диапазоном
-128<=X<=127.
• В 16-рядной ячейке можно получить
числа диапазоном
-32768<=X<=32767
• В 32-разрядной ячейке можно получить
числа диапазоном
-2147483648<=X<=2147483647
В общем виде:
14.12.2023
-2N-1<=X<=2N-1-1

13.

Пример 1. Определить прямой, обратный и дополнительный коды следующих двоичных
чисел:
а)100100; б) -100011; в) -100100.
Решение
Будем считать, что число размещается в двух байтах. Старший бит – знак разряда.
Незначащие нули добавляются слева от числа. Результат представим в виде таблицы:
Прямой код
Обратный код
Дополнительный
код
100100
0000000000100100
0000000000100100
0000000000100100
-100011
1000000000100011
1111111111011100
1111111111011101
-100100
1000000000100100
1111111111011011
1111111111011100
Число
Пример 2. Как будет представлено в памяти компьютера целое число 12345 10 ?
Решение
Для размещения числа возьмем два байта.
Поскольку число положительное, то в старшем (15-м) бите будет 0.
Переведем число в двоичную систему счисления:
1234510 = 110000001110012.
Результат:
0
0110000
Знак числа
00111001
число
13

14.

Домашнее задание
Прочитать параграф 19 и письменно выполнить задания:
1.Запишите внутреннее
8-разрядную ячейку:
а) 64
б) -58
представление
в) 37
2. Запишите внутреннее
16-разрядную ячейку:
а) 25
б) -25
десятичных
чисел,
используя
чисел,
используя
г) -96
представление
в) 84
десятичных
г) -62
Примечание: Положительные числа достаточно перевести в двоичную систему
счисления и дописать впереди нули до 8 или до 16 разрядов. Для отрицательных
чисел нужно выполнить все 4 пункта алгоритма (он представлен выше в
презентации).
14