Similar presentations:
Плавучесть. Лекция № 4
1. ПЛАВУЧЕСТЬ
2.
Плавучестью называется способность судна плавать неопределеннуюватерлинию, неся на себе все грузы, положенные по роду службы.
На плавающее судно действуют следующие силы:
1) Силы веса всех составных частей судна и всех грузов, находящихся
на нем. Равнодействующая этих сил, обозначаемая P , измеряется в тоннах и
называется весом судна; она направлена по вертикали вниз и приложена в
точке G , называемой ц е н т р о м т я ж е с т и судна (ЦТ).
2) Силы гидростатического давления воды на смоченную поверхность
судна. Равнодействующая этих сил, обозначаемая D , называется с и л о й
п о д д е р ж а н и я (силой плавучести), и измеряется в Н. Эта сила направлена
по вертикали вверх и приложена в центре тяжести подводного объема судна.
Эту точку называют ц е н т р о м в е л и ч и н ы (ЦВ) и обозначают буквой C .
3.
Сила поддержания, согласно закону Архимеда, равна весу вытесняемого судном объема воды, т. е.D V ,
где
V - подводный объем, называемый об ъ е м 3
н ы м в од о из м е щ е н ием , измеряется в м ;
- объемный вес воды (кН/м 3), равный 1,000
для пресной воды и принимаемый равным 1,025
для морской воды. В действительности объемный вес воды в разных морях различен.
Вес воды в объеме V , равный D , называется
в е с о вы м в од о изм ещ е н ие м .
4.
Грузоподъемность и грузовместимость нетто связаны следующимисоотношениями:
G
Vн
G н
(28)
pн
где
p н - удельный погрузочный вес груза в Н/м3,
н - удельный погрузочный объем грузов в м3/Н.
5.
УСЛОВИЯ И УРАВНЕНИЯ РАВНОВЕСИЯ СУДНАДля плавания судна в равновесном положении по определенную
заданную ватерлинию необходимо и достаточно, чтобы:
1) вес судна равнялся весовому водоизмещению,
2) ЦТ судна и ЦВ лежали на одной вертикали. Аналитически это
выражается в общем случае следующими зависимостями:
(36)
P D V
xc xg
tg
(37)
zg zc
yc yg
zg zc
tg ,
(38)
где
x g , yg ,zg - координаты ЦТ судна;
x c , y c , z c - координаты ЦВ;
- угол продольного наклонения (дифферента);
- угол поперечного наклонения (крена).
В частных случаях посадки судна последние два выражения меняются, тогда
как первое всегда сохраняется.
6.
1) Если судно сидит прямоxc xg
tg ; yc yg 0 .
zg zc
2) Если судно сидит на ровный киль
yc yg
xc xg ;
tg .
zg zc
3) Если судно сидит прямо и на ровный киль
x c x g yc yg 0
7.
ВЫЧИСЛЕНИЕ ВЕСА СУДНА И КООРДИНАТ ЕГО ЦТВес судна P и координаты его ЦТ вычисляют в таблице нагрузки,
суммируя веса всех частей, входящих в состав судна, и статические моменты
их относительно плоскостей проекции.
Искомые расчетные формулы:
Вес судна
P pi .
(39)
Абсцисса ЦТ
pi x i
.
(40)
xg
P
Ордината ЦТ по высоте
pi z i
zg
.
(41)
P
8.
. ЭЛЕМЕНТЫ ШПАНГОУТОВ И ВАТЕРЛИНИЙПри вычислении элементов шпангоутов и ватерлиний удобно
нумеровать шпангоуты считая от миделя в нос и в корму, а ватерлинии вверх от основной плоскости. Нумера шпангоутов далее будем обозначать
i 0,1,2...m , а нумера ватерлиний j 0,1,2...k .
L
Расстояние между шпангоутами L
.
2m
T
Расстояние между ватерлиниями T .
k
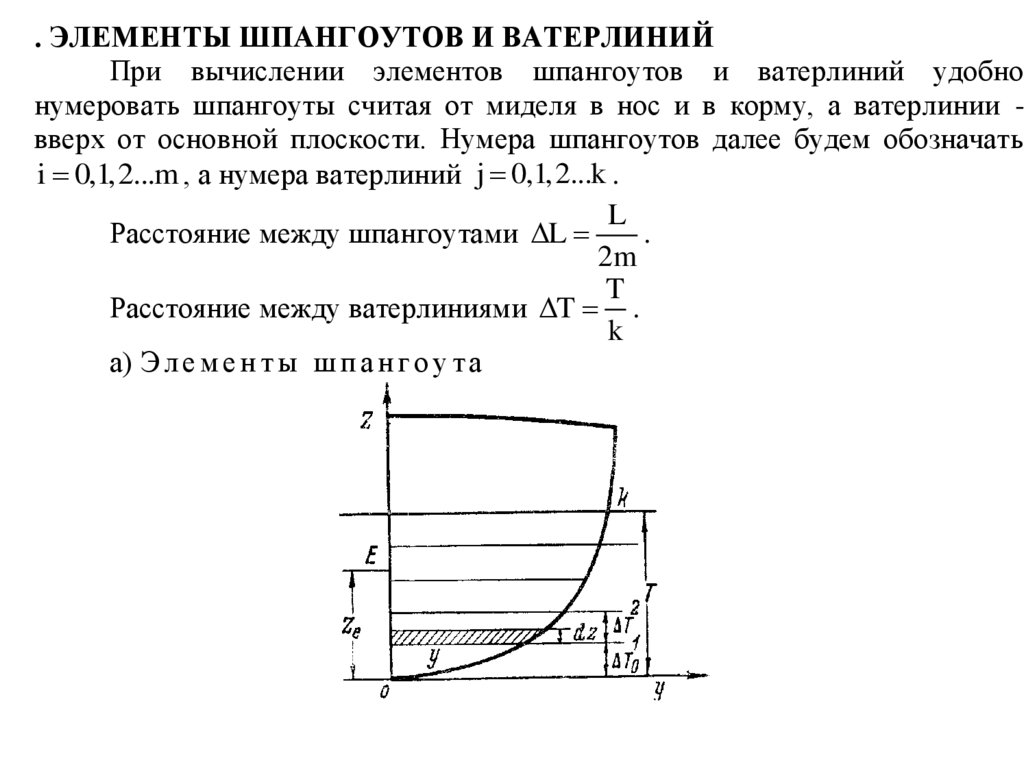
а) Э л е м е н т ы ш п а н г о у т а
9.
Погруженная площадь шпангоутаT
i 2 ydz
(44)
0
Ордината ЦТ площади
T
zydz
z e 0T
(45)
ydz
0
абсцисса ЦТ площади ye 0 ввиду симметрии.
Соответствующие расчетные формулы
(применительно к формулам 9):
k
i 2 T y j
j 0
по
правилу
трапеций
k
jy
z e T i 0k
j
1
y
i 0
j
.
(46)
10.
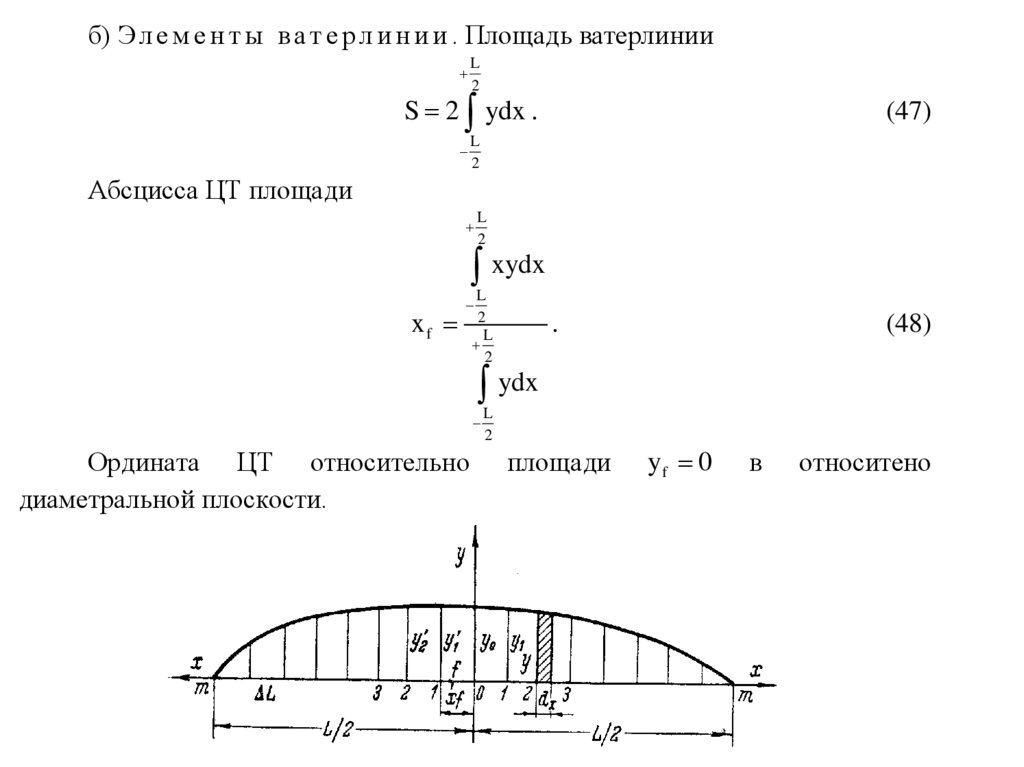
б) Э л е м е н т ы в а т е р л и н и и . Площадь ватерлинииL
2
S 2 ydx .
(47)
L
2
Абсцисса ЦТ площади
L
2
xydx
xf
L
2
L
2
.
(48)
ydx
Ордината ЦТ относительно
диаметральной плоскости.
L
2
площади
yf 0
в
относитено
11.
Моменты инерцииIx
L
2
2
3
y
dx
3 L
(49)
2
L
2
I y 2 x 2 ydx .
(50)
L
2
Соответствующе расчетные формулы по
(применительно к формулам 10 и 14):
m
S 2 L yi y i
i 0
правилу
трапеции
(51)
m
xf L
i y y
i 0
m
i
i
1
y y
i 0
i
i
2
m 3
I x L yi y i 3 a
3
i 0
m 2
I y 2 L i yi y i b .
i 0
(52)
(54)
(53)
12.
Расчетные формулы по правилу Чебышева (применительно к формулам11 и 16);
L n
S 2 yi
(55)
n i 1
n
xf
ky
L
2
i 1
n
i i
y
i 1
(56)
i
2L n 3
Ix
yi
3 n i 1
(57)
2 n
L L
I y 2 k i2 yi .
n 2 i 1
(58)
13.
ВЫЧИСЛЕНИЕ ВОДОИЗМЕЩЕНИЯВычисление водоизмещения сводится по существу к операции
двукратного интегрирования.
Объемное водоизмещение можно выразить следующим определенным
интегралом
L
2
V dx ,
(59)
L
2
где - площади погруженных частей шпангоутов в зависимости от х-ов,
т.е. от положения шпангоутов по длине судна.
Площади в свою очередь могут быть выражены интегралами, как это
отмечено в предыдущем параграфе, т.е. по формуле (44)
T
2 ydz
0
Подставляя это выражение в формулу (59), получим окончательно
выражение для объемного водоизмещения:
L
2 T
V 2 ydzdx ,
L 0
2
(60)
14.
Если взять в качестве исходных данных заданные площади ватерлиний, тодля объемного водоизмещения будем иметь:
T
V Sdz .
(61)
0
В свою очередь площади ватерлиний S (как это было приведено в
предыдущем параграфе), можно выразить по формуле (47), т.е.
L
2
S 2 ydx .
L
2
Подставляя это выражение в формулу (61), имеем для объемного
водоизмещения
T
L
2
V 2 ydxdz ,
(62)
0 L
2
т.е. снова формулу двукратного интегрирования, которая отличается от
вышеприведенной формулы (60) лишь порядком интегрирования.
15.
Расчетные формулы имеют следующий вид:а) П о п р а в и л у т р а п е ц и й для площади шпангоута (формула 46)
T
k
i 2 ydz 2 T y j
j 0
i
0
или, обозначая для краткости через i выражение в скобках, имеем:
i 2 T i .
(63)
Далее, переходя к формуле (59), будем иметь для объемного
водоизмещения
L
2
m
V dx L i i u
i 0
L
(64)
2
или, вводя предыдущее обозначение
m
V 2 T L i i u1 ,
i 0
где - обозначает также исправленные суммы по правилу трапеций.
(65)
16.
б) П о с м е ш а н н о м у с п о с о б у . Применяя правило Чебышева кформуле (59), будем иметь:
L
2
L m
V dx i ,
n i 1
L
(69)
2
а для вычисления площадей шпангоутов применим правило трапеций, т.е. по
формуле (46):
T
k
i 2 ydz 2 T y j .
j 0
i
0
Подставляя в предыдущую формулу, получаем:
L n k
V 2 T y j .
(70)
n i 1 j 0
i
17.
ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВКоординаты ЦВ ( x c и z c ) обычно вычисляют, пользуясь результатами
предыдущих вычислений в таблице водоизмещения. Таким образом, можно
считать, что известны площади шпангоутов i и площади ватерлиний S j или
величины им пропорциональные i и w j . Исходя из этого, для вычисления
искомых координат будем иметь следующие формулы:
Абсцисса ЦВ
L
2
x dx
xc
L
2
L
2
dx
L
2
.
(71)
18.
а) П о п р а в и л у т р а п е ц и йm
i a
i
x c L i m0
i
i
(72)
u
i
i 0
i
или
m
x c L
i b
i
i 0
m
i
b
i
i 0
1
,
(73)
i
где a 1 ; u ; b1 и b - поправки, как полусуммы крайних членов.
б) П о п р а в и л у Ч е б ы ш е в а
n
k i i
L
x c i 1n
2
i
(74)
i 1
или
n
xc
k
L
2
i 1
n
i
i 1
i
i
.
(75)
19.
Ордината ЦВ по высотеT
zSdz
z c 0T
(76)
Sdz
0
Соответствующая расчетная формула по правилу трапеций:
k
jS e
j
z c T j k0
(77)
S
j 0
j
или
k
jw e
j
z c T j k0
1
w
j 0
j
1
(78)
20.
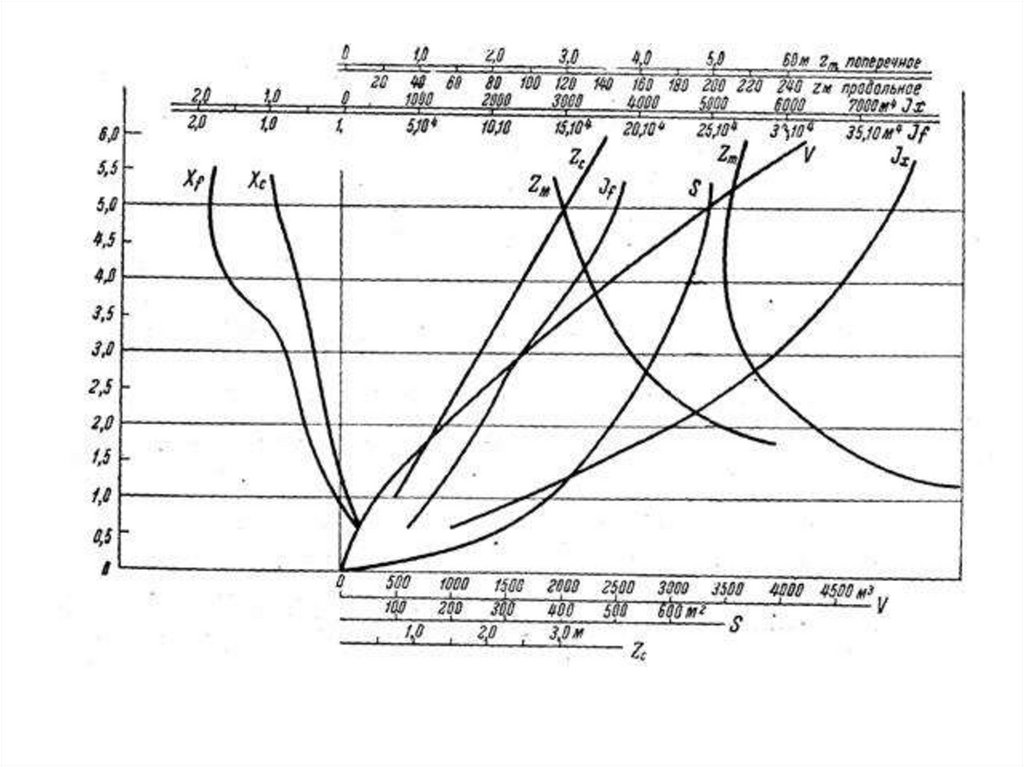
КРИВЫЕ ЭЛЕМЕНТОВ ТЕОРЕТИЧЕСКОГО ЧЕРТЕЖАПользуясь теоретическим чертежом для судна, сидящего прямо и на
ровный киль, строят следующие кривые в функции осадки:
1) S f z - строевая по ватерлиниям, выражающая зависимость
площадей ватерлиний от осадки. Площадь этой кривой, по определенную
осадку z T , выражает, в соответствующем масштабе, водоизмещение судна
для осадки T . Далее, ордината ЦТ этой площади выражает в масштабе
ординату ЦВ z c . Наконец, коэффициент полноты площади, ограниченной
этой строевой, равен коэффициенту вертикальной полноты .
2) V z - грузовой размер - кривая, выражающая зависимость
объемного водоизмещения от осадки. Грузовой размер является
интегральной кривой строевой по ватерлиниям.
3) x f f z - кривая абсцисс ЦТ площадей ватерлиний в зависимости
от осадки.
4) x c f z - кривая абсцисс ЦВ в зависимости от осадки.
5) zc f z - кривая ординат ЦВ в зависимости от осадки.
6) I x f z - кривые главных центральных моментов
7) I y f z - инерции площадей ватерлиний в зависимости от осадки.
21.
22.
строится кривая f x , называемая с т р о е в о й по шпангоутам (рис.19), ординаты которой выражают, в масштабе, величины погруженных
площадей шпангоутов в зависимости от положения последних по длине
судна.
Рис. 19.
Площадь, ограниченная этой кривой, выражает, в соответствующем
масштабе, объемное водоизмещение судна, а абсцисса ЦТ этой площади
выражает, в масштабе, абсциссу ЦВ x c . Наконец, коэффициент полноты
площади, ограниченной этой строевой, равен коэффициенту
(коэффициенту продольной полноты судна).
23.
На грузовой шкале наносят одновременно: осадки, водоизмещения,грузоподъемность или дейдвейт и высоту надводного борта
24.
ИЗМЕНЕНИЕСРЕДНЕЙ
ОСАДКИ
ПРИ
ПРИЕМЕ
ИЛИ
РАСХОДОВАНИИ ГРУЗОВ
Если в произвольном месте на судне принимают или расходуют груз,
то возникает не только изменение средней осадки, но также крен и
дифферент.
Чтобы не было ни крена ни дифферента, необходимо ЦТ груза
расположить на вертикали, проходящей через ЦВ добавочного слоя
водоизмещения; в этом случае изменится только средняя осадка.
Практически целесообразно различать два случая:
а) П р и е м и л и р а с х о д о в а н и е м а л о г о г р у з а . Если груз по весу
мал, т.е. не превосходит примерно 10% от водоизмещения, то изменение
средней осадки определяется выражением
p
м,
(79)
T
S
где вес груза p берется со знаком плюс в случае его приема на судно и со
знаком минус в случае его расходования.
Число тонн на сантиметр осадки
q 0,01 S кН/см.
(80)
В таком случае изменение средней осадки будет:
p
см.
(81)
T
q
25.
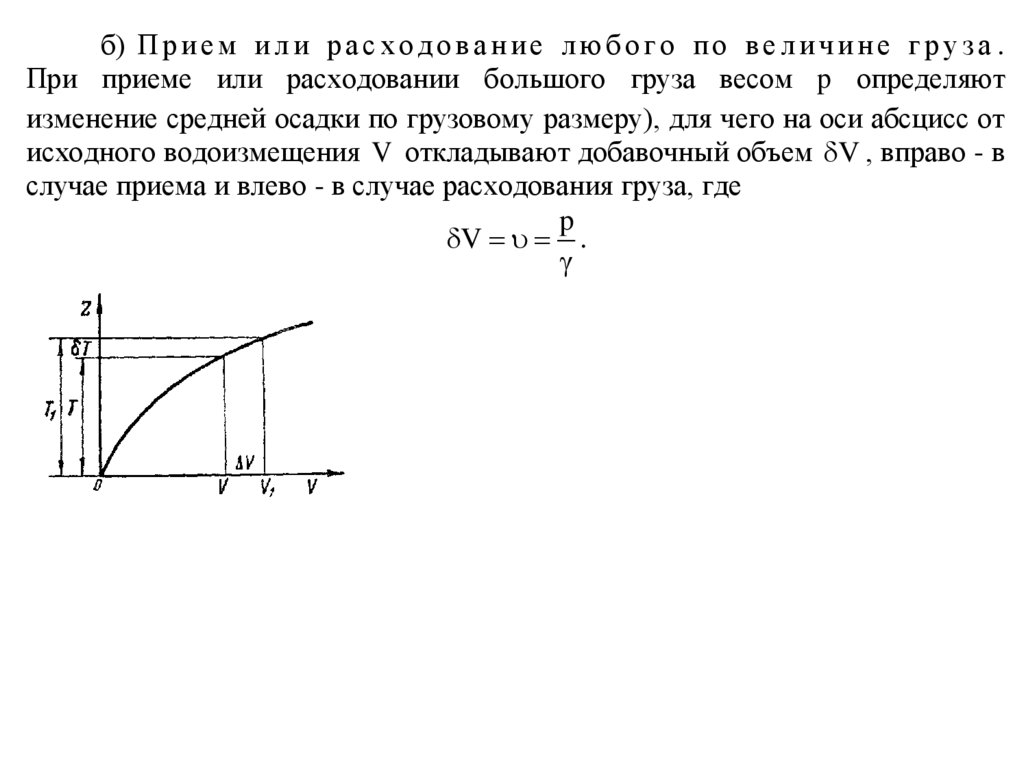
б) П р и е м и л и р а с х о д о в а н и е л ю б о г о п о в е л и ч и н е г р у з а .При приеме или расходовании большого груза весом p определяют
изменение средней осадки по грузовому размеру), для чего на оси абсцисс от
исходного водоизмещения V откладывают добавочный объем V , вправо - в
случае приема и влево - в случае расходования груза, где
p
V .
26.
Таким образом, окончательное водоизмещениеV1 V V .
(82)
Чтобы не было ни крена ни дифферента, необходимо поместить ЦТ
груза на вертикали, проходящей через ЦВ добавочного слоя водоизмещения,
координаты которого определяются следующим выражением:
V1x c1 Vx c
x
(83)
V
y 0
где x c и x c1 - абсциссы ЦВ соответствующих водоизмещении V и V1 ,
которые снимаются с кривой x c f z
27.
ИЗМЕНЕНИЕ СРЕДНЕЙ ОСАДКИ ПРИ ИЗМЕНЕНИИ СОЛЕНОСТИВОДЫ
Если судно переходит из воды с объемным весом 1 при осадке T1 в
воду с объемным весом 2 то осадки примерно обратно пропорциональны
объемным весам, т.е.
T1 2
,
(84)
T2 1
а изменение осадки
V
T 1 2
2
S
или
T 1 2 1T1 ,
(85)
2
где 1 - коэффициент вертикальной полноты, соответствующий исходному
водоизмещению V1 .
Вместе с изменением осадки судно обычно несколько изменяет свой
дифферент; этого не будет, если ЦТ площади действующей ватерлинии
лежит на одной вертикали с ЦВ судна.
28.
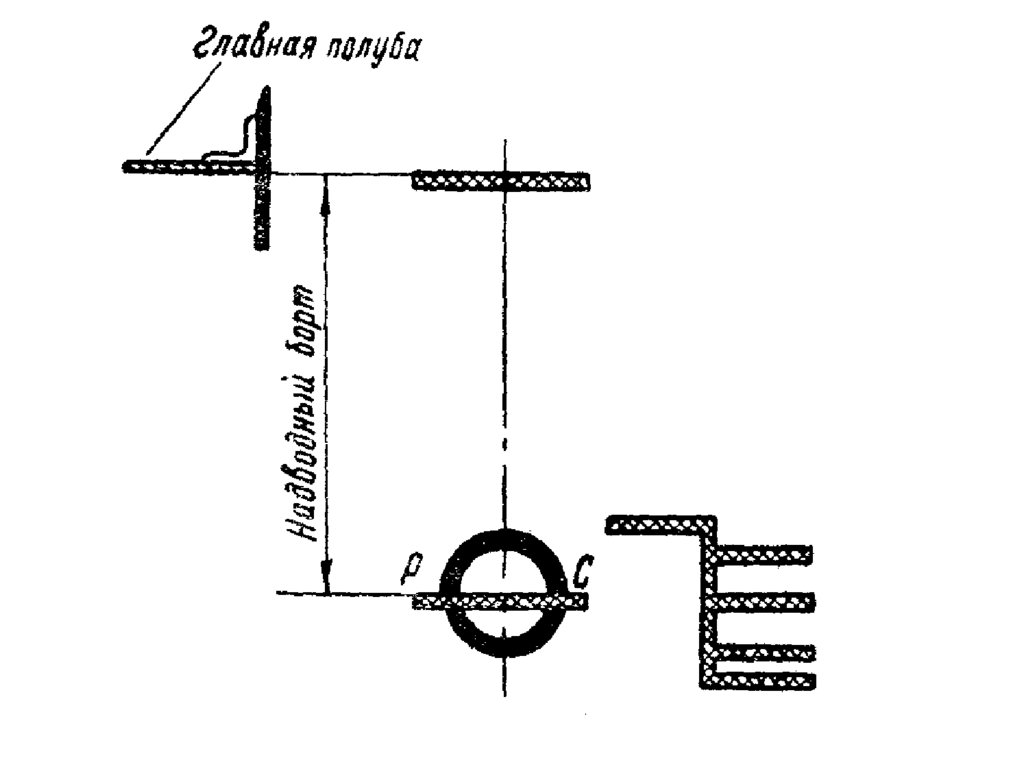
ЗАПАС ПЛАВУЧЕ СТИЗапас плавучести судна определяется водонепроницаемым объемом надводной части
корпуса судна, включая в этот объем, кроме
основного корпуса, также водонепроницаемые надстройки. Если же в борту имеются
вырезы, которые не могут быть закрыты водонепроницаемо, то запас плавучести определяется объемом корпуса до нижней кромки
этих отверстий.
29.
30.
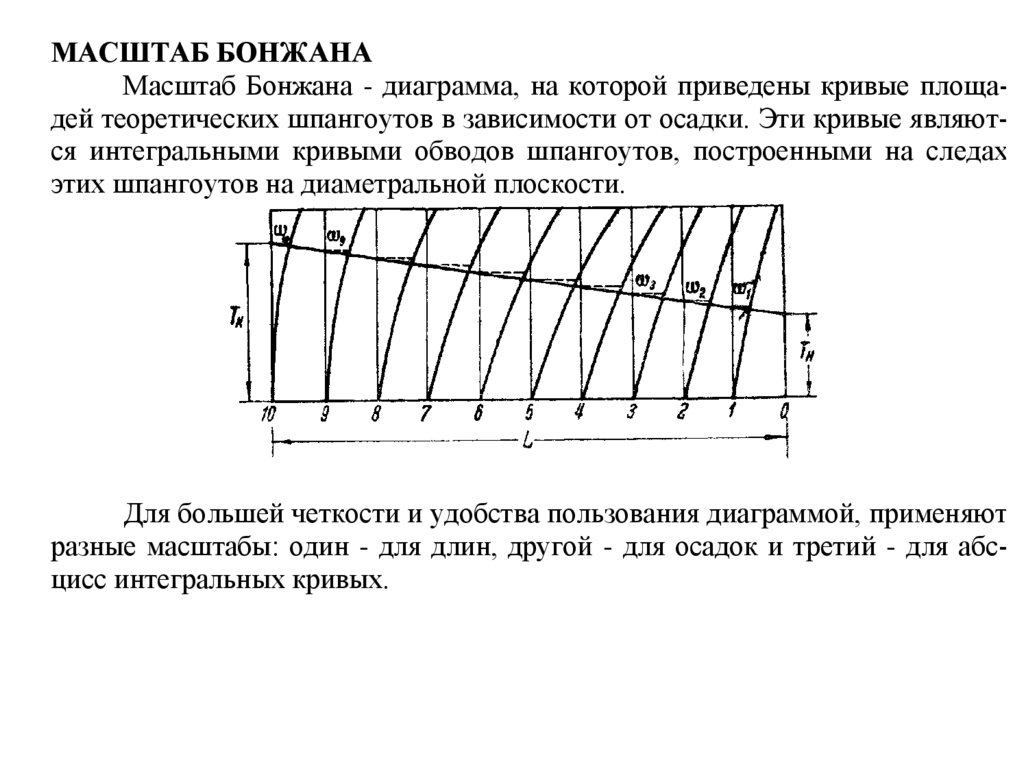
МАСШТАБ БОНЖАНАМасштаб Бонжана - диаграмма, на которой приведены кривые площадей теоретических шпангоутов в зависимости от осадки. Эти кривые являются интегральными кривыми обводов шпангоутов, построенными на следах
этих шпангоутов на диаметральной плоскости.
Для большей четкости и удобства пользования диаграммой, применяют
разные масштабы: один - для длин, другой - для осадок и третий - для абсцисс интегральных кривых.
31.
Масштабом Бонжана пользуются для вычислений объемного водоизмещения и абсциссы ЦВ при посадке судна с любым дифферентом, но безкрена. Для этого на следах концевых шпангоутов наносят осадки носом Tн и
кормой Tк в соответствующих масштабах и проводят прямую WL , являющуюся следом действующей ватерлинии. В точках пересечения следа ватерлинии со следом шпангоутов проводят абсциссы интегральных кривых, которые выражают, в масштабе, площади i , погруженных частей шпангоутов.
Для расчета искомых величин пользуемся формулами
L
2
V dx ;
L
2
L
2
x dx
xc
L
2
L
2
dx
L
2
.
32.
Вычисление выполняется по приближенным формулам квадратур поправилу трапеций или по правилу Чебышева, в зависимости от того, как размещены шпангоуты на диаграмме.
Соответствующие расчетные формулы:
а) По правилу трапеций
m
m
V L i i u ;
i 0
x c L
i a
i 0
m
i
u
i 0
б) По правилу Чебышева
n
L n
V i ;
n i 1
i
k i i
L
x c i 1n
.
2
i
i 1
i
i
1
.


























 mechanics
mechanics








