Similar presentations:
Понятие алгебры логики. Законы алгебры логики. Построение таблиц истинности
1.
Понятие алгебры логики. Законыалгебры логики. Построение таблиц
истинности
Лекция 9.11
2.
Алгебра логикиАлгебра логики — раздел математики,
изучающий высказывания,
рассматриваемые с точки зрения их
логических значений (истинности или
ложности), и логические операции над
ними.
3.
Логическоевысказывание
Логическое высказывание — это
повествовательное предложение, в отношении
которого можно однозначно сказать, истинно оно
или ложно.
Примеры:
1. "2 + 2 = 5." - Это высказывание является ложным,
так как математически верное равенство 2 + 2
равно 4, а не 5.
2. "Вода кипит при температуре 100 градусов
Цельсия." - Это высказывание является истинным,
так как вода действительно кипит при температуре
100 градусов Цельсия при нормальных условиях.
4.
Логическаяпеременная
Логическая переменная — это переменная, которая
обозначает любое высказывание и может
принимать логические значения «истина» или
«ложь». Для логических значений «истина» —
«ложь» могут использоваться следующие
обозначения: Истина — Ложь, True — False, да —
нет, 1 — 0.
Логическая операция полностью может быть
описана таблицей истинности, указывающей, какие
значения принимает составное высказывание при
всех возможных значениях образующих его
элементарных высказываний.
5.
И их таблицы истинностиЛогические
операции
6.
Высказыванию ставится в соответствие новоевысказывание, значение которого
противоположно исходному.
Отрицание (инверсия, логическое
НЕ)
7.
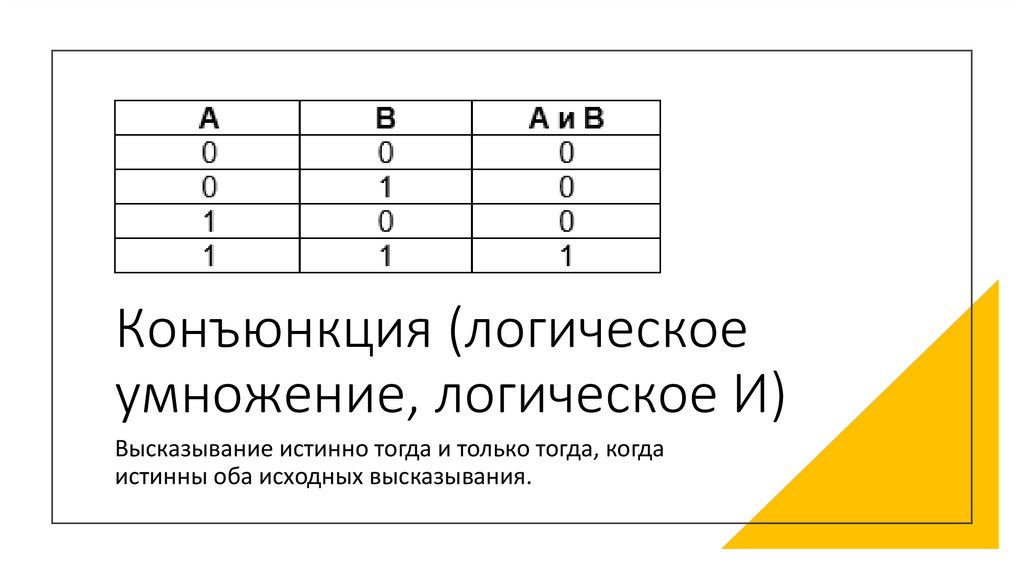
Конъюнкция (логическоеумножение, логическое И)
Высказывание истинно тогда и только тогда, когда
истинны оба исходных высказывания.
8.
Дизъюнкция (логическоесложение, логическое ИЛИ)
Высказывание ложно тогда и только тогда, когда
ложны оба исходных высказывания.
9.
Импликация (логическое следование)Логическая операция, ставящая в соответствие двум высказываниям
новое, являющееся ложным тогда и только тогда, когда первое
высказывание (посылка) истинно, а второе (следствие) — ложно.
10.
Строгая (исключающая) дизъюнкцияЛогическая операция, ставящая в соответствие двум высказываниям
новое, являющееся истинным тогда и только тогда, когда только
одно из двух высказываний истинно.
Пример: «Либо пан, либо пропал».
11.
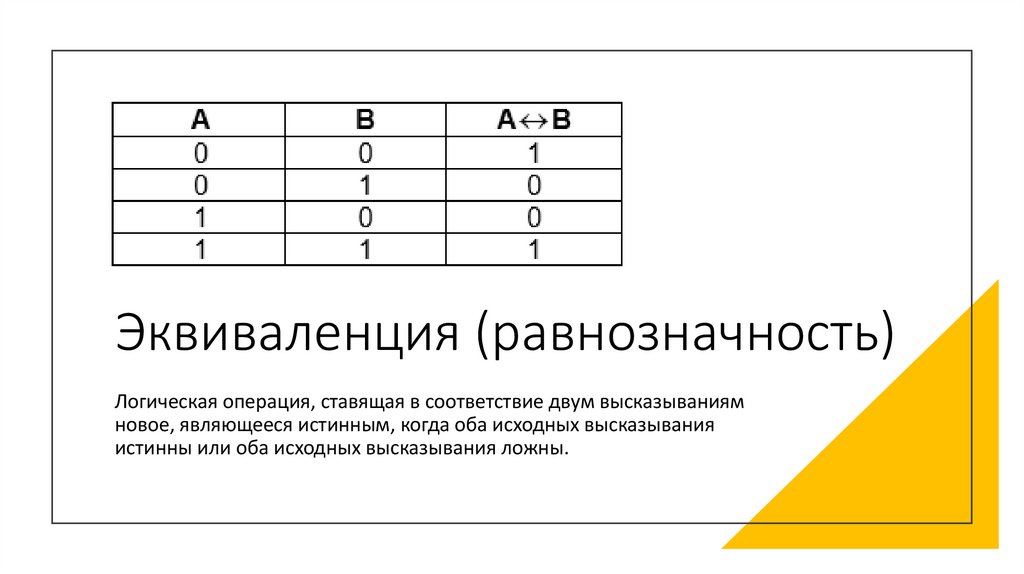
Эквиваленция (равнозначность)Логическая операция, ставящая в соответствие двум высказываниям
новое, являющееся истинным, когда оба исходных высказывания
истинны или оба исходных высказывания ложны.
12.
Порядок операций1. Скобки
2. Отрицание
3. Конъюнкция
4. Дизъюнкция
5. Импликация
6. Эквиваленция
13.
Решим задачку. Шаг 1Запишем в форме логического выражения составное(сложное)
высказывание «(2*2=5 или 2*2=4) и НЕ 2*2=5 или НЕ 2*2=4».
Проанализируем составное высказывание. Оно состоит из двух
простых высказываний:
А = «2х2=5» - ложно (0),
В = «2х2=4» - истинно (1).
Тогда составное высказывание можно записать в следующей
форме:
14.
Решим задачку. Шаг 2Теперь необходимо записать высказывание в форме логического
выражения с учетом последовательности выполнения логических
операций. При выполнении логических операций определен
следующий порядок их выполнения: инверсия, конъюнкция,
дизъюнкция. Для изменения указанного порядка могут
использоваться скобки.
15.
Решим задачку. Шаг 3Истинность или ложность составных высказываний можно
определять чисто формально, руководствуясь законами алгебры
высказываний, не обращаясь к смысловому содержанию
высказываний.
Подставим в логическое выражение значения логических
переменных и, используя таблицы истинности базовых
логических операций, получим значение логической функции:
16.
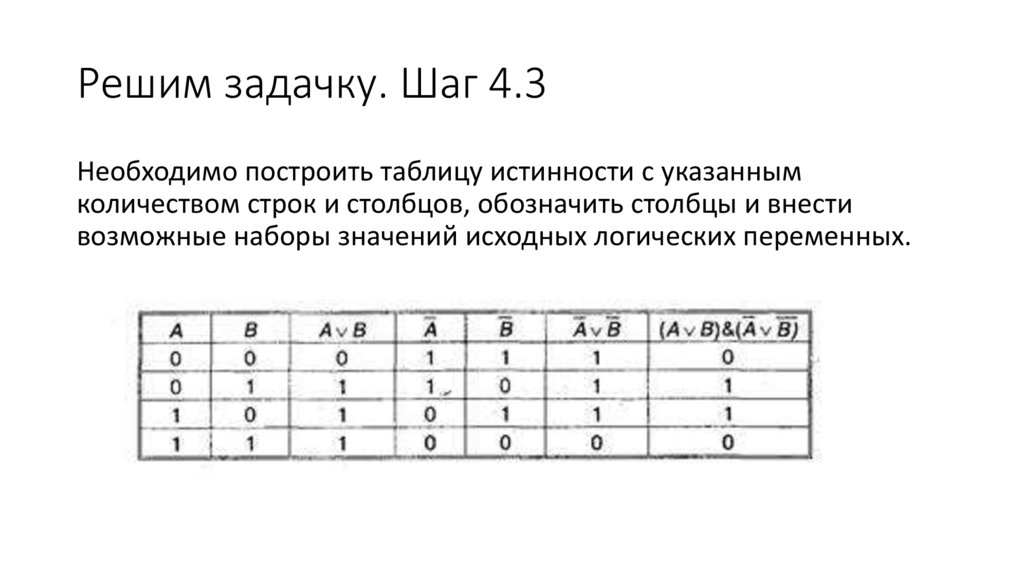
Построим таблицу истинности17.
Решим задачку. Шаг 4.1Для каждого составного высказывания можно построить таблицу
истинности, которая определяет его истинность или ложность при всех
возможных комбинациях исходных значений простых высказываний
(логических переменных).
При построении таблиц истинности целесообразно руководствоваться
определенной последовательностью действий:
Необходимо определить количество строк в таблице истинности, которое
равно количеству возможных комбинаций значений логических
переменных, входящих в логическое выражение. Если количество
логических переменных n, то:
Кол-во строк = 2

























 informatics
informatics








