Циклы на языке Паскаль. Постановка задачи

1. Циклы на языке Паскаль

2.

3. 1 этап. Постановка задачи

Задание. Дано N кубиков, на которых написаны
разные буквы.
Сколько различных N-буквенных слов можно
составить из этих кубиков (слова не
обязательно должны иметь смысл)?
Обозначим искомую целочисленную
величину буквой F.
Тогда постановка задачи выглядит
следующим образом:
Дано: N
Найти: F

4. 2 этап. Математическая формализация

Разберём примеры:
1. Имеются два кубика с буквами «И» и «К».
Из них можно составить два слова (2): ИК и КИ
2. Добавим третью букву, «С».
Теперь число разных слов будет в три раза
больше предыдущего, т.е. 6:
ИКС, КИС, ИСК, КСИ, СКИ, СИК
3. Если добавить четвёртую букву, например
«А», то число слов возрастёт в четыре раза и
станет равна 24.
и т.д.

5. 2 этап. Математическая формализация

Подобные задачи решает раздел математики,
который называется комбинаторикой.
Количество разных комбинаций из N предметов,
получаемых изменением их порядка, называется
числом перестановок.
Это число выражается функцией от N: N!
1! = 1
2! = 1·2 = 2
3! = 1·2·3 = 6
4! = 1·2·3·4 = 24
5! = 1·2·3·4·5 = 120
и т.д.

6. 2 этап. Математическая формализация

Значит, возвращаясь к задаче, если
N обозначает количество букв,
а F – количество слов из этих букв,
то расчётная формула такова:
F = N! = 1·2·…·N

7. 3 этап. Построение алгоритма

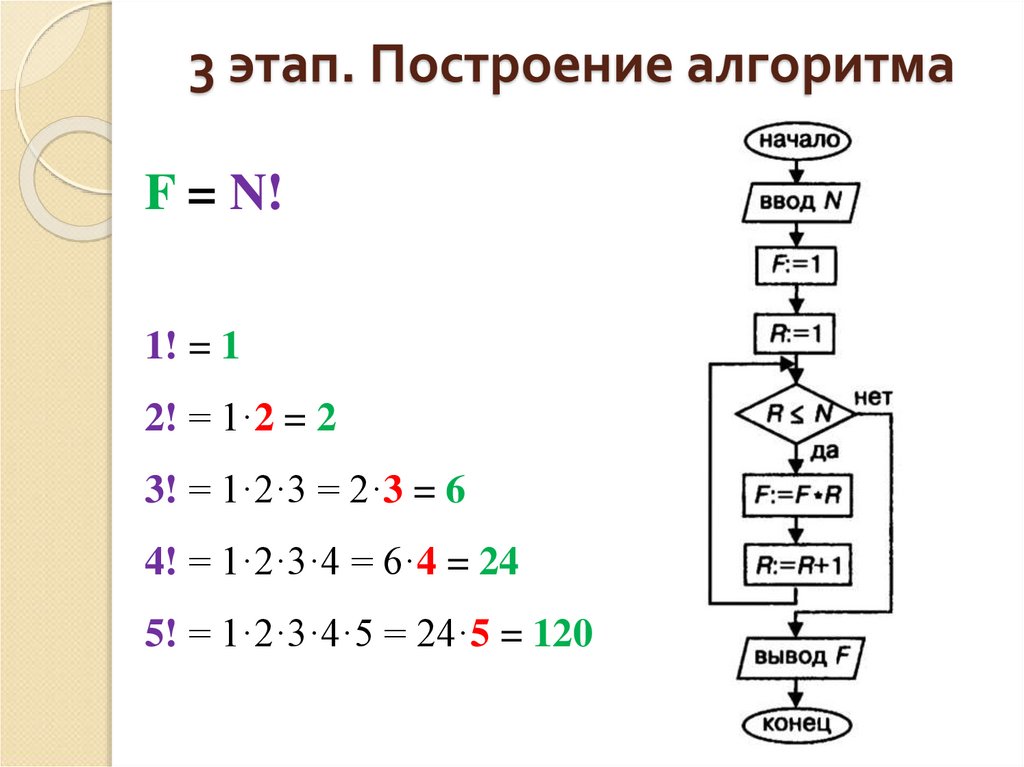
8. 3 этап. Построение алгоритма

F = N!
1! = 1
2! = 1·2 = 2
3! = 1·2·3 = 2·3 = 6
4! = 1·2·3·4 = 6·4 = 24
5! = 1·2·3·4·5 = 24·5 = 120

9. 4 этап. Составление программы

Основной циклической структурой является цикл с предусловием:
while <выражение> do <оператор>

10. 5 этап. Отладка и тестирование

Под отладкой программы понимается процесс
испытания работы программы и исправления
обнаруженных ошибок.
Под тестированием программы понимается
поиск алгоритмических ошибок в программе.
Тест – это конкретный вариант значений
исходных данных, для которого известен
ожидаемый результат.
Тестирование нашей программы:
Введите число букв: 6
Из 6 букв можно составить 720 слов

11. 6 этап. Проведение расчётов и анализ полученных результатов

Этот этап технологической цепочки
реализуется при разработке
практически полезных (не учебных)
программ.
В процессе эксплуатации такие
программы могут дорабатываться и
совершенствоваться.

12. Алгоритм Евклида

Наибольший общий делитель (НОД)
двух натуральных чисел – это самое
большое натуральное число, на
которое они оба делятся нацело.
Например, у чисел 12 и 18 общие
делители следующие: 2, 3, 6.
Наибольшим общим делителем
является число 6.
НОД (12, 18) = 6

13. Алгоритм Евклида

Задание. Требуется составить
программу определения наибольшего
общего делителя (НОД) для двух
натуральных чисел.
Обозначим исходные данные как M и N:
Дано: M, N
Найти: НОД (M, N)
Это задание будем решать с помощью
алгоритма Евклида.

14. Алгоритм Евклида

Идея алгоритма Евклида сводится к
двум свойствам:
1. Если M > N, то
НОД (M, N) = НОД (M – N, N)
НОД двух натуральных чисел
равен НОД их положительной
разности (модуля их разности) и
меньшего числа.
2. НОД (M, M) = M

15. Алгоритм Евклида

Для «ручного» счёта алгоритм
Евклида выглядит так:
1. Если числа равны, то взять любое из
них в качестве ответа, в противном
случае продолжить выполнение
алгоритма
2. Заменить большее число разностью
большего и меньшего из чисел
3. Вернутся в выполнению п.1

16. Алгоритм Евклида

На пример, M = 32, N = 24
M
N
32
24
8
24
8
16
8
8
Получили: НОД (32, 24) = НОД (8, 8) = 8

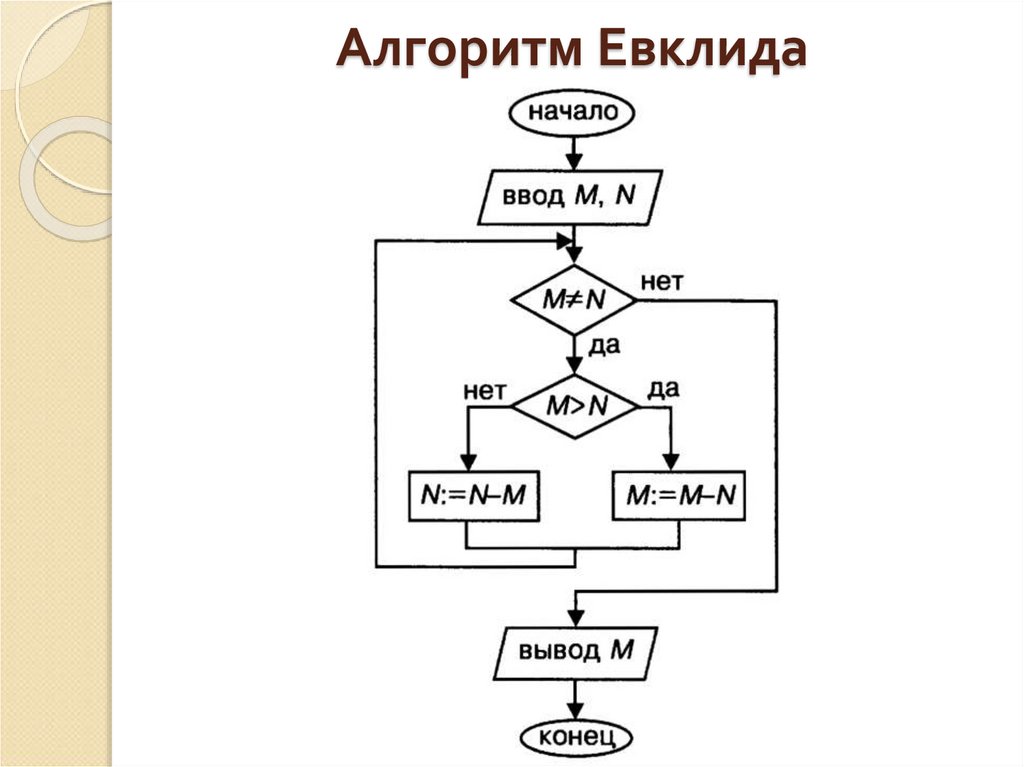
17. Алгоритм Евклида

18. Алгоритм Евклида

19.

Домашнее задание
Изучить § 15, 16
Изучить конспект