Similar presentations:
Фрактальная структура треугольника Паскаля как основа многоуровневой системы счисления
1.
Государственное бюджетное нетиповое общеобразовательное учреждениеСамарской области “Самарский региональный центр для одаренных детей”
Фрактальная структура треугольника Паскаля
как основа многоуровневой системы счисления
Выполнила:
Караулова Юлия Сергеевна,
ученица 9 «А» класса
ГБНОУ СО «СРЦОД»
Научный руководитель:
учитель математики ГБНОУ СО
«СРЦОД»
Горячева Ольга Васильевна
2.
Актуальность работы: треугольник Паскаля является стратегическим объектомматематики,
являющимся
основой
фрактальной
геометрии.
Особенности
свойств
треугольника Паскаля позволяют описать многообразие геометрических форм неживой и
живой природы.
Цель работы - исследовать оригинальные свойства треугольника Паскаля, провести их
анализ и использовать для решения ряда задач.
Задачи исследовательской работы:
- выявить свойства чисел, входящих в структуру треугольника Паскаля;
- исследовать различные комбинации диагоналей треугольника Паскаля;
- установить аналогию строения числового треугольника Паскаля с треугольником
Серпинского, одним из основных фигур фрактальной геометрии;
- рассмотреть основы строения чисел Фибоначчи;
- решить ряд аналитических и логических задач.
3.
Структура треугольника ПаскаляТреугольник Паскаля - форма записи упорядоченных биномиальных
коэффициентов в виде бесконечного треугольного массива, имеющего свое
начало в комбинаторике и теории вероятностей.
4.
Свойства треугольника ПаскаляСвойство 1
Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать
неограниченно.
Свойство 2
Первая диагональ – простая диагональ, состоящая из единиц.
Свойство 3
Вторая диагональ - натуральные числа, расположенные в порядке возрастания
1, 2, 3, 4, 5 и т.д.
5.
Свойство 4Числа третьей диагонали называются треугольными, так как из количества точек, равном любому из
чисел, можно построить равносторонний треугольник.
Свойство 5
Четвертая диагональ треугольника Паскаля - это «пирамидальные» числа или, тетраэдральные числа,
показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).
Свойство 6
Сумма чисел, стоящих на четных места, равна сумме чисел, стоящих на нечетных местах и каждая из них
составляет 2n-1 .
6.
Свойство 7Сумма чисел, стоящих в любой строке треугольника, вдвое больше суммы чисел, стоящей в предыдущей
строке.
Свойство 8
Суммы чисел, стоящих в строках треугольника Паскаля,
образуют геометрическую прогрессию с первым членом,
равным 1, и знаменателем 2: 1, 2, 4, 8, ... .
Свойство 9
Каждое число в таблице, будучи уменьшенным на единицу,
равно сумме всех чисел, заполняющих пространство,
ограниченное теми диагоналями,
на пересечении которых стоит это число.
7.
Свойство 10Каждое число треугольника равно сумме чисел, расположенных в диагонали,
находящейся над этим числом.
Свойство 11
Если номер строки треугольника Паскаля – простое число, то все числа этой строки,
кроме 1, делятся на это число.
Свойство 12
Числа, стоящие на горизонтальных строках треугольника Паскаля,
- это биномиальные коэффициенты, то есть коэффициенты разложения
(a+b)^n по степеням.
8.
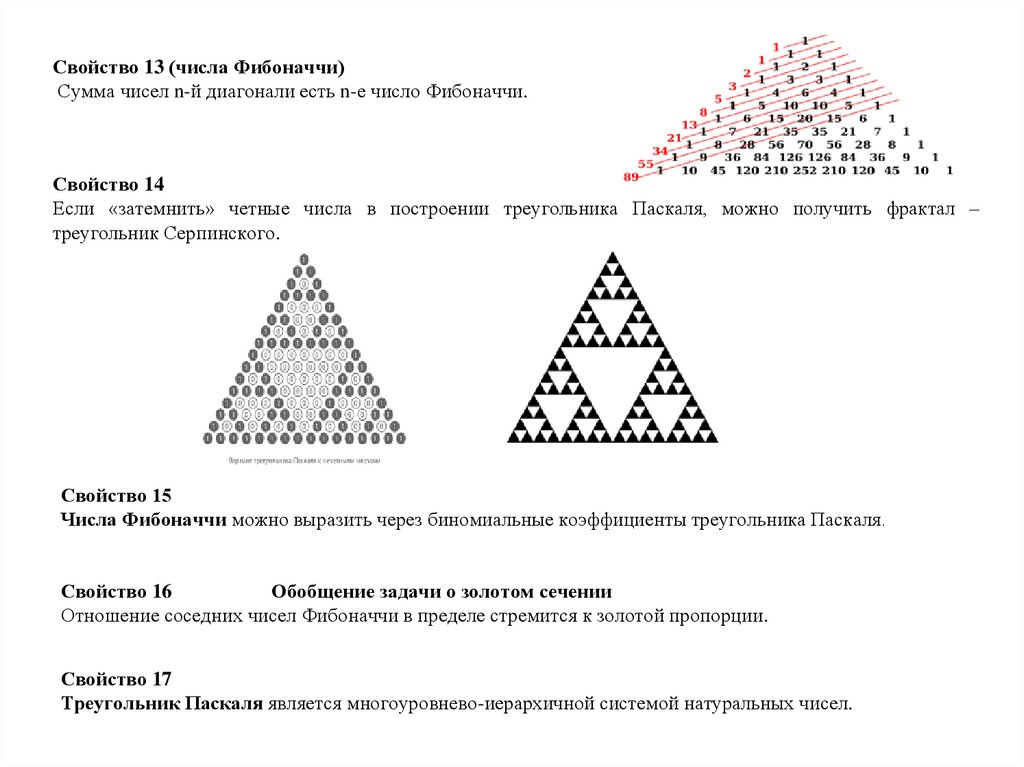
Свойство 13 (числа Фибоначчи)Сумма чисел n-й диагонали есть n-е число Фибоначчи.
Свойство 14
Если «затемнить» четные числа в построении треугольника Паскаля, можно получить фрактал –
треугольник Серпинского.
Свойство 15
Числа Фибоначчи можно выразить через биномиальные коэффициенты треугольника Паскаля.
Свойство 16
Обобщение задачи о золотом сечении
Отношение соседних чисел Фибоначчи в пределе стремится к золотой пропорции.
Свойство 17
Треугольник Паскаля является многоуровнево-иерархичной системой натуральных чисел.
9.
ФракталыФрактал (лат. fractus — дробленый, сломанный, разбитый) — множество, обладающее свойством
самоподобия.
«Фрактал» не является математическим термином. Обычно так называют геометрическую фигуру, которая
удовлетворяет одному или нескольким из следующих свойств:
обладает сложной структурой при любом увеличении;
является (приближённо) самоподобной;
обладает дробной фрактальной размерностью, которая больше топологической;
может быть построена рекурсивными процедурами.
Кривая Коха
Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в
одной точке.
Снежинка Коха
Треугольник Серпинского
Чтобы получить этот фрактал, нужно взять равносторонний треугольник с внутренностью, провести в нём
средние линии и убрать центральный из четырех образовавшихся маленьких треугольников. Дальше эти же
действия нужно повторить с каждым из оставшихся трех треугольников, и т. д.
10.
Свойства последовательности Фибоначчи11.
Решение задач с помощью треугольника ПаскаляЗадача 1
В магазин доставили 6 компьютеров, их необходимо расставить по 3 в ряд. Сколькими
способами можно это сделать?
12.
Задача 2Сколькими способами можно расставить 9 цветов по 3 штуки в букет?
13.
Задача 3Вычислить степень числа 118.
Для вычисления степени числа 11 используем треугольник Паскаля. Цифры, расположенные в
третьей, четвертой и пятой строках, образуют число, представляющее собой вторую, третью и
четвертую степени числа 11. Значит, для нахождения искомой степени следует нарисовать
треугольник Паскаля с соответствующим количеством строк. Но после пятой и выше степеней
наблюдается несоответствие. Рассмотрим соответствующую строчку для нахождения пятой степени
числа 11. Если число треугольника Паскаля получается двузначным, то справа налево в старший
разряд перебрасываем количество десятков и складываем с числом, стоящим слева. Полученная
последовательность и есть результат.
18285670562881
2 1 4 3 5 8 8 8 1 = 118
14.
Задача 4В студенческий городок ведет один вход. Далее каждый перекресток разделяет одну дорогу на две.
В город входит 28 человек. Далее на каждом последующем перекрестке их количество делится
пополам. Какое количество студентов в результате будет на каждом перекрестке, если далее они уже
не смогут разделяться?
Пример для 25
Для n = 8 это 8 строка треугольника Паскаля.
1
8 28 56 70 56 28 8 1
15.
Задача о сумме чисел ФибоначчиНайти сумму первых n чисел Фибоначчи с номерами, кратными 2.
Решение. Нам нужно найти сумму: u2 + u4 + u6 + … + u2n.
По формуле Бине:
В
скобках сумма геометрической прогрессии
Можно проверить с помощью треугольника Паскаля для суммы четных членов
последовательности Фибоначчи. Например, сумма первых четырех четных номеров равна
16.
Цель работы достигнута. Детальное исследование показывает, чтодиагональные суммы треугольника Паскаля образуют двоичный код, что
является основой двоичной системы счисления; другие диагональные
суммы, являющиеся основой иррациональных систем, представляют
последовательность Фибоначчи. Свойство представления треугольника в
виде фрактала может порождать новые более эффективные
информационные системы.
Применение свойств треугольника Паскаля безгранично и достойно
дальнейшего более детального исследования.















 programming
programming








