Деревья и графы

1.

Деревья и графы
Группа: ККСО-07-22
Плашкин Сергей
Аринин Артем

2.

Графовые структуры играют важную роль в
современном мире, особенно в
информационных технологиях. Они
используются для моделирования и анализа
различных систем и сетей, таких как
социальные сети, транспортные сети,
маршруты данных в компьютерных сетях,
связи между белками и генами в
биоинформатике, а также для анализа
больших объемов данных.
Графовые структуры позволяют представлять
сложные взаимосвязи между объектами и
процессами, что делает их эффективным
инструментом для анализа и визуализации
данных. Они также широко применяются в
разработке алгоритмов машинного обучения,
оптимизации и принятия решений.

3.

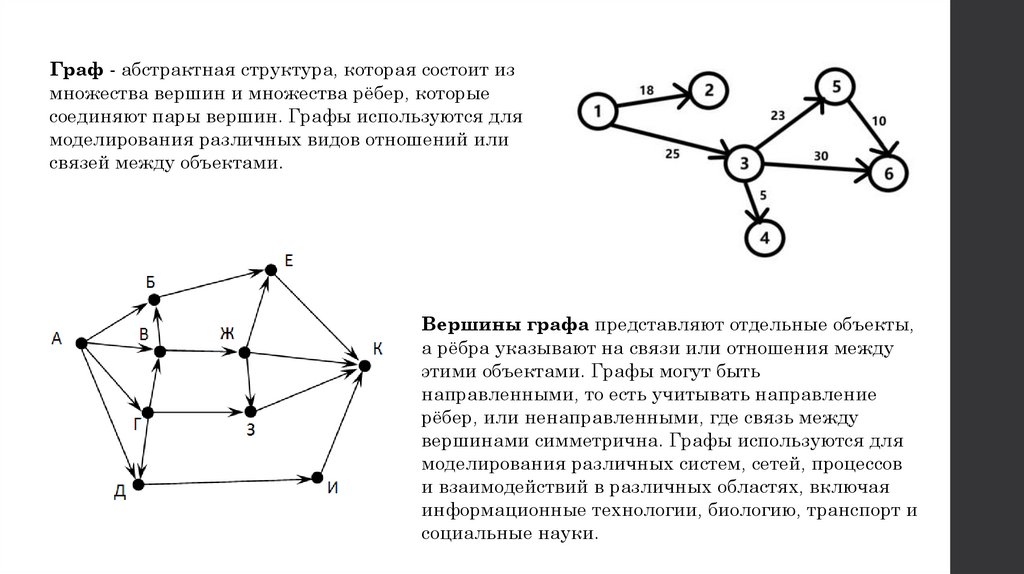
Граф - абстрактная структура, которая состоит из
множества вершин и множества рёбер, которые
соединяют пары вершин. Графы используются для
моделирования различных видов отношений или
связей между объектами.
Вершины графа представляют отдельные объекты,
а рёбра указывают на связи или отношения между
этими объектами. Графы могут быть
направленными, то есть учитывать направление
рёбер, или ненаправленными, где связь между
вершинами симметрична. Графы используются для
моделирования различных систем, сетей, процессов
и взаимодействий в различных областях, включая
информационные технологии, биологию, транспорт и
социальные науки.

4.

Теория графов - это раздел дискретной
математики, который изучает свойства и применение
графов. Анализ графов с использованием различных
алгоритмов и методов имеет широкое применение в
программировании, анализе данных, сетевой теории
и других областях.

5.

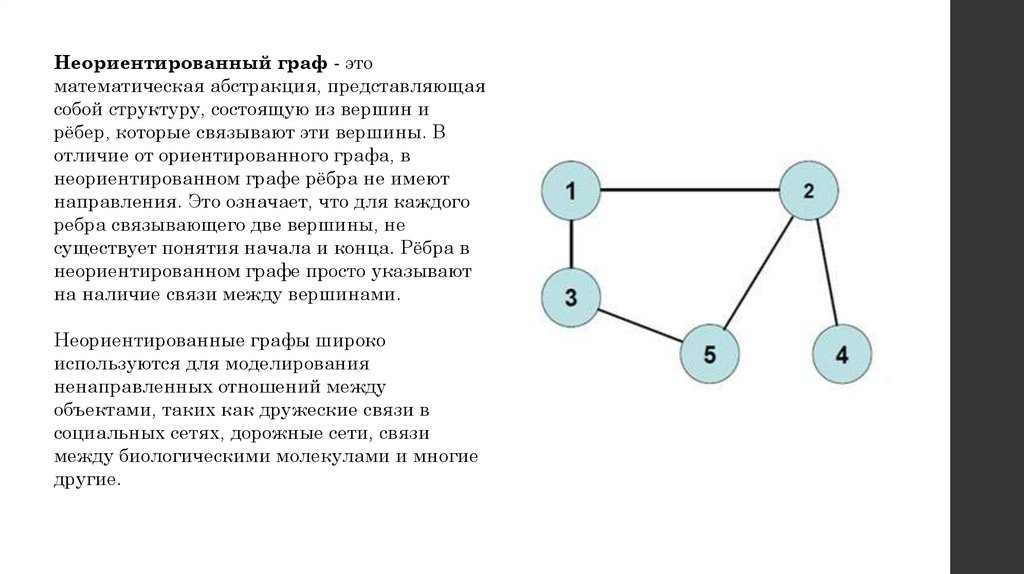
Неориентированный граф - это
математическая абстракция, представляющая
собой структуру, состоящую из вершин и
рёбер, которые связывают эти вершины. В
отличие от ориентированного графа, в
неориентированном графе рёбра не имеют
направления. Это означает, что для каждого
ребра связывающего две вершины, не
существует понятия начала и конца. Рёбра в
неориентированном графе просто указывают
на наличие связи между вершинами.
Неориентированные графы широко
используются для моделирования
ненаправленных отношений между
объектами, таких как дружеские связи в
социальных сетях, дорожные сети, связи
между биологическими молекулами и многие
другие.

6.

В ориентированный графе, в отличие от
неориентированного графа, каждое ребро имеет
определенное направление, указывающее на
отношение между вершинами от источника к
конечной точке.
Ориентированные графы часто используются для
моделирования направленных отношений или
связей между объектами, например, поток
информации, транспортные маршруты, зависимости
времени и многие другие. Такие графы широко
применяются в различных областях, включая
информационные технологии, транспортные
системы, биоинформатику и другие.

7.

Интерпретация графов относится к процессу понимания и извлечения информации из
графовых структур. Существует множество методов интерпретации графов, в том числе:
1. Анализ структуры графа: Этот метод включает в себя изучение характеристик графа,
таких как его диаметр, радиус, степени вершин, плотность и др. Анализ структуры графа
помогает понять основные свойства и форму графа.
2. Алгоритмы поиска путей: Эти методы используются для нахождения кратчайших путей,
циклов или других путей в графе. Например, алгоритмы Дейкстры и алгоритмы поиска в
глубину/ширину.
3. Визуализация графов: Визуализация помогает интерпретировать графическую структуру
графа и понять его особенности и характеристики.
4. Кластеризация: Метод кластеризации графов используется для обнаружения плотно
связанных подграфов в графе, что может помочь в выявлении структурных особенностей и
группировке вершин.
5. Анализ центральности: Этот метод позволяет выявлять наиболее важные вершины в
графе, основываясь на различных характеристиках, таких как центральность по посредничеству
или степени.

8.

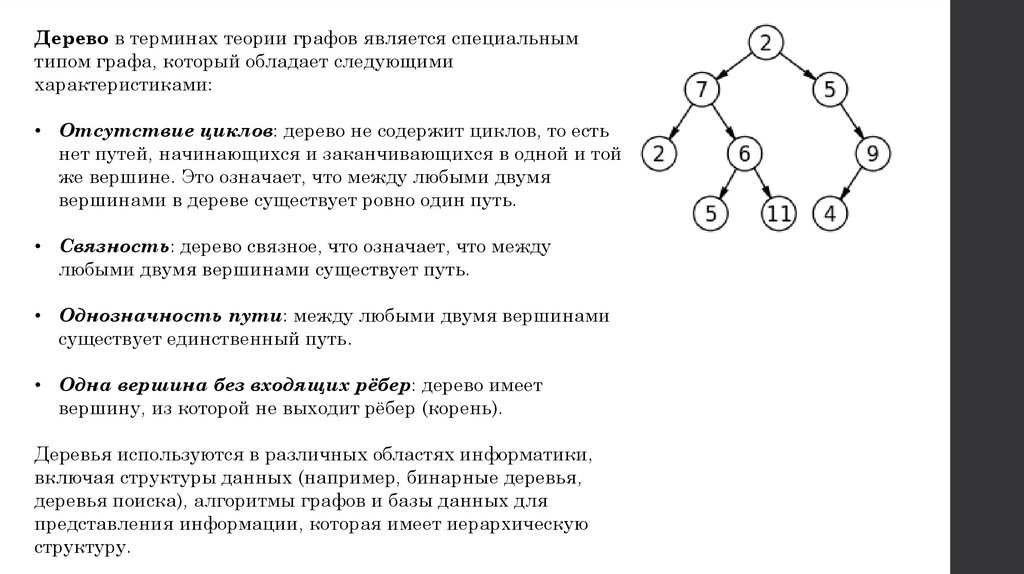
Дерево в терминах теории графов является специальным
типом графа, который обладает следующими
характеристиками:
• Отсутствие циклов: дерево не содержит циклов, то есть
нет путей, начинающихся и заканчивающихся в одной и той
же вершине. Это означает, что между любыми двумя
вершинами в дереве существует ровно один путь.
• Связность: дерево связное, что означает, что между
любыми двумя вершинами существует путь.
• Однозначность пути: между любыми двумя вершинами
существует единственный путь.
• Одна вершина без входящих рёбер: дерево имеет
вершину, из которой не выходит рёбер (корень).
Деревья используются в различных областях информатики,
включая структуры данных (например, бинарные деревья,
деревья поиска), алгоритмы графов и базы данных для
представления информации, которая имеет иерархическую
структуру.

9.

Части дерева:
• Корень: самый верхний узел дерева, также
называемый корневым узлом.
• Узел: объект с ключом или значением и
указателями на дочерние узлы. Узлы без
дочерних узлов называют листьями или
терминальными узлами.
• Внутренний узел: узел, у которого есть хотя бы
один дочерний узел.
• Ветвь: связывает два узла.

10.

Бинарное дерево - это иерархическая структура
данных, состоящая из узлов, где каждый узел имеет
не более двух потомков. Один из потомков
называется левым, а другой - правым. Бинарное
дерево может быть пустым (не содержащим ни
одного узла), или состоять из корня и нуля, одного
или двух поддеревьев, каждое из которых также
является бинарным деревом.
Бинарные деревья могут быть сбалансированными
или несбалансированными, что влияет на их
эффективность при выполнении различных
операций. Сбалансированные бинарные деревья
имеют более предсказуемую производительность,
поскольку глубина поддеревьев отличается не более
чем на один уровень, в то время как
несбалансированные могут иметь большие различия
в глубине, что влияет на скорость выполнения
операций.

11.

Прямой обход бинарного дерева обозначает
обход узлов в следующем порядке: первый
посещается корень, затем левое поддерево, и,
наконец, правое поддерево. Обратный
порядок обхода (post-order traversal)
предполагает обход левого поддерева, затем
правого поддерева, и в конце посещение корня.
Таким образом, чтобы вычислить левые
листовые узлы в обратном порядке обхода, наш
алгоритм будет выглядеть следующим образом:
1. Рекурсивно выполним обход левого
поддерева.
2. Рекурсивно выполним обход правого
поддерева.
3. Если текущий узел - левый лист, то добавим
его значение в результирующий список.

12.

Для построение эйлерового пути в
неориентированном графе можно
использовать следующий алгоритм:
1. Проверить связность графа.
2. Найти вершину с нечетной степенью
(или выбрать любую, если все вершины
имеют четные степени).
3. Начать обход графа, удаляя пройденные
рёбра.
4. Продолжать обход, пока не вернетесь в
начальную вершину или пока не будете
вынуждены остановиться.
5. Когда обход будет завершен, получить
эйлеров путь в графе.

13.

СПАСИБО ЗА
ВНИМАНИЕ