Similar presentations:
Дерево всех вариантов. Информатика
1.
Дерево всехвариантов
2.
МКДеревья
Иерархия - это расположение частей или элементов целого в
порядке от высшего к низшему. Системы, элементы которых находятся в
отношениях «является разновидностью», «входит в состав» и других
отношениях подчиненности, называются иерархическими системами.
Граф иерархической системы называется деревом.
Отличительной особенностью дерева является то, что между любыми
двумя его вершинами существует единственный путь. Дерево не
содержит циклов и петель.
Обычно у дерева выделяется одна главная вершина, которая
называется корнем дерева. Каждая вершина дерева (кроме корня) имеет
только одного предка — обозначенный ею объект входит в один класс
верхнего уровня. Любая вершина дерева может порождать несколько
потомков — вершин, соответствующих классам нижнего уровня. Такой
принцип связи называется «один ко многим». Вершины, не имеющие
порожденных вершин, называются листьями.
3.
МКДрево всех вариантов
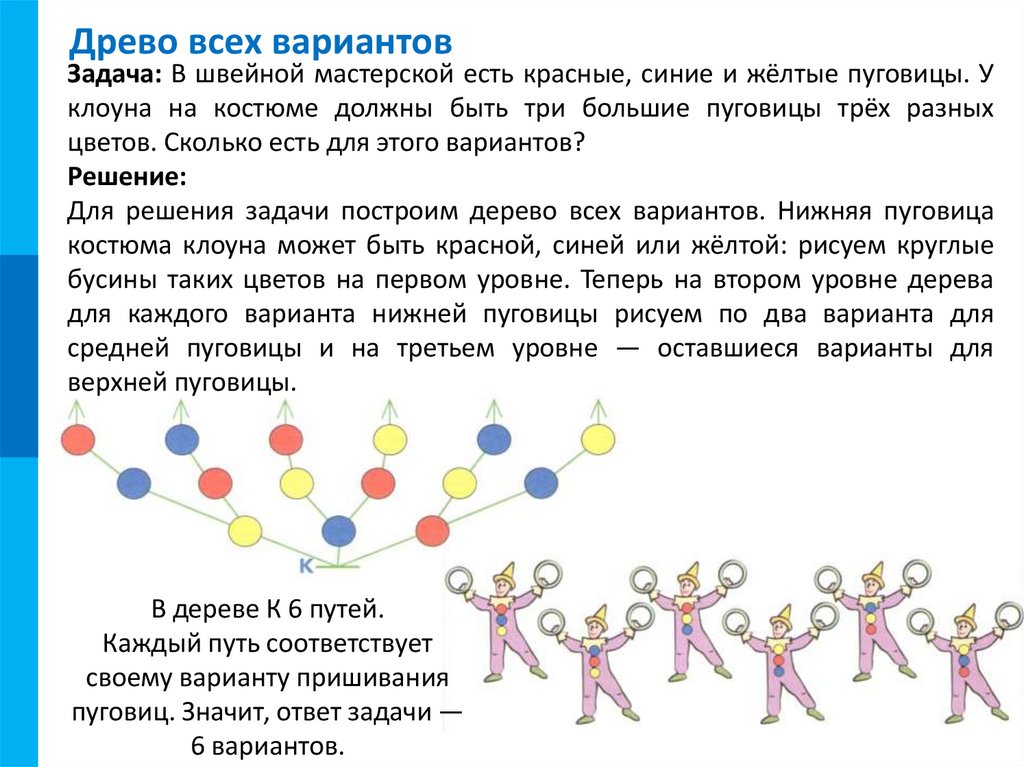
Задача: В швейной мастерской есть красные, синие и жёлтые пуговицы. У
клоуна на костюме должны быть три большие пуговицы трёх разных
цветов. Сколько есть для этого вариантов?
Решение:
Для решения задачи построим дерево всех вариантов. Нижняя пуговица
костюма клоуна может быть красной, синей или жёлтой: рисуем круглые
бусины таких цветов на первом уровне. Теперь на втором уровне дерева
для каждого варианта нижней пуговицы рисуем по два варианта для
средней пуговицы и на третьем уровне — оставшиеся варианты для
верхней пуговицы.
В дереве К 6 путей.
Каждый путь соответствует
своему варианту пришивания
пуговиц. Значит, ответ задачи —
6 вариантов.
4.
МКРассматривая задачу, можно сделать
следующий вывод:
- на первом уровне дерева мы помещаем все элементы, которые
могут быть первыми в искомых последовательностях;
- на втором уровне для каждого из элементов первого уровня мы
рисуем следующие вершины—элементы, которые могут стоять
вторыми в последовательности, при условии что первым выбран
данный элемент;
- затем рисуем следующие за элементами второго уровня—
элементы, которые могут стоять третьими, при условии что первым
и вторым выбраны данные элементы.
Так мы двигаемся, пока число уровней не станет равно длине
искомой последовательности. В результате получаем дерево
перебора—дерево, все пути которого представляют собой искомые
последовательности.
Выписав их, получаем множество вариантов.
5.
МКСамостоятельная работа
№1. Мальчишки соревновались в стрельбе по воздушным шарикам из
самодельного лука. Шарики были трёх цветов: зелёные, синие и красные,
по 4—5 штук каждого цвета. Петя выстрелил два раза и оба раза попал: два
синих шарика лопнули. В шарики каких цветов он мог бы попасть, сделав
два точных выстрела?
№2. Выясни, сколько можно построить разных цепочек длины
3, используя только такие бусины, которые есть в мешке А.
№3. В харчевне «Три пескаря» на первое предлагали борщ и уху, на второе
— стейк из свинины, рыбные котлеты и овощное рагу, на десерт —
мороженое. Каждый обед должен состоять из одного первого блюда,
одного второго и десерта, при этом в обеде не должно быть больше одного
рыбного блюда. Сколько вариантов таких обедов можно получить из этого
набора блюд?




 informatics
informatics








