Автоматика и управление. Тема 7. Синтез линейных стационарных автоматических систем

1.

Автоматика и управление
Тема 7. Синтез линейных
стационарных автоматических систем
Лекция 8. Общая и частная задачи синтеза. Выбор параметров
АС по минимуму ИКО. Метод стандартных коэффициентов.
Последовательные и параллельные корректирующие
устройства (КУ).

2.

7.1. Общая и частная задачи синтеза АС
В ТАУ синтез АС - это процесс определения структуры, состава элементов
и значений параметров АС, при которых она удовлетворяет
предъявляемым к ней требованиям.
Методика решения общей задачи синтеза АС:
1. Составляется функциональная схема АС.
2. Выбираются функционально необходимые элементы АС с учетом
обеспечения энергетических, эксплуатационных и других требований.
3. Определяются математические модели и передаточные функции
элементов АС и составляется ее структурная схема.
4. Производится оценка качества процесса управления выбранной АС. Если
качество процесса управления удовлетворяет заданным требованиям задача синтеза АС решена.
5. Если заданные требования не выполняются, то улучшают качество АС
изменением в допустимых пределах параметров элементов АС.
6. Если изменением параметров невозможно добиться удовлетворения
требований, то в структуру АС включают корректирующее устройство (КУ).
Задача определения параметров элементов АС или структуры и
параметров КУ, обеспечивающих заданные требования к АС с известной
структурой, называется частной задачей синтеза АС

3.

7.2. Выбор параметров АС по минимуму интегральной
квадратичной оценки
Постановка задачи:
Известны структура АС и, следовательно, ее передаточная функция
Ф (p, К1 ,К2 ,...). Параметры АС Кi могут изменяться в диапазонах, заданных
конструктором.
Дана желаемая переходная функция hж(t) АС такая, что ее изображение по
Лапласу есть рациональная функция L[hж(t)]=Hж(P).
Требуется выбрать такие параметры АС Ki, чтобы они обеспечивали
минимум ИКО:
2
I = [h ж (t) - h(t, K 1 , K 2 ,...)] dt =Imin (K1 ,K2,...)
0

4.

Допустим, необходимо выбрать только один параметр K1, а остальные
заданы и имеют конкретные числовые значения.
1. По заданной hж(t) определяют ее изображение Hж(p).
А) Если система должна обладать максимальным быстродействием, то в
качестве hж(t) берут ступенчатую функцию:
hж(t)= h( )1(t) = Ф(0)1(t) - для статических АС,
hж(t)= 1(t) - для астатических следящих систем (так как h( )=1, потому что
а0 =в0 ).
Недостаток - малая степень устойчивости, т.е. большое перерегулирование
hm АС, рассчитанной по минимуму ИКО.
-t/T
Б) hж(t)= 1-е
Т выбирается из условия 3T = tp, tp - желаемое время
регулирования
2. Составляют аналитическое выражение для заданной ИКО
B
I = [h ж (t) - h(t, K 1 )] 2 dt I[H ж (p) - H(p, K 1 )]
2a n
0
, В= f(K1 ), то есть I = I(K1 )

5.

3. Определяют значения K1, при которых ИКО имеет экстремумы.
dI ( K 1 )
0.
dK 1
4. Определяют какое из найденных значений K1 соответствует минимуму
ИКО
d 2 I( K1 )
0.
2
dK 1
При выборе нескольких параметров K1, K2,... по минимуму ИКО
После определения ИКО, как функции нескольких параметров I=I(K1,K2 ,...),
вычисляют и приравнивают нулю ее частные производные по каждому из
варьируемых параметров Ki:
I ( K 1 , K 2 ,...)
0,
Ki
i=1,2,…
Полученная система алгебраических уравнений позволяет вычислить
искомые значения параметров Ki, при которых функция I=I(K1,K2 ,...)
достигает экстремумов.

6.

Проверить, действительно ли найденные значения Ki соответствуют
минимуму ИКО.
d 2 I ( K 1 , K 2 ...)
0,
2
dK 1
Целесообразно применять для систем не выше третьего порядка.

7.

7.3 Метод стандартных коэффициентов
Метод стандартных коэффициентов (МСК) предполагает такой выбор
параметров элементов АС (Т, , К, …) при котором коэффициенты
передаточной функции системы аi, вi принимают заранее назначенные
(стандартные) значения. При этом и график переходной функции системы
h(t) будет иметь желаемую (стандартную) форму с требуемыми
показателями качества.
Синтез статических АС
Пусть передаточная функция разомкнутого контура статической системы
W( p )
K
a n p a n 1 p
p
p 1
... a1 p 1
,
Необходимо определить такие значения K и ai, i=1, n , при которых
замкнутая АС будет отвечать заданным требованиям качества: tp - времени
регулирования; е(t) - ошибке в установившемся режиме. Перерегулирование
hm в случае синтеза АС МСК, как правило, ограничено не более 5%.

8.

Численное значение коэффициента усиления K определяется из требований
к величине ошибки АС в установившемся режиме e(t) или, что тоже самое, к
величине коэффициента статизма системы S0. Известно, что если
x(t)=const, то справедливы равенства:
e(t)=S0x(t), S0
Из формулы лекции 10
1
S0
K 1
e( t )
;
x( t )
1 S0
K
.
S0
Коэффициенты ai выбираются исходя из требований к величине времени
регулирования tp по таблице
n
n pi
i 1
среднегеометрический
корень системы, где
pi - модули корней
характеристического
уравнения A(p) = 0.

9.

1. По заданной ошибке в установившемся режиме e(t) или коэффициенту
статической точности S0 определяют величину коэффициента усиления
системы K:
x(t ) e(t )
K
e(t )
1 S0
K
S0
2. Вычисляют значение среднегеометрического корня системы для
заданного времени регулирования tp и порядка системы n:
t p
где величина tp определяется из табл. в соответствии со
tp
значением n.
3. Вычисляют стандартные значения коэффициентов ai по соответствующим
формулам таблицы. Записывают передаточную функцию W(p) разомкнутой
системы со стандартными коэффициентами ai
4. Определяют необходимые значения параметров элементов АС Tk, Kk
путем приравнивания коэффициентов при равных степенях p знаменателей
~
передаточных функций W(p) и W
( p)
а~i (T , K ) = a , i =1,n
k
k
i
5. Выясняют возможность физической реализации необходимых значений
параметров Tk,и Kk. Если их точная реализация невозможна, то выбирают
граничные значения параметров, близкие к необходимым.

10.

Синтез астатических АС
Синтез астатических АС отличается лишь формулами вычисления
коэффициентов ai и K, причем, для систем с различным порядком
астатизма формулы расчета ai различны
Для систем первого порядка астатизма ( =1), передаточная функция
разомкнутого контура которых, имеет вид:
K
W ( p)
p (an p n 1 a2 p 1)

11.

Коэффициент усиления разомкнутой системы K рассчитывается одним из
двух путей, в зависимости от первоочередности таких показателей качества,
как точность и быстродействие АС:
1. Астатическая точность:
Задана величина допустимой ошибки e(t) в установившемся режиме,
при известной максимальной скорости изменения задающего воздействия
x(1)(t). Тогда
e(t) = S1
x(1)(t),
S1
1
S1 ,
K
e( t )
(1)
xmax
(t )
1
K
S1
Формула из лекции 10
(1)
x max
K
e( t )
Вычисленное значение K, по таблице для АС n-го порядка, определит
величины и tp .

12.

2. Быстродействие АС:
Задано время регулирование tp. Вычисляется = tp /tp , где произведение
tp выбирается из табл. при известном порядке синтезируемой системы n.
Тогда K определится из той же таблицы.
В остальном порядок расчета астатической системы не отличается от
порядка расчета статической системы.
Основным достоинством метода стандартных коэффициентов является
его относительная простота.

13.

К недостаткам метода, ограничивающим его широкое применение,
можно отнести:
1. Вычислительные трудности, возникающие при решении нелинейных
алгебраических уравнений от второго порядка и выше при синтезе систем
третьего порядка и выше, соответственно.
2. Для системы n-го порядка одновременно выбирают n параметров, т.е.
необходимо решать систему из, по крайней мере, n нелинейных уравнений с
n варьируемыми параметрами, а с учетом коэффициентов числителя
передаточной функции W(p), вi , i 1, m , то и того больше, что не всегда
возможно.
3. Вычисляемые значения параметров K и ai не всегда могут быть
физически реализованы, прежде всего из-за ограничения по
перерегулированию для стандартных переходных функций.
Метод Лина
Метод Лина позволяет раскладывать полиномы A(p) третьего порядка и
выше на элементарные множители, вида (Tip+1) и ( p2+2Tj j p+1), j <1.
Применение метода Лина уменьшает вычислительные трудности,
возникающие при синтезе АС методом стандартных коэффициентов,
облегчает задачу анализа устойчивости АС по корням характеристического
уравнения.

14.

7.4 Последовательные (П-, ПИ-, и ПИД- регуляторы) и
параллельные корректирующие устройства (КУ)
При решении частной задачи синтеза, АС может быть
представлена в виде "неизменной части" системы и
корректирующих устройств (КУ), заданных передаточными
функциями WН (p) и WKi(p), соответственно.
X(p)
WK1(p)
WН(p)
WK2(p)
Корректирующим устройством называется
вспомогательный элемент АС, применяемый для
улучшения качества ее процессов управления.
Y(p)

15.

Последовательным называется КУ, включенное в
прямой тракт передачи сигнала управления WК1(p).
Параллельное КУ WK2 (p) включается в обратную связь
внутреннего контура.
Таким образом, задача синтеза АС при помощи введения в ее
состав корректирующих устройств по существу сводится к
выбору типа и параметров КУ, при которых АС отвечает
заданным показателям качества. Поэтому часто вместо
термина "синтез АС", употребляют термин "синтез
корректирующего устройства".

16.

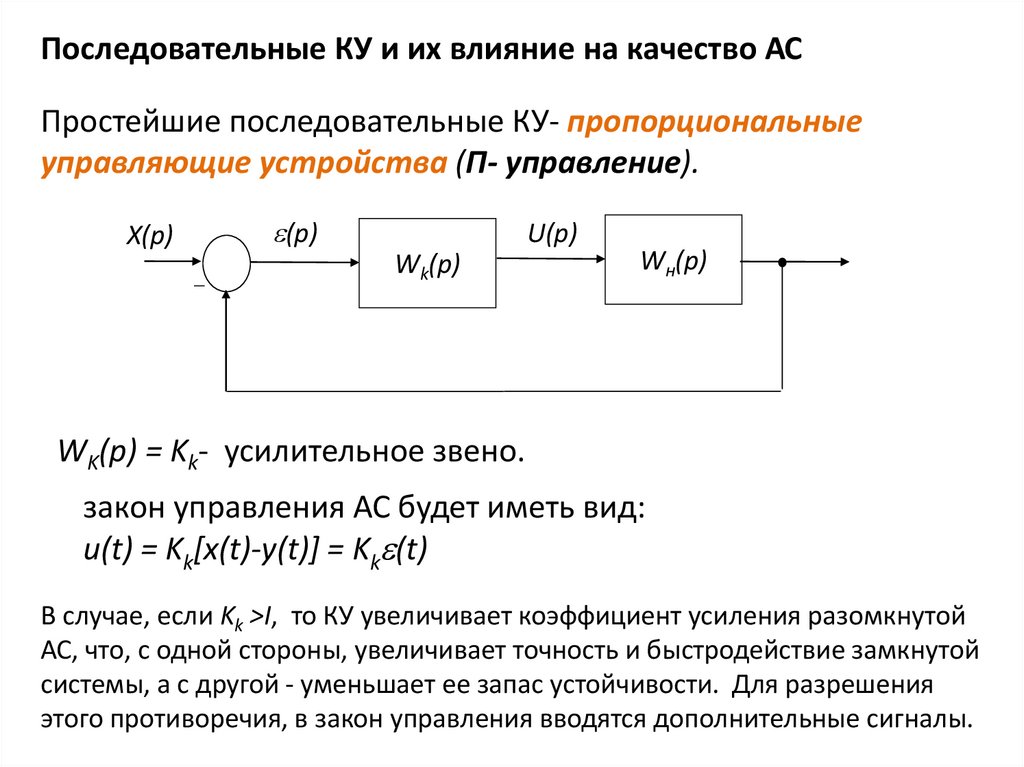
Последовательные КУ и их влияние на качество АС
Простейшие последовательные КУ- пропорциональные
управляющие устройства (П- управление).
X(p)
(p)
U(p)
Wk(p)
Wн(p)
WK(p) = Kk- усилительное звено.
закон управления АС будет иметь вид:
и(t) = Kk[x(t)-у(t)] = Kk (t)
В случае, если Kk >I, то КУ увеличивает коэффициент усиления разомкнутой
АС, что, с одной стороны, увеличивает точность и быстродействие замкнутой
системы, а с другой - уменьшает ее запас устойчивости. Для разрешения
этого противоречия, в закон управления вводятся дополнительные сигналы.

17.

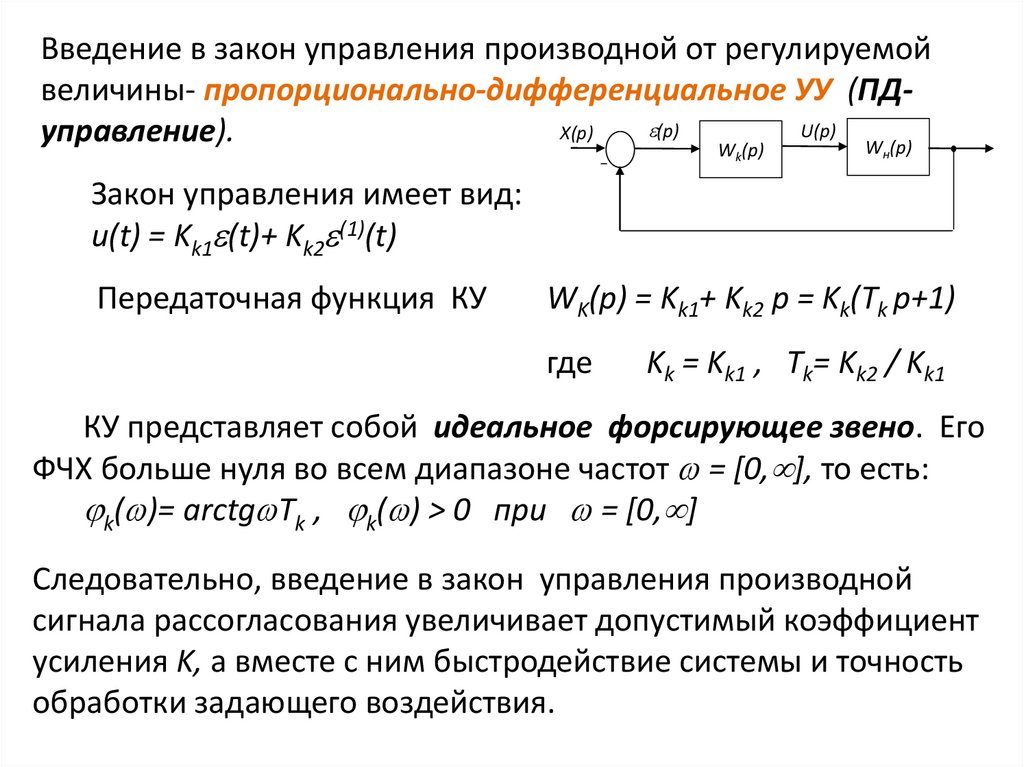
Введение в закон управления производной от регулируемой
величины- пропорционально-дифференциальное УУ (ПДU(p)
(p)
X(p)
управление).
W (p)
W (p)
k
н
Закон управления имеет вид:
u(t) = Kk1 (t)+ Kk2 (1)(t)
Передаточная функция КУ
WK(p) = Kk1+ Kk2 p = Kk(Tk p+1)
где
Kk = Kk1 , Tk= Kk2 / Kk1
КУ представляет собой идеальное форсирующее звено. Его
ФЧХ больше нуля во всем диапазоне частот = [0, ], то есть:
k( )= arctg Tk , k( ) > 0 при = [0, ]
Следовательно, введение в закон управления производной
сигнала рассогласования увеличивает допустимый коэффициент
усиления K, а вместе с ним быстродействие системы и точность
обработки задающего воздействия.

18.

Идеальное форсирующее звено относится к разряду физически
нереализуемых звеньев. Поэтому, в качестве
фазоопережающего КУ выбирают "реальное" форсирующее
звено:
TК 1 p 1
TK 2
WК ( p) K К
TК 2 p 1 где TK1 >TK2, KK = TK 1 < 1
к,,
Расчеты показывают, что максимум
функции K( ) достигается на частоте
Lк,дб
град
T 1
90 20
1=1/Tк1
100
0,1
1
-90
10
-20
Т
1000
Т К 1Т К 2
,с-1
2=1/Tк2
совпадающей в логарифмическом
масштабе с серединой интервала частот
(1/ TK1, 1/ TK2).

19.

Частоту T КУ выбирают так, чтобы она совпадала с частотой среза c
“неизменной” части АС. Это позволяет либо увеличить запас устойчивости
по фазе скорректированной системы, либо, при заданном запасе
устойчивости по фазе, увеличить ее коэффициент усиления и тем самым
быстродействие и точность.
Недостаток–
Если корректируемый сигнал представляет собой
значительно
напряжение электрического тока, то в качестве реального усиливает
форсирующего звена обычно выбирают пассивный
высокочастотные
четырехполюсник.
помехи (шумы) АС.
C
При отсутствии нагрузки на выходе
четырехполюсника (RH= ):
(t )
(t )( R1Cj 1) R2
u (t ) i (t ) R2
R2
(t)
u(t)
R1 1 / Cj
R2 R1Cj R2 R1
R2
R1 1 / Cj
K (T p 1)
АФЧХ четырехполюсника имеет вид
WK ( p ) K K 1
(TK 2 p 1)
( R1Cj 1 )R2
u( j )
W K ( j )
.
R2
KK
( j ) R2 R1Cj R2 R1
R1
R2
передаточная функция
( R1Cp 1) R2
W
(
p
)
K
пассивного КУ
R R Cp R R
2 1
2
1
R2 R1
TK1=R1C
TK2=
R2 R1C
R2 R1

20.

Введение в закон управления интеграла от регулируемой
величины- пропорционально-интегральное УУ – (ПИуправление)
t
Закон управления
u(t) = K1ε(t) + K2
( )dt
0
1 K K (TK p 1)
p
p
KK = K2, TK= K1/K2
WK ( p) K1 K 2
Передаточная функция КУ
где
Введение интегрирующих звеньев в передаточную функцию разомкнутой
системы увеличивает ее точность в установившемся режиме, но при этом
уменьшается запас устойчивости АС
АЧХ и ФЧХ КУ
WaK ( ) K
2
1
K 22
2
K( )= - /2 + arctgTK
Так как ФЧХ КУ во всем диапазоне частот =[0, ] меньше нуля: K( ) < 0 ,
[0 ], то запас устойчивости АС уменьшается.
C увеличением частоты величина АЧХ КУ уменьшается, то есть КУ может
быть использовано для подавления сигналов высокой частоты (помехи высокочастотные).

21.

Для исключения вредного влияния интеграла в законе управления на запас
устойчивости АС по фазе, на практике используют КУ, передаточная функция
которого представляет собой обращенное «реальное» форсирующее звено:
WK ( p )
к,,
град
/2
TK 2 p 1
TK 1 p 1
TK1 >TK2
Lк,дб
T
20
0
1
1
Т
10
100
2
1
TK 1TK 2
1000
,с-1
-20
Для того, чтобы данное КУ не уменьшало запас устойчивости
АС по фазе, частоту T выбирают существенно меньшей частоты
среза c неизменяемой части АС:
T << c.

22.

КУ может быть реализовано пассивным четырехполюсником
тока:
R1
(t)
C
R2
u(t)

23.

Пропорционально- интегральнодифференциальное управление-(ПИД- регулятор)
ПИД- регулятор представляет собой последовательное КУ,
объединяющее достоинства ПИ- и ПД- регуляторов, причем частоты
ТПИ и ТПД выбираются в соответствии с неравенствами:
ТПИ << C , а ТПД >> C.
При соблюдении данных неравенств АС с ПИД- регулятором будет
иметь достаточно большой запас по фазе З и низкий уровень
широкополосных помех при заданной точности. Либо, при заданном
З можно существенно увеличить К системы, а тем самым уменьшить
ее ошибку е(t) в установившемся режиме.
Для устойчивого объекта можно выбрать коэффициенты регулятора
опытным путем, выполняя эксперименты с реальным объектом.
Предложено несколько методов решения этой задачи, например,
правила Зиглера-Никольса или Коэна-Куна.

24.

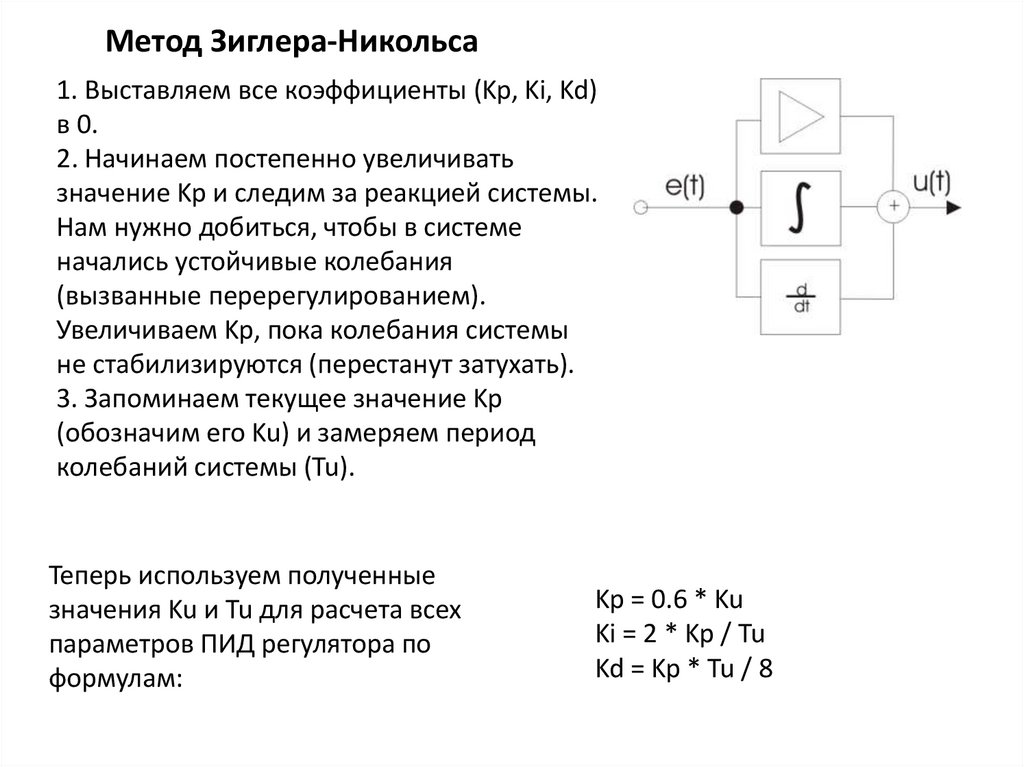
Метод Зиглера-Никольса
1. Выставляем все коэффициенты (Kp, Ki, Kd)
в 0.
2. Начинаем постепенно увеличивать
значение Kp и следим за реакцией системы.
Нам нужно добиться, чтобы в системе
начались устойчивые колебания
(вызванные перерегулированием).
Увеличиваем Kp, пока колебания системы
не стабилизируются (перестанут затухать).
3. Запоминаем текущее значение Kp
(обозначим его Ku) и замеряем период
колебаний системы (Tu).
Теперь используем полученные
значения Ku и Tu для расчета всех
параметров ПИД регулятора по
формулам:
Kp = 0.6 * Ku
Ki = 2 * Kp / Tu
Kd = Kp * Tu / 8