Задачи на сплавы. Часть 1

1.

Математика
Преподаватель высшей категории
Анисимова Оксана Михайловна
ВИФК Кадетский корпус (спортивная школа)

№1
Решение задач «задание 11»
В сосуд, содержащий 5 литров 14-процентного водного
раствора некоторого вещества, добавили 5 литров воды.
Сколько процентов составляет концентрация
получившегося раствора?
всего
концентрац
ия
Масса
вещества
5
5
5+5=10
14%
?
0,14 5 0,7
??
Было
Добавили
стало
mk
cm
100%
m0
0,7
cm
100% 7%
10
0,7
Ответ: 7

3.

№2
Решение задач «задание 11»
Смешали некоторое количество 15-процентного раствора
некоторого вещества с таким же количеством 17процентного раствора этого вещества. Сколько
процентов составляет концентрация получившегося
раствора?
??
I
II
I+II
всего
концентрация
Масса вещества
x
15%
0,15x
x
2x
17%
?
0,17x
0,15x + 0,17x = 0,32x
mk
cm
100%
m0
0,32 x
cm
100% 16%
2x
Ответ: 16

4.

№3
Решение задач «задание 11»
Смешали 4 литра 20-процентного водного раствора
некоторого вещества с 6 литрами 35- процентного
водного раствора этого же вещества. Сколько процентов
составляет концентрация получившегося раствора?
??
I
II
I+II
всего
концентрация
Масса вещества
4
20%
0,2·4=0,8
6
4+6=10
35%
?
0,35·6=2,1
0,8 + 2,1 = 2,9
mk
cm
100%
m0
2,9
cm
100% 29%
10
Ответ: 29

5.

№4.1
Решение задач «задание 11»
Имеется два сплава. Первый содержит 10% никеля,
второй — 35% никеля. Из этих двух сплавов получили
третий сплав массой 150 кг, содержащий 30% никеля. На
сколько килограммов масса первого сплава была меньше
массы второго?
??
I
II
I+II
всего
концентрация
Масса вещества
x
y
150
10%
35%
30%
0,1x
0,35y
0,3·150=45
0,1x+0,35y=45
x y 150
x 150 y
x 30
0,1x 0,35 y 45 0,1(150 y ) 0,35 y 45
Ответ: 90
y 120

6.

№4.2
Решение задач «задание 11»
Имеется два сплава. Первый содержит 20% никеля,
второй — 45% никеля. Из этих двух сплавов получили
третий сплав массой 90 кг, содержащий 30% никеля. На
сколько килограммов масса первого сплава была больше
массы второго?
??
I
всего
концентрация
Масса вещества
x
y
90
20%
45%
30%
0,2x
0,45y
0,3·90=27
0,2x+0,45y=27
II
I+II
x y 90
x 54
x 90 y
0,2 x 0,45 y 27 0,2(90 y ) 0,45 y 27
Ответ: 18
y 36

7.

Решение задач «задание 11»
№5
Численность волков в двух заповедниках составляла 210
особей. Через год обнаружили, что в первом заповеднике
численность волков возросла на 10%, а во втором — на
30%. В результате общая численность волков в двух
заповедниках составила 251.Сколько волков было в
первом из заповедников первоначально?
??
I
II
I+II
Первый год
Второй год
x
y
210
x+0,1x
y+0,3y
251
x y 210
1,1x 1,3 y 251
y 210 x
x 110
0,1x 0,3(210 x) 251
y 100
Ответ: 110

8.

№6.1
Решение задач «задание 11»
Имеется два сплава. Первый сплав содержит 5% меди,
второй — 14% меди. Масса второго сплава больше массы
первого на 9 кг. Из этих двух сплавов получили третий
сплав, содержащий 11% меди. Найдите массу третьего
сплава. Ответ дайте в килограммах.
??
I
II
I+II
всего
Процентное
содержание
Масса вещества
x
x+9
5%
14%
0,05x
0,14(x+9)
2x+9
11%
0,11(2x+9)=
0,05x+0,14(x+9)
0,11(2 x 9) 0,05 x 0,14( x 9)
0,03x 0,27
x 9
Ответ: 27

9.

№6.2
Решение задач «задание 11»
Имеется два сплава. Первый сплав содержит 10% меди,
второй — 40% меди. Масса второго сплава больше массы
первого на 3 кг. Из этих двух сплавов получили третий
сплав, содержащий 30% меди. Найдите массу третье го
сплава. Ответ дайте в килограммах.
??
I
II
I+II
всего
Процентное
содержание
Масса вещества
x
x+3
10%
40%
0,1x
0,4(x+3)
2x+3
30%
0,3(2x+3)=
0,1x+0,4(x+3)
0,3(2 x 3) 0,1x 0,4( x 3)
Ответ: 9

10.

№7.1
Решение задач «задание 11»
Смешав 6-процентный и 74-процентный растворы кислоты и
добавив 10 кг чистой воды, получили 19-процентный раствор
кислоты. Если бы вместо 10 кг воды добавили 10 кг 50процентного раствора той же кислоты, то получили бы 24процентный раствор кислоты. Сколько килограммов 6процентного раствора использовали для получения смеси?
Процент
всего
Масса вещества
??
I
II
Получили 1 раз
x
y
10
x+y+10
6%
74%
19%
0,06x
0,74y
0.19(x+y+10)=
=0,06x+0,74y
Добавили 2раз
10
50%
0,5·10=5
Получили 2 раз
x+y+10
24%
0.24(x+y+10)=
=0,06x+0,74y+5
Добавили 1 раз

11.

№7.1
Решение задач «задание 11»
всего
??
I
Процент
Масса вещества
Получили 1 раз
x
y
10
x+y+10
6%
74%
19%
0,06x
0,74y
0.19(x+y+10)=
=0,06x+0,74y
Добавили 2раз
10
50%
0,5·10=5
Получили 2 раз
x+y+10
24%
0.24(x+y+10)=
=0,06x+0,74y+5
II
Добавили 1 раз
0,19( x y 10) 0.06 x 0.74 y
0,24( x y 10) 0.06 x 0.74 5

12.

№7.1
Решение задач «задание 11»
0,19( x y 10) 0.06 x 0.74 y
0,24( x y 10) 0.06 x 0.74 y 5
0.05( x y 10) 5
x y 10 100
0,19( x y 10) 0.06 x 0.74 y
x y 10 100
19 0.06 x 0.74 y
19 0.06 x 0.74(90 x)
x y 10 100
y 90 x
x 70
y 20
Ответ: 70

13.

Самостоятельно
Сборник «4000 задач»
№1586,
№1590
№ 1587,
№11 вариант1
№11 вариант2

14.

15.

№1.1
Решение задач «задание 11»
Объем
работы
I
Производительно
сть (скорость)
20
x+4
60
x
II
время
20
8
x 4
60
x
20
60
8
x 4
x
x 2 x 30 0
Ответ: 6

16.

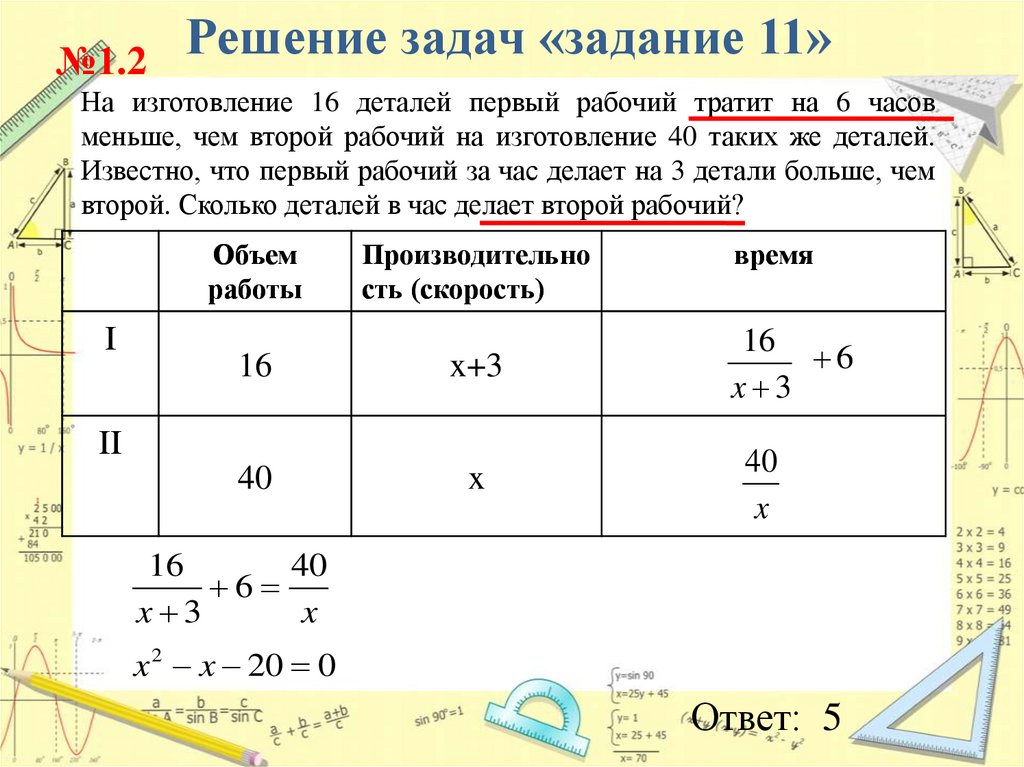
№1.2
Решение задач «задание 11»
На изготовление 16 деталей первый рабочий тратит на 6 часов
меньше, чем второй рабочий на изготовление 40 таких же деталей.
Известно, что первый рабочий за час делает на 3 детали больше, чем
второй. Сколько деталей в час делает второй рабочий?
Объем
работы
I
Производительно
сть (скорость)
16
x+3
40
x
II
время
16
6
x 3
40
x
16
40
6
x 3
x
x 2 x 20 0
Ответ: 5

17.

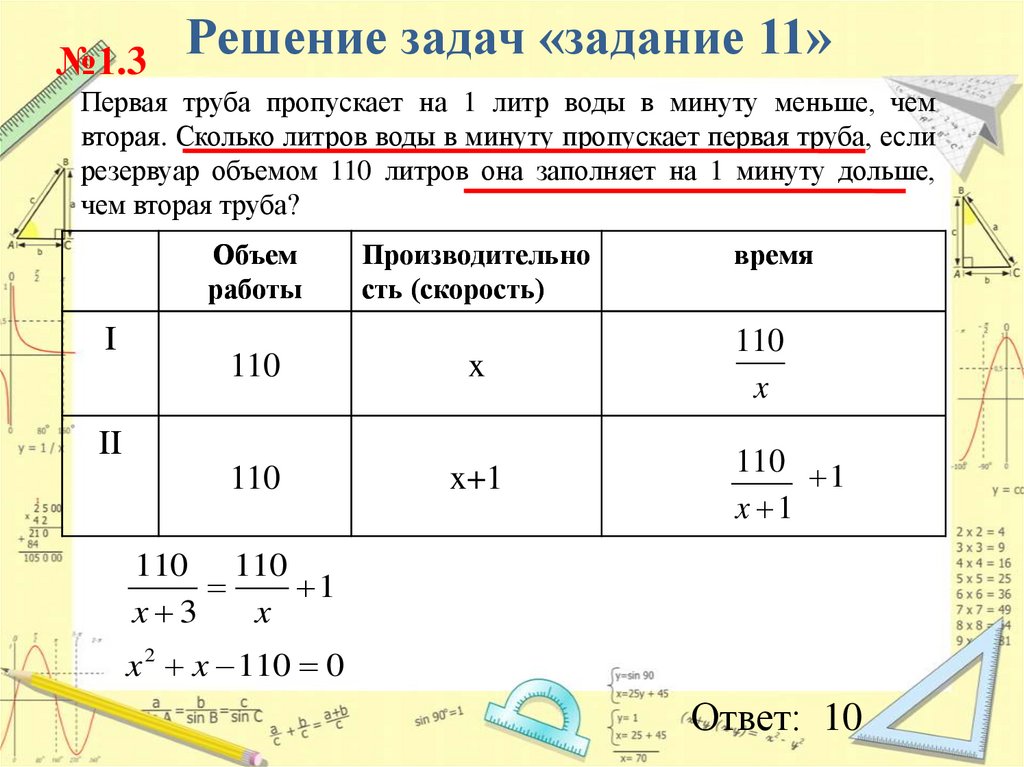
№1.3
Решение задач «задание 11»
Первая труба пропускает на 1 литр воды в минуту меньше, чем
вторая. Сколько литров воды в минуту пропускает первая труба, если
резервуар объемом 110 литров она заполняет на 1 минуту дольше,
чем вторая труба?
Объем
работы
I
Производительно
сть (скорость)
110
x
110
x+1
II
время
110
x
110 1
x 1
110 110
1
x 3
x
x 2 x 110 0
Ответ: 10

18.

№2.1
Решение задач «задание 11»
Объем работы
V t
I
II
Производительность
(скорость)
время
12y·10
12y
10
24yx
12y+12y
X
21y·10
21y
10
9yx
21y-12y=9y
X
120 y 24 yx 210 y 9 yx
15 yx 90 y
x 6
Ответ: 16

19.

№2.2
Решение задач «задание 11»
Две бригады, состоящие из рабочих одинаковой квалификации,
одновременно начали выполнять два одинаковых заказа. В первой
бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней
после начала работы в первую бригаду перешли 8 рабочих из второй
бригады. В итоге оба заказа были выполнены одновременно. Найдите,
сколько дней потребовалось на выполнение заказов.
Объем работы
I
II
V t
16y·7=112y
Производительность
(скорость)
время
16y
7
24yx
16y+8y=24y
X
25y·7=175y
25y
7
17yx
25y-8y=17y
X
112 y 24 yx 175 y 17 yx
7 yx 63 y
x 9
Ответ: 16

20.

Самостоятельно
Сборник «4000 задач»
№ 1639
№1652
№1622

21.

Интернет ссылки

English Русский Rules