Сложение вероятностей. 11 класс

1.

11 класс
Алгебра
МКОУ
Букановская средняя школа

2.

говорят, что
вероятность встать
НЕ С ТОЙ НОГИ, больше у
сороконожки

3.

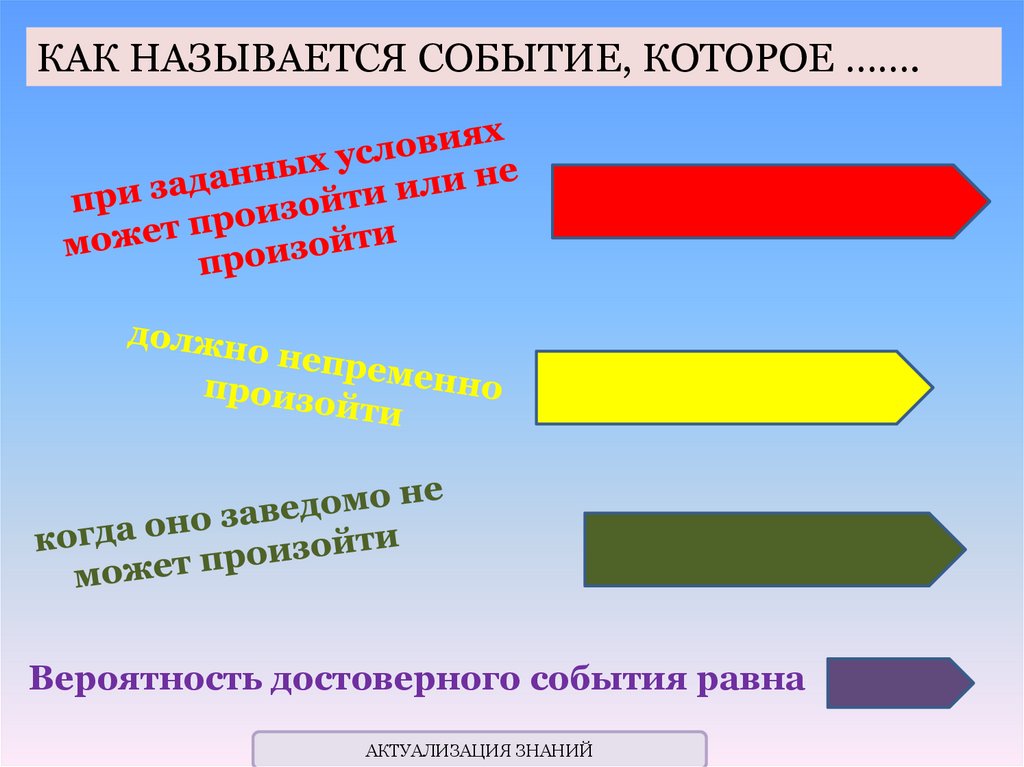
КАК НАЗЫВАЕТСЯ СОБЫТИЕ, КОТОРОЕ …….
СЛУЧАЙНЫМ
ДОСТОВЕРНЫМ
НЕВОЗМОЖНЫМ
Вероятность достоверного события равна
АКТУАЛИЗАЦИЯ ЗНАНИЙ
1

4.

КАК НАЗЫВАЮТСЯ СОБЫТИЯ, ЕСЛИ…….
НЕСОВМЕСТНЫМИ
СОВМЕСТНЫМИ
если в условиях испытания они, являясь
единственными его исходами,
несовместны.
ПРОТИВОПОЛОЖНЫМИ
АКТУАЛИЗАЦИЯ ЗНАНИЙ

5.

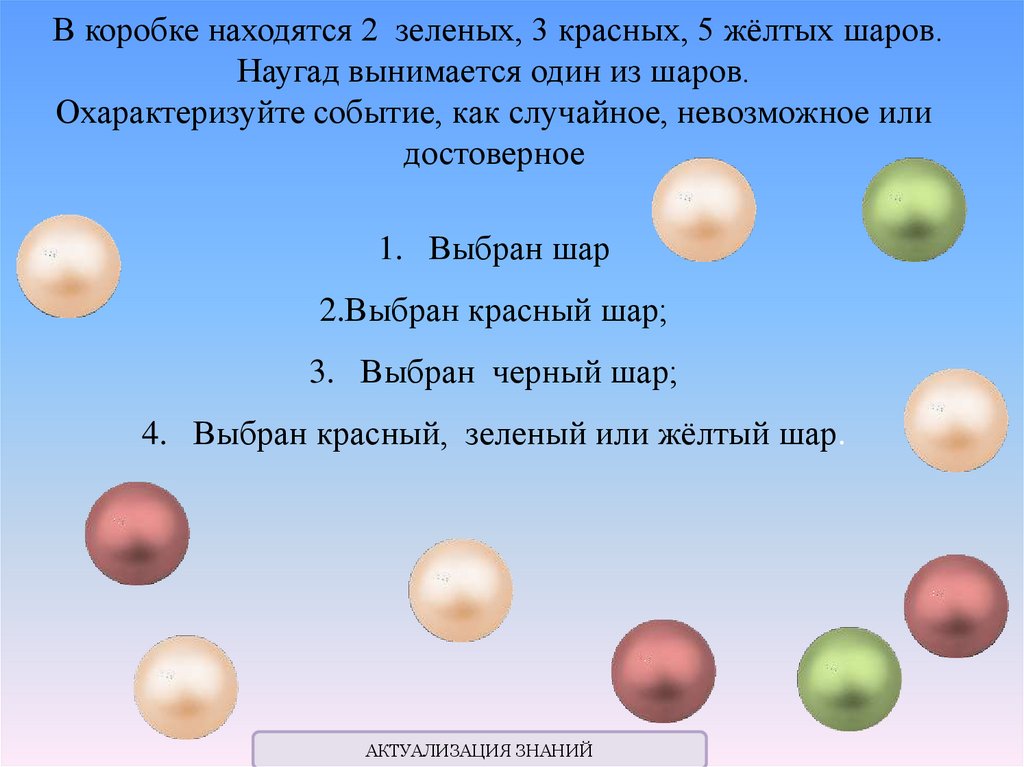
В коробке находятся 2 зеленых, 3 красных, 5 жёлтых шаров.
Наугад вынимается один из шаров.
Охарактеризуйте событие, как случайное, невозможное или
достоверное
1. Выбран шар
2.Выбран красный шар;
3. Выбран черный шар;
4. Выбран красный, зеленый или жёлтый шар.
АКТУАЛИЗАЦИЯ ЗНАНИЙ

6.

Назовите событие противоположное данному:
1. студент сдаст зачет;
2. попадание при выстреле;
3. выпадение орла при одном броске
Среди событий, связанных с одним
бросанием игральной кости найти пары совместных
и пары несовместных событий.:
1) выпало 2 очка; 2) выпало 5 очков; 3) выпало более 2 очков ;
4) выпало число очков, кратное двум
Совместные 3 пары : 1и 4;
Несовместные 3 пары : 1 и 2;
2 и 3;
1 и 3;
АКТУАЛИЗАЦИЯ ЗНАНИЙ
3и4.
2 и 4.

7.

Что изображено с помощью кругов Эйлера?
Опишите, в чем состоит сумма следующих
несовместных событий:
а). Учитель вызвал к доске ученика (событие А), ученицу
(событие В).
Произведение
Событие,
Сумма событий
б). «Родила царица в ночь,
не то сына (А), не
то дочь (В)…».
событий
противоположное
событию
А, 6 (В).
в). Случайно выбранная цифра меньше 5 (А),
больше
Решение: а). Учитель вызвал к доске ученика или ученицу (А илиВ).
б). Царица родила сына или дочь (А илиВ).
в). Случайно выбранная цифра меньше 5 или больше 6 (А или В, то есть это
одна из цифр 0,1,2,3,4,5,6,7,8,9).

8.

В жеребьевке участвуют 5 немцев, 8 французов и 3 эстонца.
Какова вероятность того, что первым
/вторым/седьмым/последним – не важно) будет выступать
француз
Когда подбрасываем монету, какова вероятность выпадения
решки?
В ящике
10 шаров:монету
3 синих,
6 белых,
остальные
красные.
А если
подбрасываем
два
раза? Какова
вероятность
Наугад
(нераза
глядя)
достаём
один из них. Какова вероятность
того,
что оба
выпадет
орел?
того, что выбранный таким образом шар окажется белого
цвета?
Какова вероятность того, что выбранный таким образом шар
окажется цветным? (не белый)
АКТУАЛИЗАЦИЯ ЗНАНИЙ

9.

1 группа: Бросаем один раз
игральный кубик. Какова вероятность
выпадения на нем двух или пяти
очков?
РАБОТА
В
ГРУППАХ
2 группа: Бросаем один раз игральный
кубик. Вероятность выпадения четного
количества очков равна 0, 52. Найдите
вероятность выпадения на нем нечетного
количества очков.
3 группа: Бросаем, один раз,
два игральных кубика. Какова
вероятность выпадения на них
двух или пяти очков?

10.

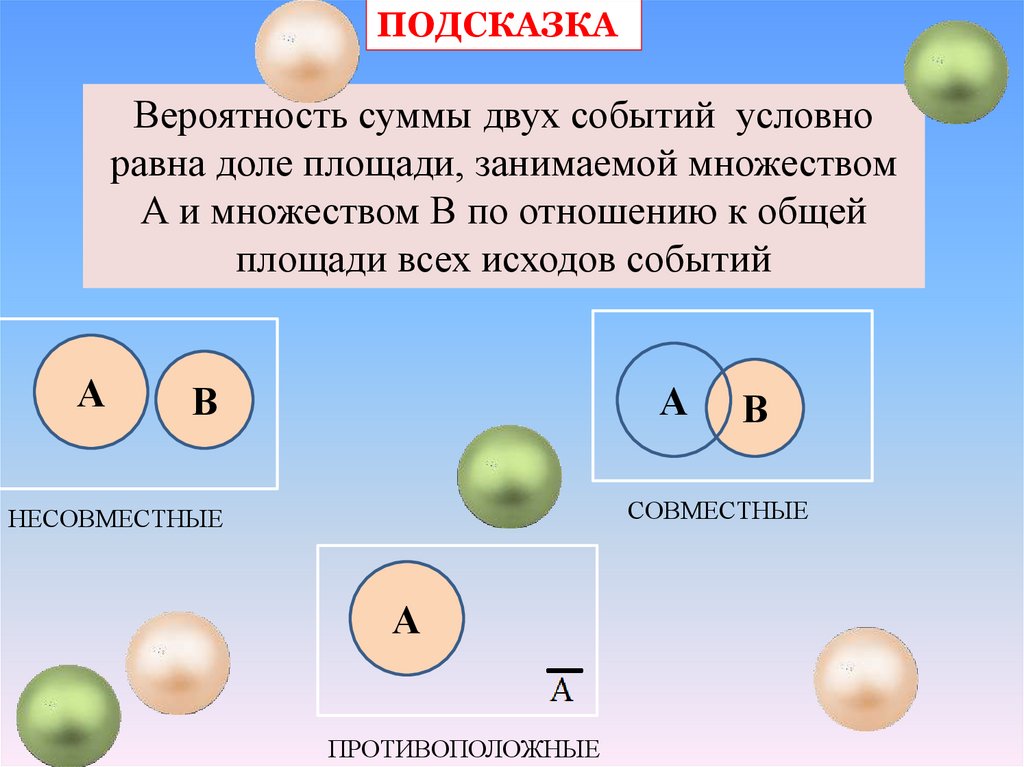
ПОДСКАЗКА
Вероятность суммы двух событий условно
равна доле площади, занимаемой множеством
А и множеством В по отношению к общей
площади всех исходов событий
А
В
А
В
СОВМЕСТНЫЕ
НЕСОВМЕСТНЫЕ
А
ПРОТИВОПОЛОЖНЫЕ

11.

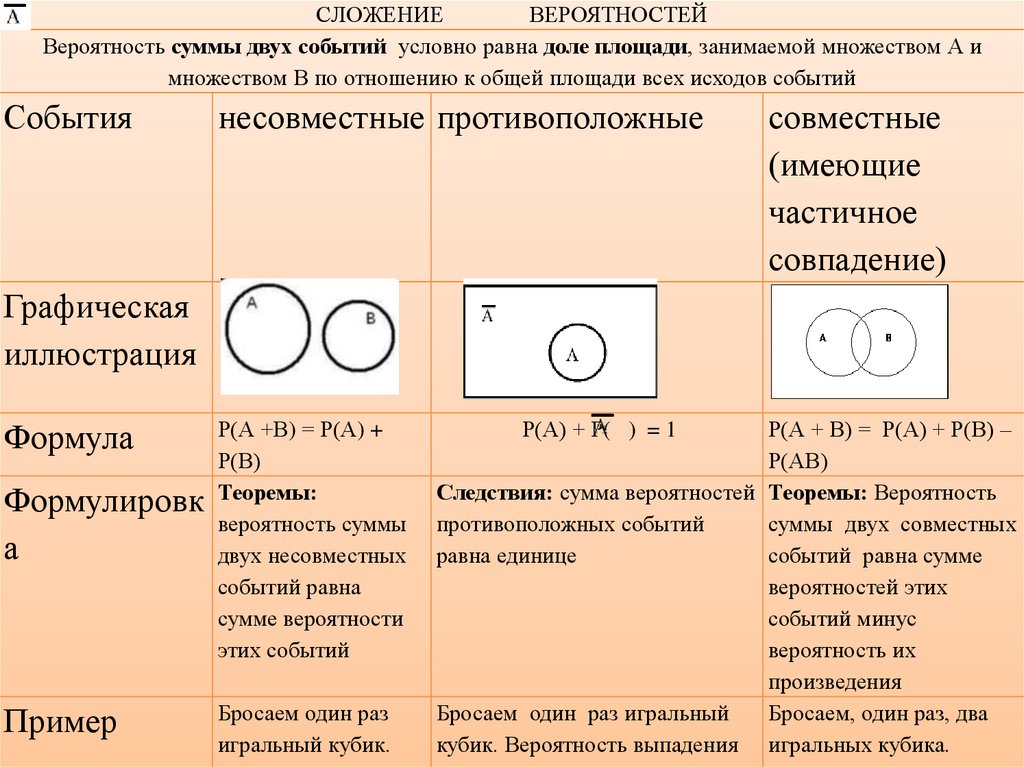
СЛОЖЕНИЕ
ВЕРОЯТНОСТЕЙ
Вероятность суммы двух событий условно равна доле площади, занимаемой множеством А и
множеством В по отношению к общей площади всех исходов событий
События
несовместные противоположные
совместные
(имеющие
частичное
совпадение)
Графическая
иллюстрация
Формула
Формулировк
а
Пример
Р(А +В) = Р(А) +
Р(В)
Теоремы:
вероятность суммы
двух несовместных
событий равна
сумме вероятности
этих событий
Бросаем один раз
игральный кубик.
Р(А) + Р( ) = 1
Р(А + В) = Р(А) + Р(В) –
Р(АВ)
Следствия: сумма вероятностей Теоремы: Вероятность
противоположных событий
суммы двух совместных
равна единице
событий равна сумме
вероятностей этих
событий минус
вероятность их
произведения
Бросаем один раз игральный
Бросаем, один раз, два
кубик. Вероятность выпадения игральных кубика.

12.

ФИЗКУЛЬТМИНУТКА

13.

Т
Е
С
Т

14.

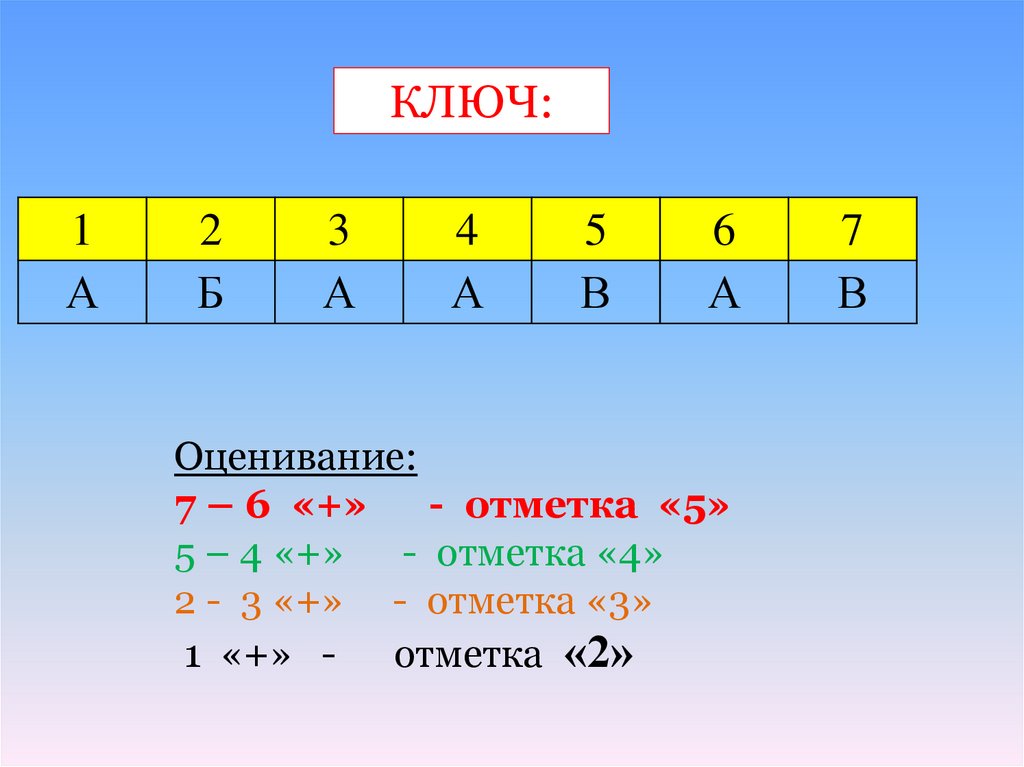
КЛЮЧ:
1
А
2
Б
3
А
4
А
5
В
6
А
Оценивание:
7 – 6 «+»
- отметка «5»
5 – 4 «+» - отметка «4»
2 - 3 «+» - отметка «3»
1 «+» - отметка «2»
7
В

15.

Ф.И
№
Утверждение
1
Сегодня я узнал…
2
На уроке я научился…
3
Мне было трудно…
4
Теперь я знаю, что…
5
Меня удивило…
6
Я бы хотел узнать, почему…
7
За урок я бы поставил себе,
потому что
Мое настроение после
занятия…
8
Ответ обучающегося

16.

Домашнее задание:
Необходимый уровень: № 523
Повышенный уровень: № 528
Творческое задание:
Придумать свою задачу на применение
изученных сегодня формул

17.

История теории вероятности
содержит очень много
неожиданных парадоксов. По
мнению Карла Пирсона, в
математике нет другого такого
раздела науки, в котором так же
легко совершить ошибку. Даже
само высказывание "вычислить
вероятность" содержит
парадокс. Ведь вероятность, в
противоположность
достоверности, есть то, чего не
знают.
подготовила:
Рогачева Наталья Владиславовна
Карл Пирсон –
английский математик,
статистик, биолог и
философ; основатель
математической
статистики, один из
основоположников
биометрики