Similar presentations:
Понятие о простых формах. Лекция 5
1.
2.
Простой формой называется совокупность граней,связанных элементами симметрии.
Грани одной простой формы должны быть
одинаковыми по своим физическим и химическим
свойствам, а в идеально развитых кристаллах — также по
своим очертаниям и величине, так как все они связаны
элементами симметрии
3.
Комбинацией называется совокупность двухили нескольких простых форм. Все ее грани
целиком не связываются элементами симметрии и,
следовательно, могут быть различными по
очертаниям, величине и по другим свойствам
4.
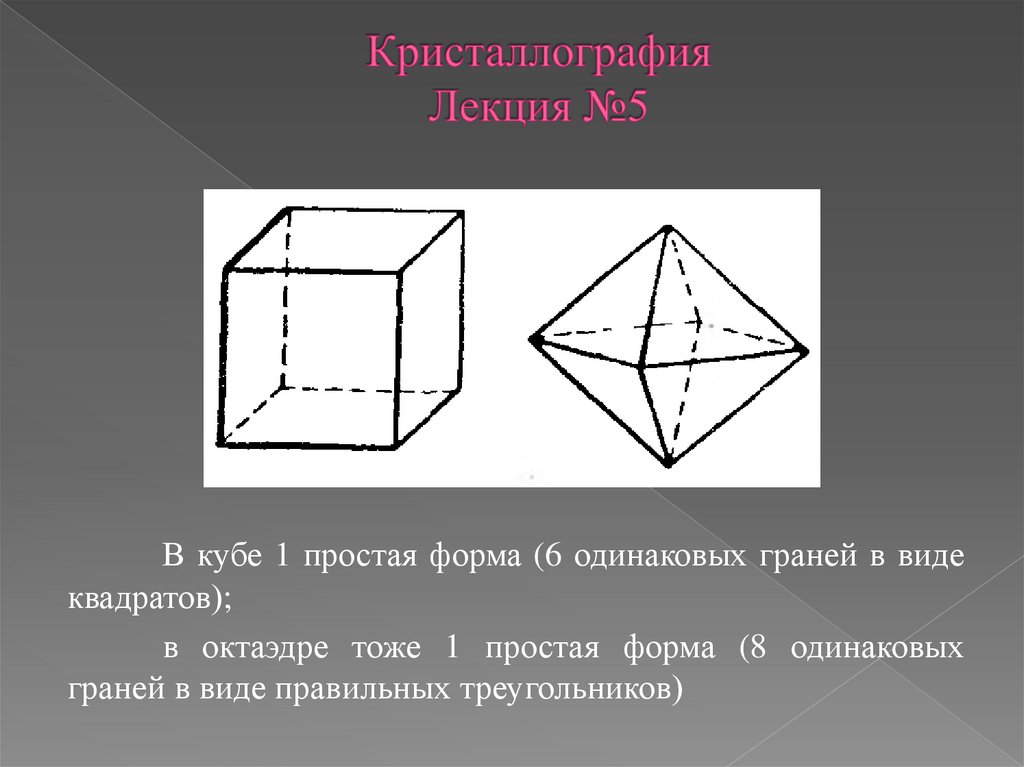
В кубе 1 простая форма (6 одинаковых граней в видеквадратов);
в октаэдре тоже 1 простая форма (8 одинаковых
граней в виде правильных треугольников)
5.
Пример кристалла, который состоит изкомбинации простых форм. В данном кристалле 2
простые формы: грани а и грани b
6.
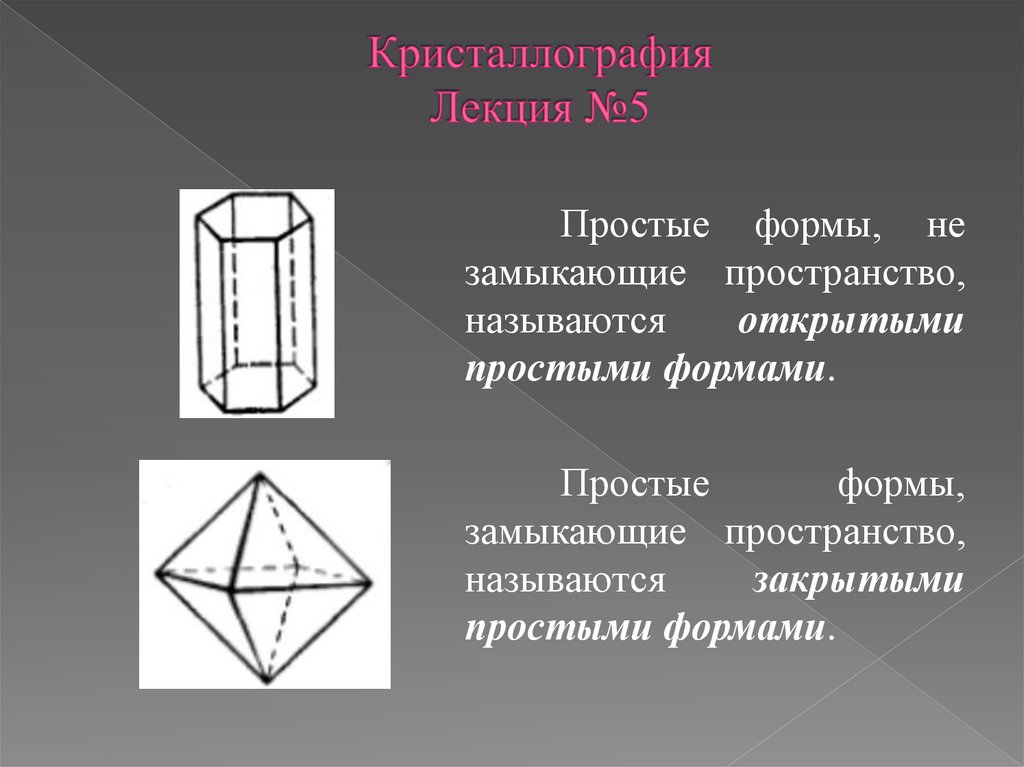
Простые формы, незамыкающие пространство,
называются
открытыми
простыми формами.
Простые
формы,
замыкающие пространство,
называются
закрытыми
простыми формами.
7.
При подсчете простых форм в комбинации (намоделях идеальных кристаллов) следует найти число
сортов граней, составляющих данный многогранник.
Различные по сорту грани всегда принадлежат
различным простым формам. Грани одного сорта в
большинстве случаев относятся к одной форме (помимо
этого, они должны быть связаны элементами
симметрии). Обычно число простых форм в
комбинации равно числу сортов граней данной фигуры
(во всяком случае не меньше его).
8.
Моно – один;ди – два;
тетра – четыре;
пента – пять;
гекса – шесть;
окта – восемь;
додека – двенадцать;
эдр – грань;
гониа – угол
9.
Тетраэдр – тетра (4) + эдр (грань) = четырехгранник;додекаэдр – додека (12) + эдр (грань) = двенадцатигранник;
пентагон – пента (5) + гон (угол) = пятиугольник;
ромбододекаэдр – ромбо (в виде ромба) + додека (12) + эдр
(грань) = двенадцатигранник, каждая грань которого в виде ромба
10.
В кристаллах кубической сингонии выделяют15 простых форм.
В основу номенклатуры
кубической сингонии положены:
простых
форм
- число граней;
- несколько форм, из которых путем их
усложнения получаются остальные
11.
К таким исходным (простейшим) формамотносятся:
1) тетраэдр (кубический) – 4 грани в виде
правильных треугольников;
2) гексаэдр – 6 граней в форме квадратов;
3) октаэдр – 8 граней в виде правильных
треугольников;
4) пентагон-додекаэдр – 12 граней в форме
пятиугольников;
5) ромбододекаэдр – 12 граней в виде ромбов.
12.
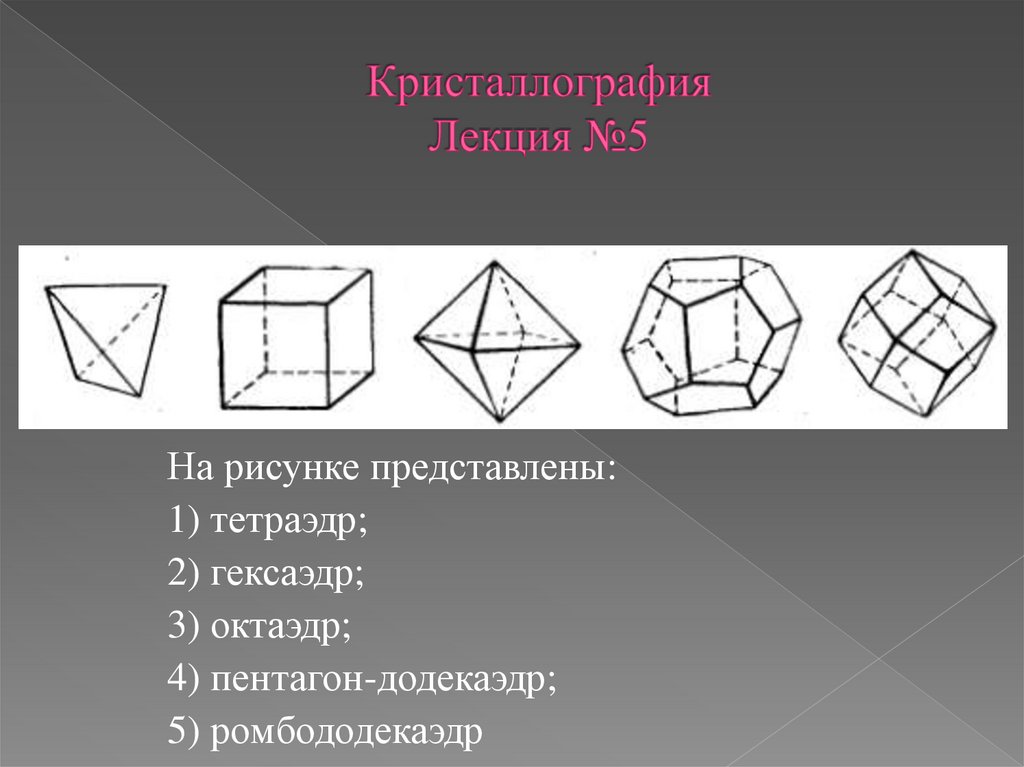
На рисунке представлены:1) тетраэдр;
2) гексаэдр;
3) октаэдр;
4) пентагон-додекаэдр;
5) ромбододекаэдр
13.
Начнем с производных тетраэдра. Утроив его грани,получим двенадцатигранник – тритетраэдр.
Полученный
многогранник
может
быть
с
треугольными (тригон-тритетраэдр), четырехугольными
(тетрагон-тритетраэдр)
и
пятиугольными
гранями
(пентагон-тритетраэдр).
14.
Тригон-тритетраэдр – тригон (треугольник) +тритетраэдр (3*4=12 граней) = 12 граней в виде
треугольников;
тетрагон-тритетраэдр
–
тетрагон
(четырехугольник) + тритетраэдр (3*4=12 граней) = 12
граней в виде четырехугольников;
пентагон-тритетраэдр – пентагон (пятиугольник)
+ тритетраэдр (3*4=12 граней) = 12 граней в виде
пятиугольников;
15.
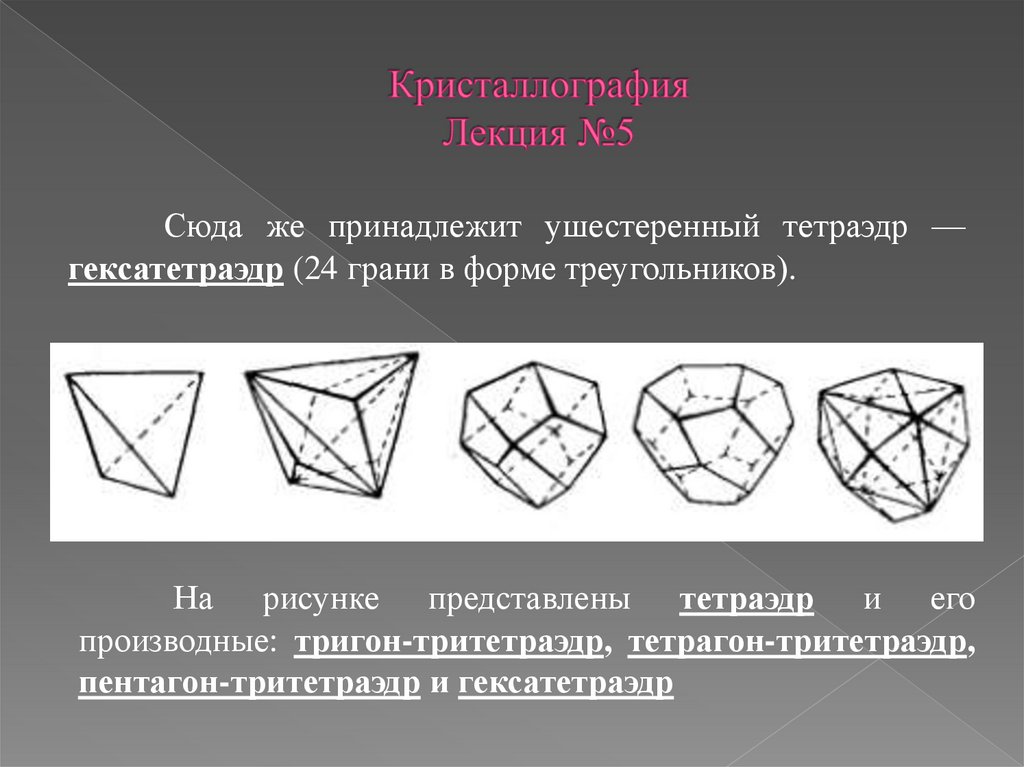
Сюда же принадлежит ушестеренный тетраэдр —гексатетраэдр (24 грани в форме треугольников).
На рисунке представлены тетраэдр и его
производные: тригон-тритетраэдр, тетрагон-тритетраэдр,
пентагон-тритетраэдр и гексатетраэдр
16.
Октаэдр дает новую серию производных, аналогичнуютетраэдрической.
Утраивая
грани
октаэдра,
получаем
три
двадцатичетырехгранника:
тригон-триоктаэдр (24 грани в виде треугольников),
тетрагон-триоктаэдр
(24
грани
в
виде
четырехугольников),
пентагон-триоктаэдр (24 грани в виде пятиугольников).
Ушестерив октаэдрические грани, приходим к
единственному сорокавосьмиграннику — гексоктаэдру (48
граней в виде треугольников).
17.
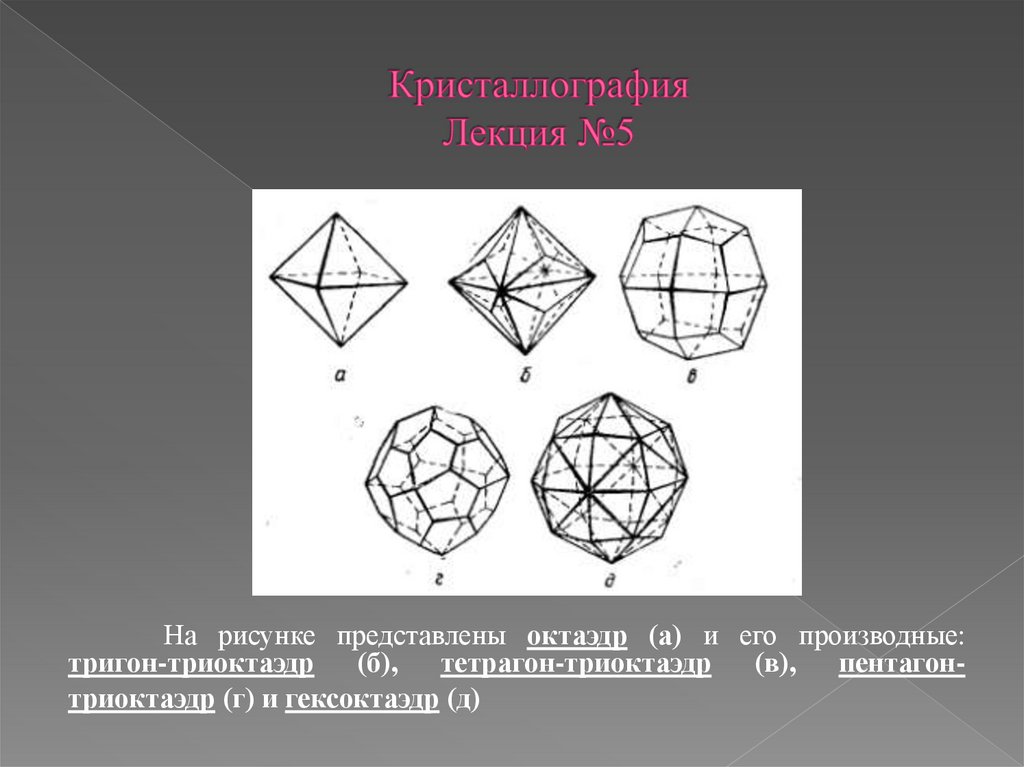
На рисунке представлены октаэдр (а) и его производные:тригон-триоктаэдр
(б), тетрагон-триоктаэдр
(в), пентагонтриоктаэдр (г) и гексоктаэдр (д)
18.
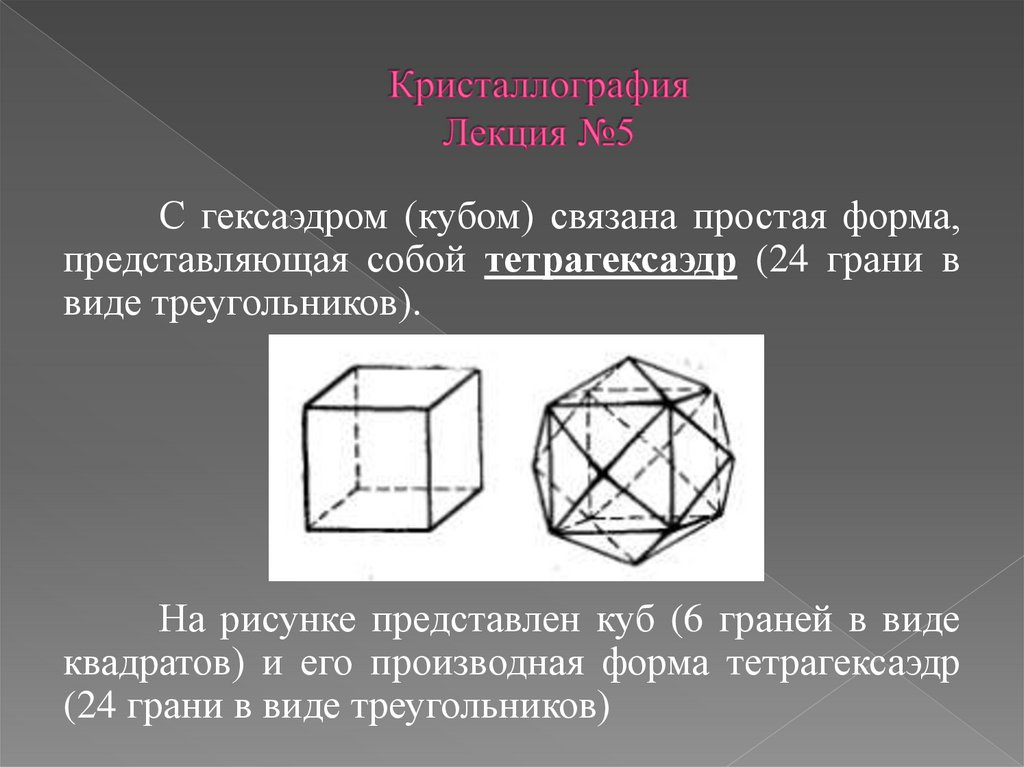
С гексаэдром (кубом) связана простая форма,представляющая собой тетрагексаэдр (24 грани в
виде треугольников).
На рисунке представлен куб (6 граней в виде
квадратов) и его производная форма тетрагексаэдр
(24 грани в виде треугольников)
19.
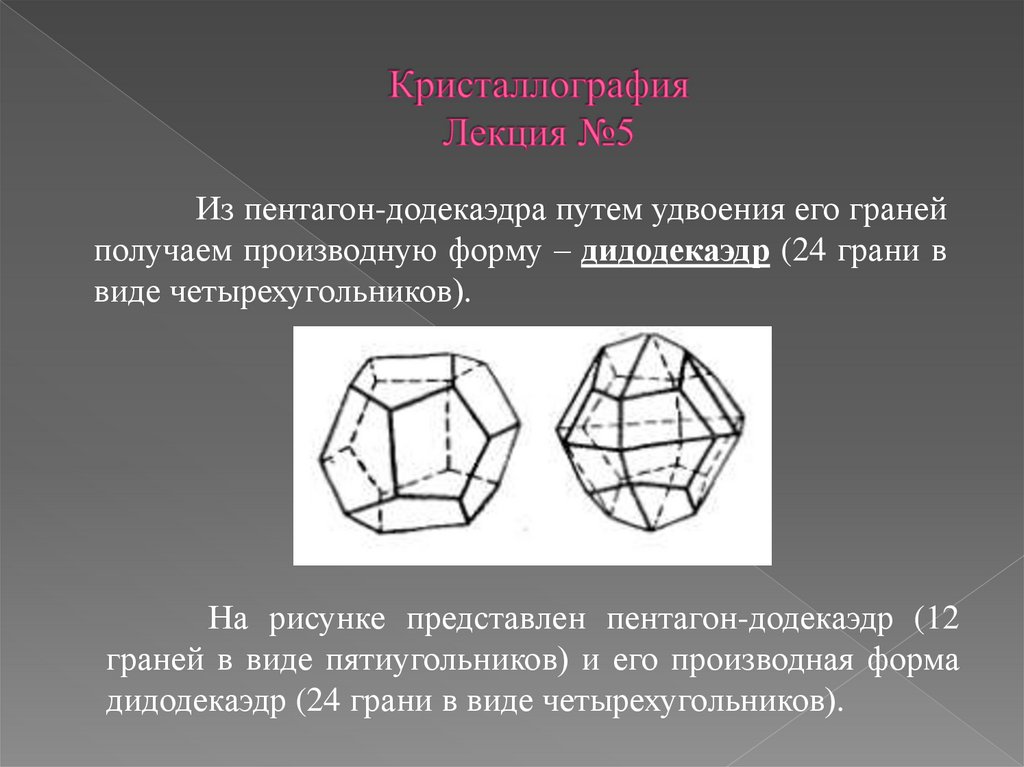
Из пентагон-додекаэдра путем удвоения его гранейполучаем производную форму – дидодекаэдр (24 грани в
виде четырехугольников).
На рисунке представлен пентагон-додекаэдр (12
граней в виде пятиугольников) и его производная форма
дидодекаэдр (24 грани в виде четырехугольников).
20.
Ромбододекаэдр (12 граней в виде ромбов)представляет собой самостоятельную простую форму,
которую нельзя получить из других простых форм. Из
ромбододекаэдра никакую простую форму вывести также
нельзя
21.
В комбинациях очертания граней простых формнередко являются искаженными за счет граней других форм.
Так, например, на рисунке изображена комбинация
гексаэдра с тетраэдром, причем квадратные грани куба,
будучи
срезанными
тетраэдрическими
плоскостями,
принимают форму шестиугольников.
22.
Три диагностических признака простых формкристаллов средней категории:
1. Расположение граней относительно главной
оси симметрии (единичного направления)
2. Взаимное расположение граней
3. Число одинаковых граней
23.
1. Расположение граней относительно главной оси симметрии(единичного направления):
- грани
направлению);
перпендикулярны
главной
оси
(единичному
- грани параллельны главной оси (единичному направлению);
- грани пересекают главную ось (единичное направление) в
одной точке;
- грани пересекают главную ось (единичное направление) в двух
точках
24.
2. Взаимное расположение граней:- нижние грани располагаются строго под
верхними;
- нижняя грань расположена симметрично
между двумя верхними;
нижняя
грань
расположена
несимметрично относительно двух верхних;
- нижняя пара граней расположена между
двумя парами верхних граней
25.
Из простых форм низших сингоний в среднююкатегорию переходят лишь формы двух типов – моноэдры и
пинакоиды.
Помимо этого, в кристаллах средней категории
встречаются 25 новых типов простых форм.
26.
Тригональная призма состоит из трех граней, параллельных L3или Li3, образуя в поперечном сечении правильный треугольник.
Дитригональная призма может рассматриваться как удвоенная
тригональная. Шесть ее граней в поперечном сечении дают
равносторонний шестиугольник с углами, повторяющимися через один.
Тетрагональная призма состоит из четырех граней,
параллельных L4 или Li4 и образует квадратное поперечное сечение.
Дитетрагональная призма отвечает удвоенной тетрагональной.
Ее восемь граней дают поперечное сечение в виде равностороннего
восьмиугольника с углами, чередующимися через один.
27.
Гексагональная призма образована шестью гранями,параллельными L6 или Li6. Поперечное сечение ее —
правильный шестиугольник.
Дигексагональная призма соответствует удвоенной
гексагональной. Ее двенадцать граней дают поперечное
сечение в виде равностороннего двенадцатиугольника с
углами, равными через один.
28.
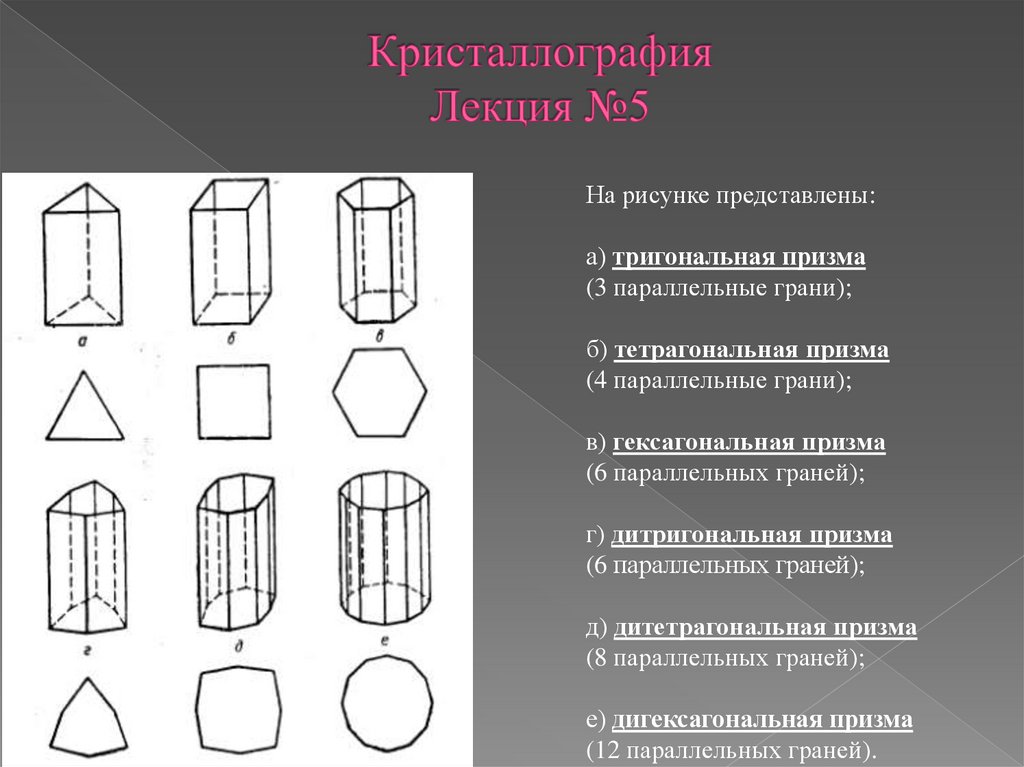
На рисунке представлены:а) тригональная призма
(3 параллельные грани);
б) тетрагональная призма
(4 параллельные грани);
в) гексагональная призма
(6 параллельных граней);
г) дитригональная призма
(6 параллельных граней);
д) дитетрагональная призма
(8 параллельных граней);
е) дигексагональная призма
(12 параллельных граней).
29.
Пирамиды пересекают всеми своими гранямиглавную ось симметрии (L3, L4, L6) в одной точке —
вершине.
Тригональная пирамида – 3 грани пересекают
ось L3 в одной точке.
Дитригональная пирамида
пересекают ось L3 в одной точке.
-
6
граней
30.
Тетрагональная пирамида – 4 грани пересекаютось L4 в одной точке.
Дитетрагональная пирамида
пересекают ось L4 в одной точке.
–
8
граней
Гексагональная
пирамида
пересекают ось L6 в одной точке.
–
6
граней
Дигексагональная пирамида
пересекают ось L6 в одной точке.
–
12
граней
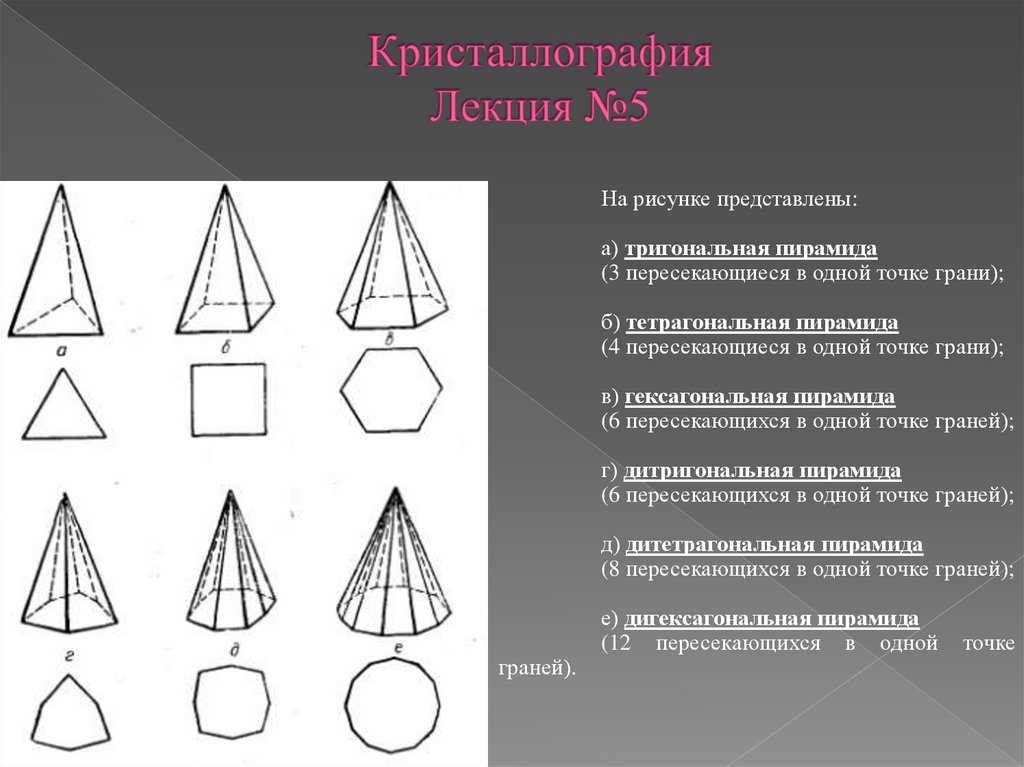
31.
На рисунке представлены:а) тригональная пирамида
(3 пересекающиеся в одной точке грани);
б) тетрагональная пирамида
(4 пересекающиеся в одной точке грани);
в) гексагональная пирамида
(6 пересекающихся в одной точке граней);
г) дитригональная пирамида
(6 пересекающихся в одной точке граней);
д) дитетрагональная пирамида
(8 пересекающихся в одной точке граней);
граней).
е) дигексагональная пирамида
(12 пересекающихся в одной
точке
32.
Наконец, такой же ряд имеем и для дипирамид. Грани их пересекают главнуюось симметрии L3, L4, Li4, L6 и Li6 в двух точках, причем нижние грани располагаются
точно под верхними.
Тригональная дипирамида – 6 граней пересекают ось L3 в двух точках.
Дитригональная дипирамида – 12 граней пересекают ось L3 в двух точках.
Тетрагональная дипирамида – 8 граней пересекают ось L4 в двух точках.
Дитетрагональная дипирамида – 16 граней пересекают ось L4 в двух точках.
Гексагональная дипирамида – 12 граней пересекают ось L6 в двух точках.
Дигексагональная дипирамида – 24 грани пересекаю ось L6 в двух точках.
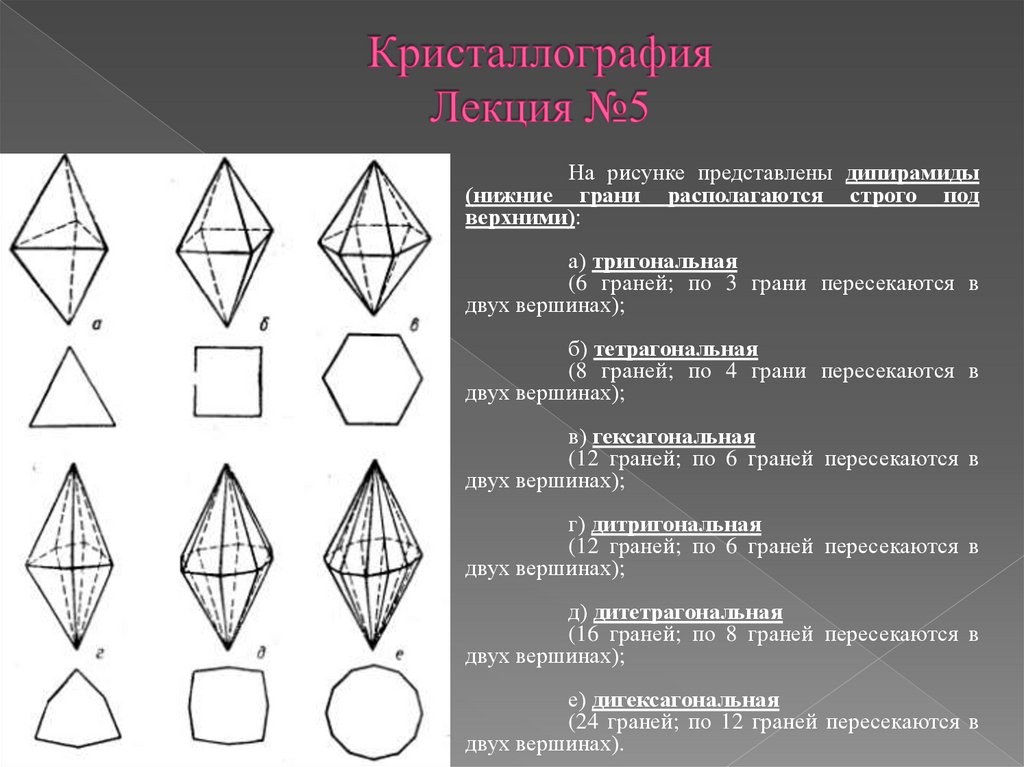
33.
На рисунке представлены дипирамиды(нижние грани располагаются строго под
верхними):
а) тригональная
(6 граней; по 3 грани пересекаются в
двух вершинах);
б) тетрагональная
(8 граней; по 4 грани пересекаются в
двух вершинах);
в) гексагональная
(12 граней; по 6 граней пересекаются в
двух вершинах);
г) дитригональная
(12 граней; по 6 граней пересекаются в
двух вершинах);
д) дитетрагональная
(16 граней; по 8 граней пересекаются в
двух вершинах);
е) дигексагональная
(24 граней; по 12 граней пересекаются в
двух вершинах).
34.
Особняком стоят тетрагональный тетраэдр,ромбоэдр и серии скаленоэдров и трапецоэдров.
Тетрагональный тетраэдр – 4 грани в виде
равнобедренных треугольников. Нижняя грань его
расположена симметрично между двумя верхними и
(наоборот). Главную ось пересекает в двух точках.
Ромбоэдр – 6 граней в виде ромбов. Нижняя грань
относительно
верхних
двух
располагается
симметрично. Главную ось пересекает в двух точках.
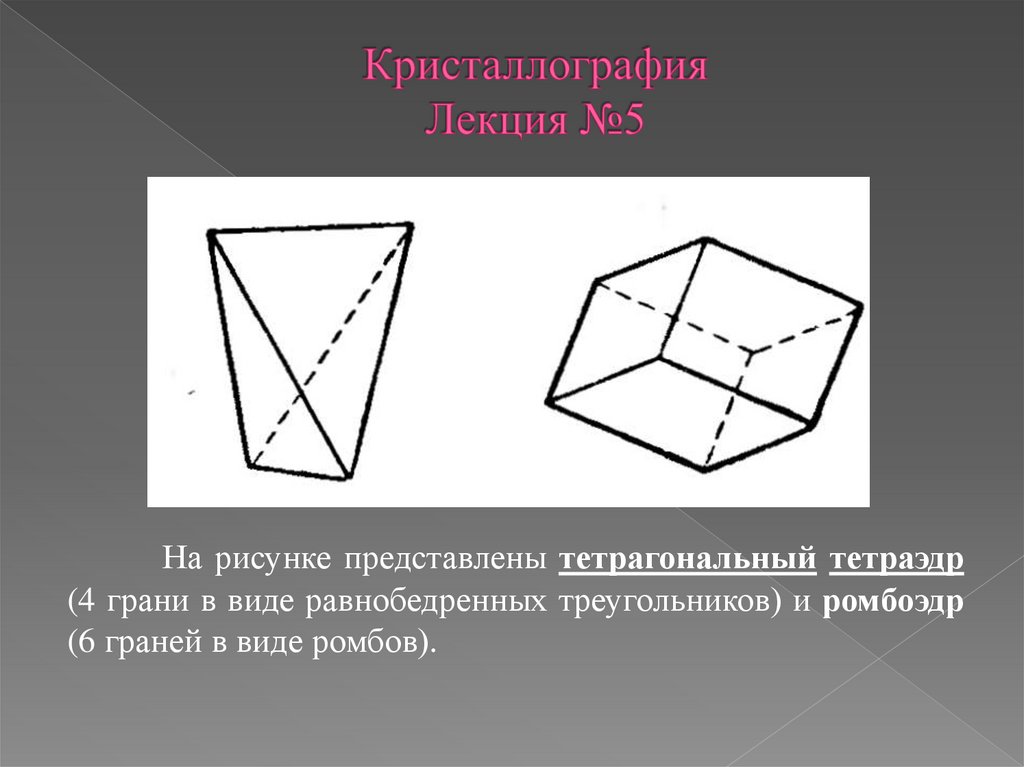
35.
На рисунке представлены тетрагональный тетраэдр(4 грани в виде равнобедренных треугольников) и ромбоэдр
(6 граней в виде ромбов).
36.
Кследующей
серии
принадлежат
тетрагональный и тригональный скаленоэдры.
Грани их пересекают главную ось в двух точках. Пара
нижних граней располагается симметрично между
двумя парами верхних. Очертания граней отвечают
разносторонним треугольникам.
Тетрагональный скаленоэдр – 8 граней в виде
разносторонних треугольников.
Тригональный скаленоэдр – 12 граней в виде
разносторонних треугольников.
37.
Нарисунке
изображены
тетрагональный
скаленоэдр (8 граней в виде разносторонних
треугольников) и тригональный скаленоэдр (12 граней в
виде разносторонних граней).
38.
Трапецоэдрическиеграни
представляют
собой
четырехугольники с одной парой равных соседних сторон. В
трапецоэдрах присутствуют лишь оси симметрии (Р и С не
встречаются), поэтому у них нижняя грань располагается
несимметрично относительно двух верхних граней.
Тригональный
четырехугольников;
трапецоэдр
—
6
граней
в
виде
тетрагональный
четырехугольников;
трапецоэдр
—
8
граней
в
виде
гексагональный трапецоэдр — 12 граней в виде
четырехугольников.
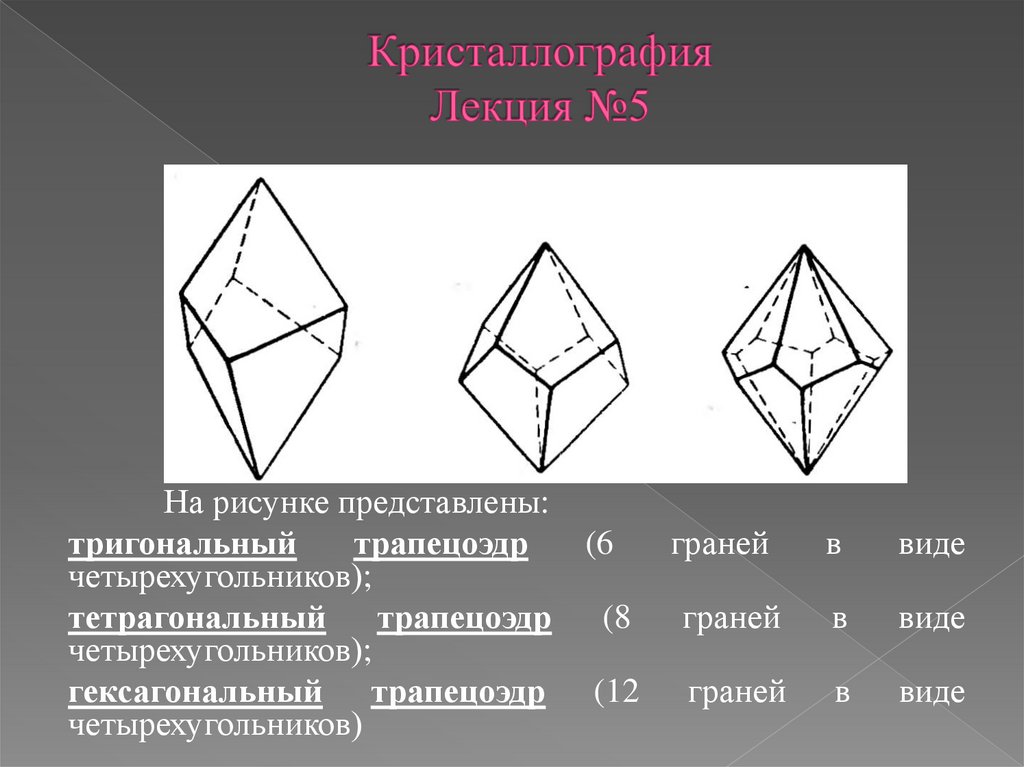
39.
На рисунке представлены:тригональный
трапецоэдр
(6
граней
четырехугольников);
тетрагональный трапецоэдр (8 граней
четырехугольников);
гексагональный трапецоэдр (12 граней
четырехугольников)
в
виде
в
виде
в
виде
40.
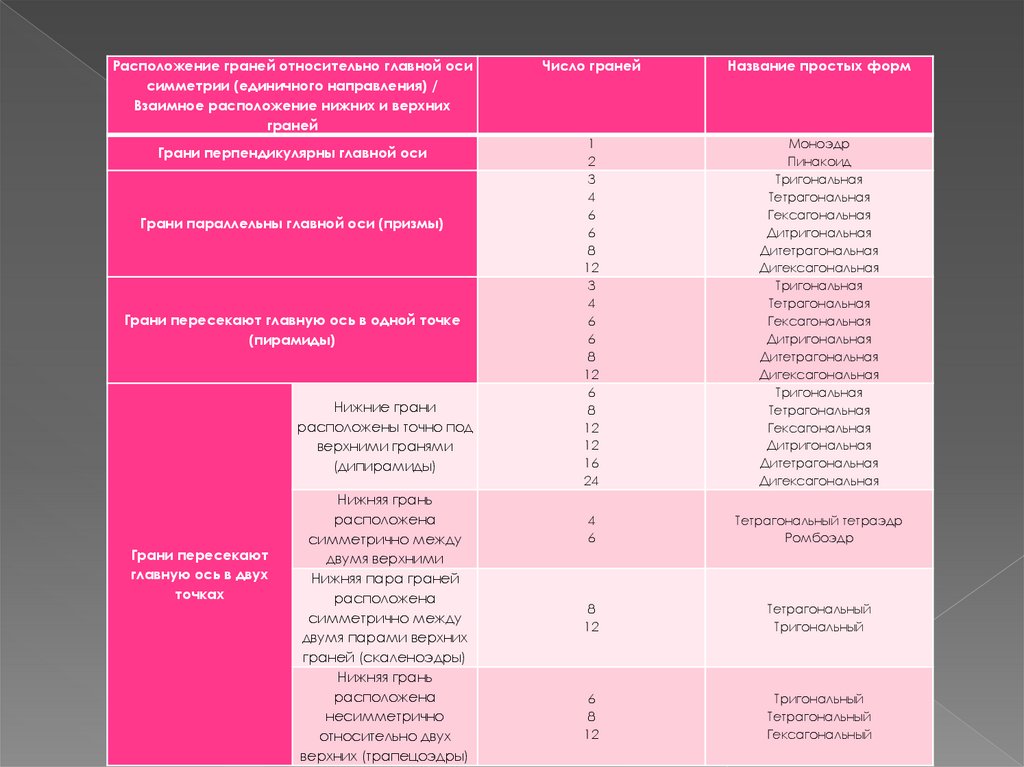
Расположение граней относительно главной осисимметрии (единичного направления) /
Взаимное расположение нижних и верхних
граней
Грани перпендикулярны главной оси
Грани параллельны главной оси (призмы)
Грани пересекают главную ось в одной точке
(пирамиды)
Нижние грани
расположены точно под
верхними гранями
(дипирамиды)
Грани пересекают
главную ось в двух
точках
Нижняя грань
расположена
симметрично между
двумя верхними
Нижняя пара граней
расположена
симметрично между
двумя парами верхних
граней (скаленоэдры)
Нижняя грань
расположена
несимметрично
относительно двух
верхних (трапецоэдры)
Число граней
Название простых форм
1
2
3
4
6
6
8
12
3
4
6
6
8
12
6
8
12
12
16
24
Моноэдр
Пинакоид
Тригональная
Тетрагональная
Гексагональная
Дитригональная
Дитетрагональная
Дигексагональная
Тригональная
Тетрагональная
Гексагональная
Дитригональная
Дитетрагональная
Дигексагональная
Тригональная
Тетрагональная
Гексагональная
Дитригональная
Дитетрагональная
Дигексагональная
4
6
Тетрагональный тетраэдр
Ромбоэдр
8
12
Тетрагональный
Тригональный
6
8
12
Тригональный
Тетрагональный
Гексагональный
41.
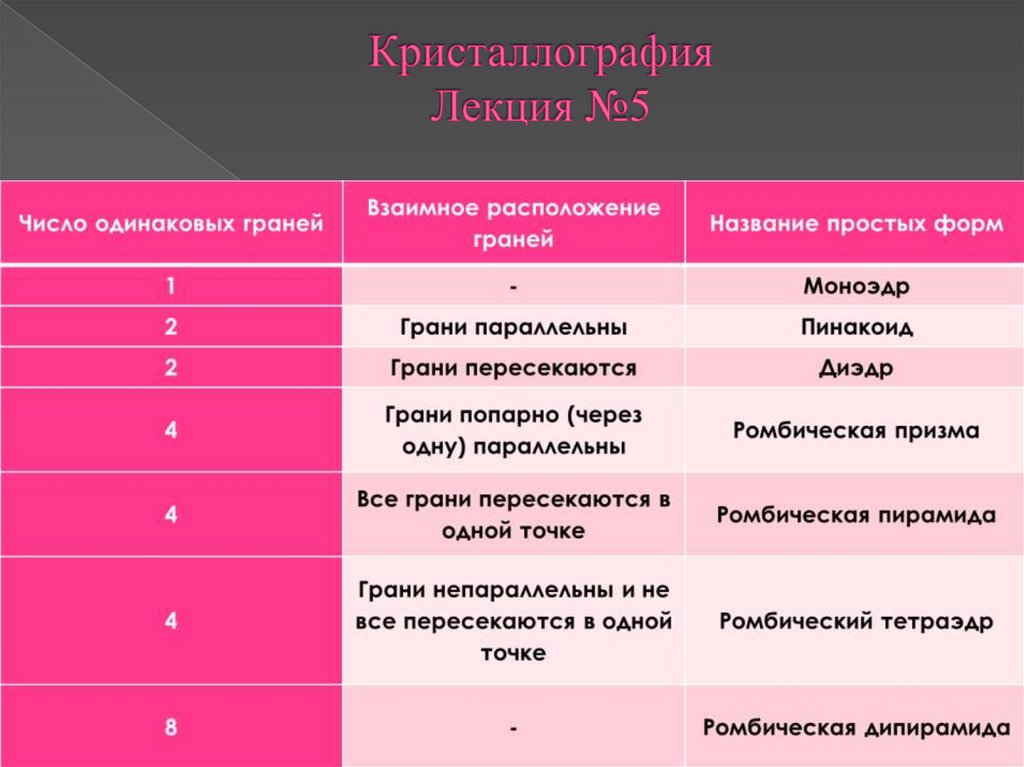
В кристаллах низшей категории возможны 7 типов простых форм:а) моноэдр;
б) пинакоид;
в) диэдр;
г) ромбическая призма;
д) ромбический тетраэдр;
е) ромбическая пирамида
ж) ромбическая дипирамида
42.
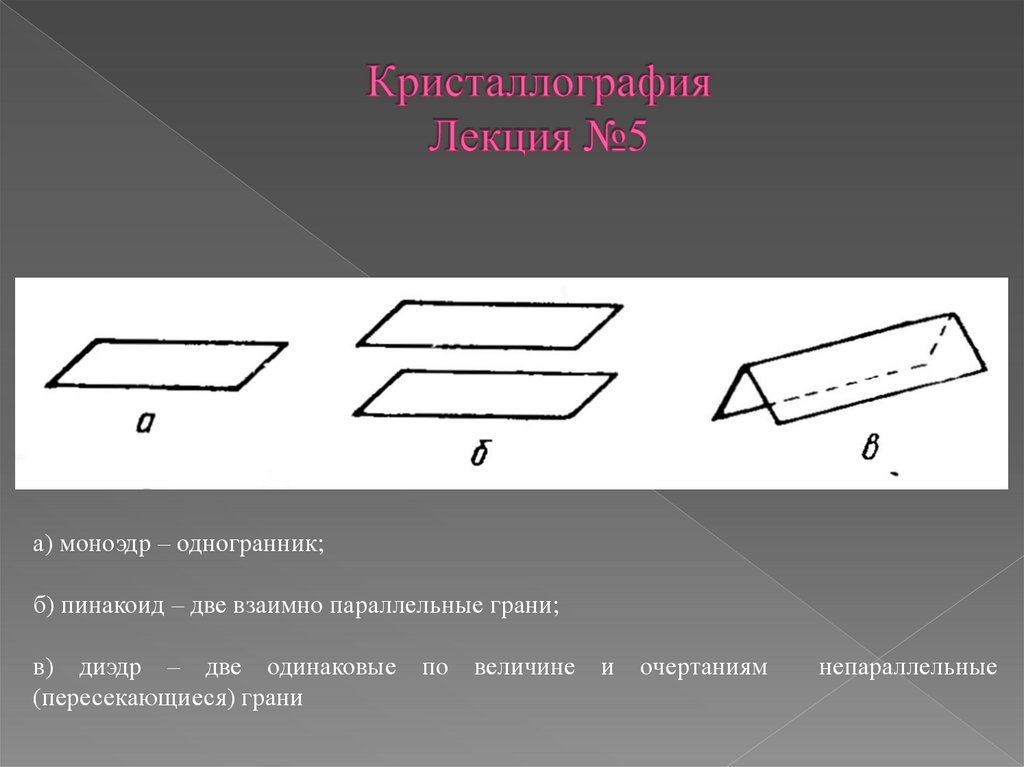
а) моноэдр – одногранник;б) пинакоид – две взаимно параллельные грани;
в) диэдр – две одинаковые по величине и очертаниям
(пересекающиеся) грани
непараллельные
43.
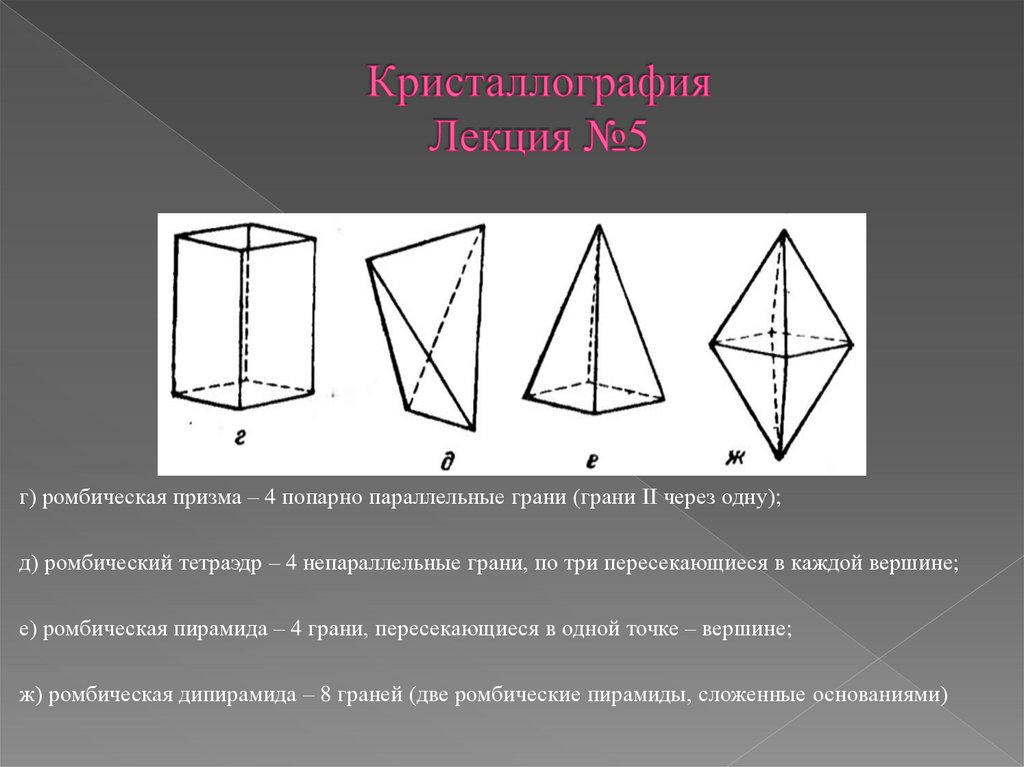
г) ромбическая призма – 4 попарно параллельные грани (грани II через одну);д) ромбический тетраэдр – 4 непараллельные грани, по три пересекающиеся в каждой вершине;
е) ромбическая пирамида – 4 грани, пересекающиеся в одной точке – вершине;
ж) ромбическая дипирамида – 8 граней (две ромбические пирамиды, сложенные основаниями)




























 chemistry
chemistry








