Similar presentations:
Квадратичная функция
1.
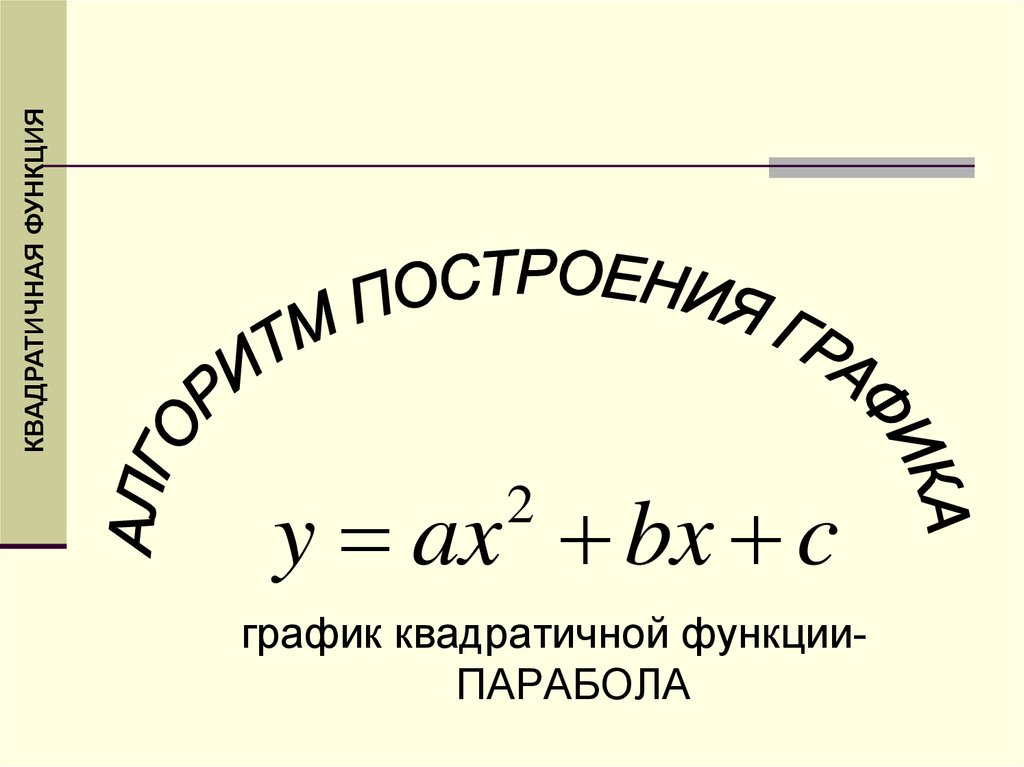
КВАДРАТИЧНАЯ ФУНКЦИЯy ax bx c
2
график квадратичной функцииПАРАБОЛА
2.
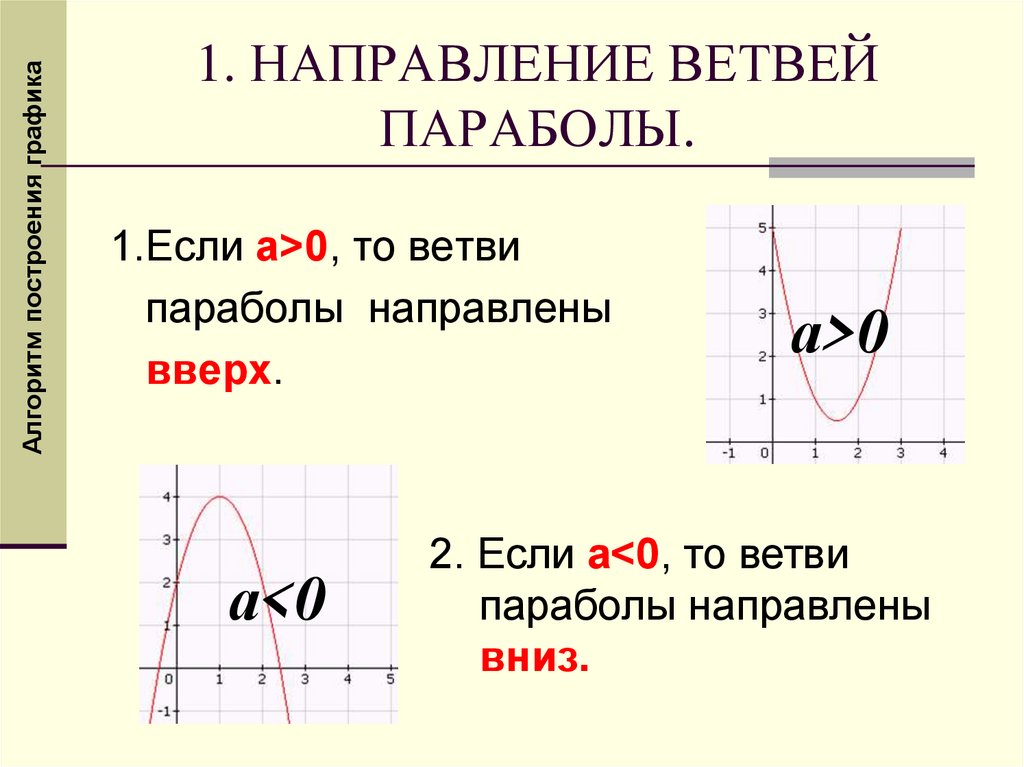
Алгоритм построения графика1. НАПРАВЛЕНИЕ ВЕТВЕЙ
ПАРАБОЛЫ.
1.Если а>0, то ветви
параболы направлены
вверх.
а<0
а>0
2. Если а<0, то ветви
параболы направлены
вниз.
3.
Алгоритм построения графикаНапример:
y 3x 2 x 4
2
2 2
y x 4
3
a=3,
a>0 , то ветви параболы
направлены вверх
2
a= ,
3
a<0 , то ветви параболы
направлены вниз
4.
Алгоритм построения графикаНапример:
y 3x 4 x
2
x
y
2
2
a=-4,
a<0 , то ветви параболы
направлены вниз
1
a= 2 ,
a>0 , то ветви параболы
направлены вверх
5.
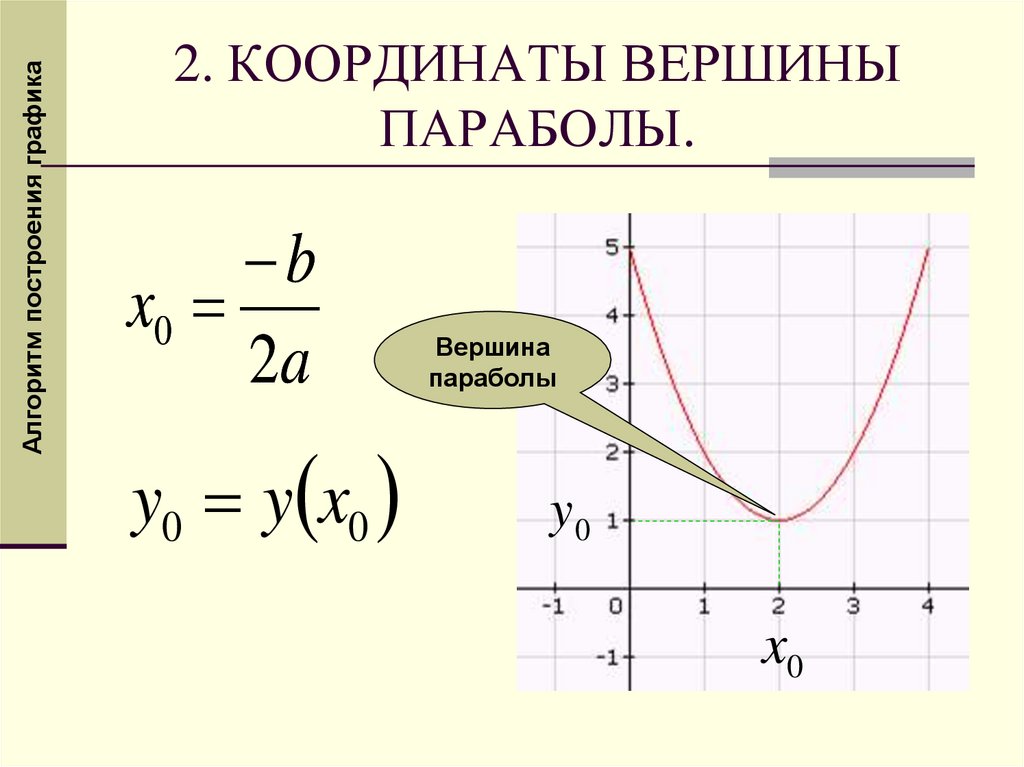
Алгоритм построения графика2. КООРДИНАТЫ ВЕРШИНЫ
ПАРАБОЛЫ.
b
x0
2a
y0 y x0
Вершина
параболы
y0
x0
6.
Алгоритм построения графикаПример №1
b
x0
2a
y x 4x 5
y0 y x0
2
a=1, b=-4.
4
x0 2
2
y0 y 2 2 4 2 5 1
2
(2; 1) координаты вершины параболы
7.
Алгоритм построения графикаb
x0
2a
Пример №2
y 2x 4
2
a=2, b=0.
0
x0 0
4
y0 y x0
y0 y 0 2 0 4 4
2
(0;4) координаты вершины параболы
8.
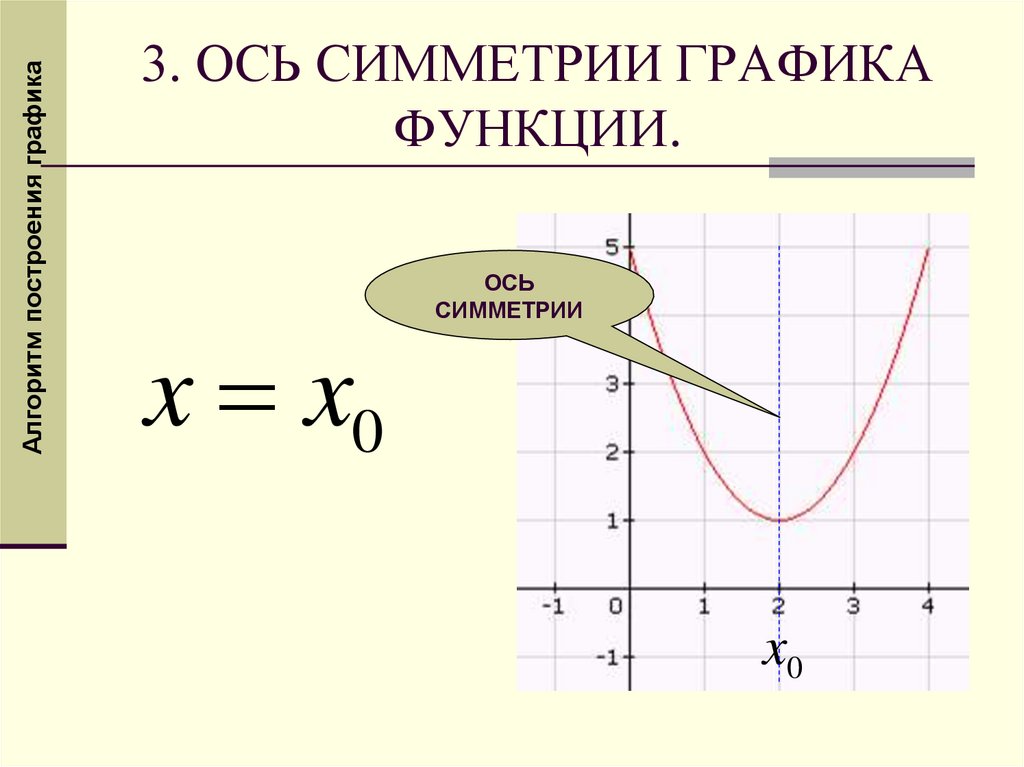
Алгоритм построения графика3. ОСЬ СИММЕТРИИ ГРАФИКА
ФУНКЦИИ.
x x0
ОСЬ
СИММЕТРИИ
x0
9.
Алгоритм построения графикаНапример:
y x 4x 5
2
Координаты вершины параболы (2;1), т.е.
x0=2 значит ось симметрии параболы – прямая x=2
y 2x 4
2
Координаты вершины параболы (0;-4), т.е.
x0=0 значит ось симметрии параболы – прямая x=0
(совпадает с осью ОY)
10.
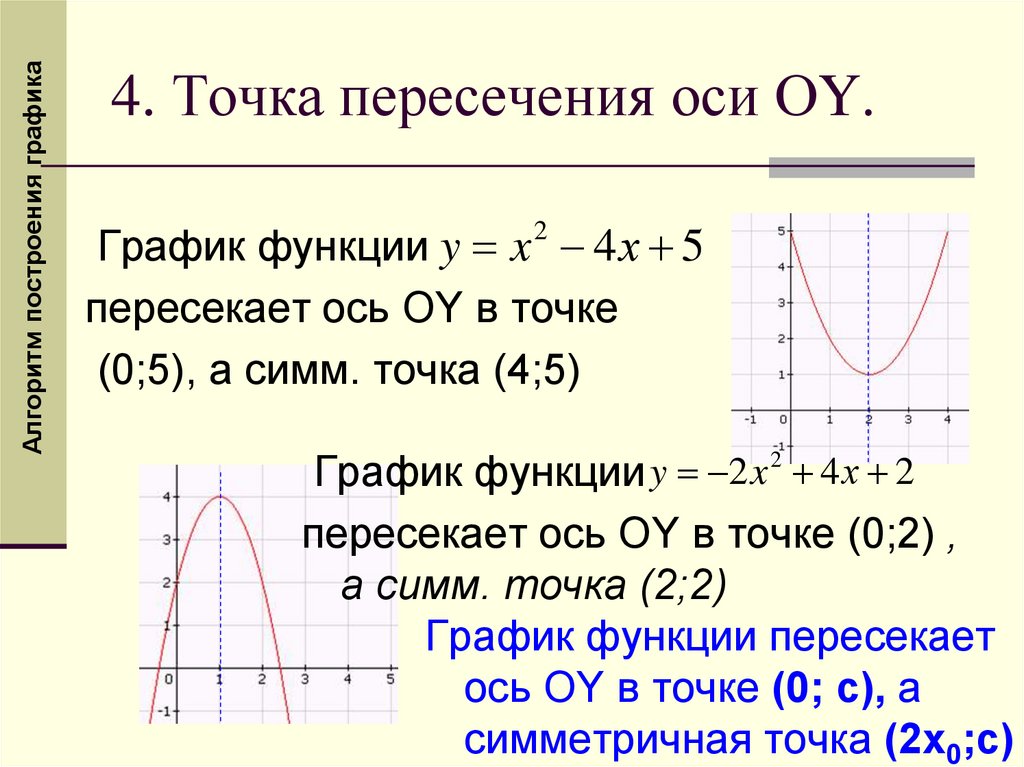
Алгоритм построения графика4. Точка пересечения оси ОY.
График функции y x 2 4 х 5
пересекает ось OY в точке
(0;5), а симм. точка (4;5)
График функции y 2 x 2 4 х 2
пересекает ось OY в точке (0;2) ,
а симм. точка (2;2)
График функции пересекает
ось OY в точке (0; с), а
симметричная точка (2х0;с)
11.
Алгоритм построения графика5. Нули функции
y x 4х 5
2
y 2 x 2 4 х 2
12.
Алгоритм построения графика6. Дополнительные точки.
Составляем таблицу для значений х, взятых по
одну сторону от оси симметрии.
Например: у(х)=х2-4х+5 , т.к. ось симметрии х=2 ,
то берем значения х>2 или х<2.
x 1
х 3
у (1) 12 4 1 5 2
у (3) 32 4 3 5 2
х
1 3
y(x)
2 2
13.
ПримерПостроение графика квадратичной
функции.
у х 2x 4
2
14.
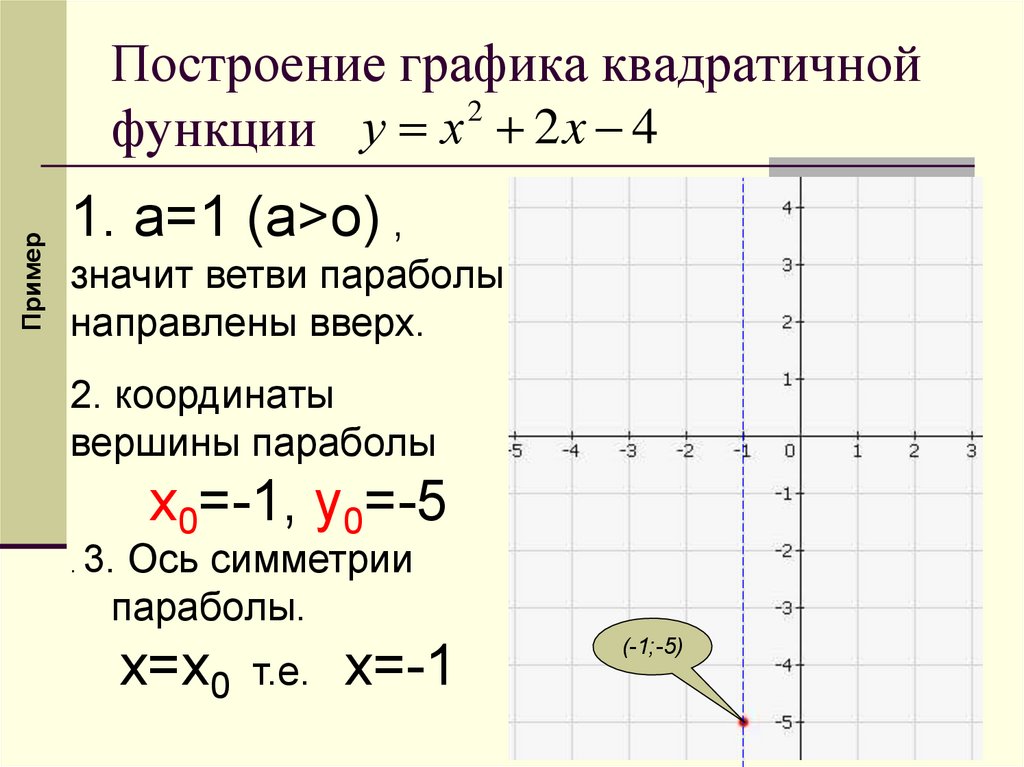
ПримерПостроение графика квадратичной
2
функции у х 2 x 4
1. а=1 (а>o) ,
значит ветви параболы
направлены вверх.
2. координаты
вершины параболы
х0=-1, у0=-5
.
3. Ось симметрии
параболы.
х=х0 т.е. х=-1
(-1;-5)
15.
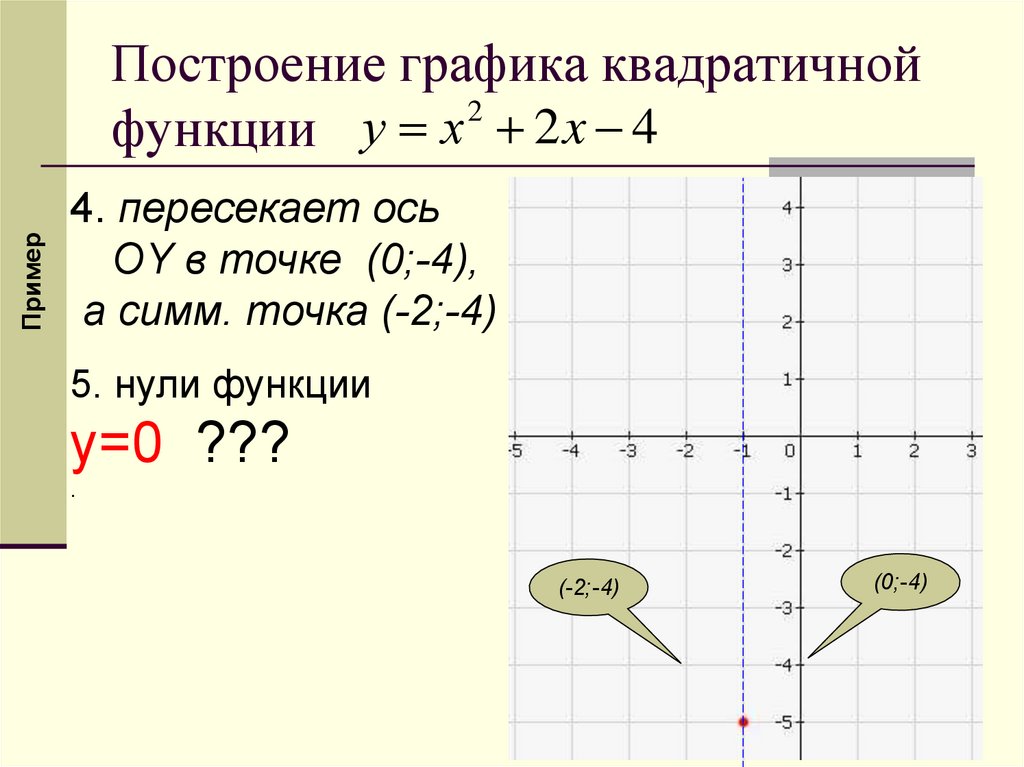
ПримерПостроение графика квадратичной
2
функции у х 2 x 4
4. пересекает ось
OY в точке (0;-4),
а симм. точка (-2;-4)
5. нули функции
у=0 ???
.
(-2;-4)
(0;-4)
16.
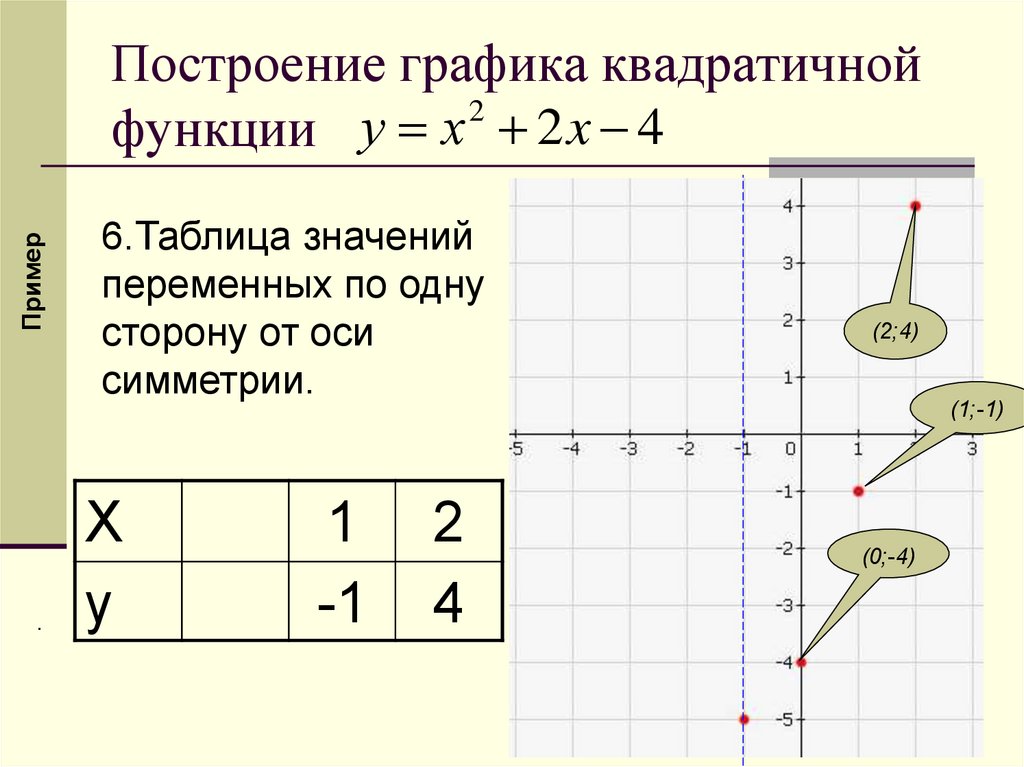
ПримерПостроение графика квадратичной
2
функции у х 2 x 4
.
6.Таблица значений
переменных по одну
сторону от оси
симметрии.
Х
у
1
-1
2
4
(2;4)
(1;-1)
(0;-4)
17.
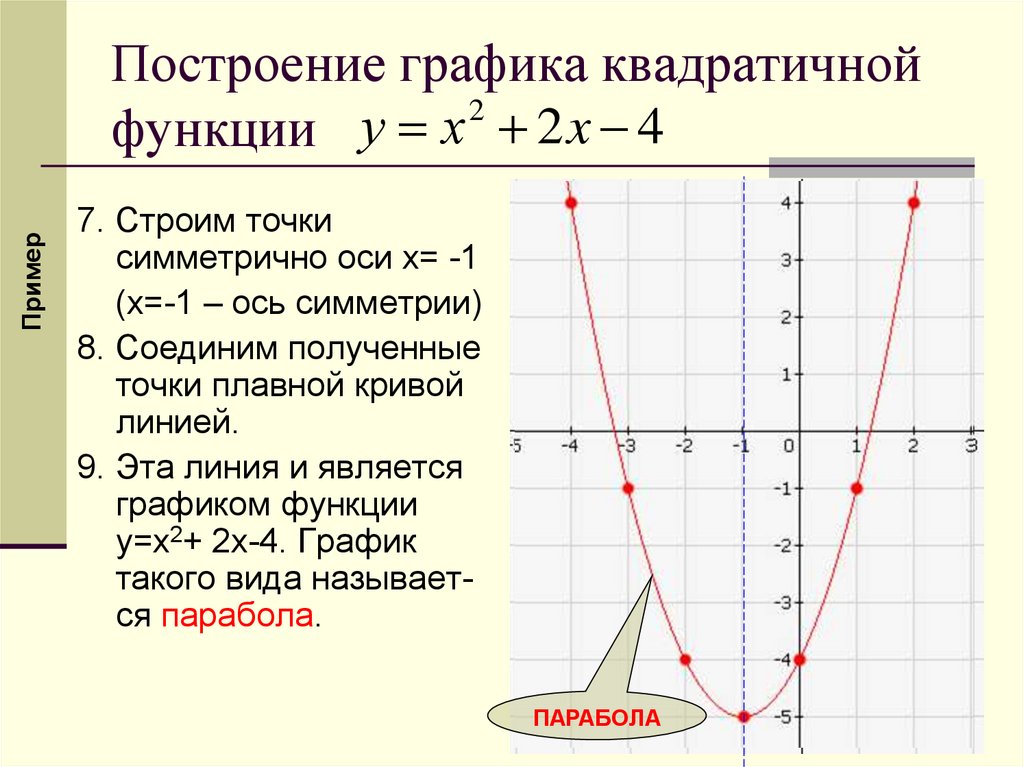
ПримерПостроение графика квадратичной
2
функции у х 2 x 4
7. Строим точки
симметрично оси x= -1
(x=-1 – ось симметрии)
8. Соединим полученные
точки плавной кривой
линией.
9. Эта линия и является
графиком функции
y=x2+ 2x-4. График
такого вида называется парабола.
ПАРАБОЛА
18.
КВАДРАТИЧНАЯ ФУНКЦИЯy ax bx c
2
график квадратичной функции- ПАРАБОЛА
1. Направление ветвей параболы.
2. Координаты вершины параболы.
3. Ось симметрии графика функции.
4. Точка пересечения оси ОY.
5. Нули функции
6. Дополнительные точки.
19.
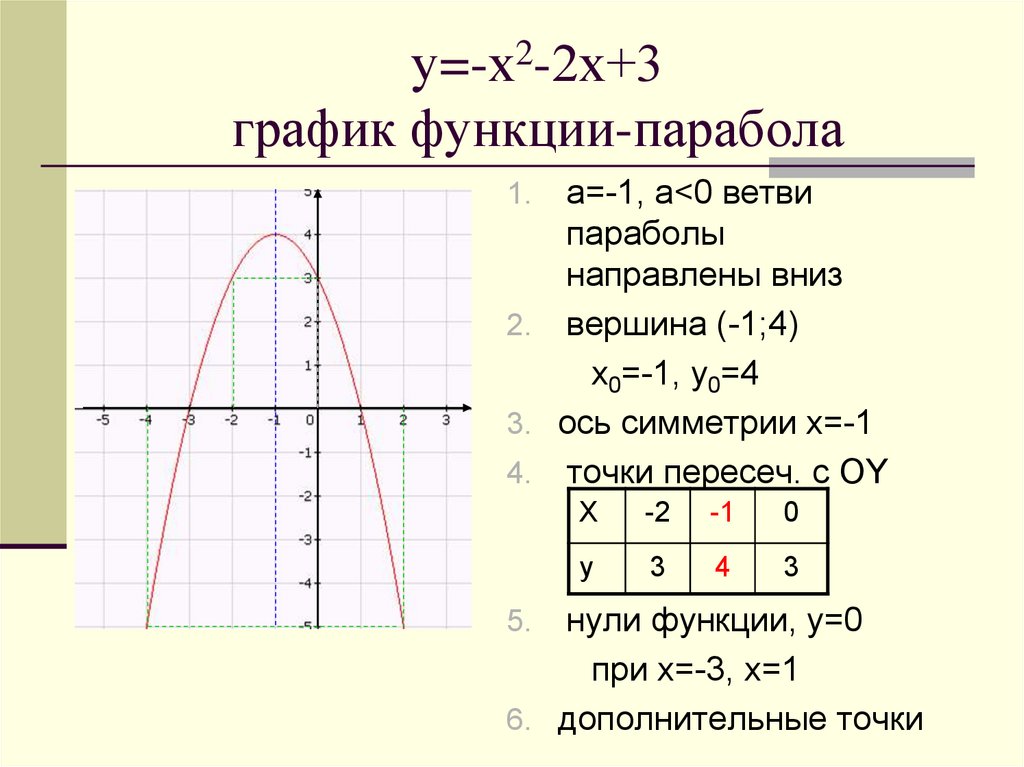
у=-х2-2х+3график функции-парабола
а=-1, a<0 ветви
параболы
направлены вниз
2. вершина (-1;4)
х0=-1, у0=4
3. ось симметрии х=-1
4. точки пересеч. с OY
1.
Х
-2
-1
0
у
3
4
3
нули функции, у=0
при х=-3, х=1
6. дополнительные точки
5.








 mathematics
mathematics








