Similar presentations:
Контроль передачи данных CRC
1.
ДисциплинаМАТЕМАТИЧЕСКИЕ МОДЕЛИ БЕЗОПАСНОСТИ
ИНФОРМАЦИОННЫХ СИСТЕМ
КОНТРОЛЬ ПЕРЕДАЧИ ДАННЫХ
CRC
2.
Цифровая система связи** Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. – М.: Мир, 1986. – 576 с.
2
3.
Кодирование, контролирующее ошибкиКлод Шеннон показал, что с каждый канал характеризуется измеряемым в битах числом С, называемым
пропускной способностью канала связи (1948г.)
Если требуемая от системы связи скорость передачи информации R, измеряемая в битах в секунду,
меньше C, то, используя коды, контролирующие ошибки, для данного канала можно построить такую
систему связи, что вероятность ошибки на выходе будет сколь угодно мала.
3
4.
Кодирование, контролирующее ошибкиСуществует два основных класса кодов: блоковые коды и древовидные коды.
Блоковый код задает блок из k информационных символов n-символьным кодовым словом.
Скорость R блокового кода равна R = k/n.
Древовидный код отображает бесконечную последовательность информационных символов,
поступающую со скоростью k0 символов за один интервал времени, в непрерывную
последовательность символов кодового слова со скоростью n0.
Линейные блоковые коды (1950г., Ричард Хэмминг).
Циклические коды на базе полей Галуа.
Коды Боуза – Чоудхури – Хоквингема (БЧХ, 1960г.)
Коды, основанные на спектральных методах. Преобразование Фурье в поле Галуа.
Многомерные спектральные методы.
Сверточные коды.
Вероятностные подходы.
Мажоритарные подходы.
4
5.
Пример простейшего кодаПроверка на четность
0000
0001
0010
0011
<->
<->
<->
<->
00000
00011
00101
00110
Сообщение
Бит контрольной суммы
Представляет собой высокоскоростной (5, 4) – код, который может обнаружить ошибки, не может их
исправить.
5
6.
Контрольная сумма сложениемМетоды обнаружения ошибок предназначены для выявления повреждений сообщений при их
передаче по зашумленным каналам (вносящих эти ошибки). Для этого передающее устройство создает
некоторое число, называемое контрольной суммой и являющееся функцией сообщения, и добавляет его
к этому сообщению.
Приемное устройство, используя тот же самый алгоритм, рассчитывает контрольную сумму принятого
сообщения и сравнивает ее с переданным значением.
Например:
Сообщение:
Сообщение с контрольной суммой:
Сообщение после передачи:
6
6
6
23
23
27
4
4 33
4 33
Подходы к формированию надежной контрольной суммы:
1. Ширина: Размер регистра для вычислений должен обеспечивать изначальную низкую
вероятность ошибки.
2. Случайность: Необходим такой алгоритм расчета, когда каждый новый байт может оказать
влияние на любые биты регистра.
6
7.
Циклический избыточный кодCRC: Cyclic Redundancy Code или Cyclic Redundancy Check
Циклические коды просты в реализации и подходят для обнаружения пакетных ошибок:
непрерывных последовательностей ошибочных символов данных в сообщениях. Это важно, потому что
пакетные ошибки являются распространенными ошибками передачи во многих каналах связи, включая
магнитные и оптические запоминающие устройства.
n-разрядный CRC, применяемый к блоку данных произвольной длины, и при расположении
контрольной суммы непосредственно вслед за данными, обнаруживает любой одиночный пакет ошибок
длиной не более n бит.
Коды БЧХ —широкий класс циклических кодов, применяемых для защиты информации от ошибок.
Отличается возможностью построения кода с заранее определёнными корректирующими свойствами, а
именно, минимальным кодовым расстоянием. Частным случаем БЧХ-кодов является код Рида—Соломона.
Коды Рида—Соломона (Reed–Solomon codes) — недвоичные циклические коды, позволяющие
исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов
(блоки), например байты.
Код Рида—Соломона является частным случаем БЧХ-кода.
7
8.
Расстояние ХэммингаРасстояние Хэмминга (кодовое расстояние) — число позиций, в которых соответствующие
символы двух слов одинаковой длины различны. Расстояние Хэмминга применяется для строк
одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей
расстояние в метрическом пространстве) объектов одинаковой размерности.
Расстояние Хэмминга:
Расстояние Хэмминга — частный случай метрики Минковского:
8
9.
Хеш-функцииCRC является Хеш-функцией — функцией, осуществляющей по определенному алгоритму
преобразование массива входных данных произвольной длины в выходную битовую строку
установленной длины. Преобразование, производимое хеш-функцией, называется сверткой,
хешированием. Исходные данные называются входным массивом, «ключом» или «сообщением».
Результат преобразования называется «хешем», «хеш-кодом», «хеш-суммой» или «сводкой».
Примеры:
1. Контрольная сумма — число фиксированной длины. Например, если для ключа длиной в 56 бит
используется контрольная сумма ключа размером 8 бит, то эти 8 бит можно рассматривать как хешкод от предыдущих 56.
2. Cyclic redundancy check — самые разные длины. Обычно от 1-го бита до 64-х бит.
3. Алгоритм Пирсона для строк — популярный алгоритм для вычисления хеш-суммы от строки методом
подстановки.
4. Деление на простое число. Если вычислять хеш-код по модулю не простых чисел, то будет
получаться много коллизий (хеш-код от них одинаковый).
9
10.
Требования к стойкости Хеш-функций1. Сложность к вычислению прообраза: если известно значение функции, тогда должно быть сложно
найти такое сообщение, хеш-функция от которого равна известному.
2. Стойкость вычисления второго прообраза: пусть есть одно значение, и известен хеш-код этого
значения. Тогда злоумышленнику должно быть сложно найти еще одно такое значение, чтобы его
хеш-функция совпадала с хеш-функцией первого значения.
3. Сложность к поиску коллизий: должно быть сложно найти два таких сообщения, которые не равны,
но у них равны хеш-коды.
4. Стойкость к удлинению прообраза: хеш-функция не должна быть хорошо аддитируема. Если
злоумышленник не знает сообщение, но знает его длину и хеш-код от него, то ему должно быть
сложно подобрать такое сообщение, которое, будучи дописанным к оригинальному, даст какуюнибудь известную хеш-функцию. Т.е., не должно быть возможно злоумышленнику что-то менять
путем дополнения в сообщении, получая известный выход.
10
11.
Примеры1. Класс функций сжатия XSPL на основе метода Меркла-Дамгора обработки сообщения по блокам. К
данному классу относится алгоритм ГОСТ Р 34.11-2012 («Стрибог»).
2. Класс функций сжатия SHA (SHA-0, SHA-1, SHA-2, SHA-3, SHA-256, SHA-512). Разработки США.
3. Устаревшие алгоритмы сжатия MD-4 и MD-5. Утратили криптографическую стойкость.
4. CRC32. Криптографически не стойкие.
Пусть есть файл-сообщение. Злоумышленник хочет внедрить в него вирус. Если для файла
выложен не стойкий с криптографической точки зрения код CRC32, то можно внедрить вирус в файл и
дополнительно поменять файл таким образом, чтобы CRC совпали с предыдущим файлом. Более того,
например CRC32 (32 бита на выходе) вскрывается полным перебором.
11
12.
CRC - полиномиальная арифметикаCRC основан на делении с остатком двоичных многочленов, то есть многочленов над конечным
полем. Код CRC – это остаток от деления многочлена, соответствующего входным данным, на некий
фиксированный (порождающий) многочлен.
Делитель
и делимое (сообщение) представляют в виде полиномов с двоичными
коэффициентами или в виде строки бит, каждый из которых является коэффициентом полинома.
Например:
десятичное число 23 в шестнадцатеричной системе счисления имеет вид 17, а в двоичном – 10111,
что совпадает с полиномом:
или, упрощенно:
1*x^4 + 0*x^3 + 1*x^2 + 1*x^1 + 1*x^0
x^4 + x^2 + x^1 + x^0
12
13.
CRC представление полиномов13
14.
В CRC используется XOR(арифметика без переносов)
10011011
+ 11001010
-------01010001
Если сообщение при передаче было повреждено, то мы получим сообщение XOR(T, E), где E –
это вектор ошибки. Получив сообщение, приемник делит XOR(T, E) на G. T mod G = 0.
Задача состоит в том, чтобы найти такие классы G, произведения которых будут как можно меньше
похожи на шумы в канале передачи (которые и вызывают повреждение сообщения).
14
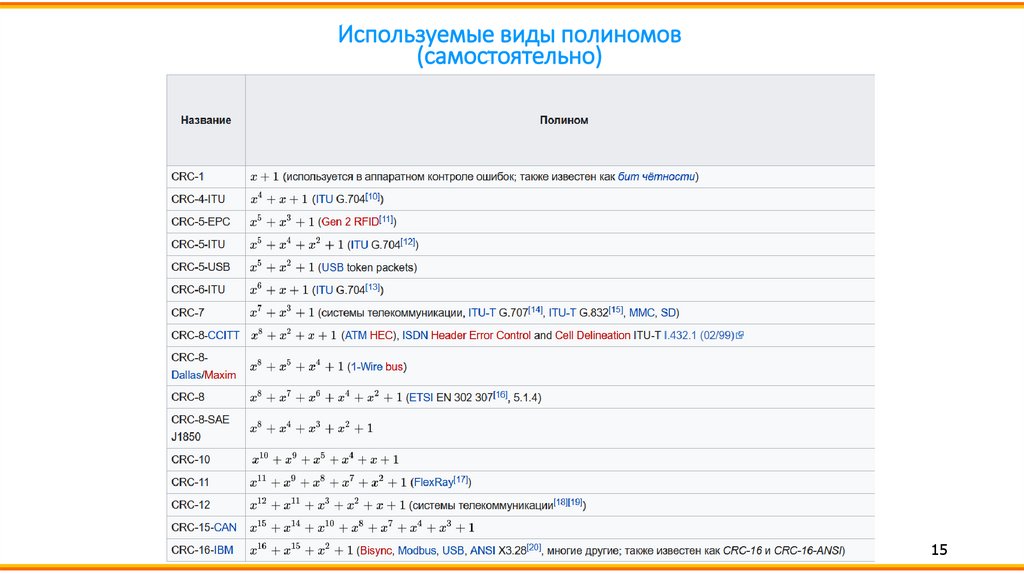
15.
Используемые виды полиномов(самостоятельно)
15
16.
Прямая реализация CRCЗагрузим регистр нулевыми битами
Дополним хвостовую часть сообщения W нулевыми битами
While (пока еще есть необработанные биты)
Begin
Сдвинем регистр на 1 бит влево и поместим очередной
еще не обработанный бит из сообщения в 0 позицию регистра.
If (из регистра был выдвинут бит со значением "1")
Регистр = Регистр XOR Полином
End
Теперь в регистре содержится остаток
16
17.
Прямая реализация CRC17
18.
Задачаpublic class CRC
{
public static int CRCflag(BitArray _message, BitArray _poly)//вычисление флага, показывающего, что при делении
сообщения с остатком получился 0
{
}
public static BitArray CRCXor(BitArray _message, BitArray _poly)//деление сообщения на полином, порядок бит - bigendian
{
//деление полиномов
}
public static BitArray CRCRem(BitArray _message, BitArray _poly)//вычисление остатка от деления на полином
{
}
}
18

















 informatics
informatics








