Similar presentations:
Алгоритмизация и программирование. Тема 2.1. Понятие алгоритма и сущность алгоритмизации вычислительного процесса
1.
2.
Понятие алгоритмаОтносится к числу фундаментальных понятий математики
и информатики и является объектом исследования
специального раздела – теории алгоритмов.
Происходит от имени узбекского математика Абу Джафара
Мухаммада ибн-Муса аль-Хорезми (VIII – IX в).
Алгоритмом называется некоторая последовательность
точных предписаний (правил), однозначно определяющая
процесс преобразования исходных данных и
промежуточных результатов в конечный результат при
решении всех задач данного типа.
3.
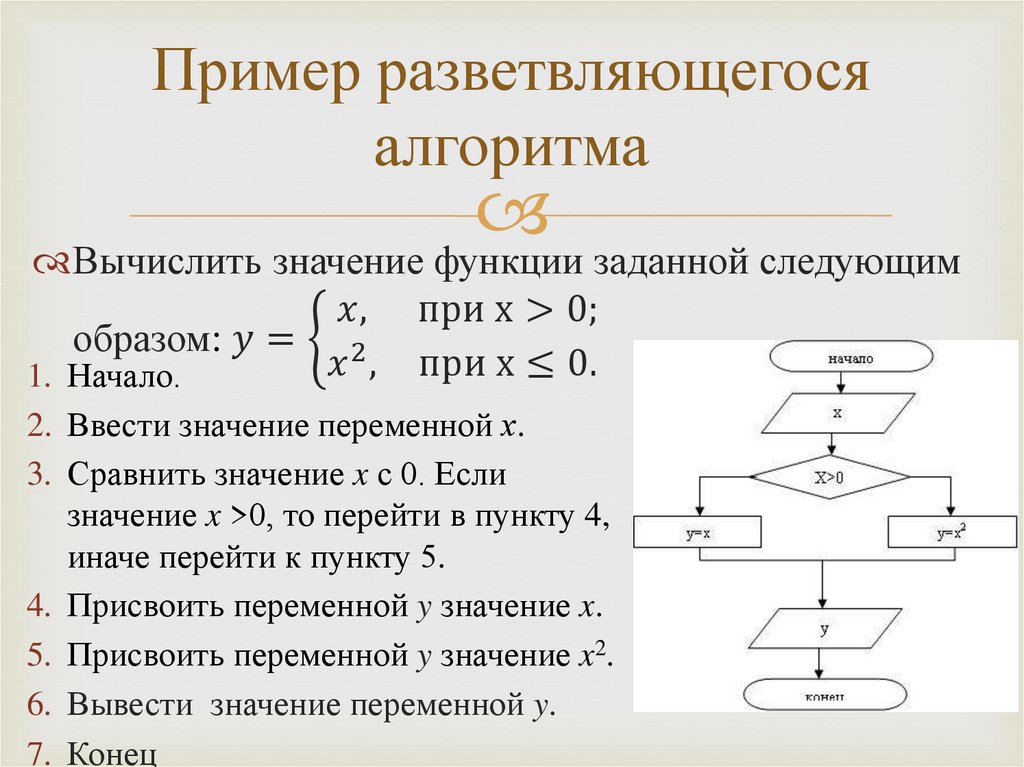
Пример 2.1При переходе через проезжую часть дороги на
перекрестке нужно руководствоваться
следующей последовательностью предписаний:
1. Подойти к краю проезжей части, не заходя на нее.
2. Посмотреть на сигнал светофора, предназначенного для
оповещения пешеходов.
3. Если горит красный сигнал светофора, то остановиться.
В противном случае перейти к выполнению п. 5.
4. Дождаться зеленого сигнала светофора и перейти к
выполнению п. 5.
5. Перейти через проезжую часть.
4.
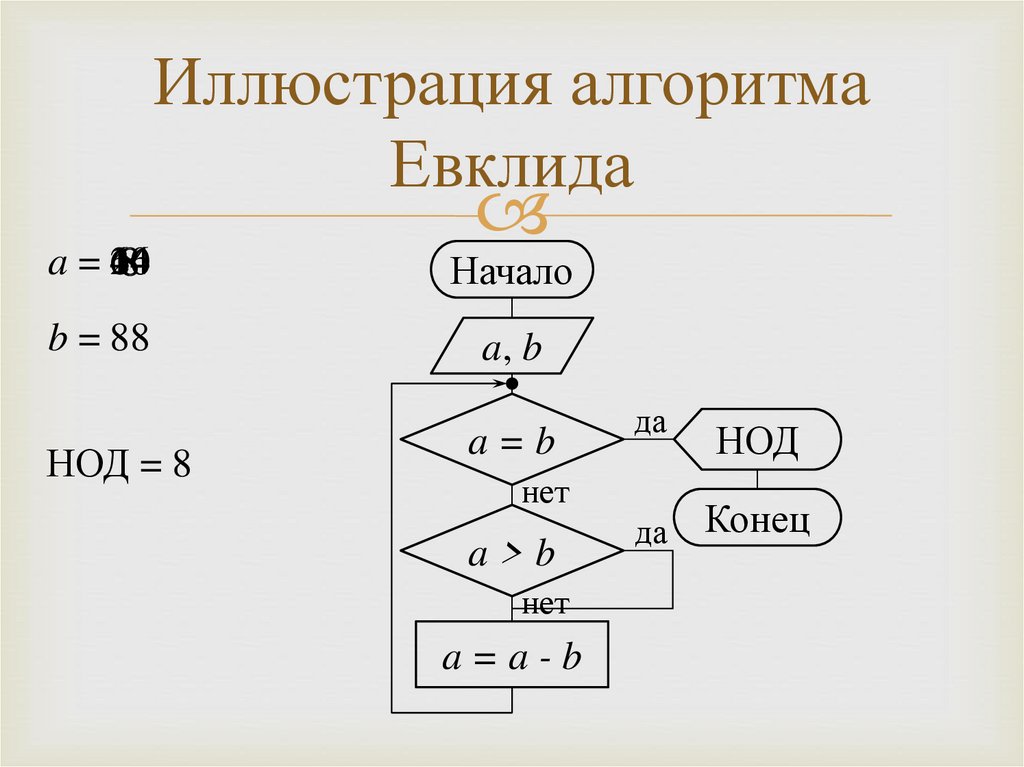
Пример 2.2 (алгоритм Евклида)1. Если a = b, то перейти к п. 4, в противном случае –
к п. 2.
2. Если a > b, то перейти к п. 3. В противном случае
поменять значения a и b местами и также перейти
к п. 3.
3. Вычесть число b из числа a, обозначить
полученную сумму снова буквой a и вернуться
к выполнению п. 1.
4. Считать НОД любое из чисел a или b. Конец.
5.
Иллюстрация алгоритмаЕвклида
a = 16
64
40
24
8
Начало
b = 88
a, b
НОД = 8
a=b
да
нет
a>b
нет
a=a-b
да
НОД
Конец
6.
Пример 2.3 («решетоЭратосфена»)
1. Выписать последовательно все целые положительные числа
от 2 до n.
2. Присвоить переменной p значение 2, соответствующее
первому простому числу.
3. Если p ≤ n, то перейти к п. 4, в противном случае – к п. 6.
4. Последовательно вычеркнуть числа 2p, 3p, 4p, …, kp.
При этом число k должно быть выбрано таким образом, чтобы
kp ≤ n, а (k+1)p > n.
5. Определить наименьшее число, которое не было вычеркнуто,
присвоить его переменной p, а затем вернуться к п. 3.
6. Все числа, которые остались невычеркнутыми, и являются
простыми. Конец.
7.
Иллюстрация «решетаЭратосфена» при n = 35
2
3
4 числа
5
Простые
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
8.
Этапы алгоритмическогопроцесса
1. Постановка задачи
2. Построение математической модели
3. Разработка алгоритма (алгоритмизация)
выделение автономных этапов вычислительного процесса
формальная запись содержания выделенных этапов
определение порядка следования этапов
проверка правильности выбранного алгоритма
4. Реализация алгоритма (составление программы)
5. Анализ алгоритма и его сложности
условная длина L n1 log 2 n1 n2 log 2 n2
условный объем V L log 2 n1 n2
6. Исполнение, тестирование и отладка программы
7. Анализ и обработка результатов вычислений
8. Документирование и сопровождение алгоритма и программы
9.
10.
ОпределенияИсполнитель алгоритма – человек или
группа людей, робот, станок, компьютер, язык
программирования и т. д., реализующий
процесс решения задачи в соответствии
с алгоритмом
Система команд исполнителя –
совокупность команд, которые способен
выполнять исполнитель алгоритма
11.
Исполнитель-роботРабочее поле
Исполнитель-робот
Склад
Система команд исполнителя:
ВПЕРЕД – переход на одну клетку в
направлении ориентации
ВПРАВО – поворот на месте на 90° по
часовой стрелке
ВЛЕВО – поворот на месте на 90°
против часовой стрелки
ВЗЯТЬ – захват объекта; при этом
робот должен находиться в той же
клетке, что и объект
УСТАНОВИТЬ – установка объекта в
данной клетке поля
12.
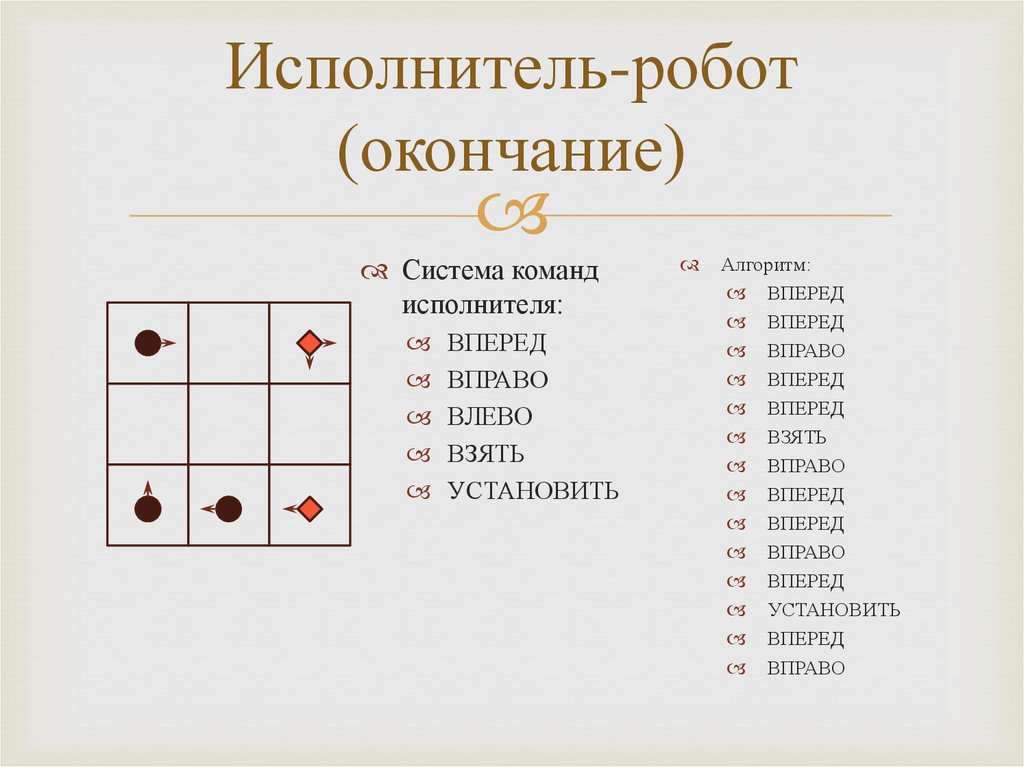
Исполнитель-робот(продолжение)
Разработать для исполнителя-робота алгоритм
перемещения объекта со склада в среднюю клетку
рабочего поля, находящуюся в нижнем ряду. По
завершении работы робот должен занять исходное
положение
13.
Исполнитель-робот(окончание)
Система команд
исполнителя:
ВПЕРЕД
ВПРАВО
ВЛЕВО
ВЗЯТЬ
УСТАНОВИТЬ
Алгоритм:
ВПЕРЕД
ВПЕРЕД
ВПРАВО
ВПЕРЕД
ВПЕРЕД
ВЗЯТЬ
ВПРАВО
ВПЕРЕД
ВПЕРЕД
ВПРАВО
ВПЕРЕД
УСТАНОВИТЬ
ВПЕРЕД
ВПРАВО
14.
15.
Свойства алгоритмовДискретность – свойство алгоритма,
означающее возможность разбиения алгоритма
на отдельные элементарные этапы,
выполняющиеся в строго определенном
порядке. Характерно лишь для
последовательных алгоритмов.
Понятность – свойство алгоритма, означающее
способность исполнителя понять предписания,
заложенные в алгоритме, и выполнить их.
16.
Свойства алгоритмов(продолжение)
Определенность – свойство алгоритма,
означающее возможность однозначной
трактовки любого шага алгоритма независимо
от исполнителя.
Детерминированность – свойство алгоритма,
означающее возможность однозначной
трактовки любого шага алгоритма независимо
от исходных данных.
17.
Свойства алгоритмов(продолжение)
Массовость – свойство алгоритма,
означающее возможность его
применения для решения задачи при
различных значениях исходных данных.
Общность – свойство алгоритма,
означающее возможность его
применения для решения целого класса
однотипных задач.
18.
Свойства алгоритмов(продолжение)
Результативность (потенциальная
выполнимость) – свойство алгоритма,
означающее возможность завершения
алгоритмического процесса и получения
искомого результата за конечное число
шагов.
19.
Свойства алгоритмов(окончание)
Правильность – свойство алгоритма,
означающее способность обеспечивать
получение именно того результата, который
требуется определить в соответствии с
постановкой задачи.
Эффективность – свойство алгоритма,
означающее наименьшую продолжительность
решения задачи или наименьший расход
компьютерной памяти по сравнению со всеми
другими алгоритмами.
20.
21.
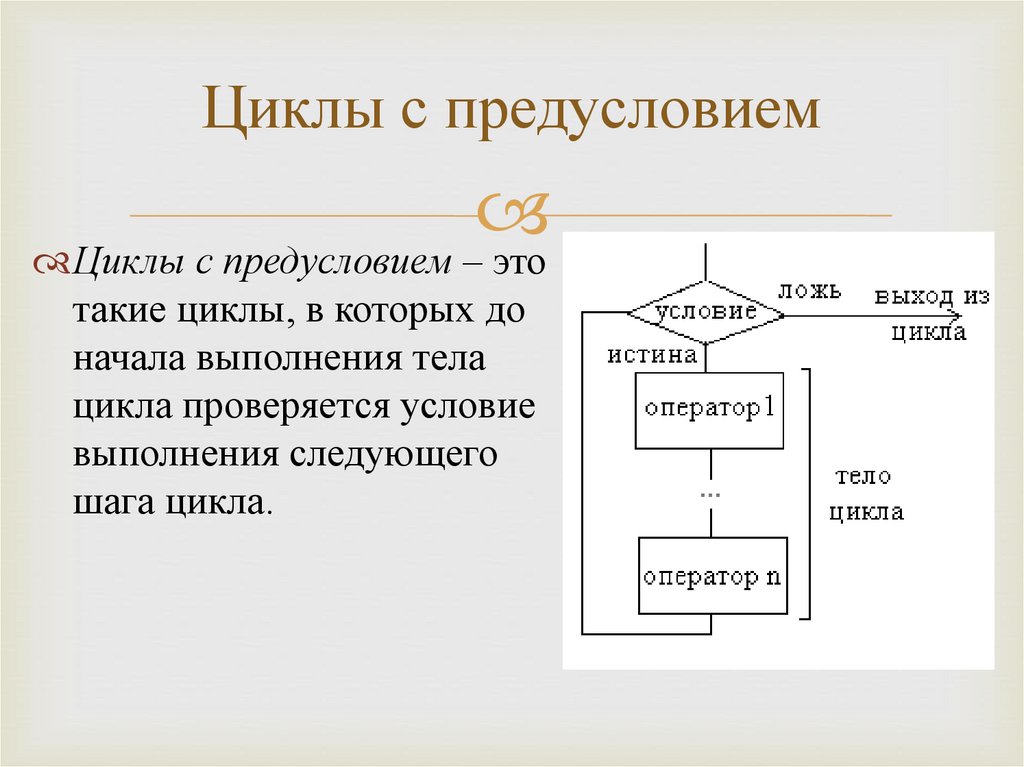
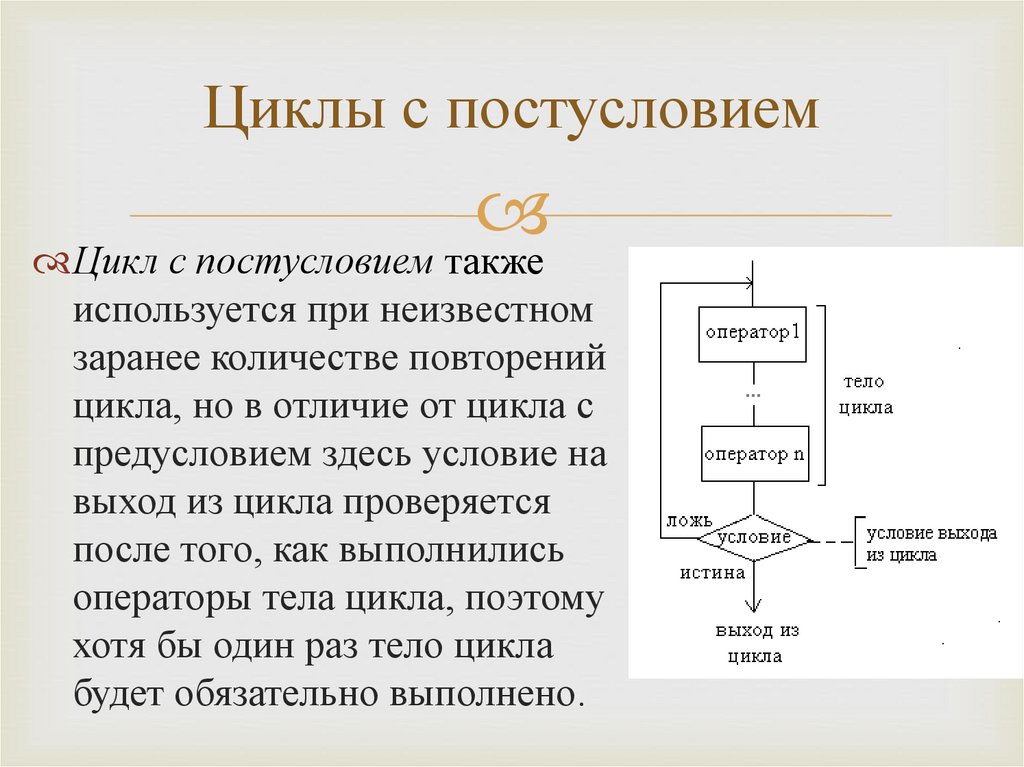
2.4.1. Вербальнаязапись алгоритма
Самой распространенной формой представления
алгоритмов, адресуемых человеку, является
обычная вербальная запись.
Содержание последовательных этапов вычислений
задается в произвольной форме на естественном
языке, но с тщательно отобранным набором слов.
Недостаток: отсутствие более или менее строгой
формализации и наглядности вычислительного
процесса.
22.
Пример вербальной записиалгоритма
Найти:
x 4
y
2
3x 1
1.Определить для переменной х конкретное числовое значение.
2.Умножить х на 3.
3.Из результата второго действия извлечь квадратный корень.
4.К результату третьего действия прибавить 1.
5.Умножить х на х.
6.Из результата пятого действия вычесть 4.
7.Результат шестого действия разделить на результат четвертого.
Полученное число считать значением переменной у.
23.
Пример вербальной записиалгоритма (после модификации)
x2 4
1. Начало.
y
2. Ввести значение переменной х.
3x 1
3. Переменной а присвоить значение выражения 3 х.
4. Переменной b присвоить значение выражения а.
5. Переменной с присвоить значение выражения b+1.
6. Переменной d присвоить значение выражения х х.
7. Переменной e присвоить значение выражения d-4.
8. Переменной y присвоить значение выражения e/c.
9. Вывести значение переменной у.
10. Конец
24.
Пример вербальной записиалгоритма (после модификации)
x2 4
y
3x 1
1. Начало.
2. Ввести значение переменной х. x = 12
3. Переменной а присвоить значение выражения 3 х. a = 36
a=6
4. Переменной а присвоить значение выражения а.
5. Переменной а присвоить значение выражения а +1. a = 7
6. Переменной y присвоить значение выражения х х. y = 144
7. Переменной y присвоить значение выражения y-4. y = 140
8. Переменной y присвоить значение выражения y/a. y = 20
9. Вывести значение переменной у.
20
10. Конец
25.
2.4.2. Формульно-вербальнаязапись алгоритма
Основан на задании предписаний о выполнении
конкретных действий в определенной
последовательности с использованием
математических формул и словесных пояснений.
Этот способ является общепринятым при описании
математических выкладок и доказательстве теорем.
26.
Пример формульно-вербальнойзапись алгоритма
Выражение
1
V h R 2 Rr r 2
3
задает объем усеченного конуса. Здесь h – высота
усеченного конуса, R и r – радиусы нижнего и
верхнего оснований соответственно.
27.
Формульно-вербальная записьалгоритма (продолжение)
При подобном способе записи алгоритма
достигается любая степень детализации
вычислительного процесса. Кроме того, этот способ
более компактен и нагляден по сравнению с
вербальным.
Недостаток: формула неоднозначно определяет
последовательность действий, т. е. нарушаются
свойства определенности и детерминированности.
28.
2.4.3.Табличная запись
алгоритма
Существует несколько типов таблиц, из которых мы
рассмотрим два наиболее простых типа.
Первый из них обычно используют при
организации вычислений по формуле с
пооперационной регистрацией промежуточных
результатов. Разбиение формулы на
последовательность элементарных действий и дает
последовательность предписаний алгоритма.
29.
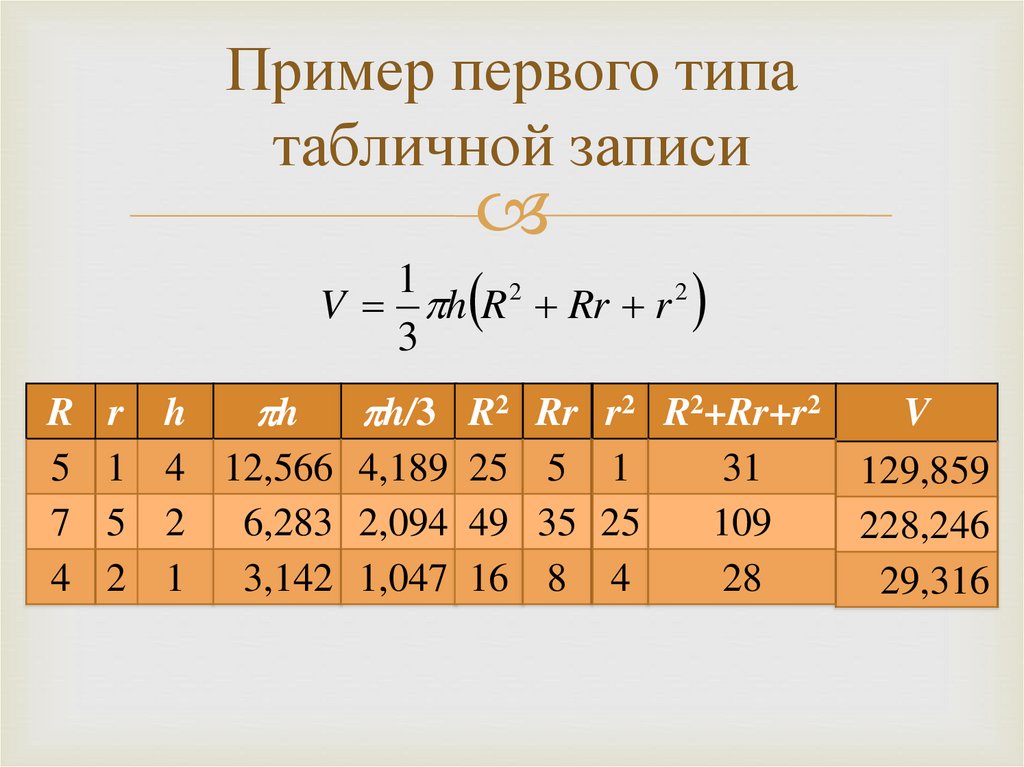
Пример первого типатабличной записи
1
2
2
V h R Rr r
3
R
5
7
4
r
1
5
2
h
h h/3 R2 Rr r2 R2+Rr+r2
V
4 12,566 4,189 25 5 1
31
129,859
2 6,283 2,094 49 35 25
109
228,246
1 3,142 1,047 16 8 4
28
29,316
30.
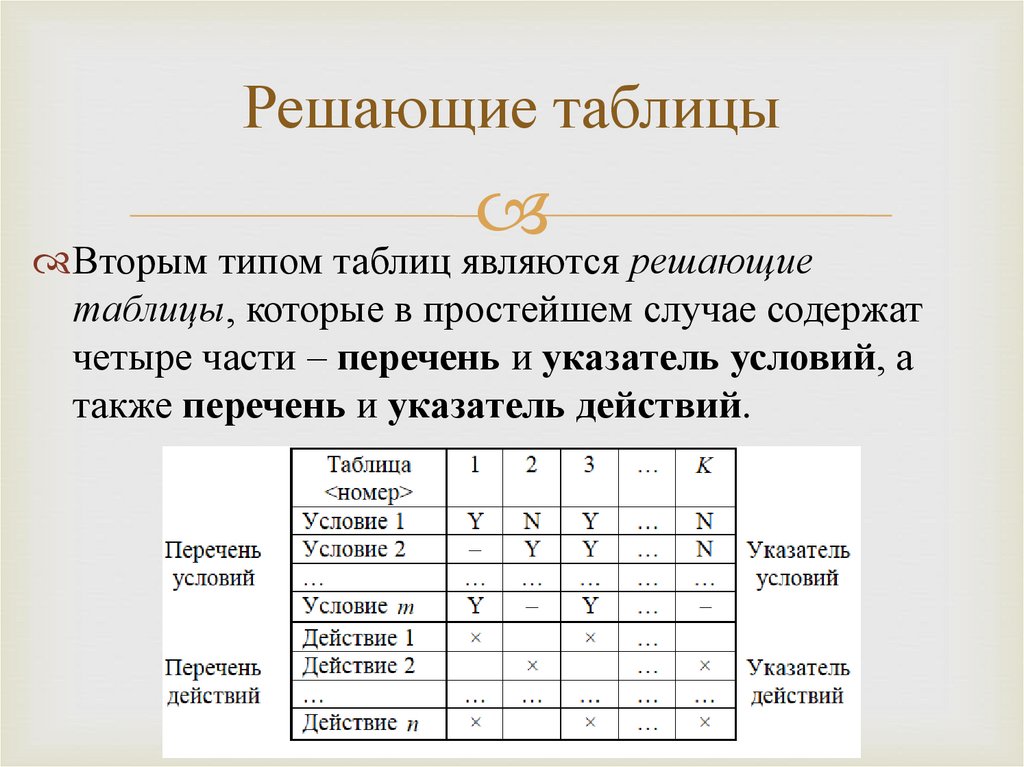
Решающие таблицыВторым типом таблиц являются решающие
таблицы, которые в простейшем случае содержат
четыре части – перечень и указатель условий, а
также перечень и указатель действий.
31.
Решающие таблицы(продолжение)
Если формулировка условий такова, что возможны
лишь два ответа – «да» или «нет», то таблицы
называются таблицами с ограниченными входами.
Если же предполагаемых ответов несколько, то
удобнее пользоваться таблицами с расширенными
входами. При этом простые условия записываются
так же, как и в таблицах с ограниченными входами,
начало сложного условия – в перечне условий, а его
продолжение распределяется между столбцами
указателя условий.
32.
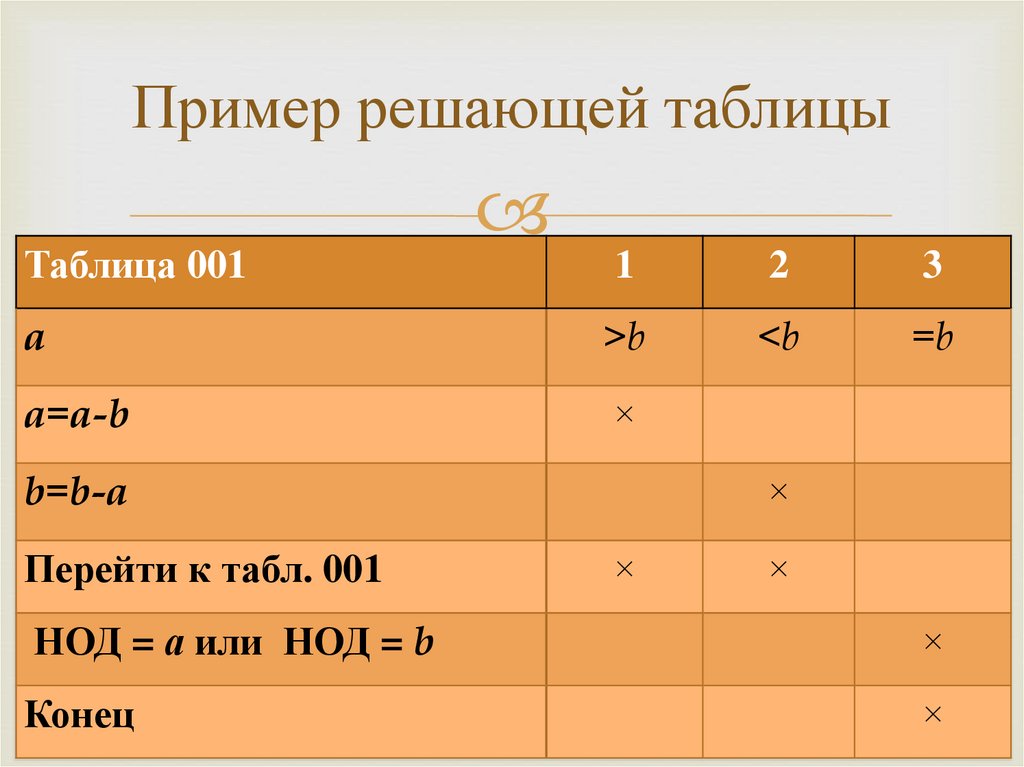
Пример решающей таблицыТаблица 001
1
2
3
a
>b
<b
=b
a=a-b
×
b=b-a
Перейти к табл. 001
×
×
×
НОД = а или НОД = b
×
Конец
×
33.
2.4.4. Запись алгоритма спомощью псевдокода
Псевдокод – это язык записи структурированных
алгоритмов.
Набор конструкций состоит из смеси
алгоритмического языка высокого уровня и фраз
родного языка исполнителя.
Псевдокод используется для облегчения разработки
программ. Алгоритм, написанный на псевдокоде,
достаточно легко преобразовать в программный
код.
34.
Пример записи алгоритма спомощью псевдокода
Задача нахождения наибольшего элемента из двух
натуральных чисел (А и В):
Начало
Ввод А, В
Если А≥В,
то max=A
иначе max=B
Конец Если
Вывод max
Конец
35.
Достоинства псевдокодаОсновными достоинствами псевдокода являются:
близость к языкам программирования;
возможность разобраться в самом длинном и
сложном алгоритме, поэтому псевдокод используется
чаще всего для документирования программ.
36.
2.4.5. Графическая записьалгоритмов
Блок-схема алгоритма – графическое представление метода
решения задачи, в котором используются символы,
отображающие операции и данные.
В схеме алгоритма каждому типу действий соответствует
геометрическая фигура, представленная символом
действия, – блоков. Связь между блоками изображают с
помощью линий, называемых линиями связи, обозначающих
передачу управления, которые также определяют
очерёдность выполнения действий.
Правила составления блок-схем установлены ЕСПД ГОСТ
19.701-90 "Схемы алгоритмов, программ, данных и систем.
Обозначения условные и правила выполнения".
37.
Правила составления блок-схем1.Каждая блок-схема должна иметь блок «Начало» и один
блок «Конец».
2.«Начало» должно быть соединено с блоком «Конец»
линиями потока по каждой из имеющихся на блок-схеме
ветвей.
3.В блок-схеме не должно быть блоков, кроме блока «Конец»,
из которых не выходит линия потока, равно как и блоков, из
которых управление передается «в никуда».
4.Блоки должны быть пронумерованы. Нумерация блоков
осуществляется сверху вниз и слева направо, номер блока
ставится вверху слева, в разрыве его начертания.
38.
Правила составления блок-схем(продолжение)
5.Блоки связываются между собой линиями потока,
определяющими последовательность выполнения блоков.
Линии потоков должны идти параллельно границам листа.
Если линии идут справа налево или снизу вверх, то стрелки в
конце линии обязательны, в противном случае их можно не
ставить.
6.По отношению к блокам линии могут быть входящими и
выходящими. Одна и та же линия потока является выходящей
для одного блока и входящей для другого.
7.От блока «Начало» в отличие от всех остальных блоков линия
потока только выходит, так как этот блок – первый в блоксхеме.
39.
Правила составления блок-схем(продолжение)
8. Блок «Конец» имеет только вход, так как это последний блок в
блок-схеме.
9. Для простоты чтения желательно, чтобы линия потока входила в
блок «Процесс» сверху, а выходила снизу.
10.Чтобы не загромождать блок-схему сложными
пересекающимися линиями, линии потока можно разрывать.
При этом в месте разрыва ставятся соединители, внутри которых
указываются номера соединяемых блоков. В блок-схеме не
должно быть разрывов, не помеченных соединителями.
11.Чтобы не загромождать блок, можно информацию о данных, об
обозначениях переменных и т.п. размещать в комментариях к
блоку.
40.
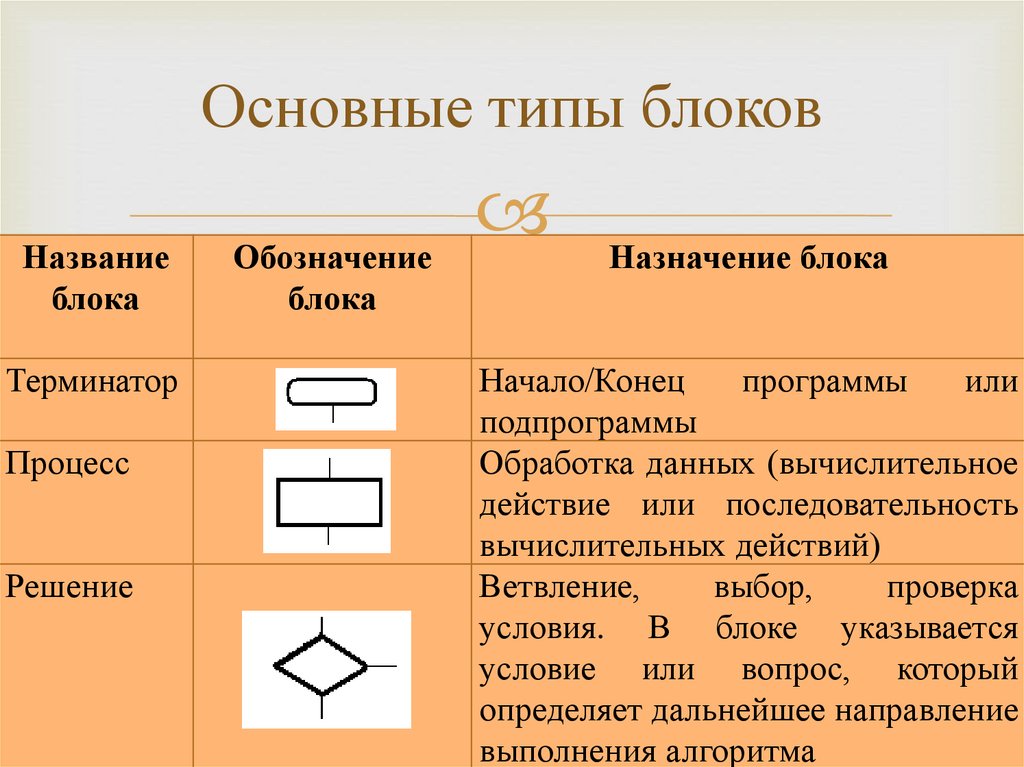
Основные типы блоковНазвание
блока
Терминатор
Процесс
Решение
Обозначение
Назначение блока
блока
Начало/Конец
программы
или
подпрограммы
Обработка данных (вычислительное
действие или последовательность
вычислительных действий)
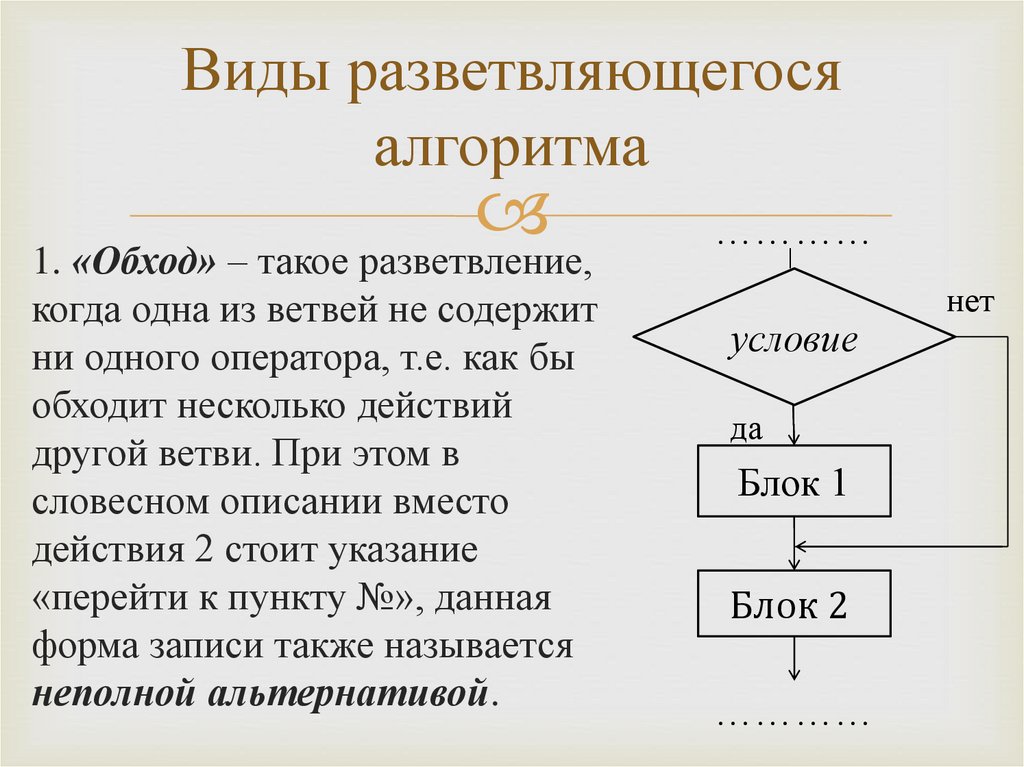
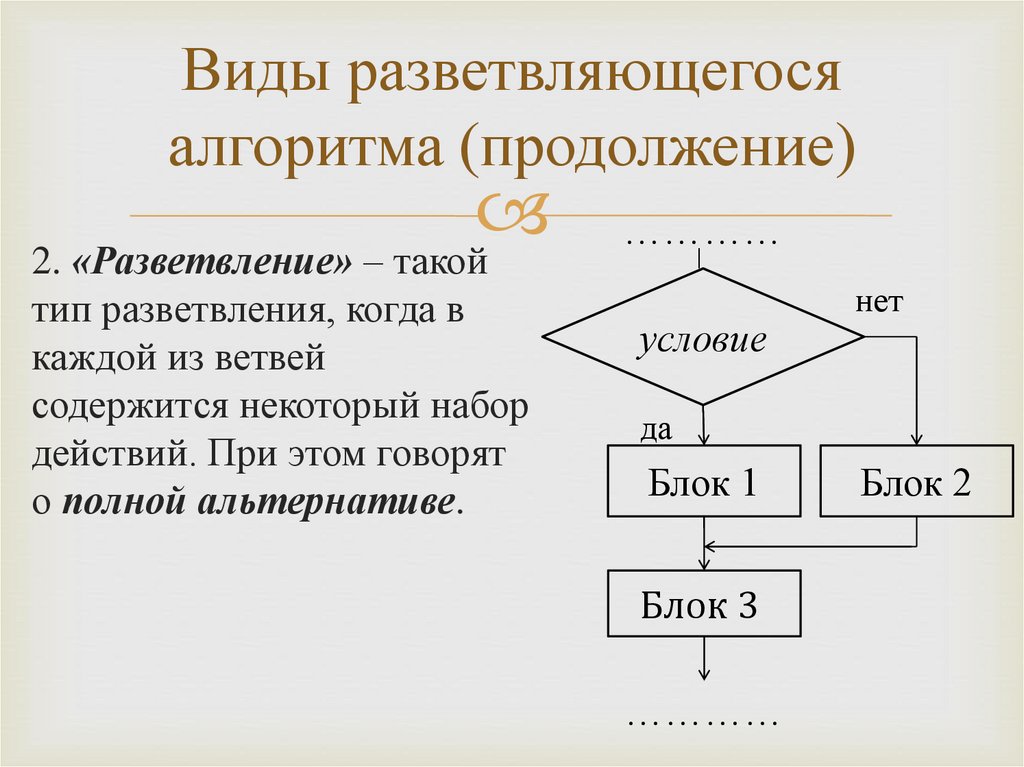
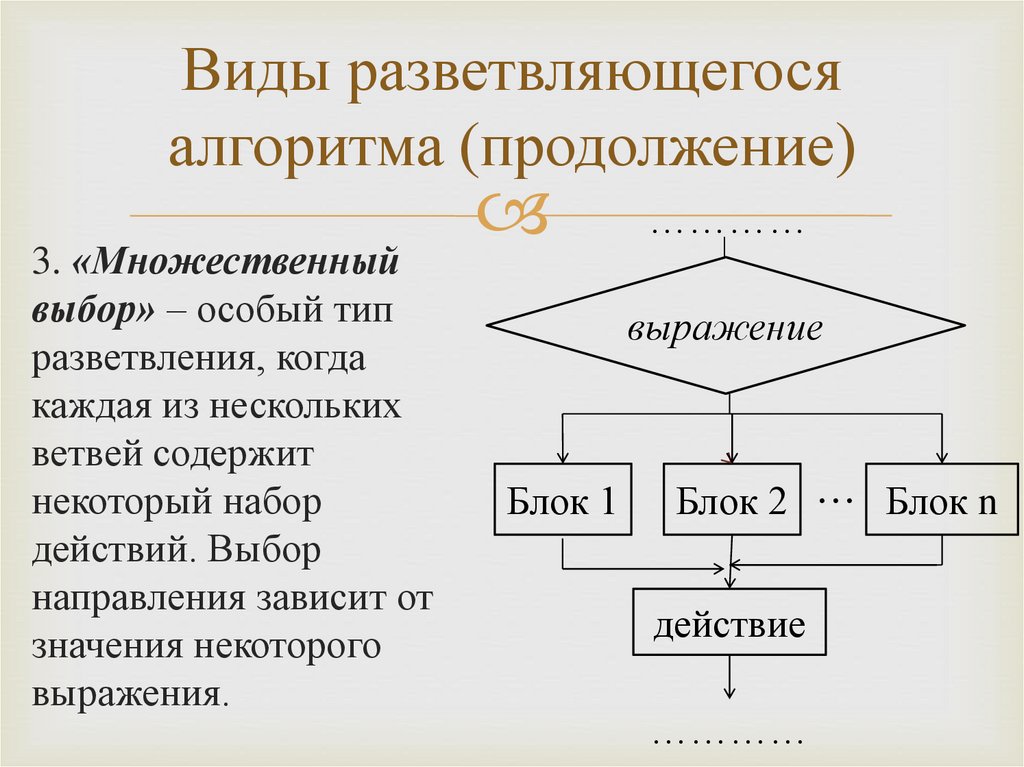
Ветвление,
выбор,
проверка
условия. В блоке указывается
условие или вопрос, который
определяет дальнейшее направление
выполнения алгоритма
41.
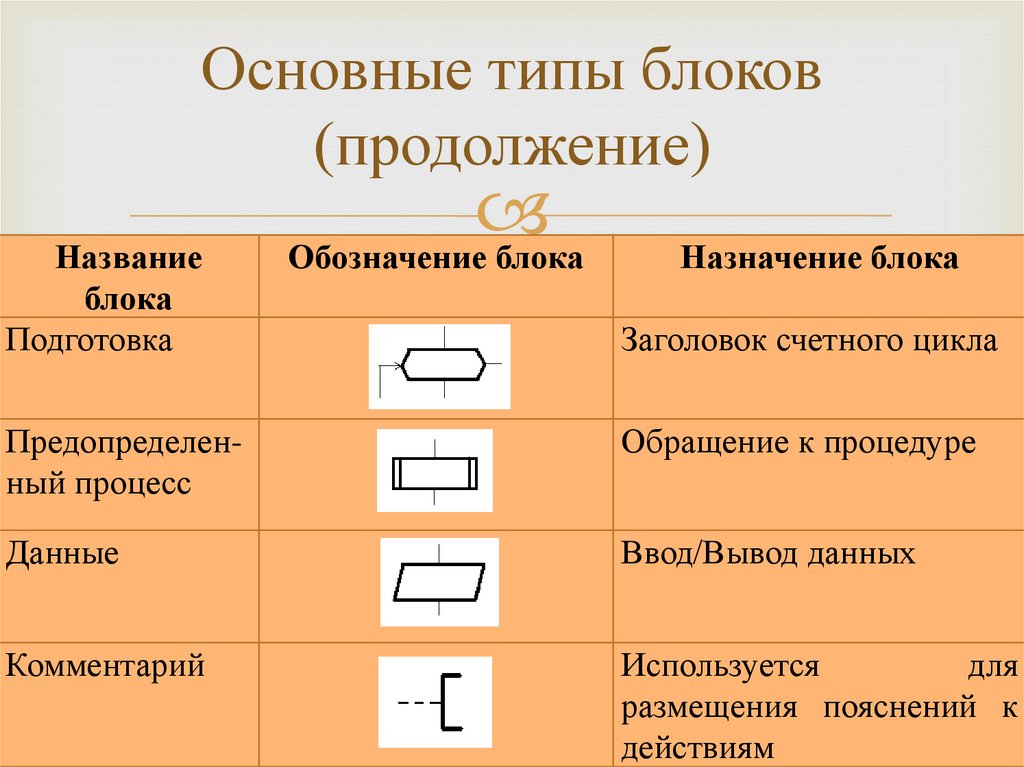
Основные типы блоков(продолжение)
Название
блока
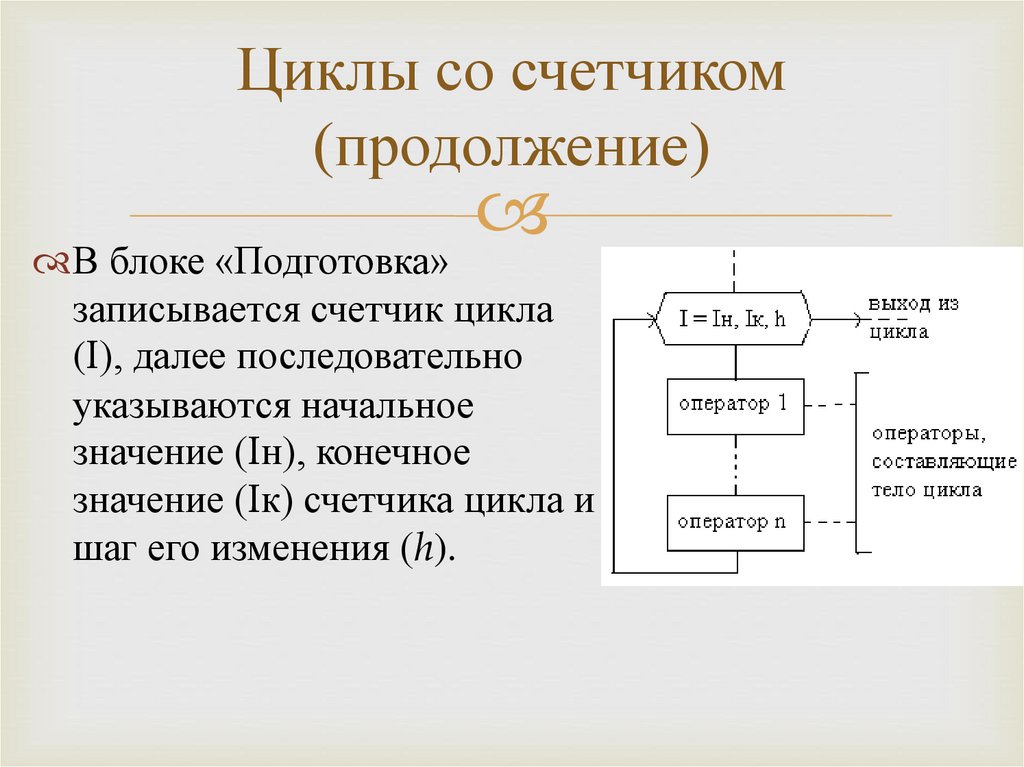
Подготовка
Обозначение блока
Назначение блока
Заголовок счетного цикла
Предопределенный процесс
Обращение к процедуре
Данные
Ввод/Вывод данных
Комментарий
Используется
для
размещения пояснений к
действиям
42.
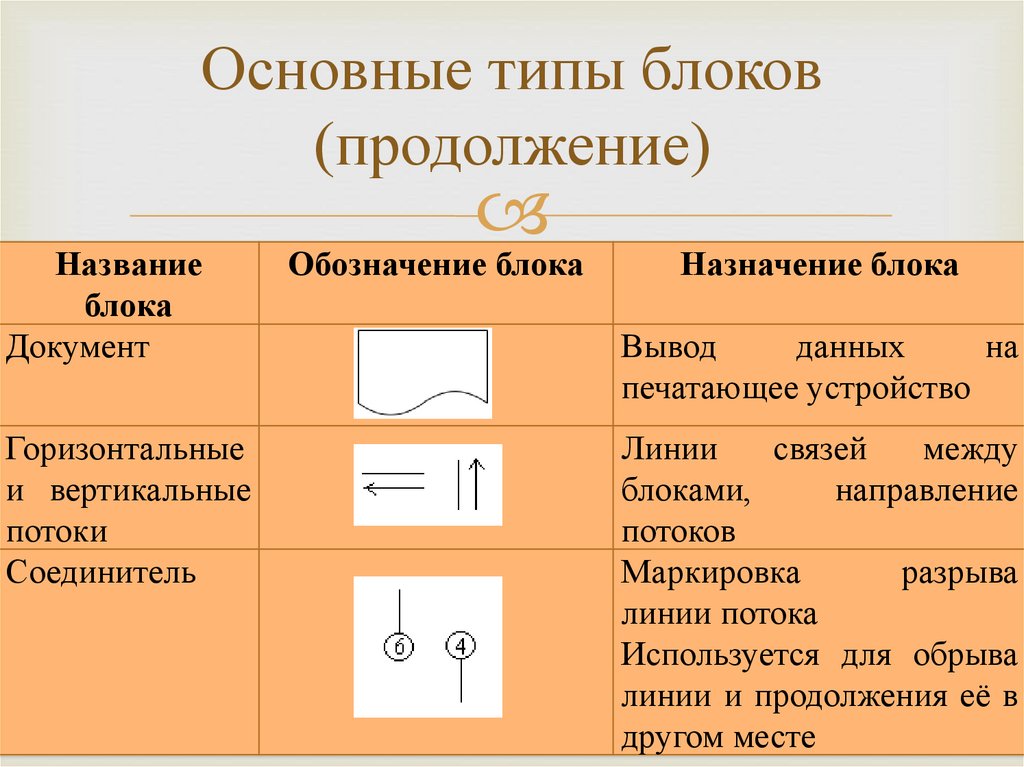
Основные типы блоков(продолжение)
Название
блока
Документ
Горизонтальные
и вертикальные
потоки
Соединитель
Обозначение блока
Назначение блока
Вывод
данных
на
печатающее устройство
Линии
связей
между
блоками,
направление
потоков
Маркировка
разрыва
линии потока
Используется для обрыва
линии и продолжения её в
другом месте
43.
44.
2.5.1. Линейный алгоритмЛинейный алгоритм состоит из
упорядоченной последовательности
действий, не зависящей от значений
исходных данных, при этом каждая
команда выполняется только один раз
строго после той команды, которая ей
предшествует. Такой порядок
выполнения действий называется
естественным.
Начало
Блок 1
Блок 2
…………
Конец
45.
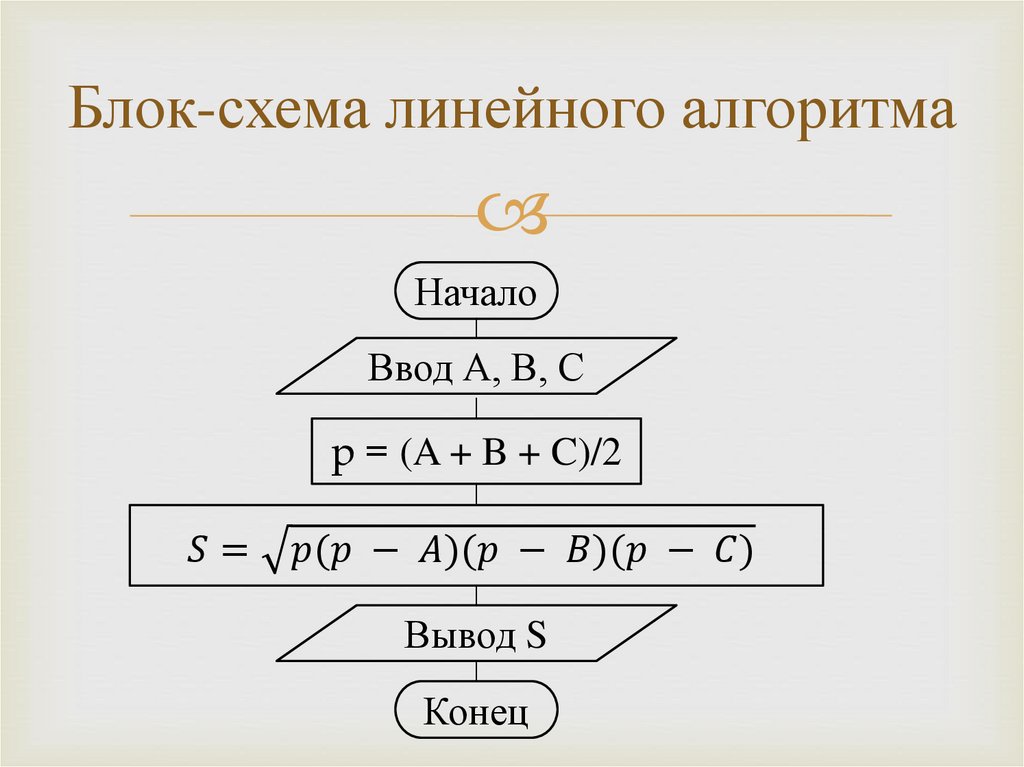
Пример линейного алгоритмаСоставить алгоритм вычисления площади
треугольника со сторонами A, B, C по формуле
Герона: S p (p - A) (p - B) (p - C)
Начало.
Ввести значение переменных A, B, C.
Переменной p присвоить значение выражения (A + B + C)/2.
Переменной S присвоить значение выражения
p (p - A) (p - B) (p - C)
5.Вывести значение переменной S.
6. Конец
1.
2.
3.
4.
46.
Блок-схема линейного алгоритмаНачало
Ввод А, В, С
p = (A + B + C)/2


















































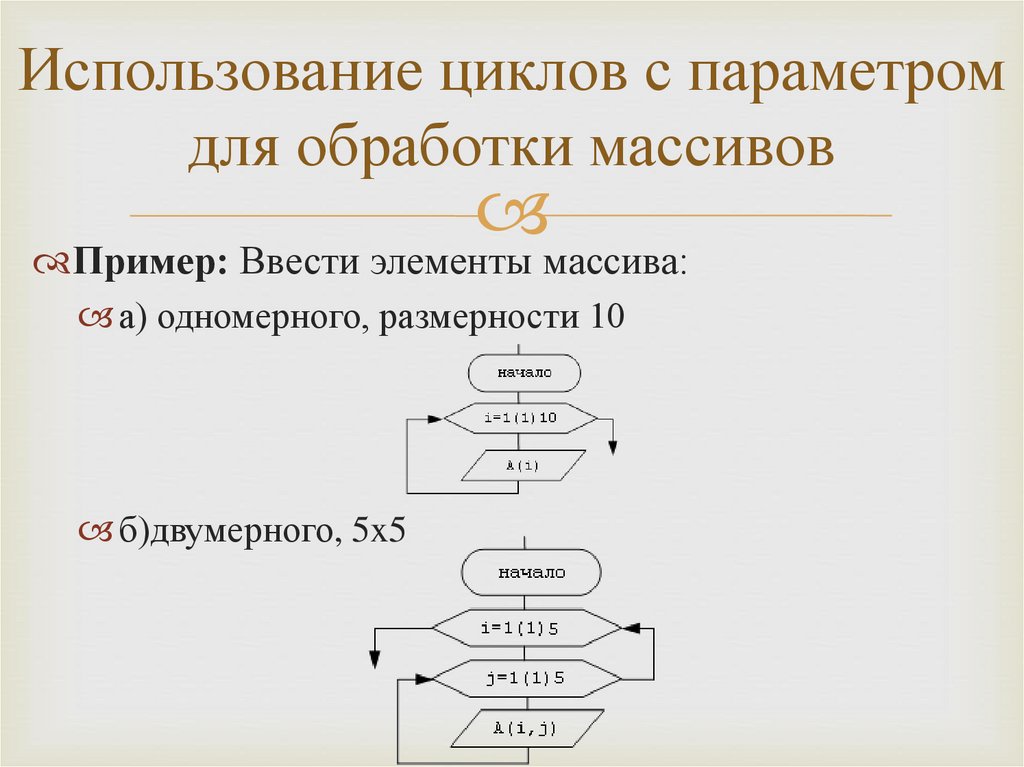













 programming
programming








