Разновидности графов

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Разновидности графов
Часть графа – это граф, содержащий часть узлов исходного
графа и часть (любую) его дуг {1}.
Подграфом графа называется такая его часть, которая вместе
со всякой парой узлов содержит и дугу, если она есть в
исходном графе{2}.
Суграф содержит все узлы исходного графа и часть его дуг
{3}.
1
2
3

11.

12.

13.

Построение матрицы смежности графа
неориентированного
ориентированного
вершины
вершины

14.

Матрица смежности взвешенного
графа
Взвешенный граф – это граф у которого с каждой дугой связано некоторое значение
называемое весом.

15.

16.

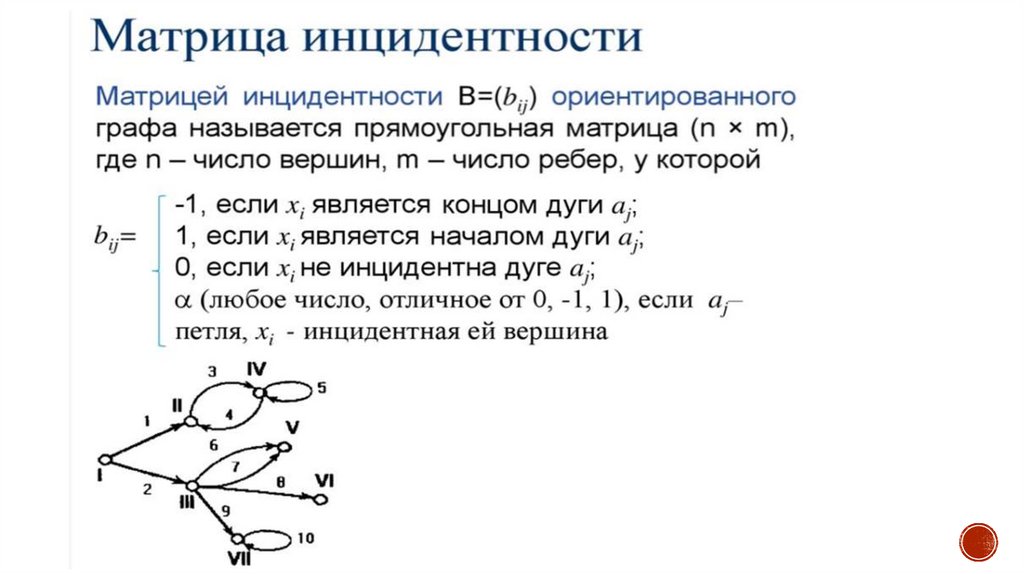
Построение матрицы инцидентности
неориентированного графа

17.

18.

Построение матрицы инцидентности
ориентированного графа

19.

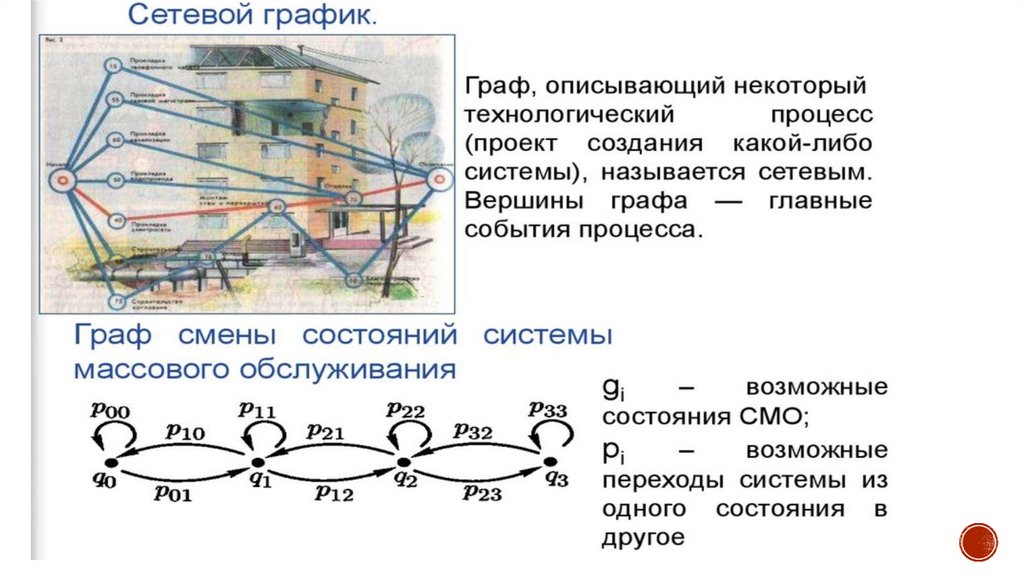
Обходы графа
Обход графа — это переход от одной его вершины к другой в поисках свойств
связей этих вершин, выполняется двумя основными алгоритмами :
поиск в глубину (Depth-First Search, DFS)
DFS следует концепции «погружайся глубже, головой вперед» («go deep, head first»).
Идея заключается в том, что мы двигаемся от начальной вершины (точки, места) в
определенном направлении (по определенному пути) до тех пор, пока не достигнем
конца пути или пункта назначения (искомой вершины). Если мы достигли конца пути,
но он не является пунктом назначения, то мы возвращаемся назад (к точке
разветвления или расхождения путей) и идем по другому маршруту.
поиск в ширину (Breadth-First Search, BFS).
BFS следует концепции «расширяйся» («go wide, bird’s eye-view»). Вместо того, чтобы
двигаться по определенному пути до конца, BFS предполагает движение вперед по
одному соседу за раз.

20.

Сравнение методов поисков графа
Поиск в глубину двигается по граням туда и обратно, а
поиск в ширину распространяется по соседям в поисках
цели.
Поиск в глубину использует стек, а поиск в ширину —
очередь.
Время выполнения обоих составляет общее время обхода
всех граней и всех вершин, а пространственная сложность
— зависит от количества вершин.

21.

Обходы графа
Применения алгоритма поиска в ширину
Поиск кратчайшего пути в невзвешенном графе (ориентированном или
неориентированном).
Нахождения решения какой-либо задачи (игры) с наименьшим числом ходов.
Найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин.
Найти все вершины, лежащие на каком-либо кратчайшем пути между заданной парой
вершин.
Применения алгоритма поиска в глубину
Поиск любого пути в графе.
Поиск лексикографически первого пути в графе.
Проверка, является ли одна вершина дерева предком другой.
Поиск наименьшего общего предка.
Топологическая сортировка.

22.

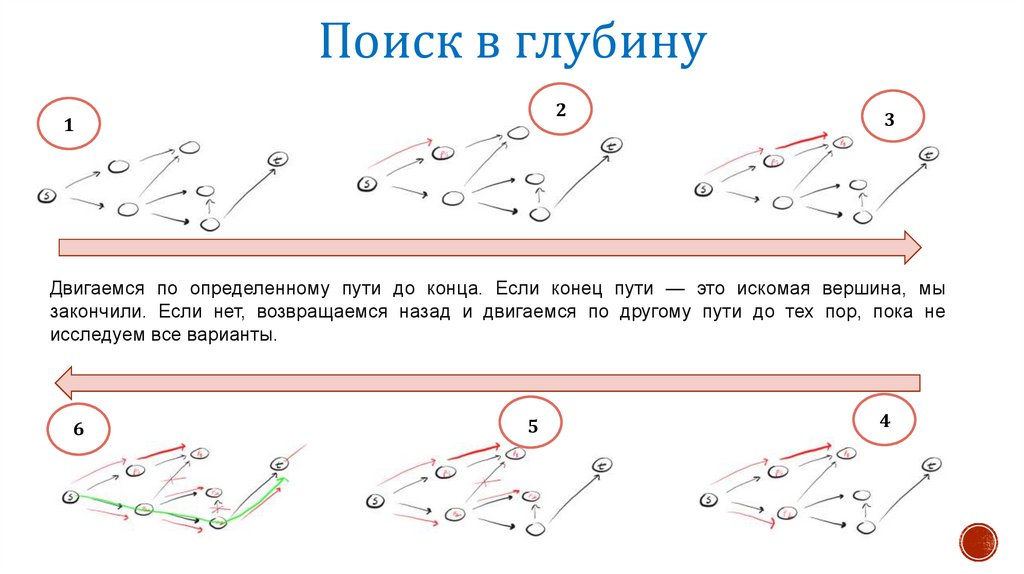
Поиск в глубину
2
1
3
Двигаемся по определенному пути до конца. Если конец пути — это искомая вершина, мы
закончили. Если нет, возвращаемся назад и двигаемся по другому пути до тех пор, пока не
исследуем все варианты.
6
5
4

23.

Алгоритм поиска графа в глубину
Стандартная реализация DFS помещает каждую вершину графа в одну из двух
категорий:
Посещенные.
Не посещенные.
Цель алгоритма - пометить каждую вершину, как посещенную, избегая циклов.
Алгоритм DFS работает следующим образом:
1)Начните с размещения любой вершины графа на вершине стека.
2)Возьмите верхний элемент стека и добавьте его в список посещенных.
3)Создайте список смежных узлов этой вершины. Добавьте те, которых нет в
списке посещенных, в начало стека.
4)Продолжайте повторять шаги 2 и 3, пока стек не станет пустым.

24.

Обход графа в глубину
Поиск в глубину предполагает продвижение вглубь
до тех пор, пока это возможно. Невозможность
продвижения означает, что следующим шагом будет переход
на последний, имеющий несколько вариантов движения
(один из которых исследован полностью), ранее посещенный
узел (вершина).
Отсутствие последнего исследуемого узла свидетельствует о
том, что все вершины графа уже просмотрены или
просмотрены вершины доступные из вершины, взятой в
качестве начальной.

25.

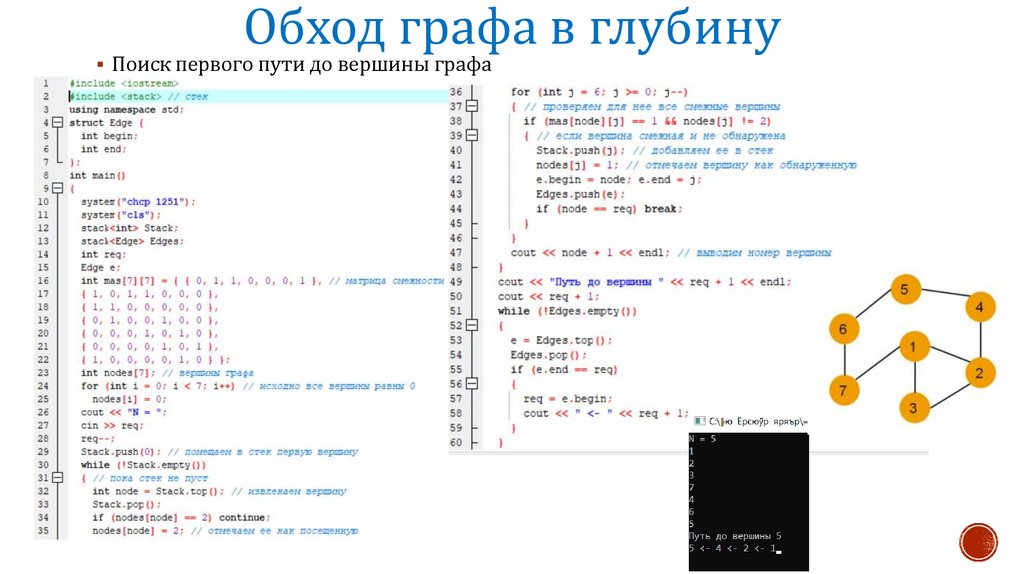
Обход графа в глубину
Поиск первого пути до вершины графа

26.

Обход графа в глубину
Рекурсивный поиск в глубину графа

27.

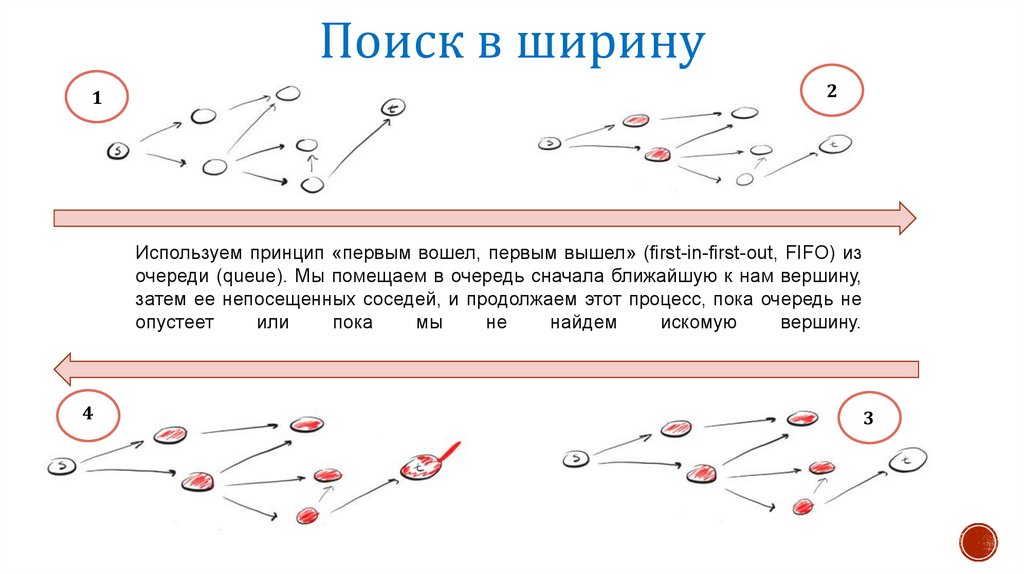
Поиск в ширину
1
2
Используем принцип «первым вошел, первым вышел» (first-in-first-out, FIFO) из
очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину,
затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не
опустеет
или
пока
мы
не
найдем
искомую
вершину.
4
3

28.

Алгоритм поиска графа в ширину
Стандартная реализация ВFS помещает каждую вершину графа в одну из двух
категорий:
Посещенные.
Не посещенные.
Цель алгоритма - пометить каждую вершину, как посещенную, избегая циклов.
Алгоритм работает следующим образом:
1)Начните с размещения любой вершины графа в конце очереди.
2)Возьмите передний элемент очереди и добавьте его в список посещенных.
3)Создайте список смежных узлов этой вершины. Добавьте те, которых нет в
списке посещенных, в конец очереди.
4)Продолжайте повторять шаги 2 и 3, пока очередь не опустеет.

29.

Обход графа в ширину
Происходит поуровневое посещение вершин графа:
•вначале посещается произвольно выбранный узел,
•затем – все потомки данного узла,
•после этого посещаются потомки потомков и т.д.
Вершины просматриваются в порядке возрастания их
расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин
графа, либо в случае выполнения требуемого условия.

30.

Обход графа в ширину
Поиск кратчайшего пути до вершины графа