Лингвистическая ТИ. Основы математической статистики. Тема 4

1.

Лингвистическая ТИ
Краткий конспект лекции

2.

Тема 4. Основы математической статистики
1. Лингвистическая статистика.
2. Основы описательной статистики.*
3. Средства визуализации данных.
4. Меры различий для несвязанных выборок.
5. Уровень значимости критерия.
6. Статистический анализ текстов.
* Савельев В. Статистика и котики

3.

1. Лингвистическая статистика
ЛИНГВИСТИЧЕСКАЯ СТАТИСТИКА
— это отрасль языкознания, занимающаяся
количественных характеристик языка и речи.
анализом
Лингвистическая
статистика
изучает
статистические
характеристики распределения лингвистических единиц в тексте
речи; на основе этих данных формируются высказывания о
системе языка и механизме порождения текста.

4.

1. Лингвистическая статистика
Различают:
фонологическую статистику,
морфологическую статистику,
лексическую статистику,
стилистическую статистику,
типологическую статистику,
хронологическую статистику (глоттохронологию).
Основное предположение:
любой лингвистической форме присуща априорная вероятность
быть употребленной в тексте.

5.

1. Лингвистическая статистика
Лингвистическая
статистика
лингвистических форм и их классов:
изучает
характеристики
относительные частоты,
размер (длина),
сочетаемость (сила связи),
распределение в тексте.
Индекс синтетичности – мера синтеза языка, отношение числа
морфем к числу слов в тексте:
вьетнамский язык (1,06),
эскимосский язык (3,72),
английский (1,68),
русский (1,90).

6.

1. Лингвистическая статистика
Отдельную отрасль лингвистической статистики составляют
исследования, использующие методы теории информации.
Лингвостатистические задачи:
нахождение объема словника текста по его длине,
нахождение объема полного словаря писателя по выборке из
текстов этого писателя,
оценка степени неоднородности текстов на разных уровнях,
характеристика статистической структуры текста,
установление связей между статистическими характеристиками
лингвистических форм разных уровней и др.

7.

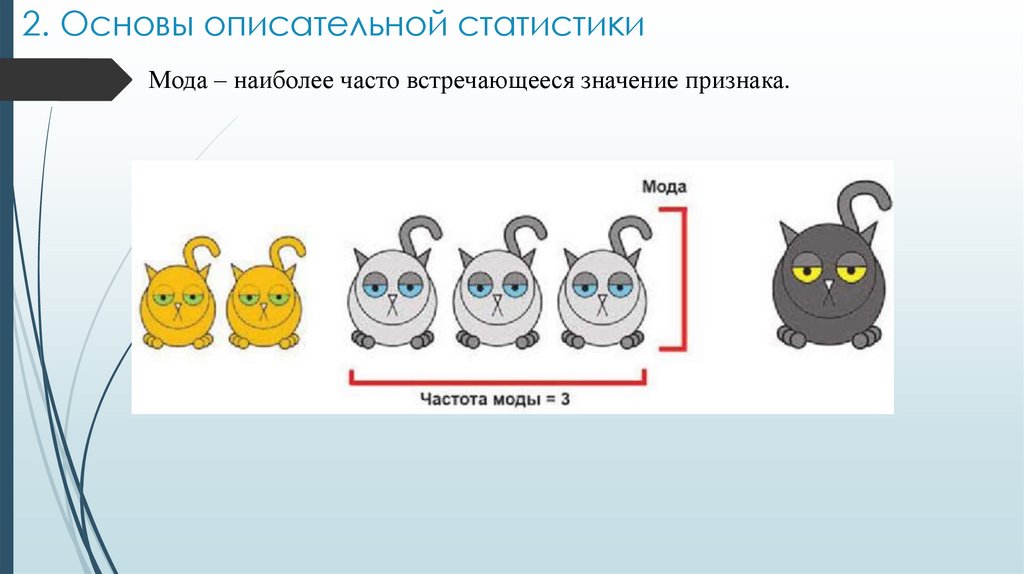
2. Основы описательной статистики
Мода – наиболее часто встречающееся значение признака.

8.

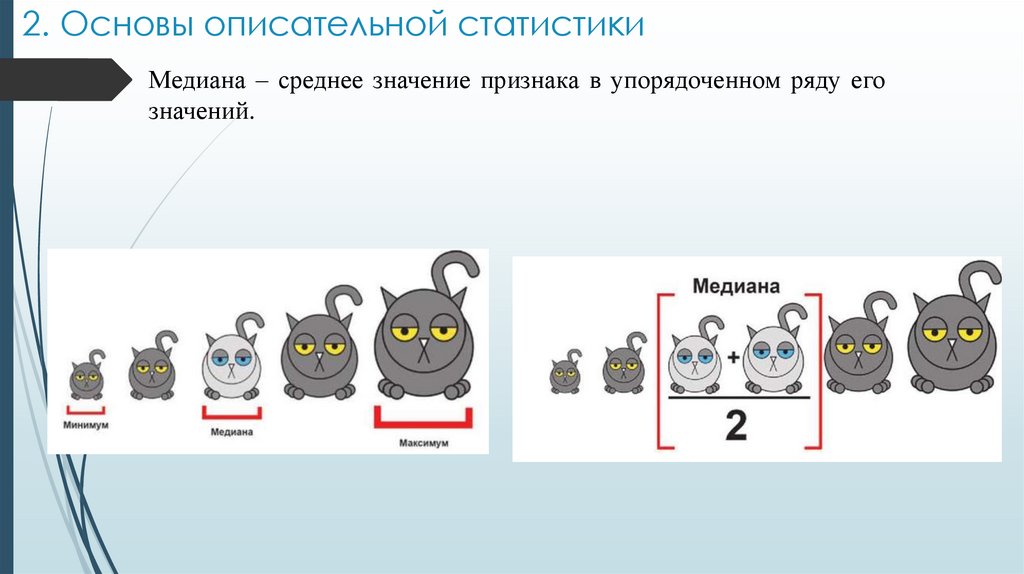
2. Основы описательной статистики
Медиана – среднее значение признака в упорядоченном ряду его
значений.

9.

2. Основы описательной статистики
Среднее значение – среднее арифметическое всех значений
признака в выборке.

10.

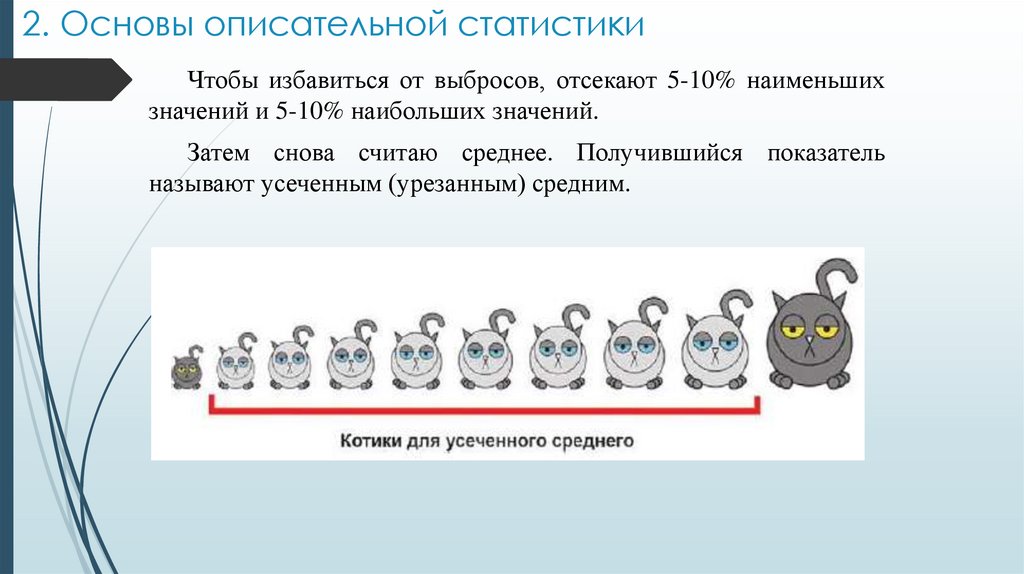
2. Основы описательной статистики
Чтобы избавиться от выбросов, отсекают 5-10% наименьших
значений и 5-10% наибольших значений.
Затем снова считаю среднее. Получившийся показатель
называют усеченным (урезанным) средним.

11.

2. Основы описательной статистики
Меры центральной тенденции:
мода,
медиана,
среднее значение.
Это меры типичности.
Меры изменчивости признака:
размах,
дисперсия,
стандартное отклонение.

12.

2. Основы описательной статистики
Размах – разность между самым большим и самым маленьким
значением признака.
Чтобы избежать искажений, используют межквартильный
размах (предварительно отсекая 25% самых больших значений и
признака и 25% самых маленьких).

13.

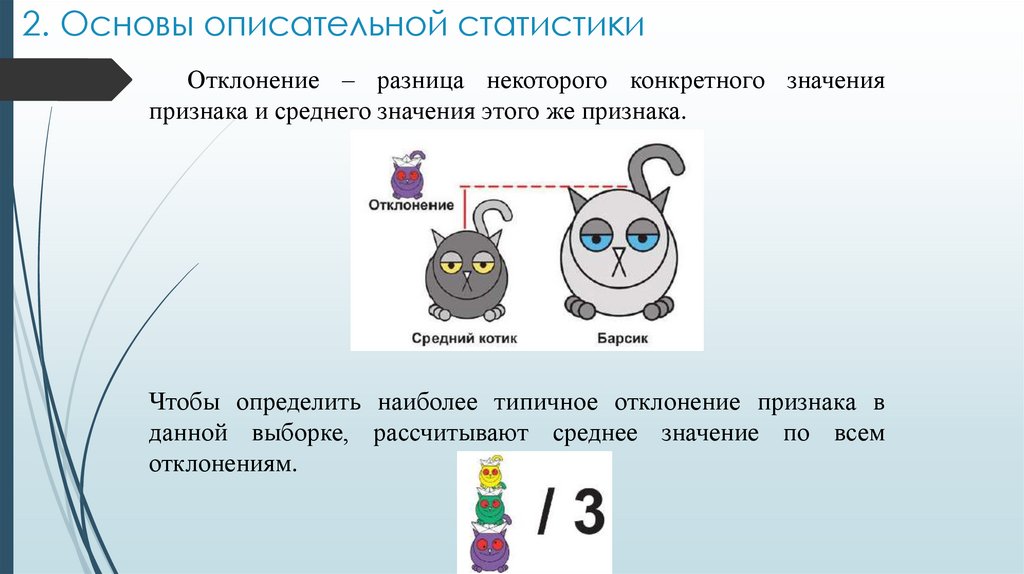
2. Основы описательной статистики
Отклонение – разница некоторого конкретного значения
признака и среднего значения этого же признака.
Чтобы определить наиболее типичное отклонение признака в
данной выборке, рассчитывают среднее значение по всем
отклонениям.

14.

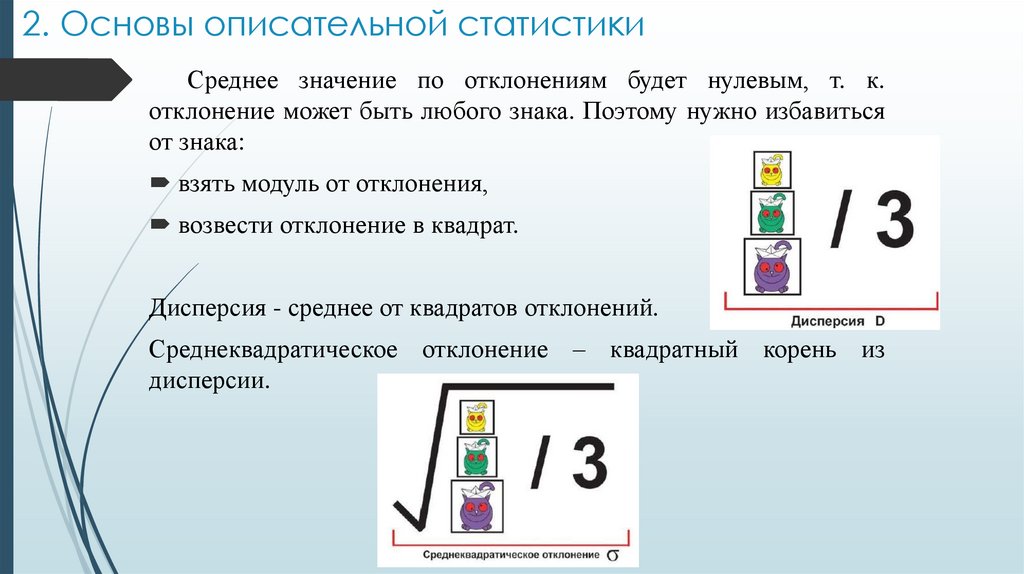
2. Основы описательной статистики
Среднее значение по отклонениям будет нулевым, т. к.
отклонение может быть любого знака. Поэтому нужно избавиться
от знака:
взять модуль от отклонения,
возвести отклонение в квадрат.
Дисперсия - среднее от квадратов отклонений.
Среднеквадратическое отклонение – квадратный корень из
дисперсии.

15.

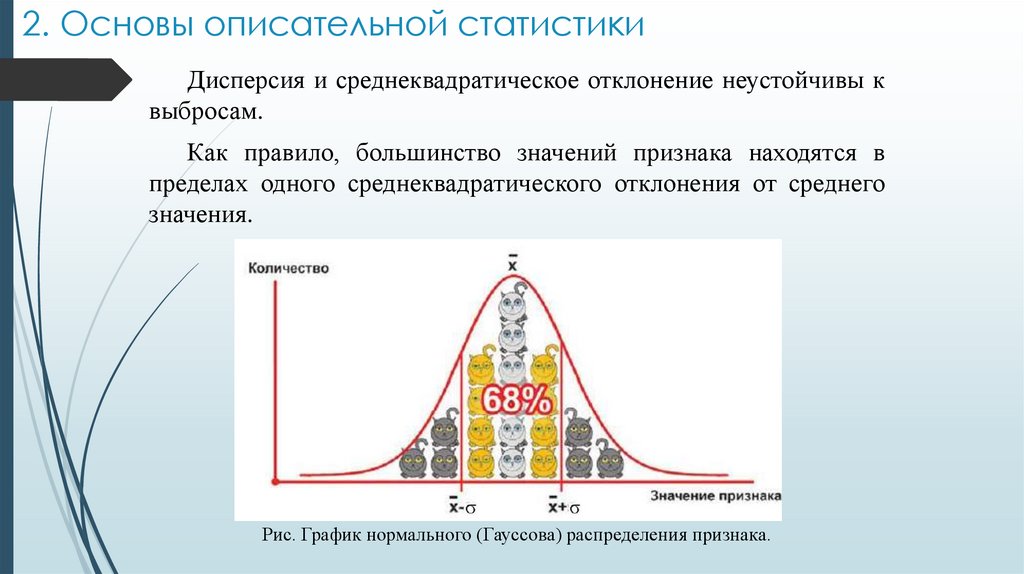
2. Основы описательной статистики
Дисперсия и среднеквадратическое отклонение неустойчивы к
выбросам.
Как правило, большинство значений признака находятся в
пределах одного среднеквадратического отклонения от среднего
значения.
Рис. График нормального (Гауссова) распределения признака.

16.

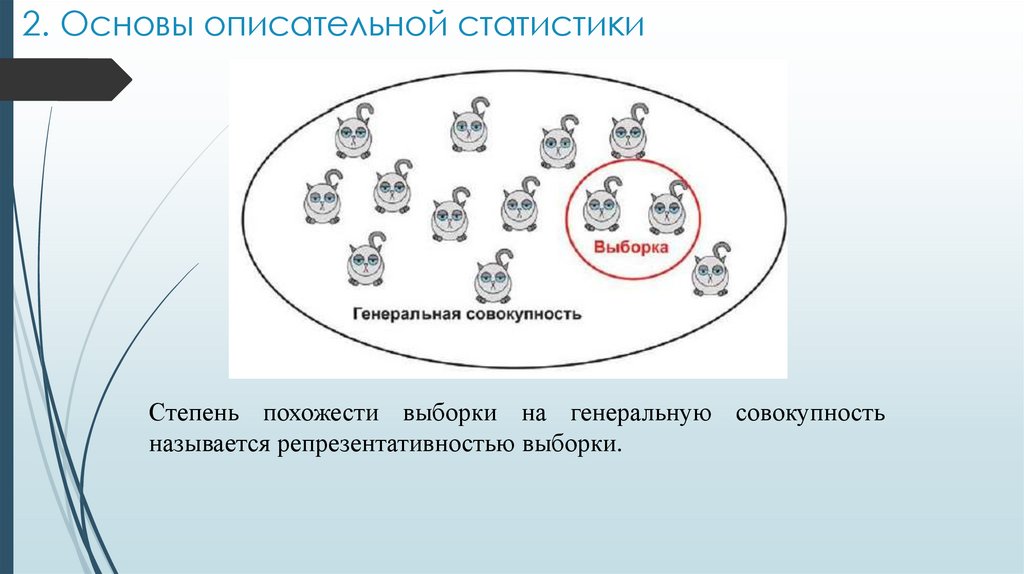
2. Основы описательной статистики
Степень похожести выборки на генеральную совокупность
называется репрезентативностью выборки.

17.

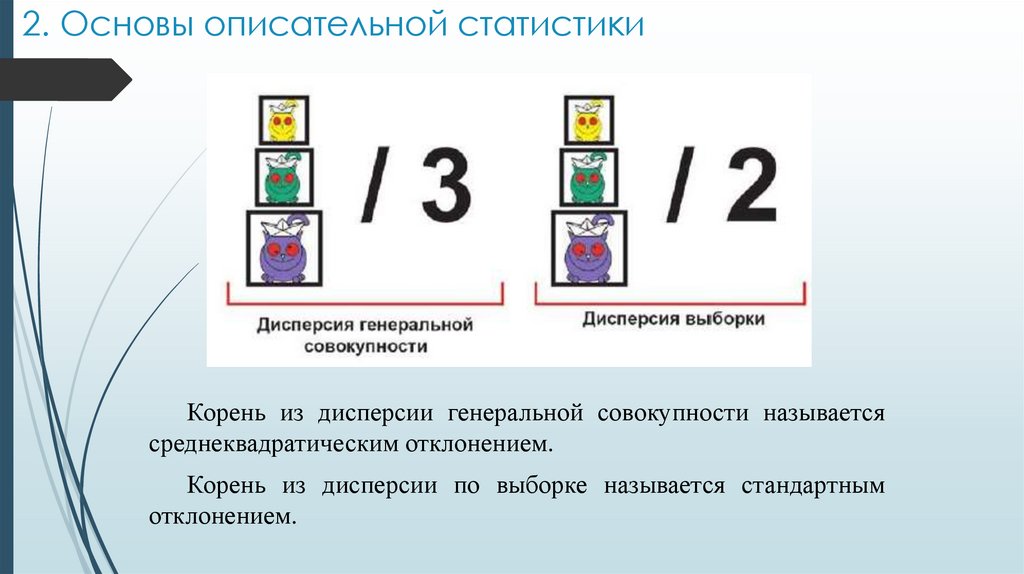
2. Основы описательной статистики
Корень из дисперсии генеральной совокупности называется
среднеквадратическим отклонением.
Корень из дисперсии по выборке называется стандартным
отклонением.

18.

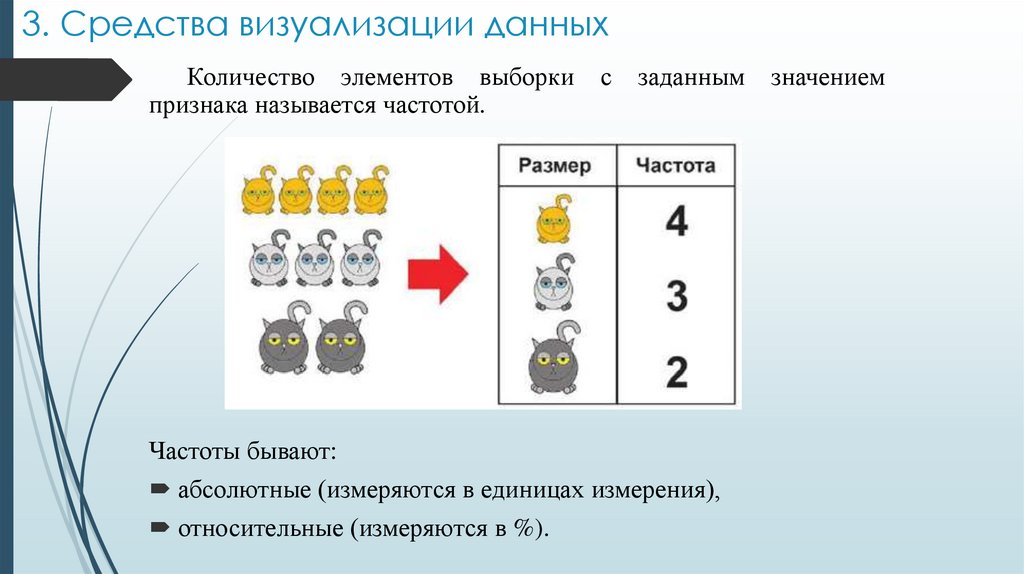
3. Средства визуализации данных
Количество элементов выборки
признака называется частотой.
с
заданным
Частоты бывают:
абсолютные (измеряются в единицах измерения),
относительные (измеряются в %).
значением

19.

3. Средства визуализации данных
Способы визуализации данных, отраженных в таблице частот:
Столбиковая диаграмма
Полигон распределения
Круговая диаграмма

20.

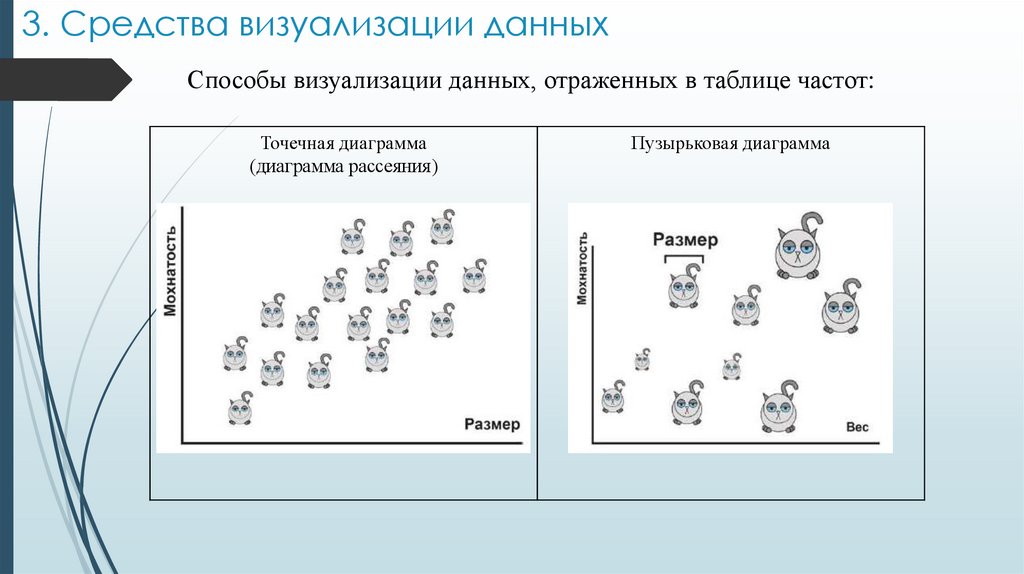
3. Средства визуализации данных
Способы визуализации данных, отраженных в таблице частот:
Точечная диаграмма
(диаграмма рассеяния)
Пузырьковая диаграмма

21.

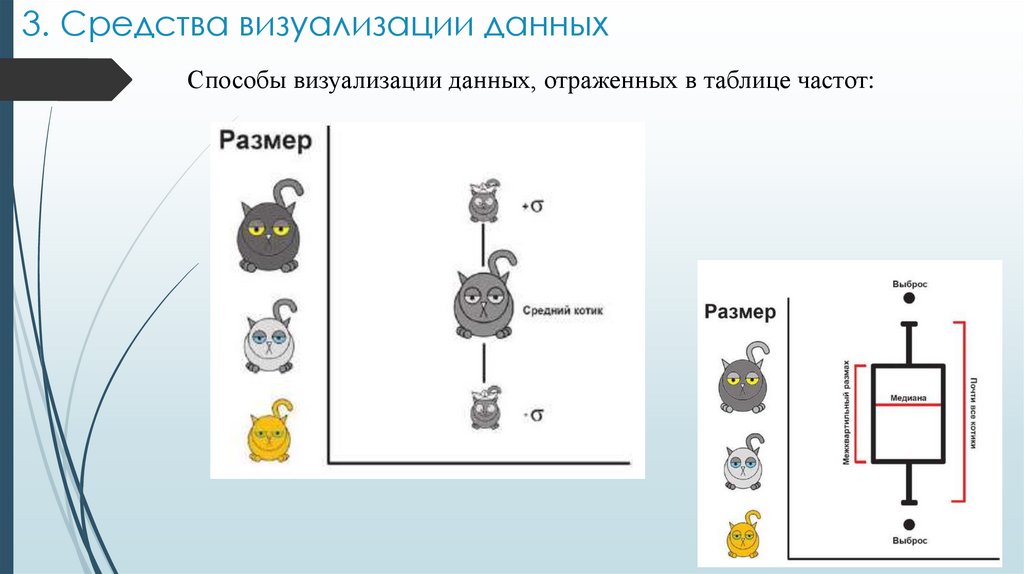
3. Средства визуализации данных
Способы визуализации данных, отраженных в таблице частот:

22.

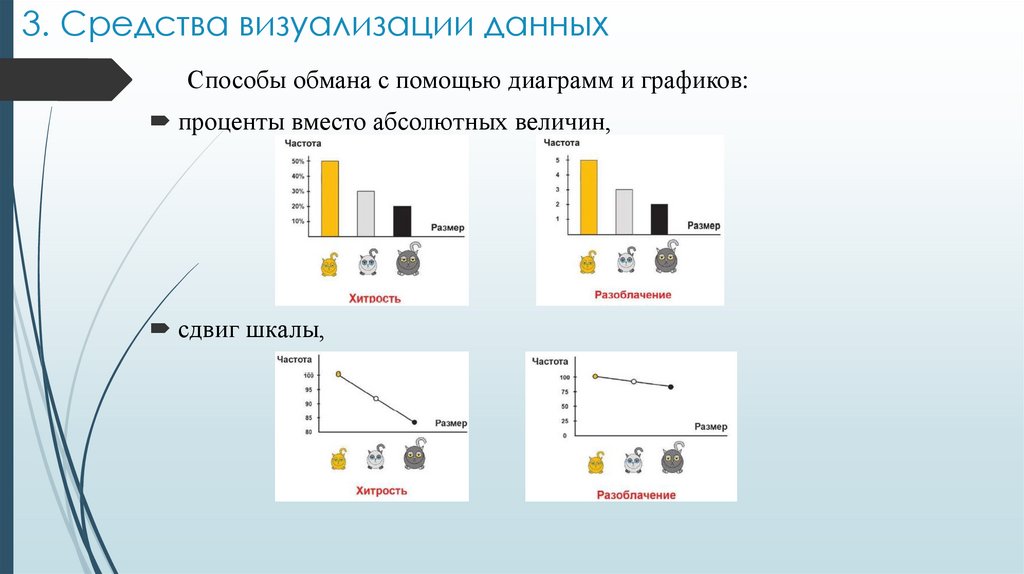
3. Средства визуализации данных
Способы обмана с помощью диаграмм и графиков:
проценты вместо абсолютных величин,
сдвиг шкалы,

23.

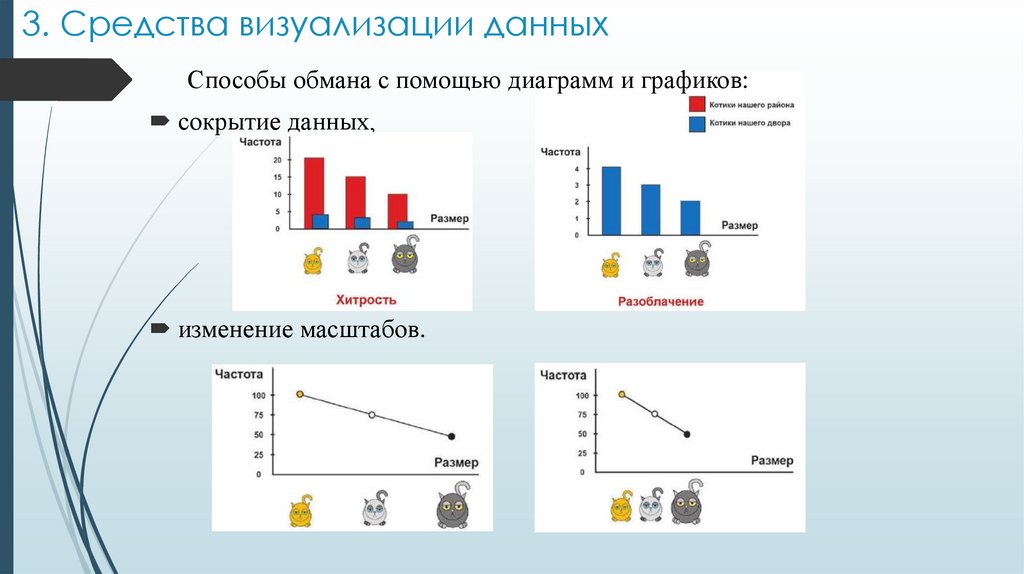
3. Средства визуализации данных
Способы обмана с помощью диаграмм и графиков:
сокрытие данных,
изменение масштабов.

24.

4. Меры различия для несвязанных выборок
Большая часть мер различий для несвязанных выборок
показывает, насколько типичный элемент одной выборки
отличается от типичного элемента другой выборки.

25.

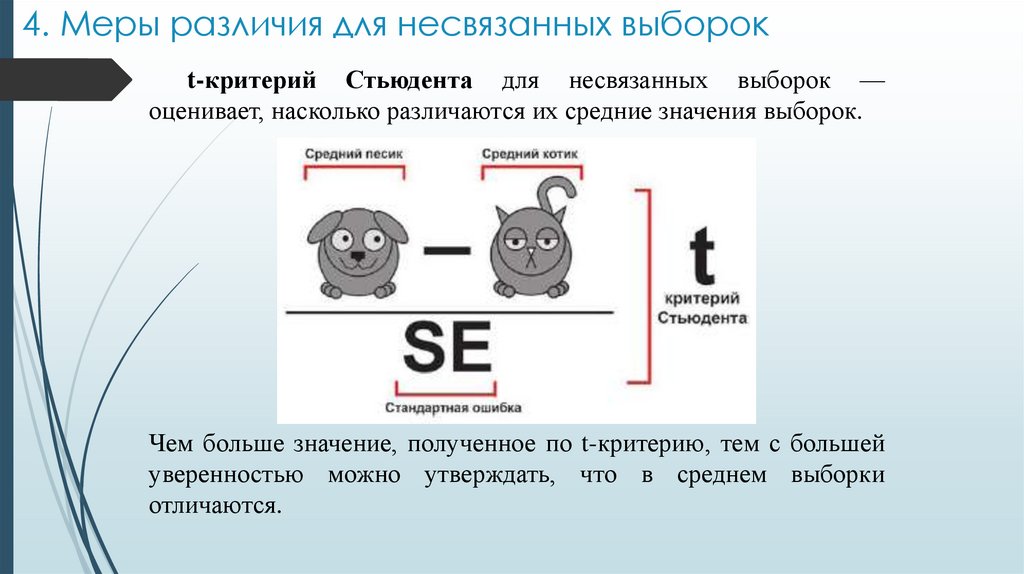
4. Меры различия для несвязанных выборок
t-критерий Стьюдента для несвязанных выборок —
оценивает, насколько различаются их средние значения выборок.
Чем больше значение, полученное по t-критерию, тем с большей
уверенностью можно утверждать, что в среднем выборки
отличаются.

26.

4. Меры различия для несвязанных выборок
Чтобы рассчитать U-критерий Манна-Уитни, необходимо:
выстроить элементы обеих выборок от наименьшего значения
признака к наибольшему и назначить им ранги,
восстановить выборки и посчитать суммы рангов отдельно для
каждой выборки.
Чем больше различаться эти суммы, тем сильнее различаются
выборки.

27.

4. Меры различия для несвязанных выборок
F-критерий равенства дисперсий Фишера
насколько различаются значения признака в выборке.
указывает,
В формуле сверху всегда должна стоять большая дисперсия, а
снизу — меньшая.

28.

4. Меры различия для несвязанных выборок
Когда неизвестны средние значения
используется критерий Хи-квадрат Пирсона:
двух
выборок,
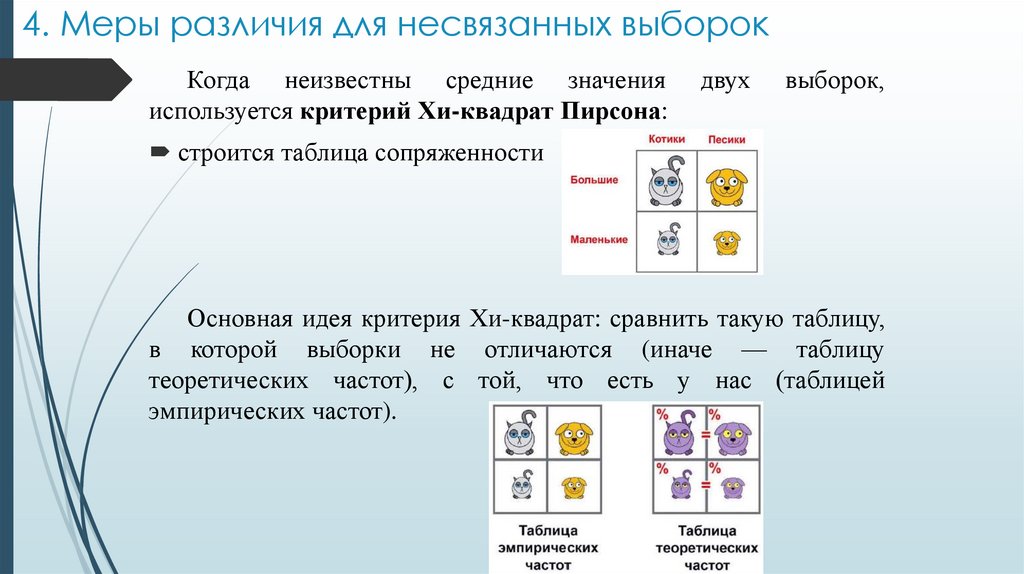
строится таблица сопряженности
Основная идея критерия Хи-квадрат: сравнить такую таблицу,
в которой выборки не отличаются (иначе — таблицу
теоретических частот), с той, что есть у нас (таблицей
эмпирических частот).

29.

4. Меры различия для несвязанных выборок
Когда неизвестны средние значения
используется критерий Хи-квадрат Пирсона:
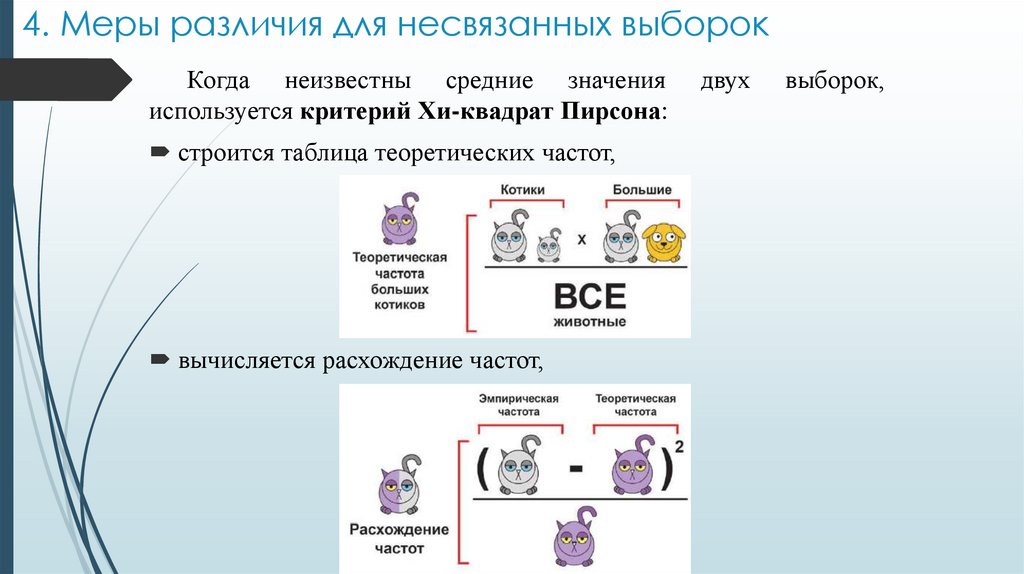
строится таблица теоретических частот,
вычисляется расхождение частот,
двух
выборок,

30.

4. Меры различия для несвязанных выборок
Когда неизвестны средние значения
используется критерий Хи-квадрат Пирсона:
двух
выборок,
складываем получившиеся значения.
Чем больше получившееся значение, тем сильнее отличаются
выборки.

31.

5. Уровень значимости критерия.
Нулевая гипотеза: выборки не отличаются.
Далее вычисляется p-уровень значимости:
вероятность того, что две случайно выбранные группы (выборки)
дадут значение критерия большее или равное тому, которое мы
получили (чаще всего без учета его знака).
Если p-уровень значимости меньше 5%, то нулевая гипотеза
отвергается и принимается альтернативная гипотеза.

32.

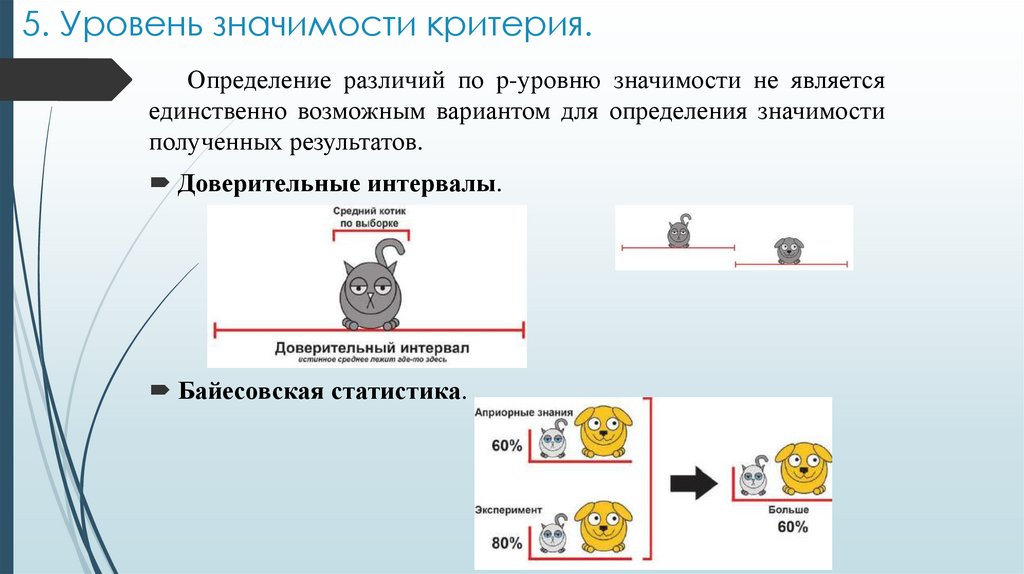
5. Уровень значимости критерия.
Определение различий по p-уровню значимости не является
единственно возможным вариантом для определения значимости
полученных результатов.
Доверительные интервалы.
Байесовская статистика.

33.

6. Статистический анализ текстов
В основе существующих алгоритмов извлечения терминов из
текста лежат статистические или лингвистические методы.
Статистические методы позволяют определить степень
важности слова или словосочетания на основании определенных
числовых закономерностей. Эти методы универсальны.
Лингвистические методы предполагают отбор по некоторым
шаблонам, определенным для предметной области. Эти методы
ограничены конкретным языком, но учитывают его специфику.
Учитывать особенности
семантические методы.
предметной
области
позволяют

34.

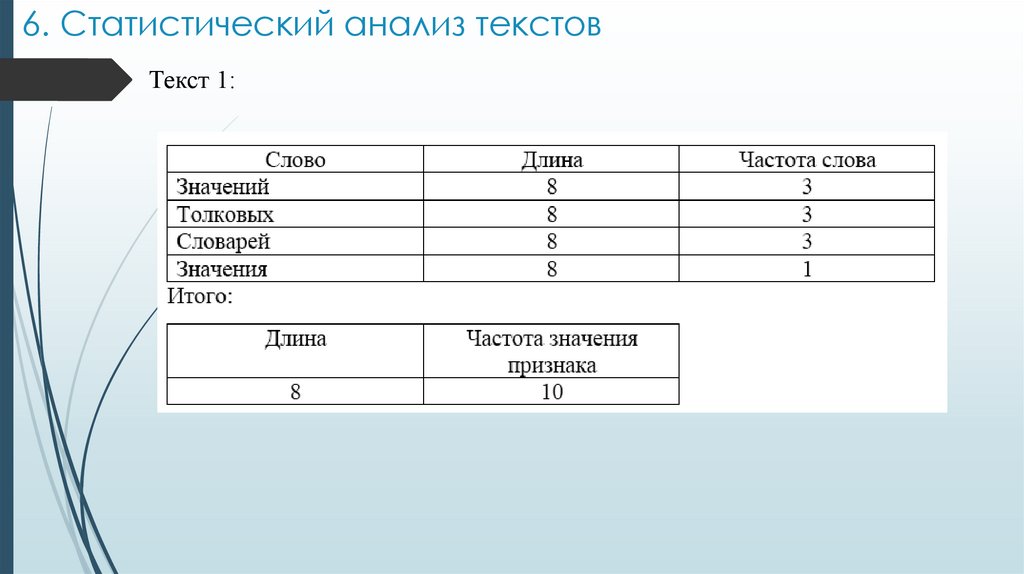
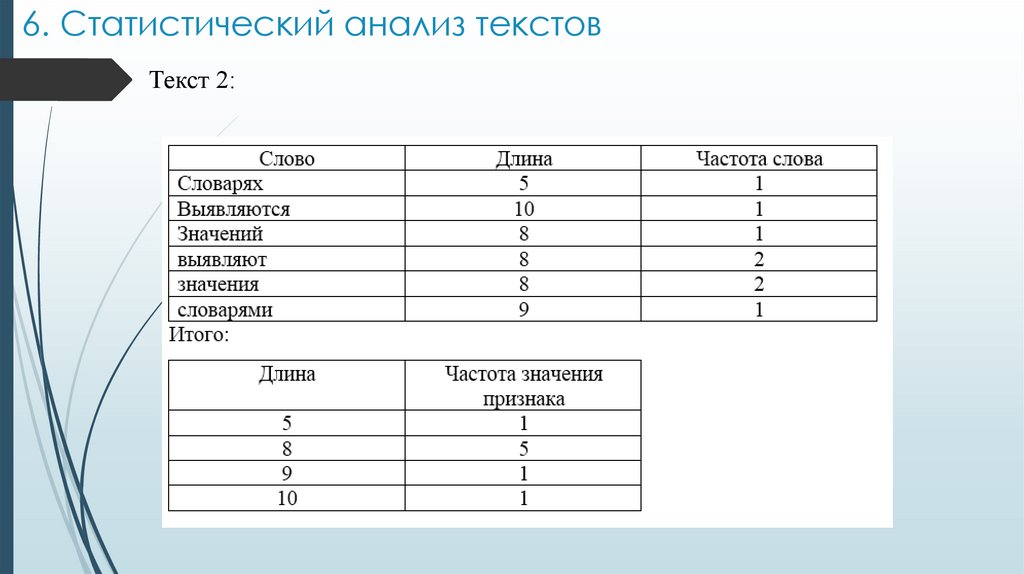
6. Статистический анализ текстов
Рассмотрим некоторые статистические методы работы с
терминами текстов.
Статистический метод подсчета частот
– это метод прямого подсчета частоты n-словий. Результатом его
работы является множество пар «n-словие-его частота».
В основе метода лежит предположение, что высокочастотные
n-словия являются значимыми понятиями.

35.

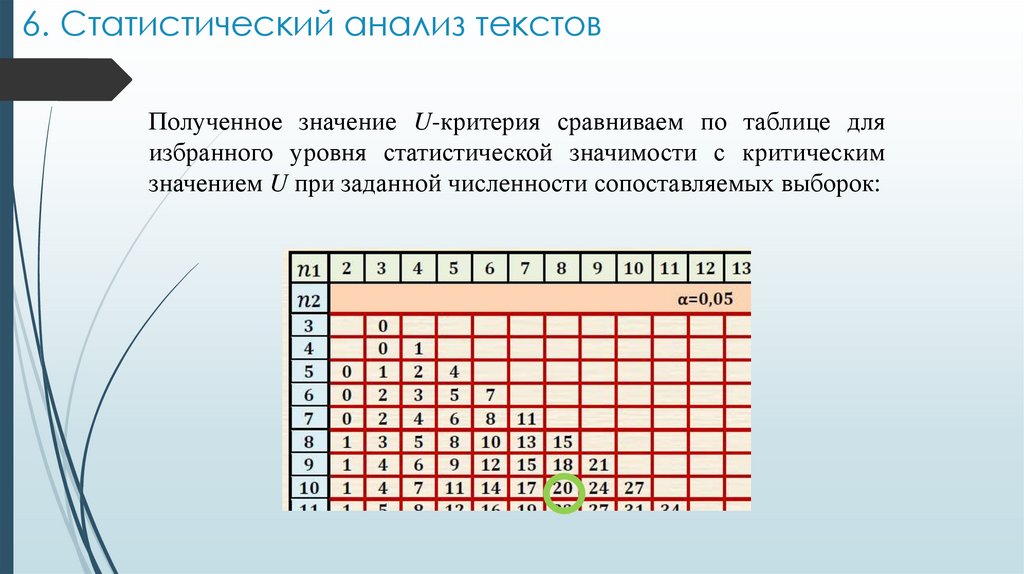
6. Статистический анализ текстов
Статистический метод Mutual Information
применяется только к двусловиям и предполагает вычисление
коэффициента взаимной информации MI на основе частоты
биграммы f(x,y), частот f(x), f(y) каждого слова биграммы в
отдельности и общего количества слов в тексте N: