Комбинаторика

1. КОМБИНАТОРИКА Белокурова Елена Викторовна Доцент, к.э.н.

2.

Дискретная математика – область математики,
изучающая
дискретные
математические
объекты и структуры. Ее элементы возникли в
глубокой древности. С незапамятных времен
известны комбинаторно-логические задачи,
решение которых связано с перебором
комбинаций
дискретных
объектов
и
логическим
анализом
возникающих
вариантов.

3.

Выбор дискретной математики как составляющей при
обучении
математике
вызван
широким
распространением
дискретных
математических
моделей при исследовании кибернетических систем,
повсеместным изучением информатики, теоретической
базой которой является дискретная математика. Кроме
того, целью изучения дискретной математики является
повышение с ее помощью интеллектуального развития
человека, умственное совершенствование обучаемых,
формирование у них приемов логического мышления,
развитие
их
соображения
и
воображения,
формирование
их
личности.

4.

Основными задачами обучения дискретной
математике является развитие логических и
математических способностей обучаемых,
формирование умений построения и анализа
математических моделей и алгоритмов их
исследования, формирование представлений
о математике как едином целом, осознание
связи
между
математикой
и
другими
дисциплинами, связи между математикой и
информатикой.
.

5.

Дискретная математика появилась в учебных планах
специальности «Прикладная математика» в 1974 г. При
обучении дискретной математике студентов вузов
следует обозначить следующую конкретную цель и
задачи: 1) цель - подготовка специалистов высокой
квалификации для продуктивной работы в науке,
образовании, экономике, на производстве; 2) задачи обучение
анализу
реальных
производственных
ситуаций, возникающих в отрасли, построению их
математических моделей и исследованию полученных
моделей с помощью построенных алгоритмов или
пакетов прикладных программ.

6.

Целью изучения дисциплины «Дискретная математика»
является прочное усвоение студентами (школьниками)
теоретических и практических основ дискретной
математики, математической логики, комбинаторики и
теории
графов,
составляющих
фундамент
ряда
математических,
компьютерных
дисциплин
и
дисциплин
прикладного
характера.
Задачами изучения данной дисциплины являются:
обучение
студентов
(школьникам)
теоретическим
основам
курса,
овладение
методами
решения
практических
задач,
приобретение
навыков
самостоятельной научной деятельности.

7.

За последние десятилетия произошло значительное
усиление роли дискретной математики в решении
практических задач и интенсивное использование
информатики, теоретической базой которой является
дискретная математика, в науке, технике, экономике и
повседневной жизни. Все это во многом связано с
изучением
кибернетических
систем,
получивших
весьма широкое распространение, при моделировании
которых
существенно
используется
дискретная
математика. В последнее время их изучение стало
более актуальным в связи с увеличением масштабов
производства, расширением экономических связей,
созданием
межгосударственных
объединений.

8.

Широкое распространение ЭВМ вызвало изучение
программирования и информатики, непосредственно
связанной с дискретной математикой, практически во
всех
учебных
заведениях.
Использование
для
исследования сложных объектов и ситуаций моделей
дискретной математики требует глубокого ознакомления
с
методикой
их
построения,
изучения
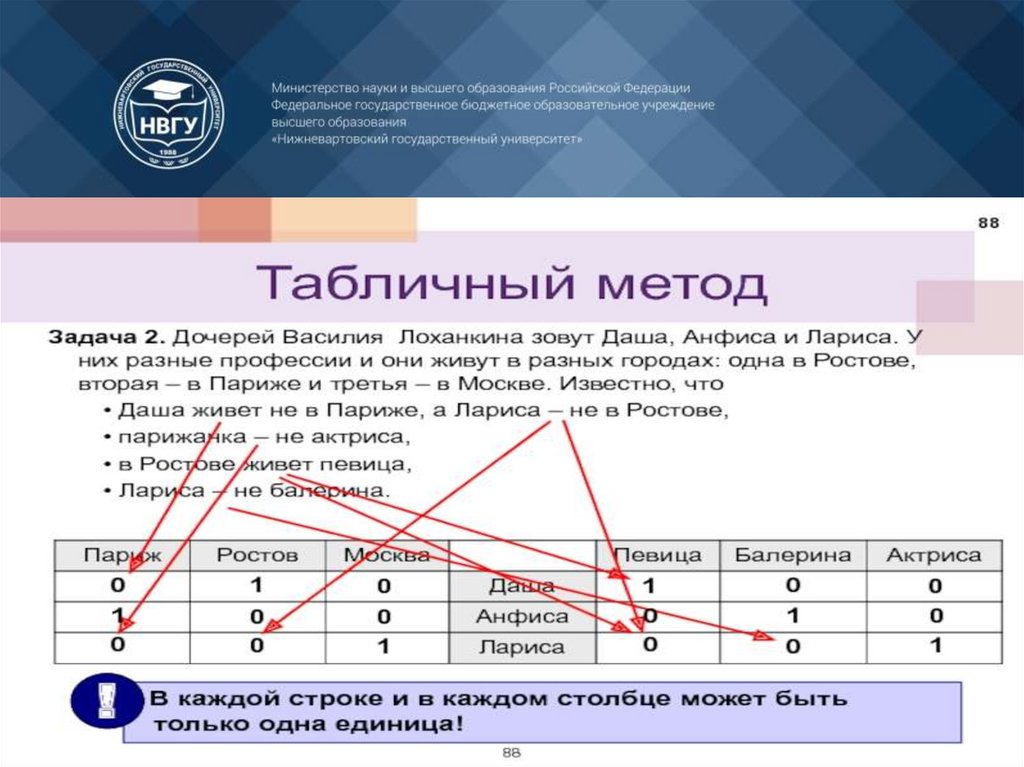
методов
дискретной математики и способов ее применения для
решения практических задач студентами естественных,
технических и экономических специальностей.

9.

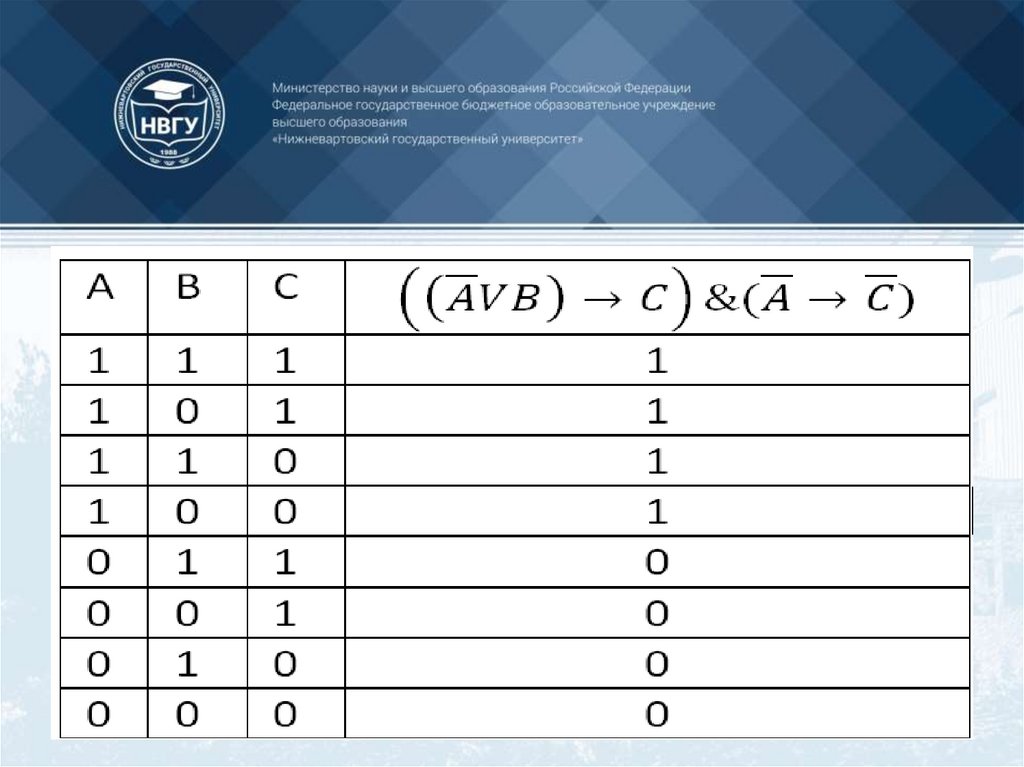
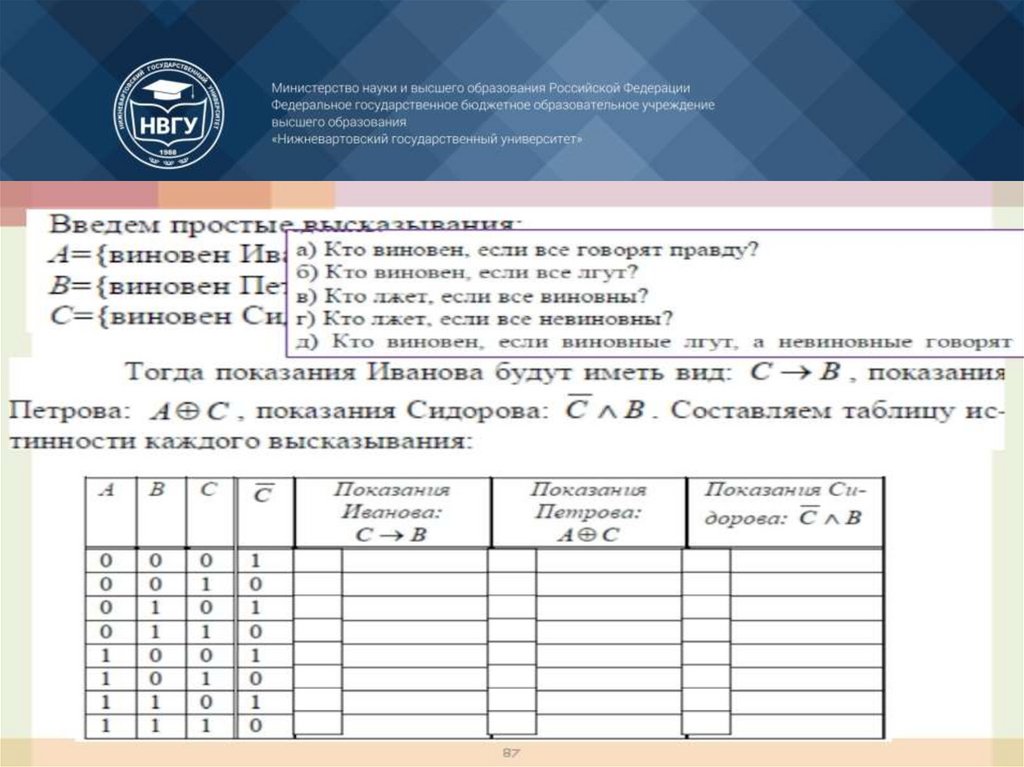
При этом необходимо обучение студентов умениям
создания эффективных алгоритмов исследования
моделей, оценивания их качества и скорости,
сравнения алгоритмов с ранее существующими. Кроме
того, большое значение приобретает умение будущих
специалистов исследовать построенные модели на
компьютерах
с
помощью
пакетов
прикладных
программ.
Поэтому
становится
важным
раннее
пропедевтическое
ознакомление
с
началами
дискретной математики, начиная с дошкольных
заведений и школы, и заканчивая в вузе.

10.

Решение задач дискретной математики на начальном
уровне ее изучения не требует глубоких теоретических
знаний, а нуждается только в сообразительности,
поэтому их можно широко использовать для ускорения
математического развития школьников. Часто такие
задачи легко представить в занимательной форме, что
способствует повышению интереса к обучению. Кроме
того, дискретную математику можно использовать для
решения
методических
задач
в
математическом
образовании. Например, с ее помощью возможно
знакомство школьников с математической индукцией,
тяжелыми
для
них
понятиями
«необходимые
и
достаточные условия» и т.д.

11.

Комбинаторика - раздел математики, который изучает
задачи выбора и расположения элементов из
некоторого основного множества в соответствии с
заданными
правилами.
Формулы
и
принципы
комбинаторики используются в теории вероятностей
для подсчета вероятности случайных событий и,
соответственно, получения законов распределения
случайных величин. Это, в свою очередь, позволяет
исследовать закономерности массовых случайных
явлений,
что
является
весьма
важным
для
правильного
понимания
статистических
закономерностей,
проявляющихся
в
природе
и
технике.

12.

1. ОСНОВНЫЕ ПОНЯТИЯ
Комбинаторику можно рассматривать как
часть теории множеств, так как любую
комбинаторную задачу можно свести к
задаче о конечных множествах и их
отображениях.
Центральная
задача
комбинаторики - задача о размещении
объектов в соответствии со специальными
правилами.

13.

В комбинаторике нам дана совокупность n
элементов (n - множество или генеральная
совокупность объема n), из которой мы будем
в соответствии с определенными правилами
выбирать часть этой совокупности (m подмножество, n- множества или выборку
объема m). Для доказательства основных
формул
комбинаторики
достаточно
применить принцип математической индукции
и правила сложения и умножения.

14.

1.1. Элементы теории множеств
Напомним, что под множеством понимают
совокупность
элементов
произвольной
природы,
рассматриваемую
как
единое
целое. Множества обычно обозначаются
заглавными буквами A, В, С.

15.

Конечные
множества
обычно
задаются
перечислением
своих
элементов
или
свойством: L = {а, b, с, d, e, f, g, h, i, j, k, l, m, n,
o, p, q, r, s, t, u, v, w, x, у, z} - множество букв
латинского алфавита; F = {0, 1, 2, 3, 4, 5, 6, 7,
8, 9) – множество цифр; В = {Ц, Г } —
множество исходов опыта, заключающегося
в
подбрасывании
монеты
один
раз,
определяется своими элементами Ц (монета
падает цифрой вверх) и Г (монета падает
гербом вверх).

16.

Определение.
Если
каждый
элемент
множества X является в то же время
элементом множества У, то говорят, что X часть или подмножество множества У: X У.
Множество A = {0, 2, 4, 6, 8} четных чисел
является частью множества B = {0, 1, 2, 3, 4, 5,
6, 7, 8, 9} всех цифр.

17.

Определение. Пересечением множеств X и У
называется множество Х ∩ У, состоящее из
элементов, которые принадлежат как X, так и
У.
Пересечением множества A = {0, 2, 4, 6, 8}
четных цифр и множества В = {1, 3, 5, 7, 9}
нечетных цифр является пустое множество
A ∩ B =Ø.
Если A = {1,2,3} и В = {2,3,4}, то
A ∩ В = {2,3}.

18.

Определение. Объединением множеств X и У
называют множество X
У, состоящее из
элементов, которые принадлежат хотя бы
одному из множеств X, У.
Объединением множества A = {0, 2, 4, 6, 8}
четных цифр и множества B = {1, 3, 5, 7, 9}
нечетных цифр является множество
A
B={0,1,2,3,4,5,6,7,8,9} всех цифр.
Если A = {1,2,3} и B = {2,3,4}, то A B ={1,2, 3,4}.

19.

Для конечного множества A через n(А)
обозначим число его элементов. Число
элементов пустого множества, очевидно,
равно
нулю
n(Ø)=0.
Число
элементов
множества
A
=
{а},
образованного
единственным элементом a, равно единице,
n(А) = 1.
Число элементов множества F = {0, 1, 2, 3, 4,
5, 6, 7, 8, 9}, составленного из цифр, равно
десяти: n(F) = 10.

20.

Теорема
1.
Если пересечение конечных
множеств A и B пусто, то число элементов в их
объединении равно сумме чисел элементов
множеств A и B, т.е. если A ∩ B = Ø → n (А В) =
n (А) + n (В).
Это правило легко распространить на любое
конечное число множеств.

21.

Определение. Два любых элемента а и b
представляют собой упорядоченную пару,
если предварительно оговорено, какой из
них считается первым, а какой - вторым
(a, b).

22.

Определение.
Декартовым
произведением
множеств A и В называется множество всех
тех упорядоченных пар, в которых первый член
является элементом А, а второй – элементом В:
(А · В)
А = {a, l, i}, n (А) = 3,
В={b, с}, n (В) = 2,
А · В = {(а, b), (а, с), (l, b), (l, с), (i, b), (i, с)},
n (А · В) = 6, В · В = {(b, b), (b, с), (с, b), (с, с)},
n (В · В) = 4.

23.

Теорема 2. Если множества A и В конечны, то
число пар в их декартовом произведении
А · В равно произведению чисел элементов
этих множеств: n (А · В) = n (А) · n (В)
A = {1, 2, 3}, n (А) = 3
В ={4, 5,6}, n (В) = 3
А · В = {14, 15, 16, 24, 25,26, 34,35, 36},
n (А · В) = n (А) · n (В) = 3 · 3 = 9.
Применяя метод математической индукции,
это правило легко распространить на любое
конечное число множеств.

24.

1.2. Правила сложения и умножения в
комбинаторике
Из теорем 1-2 следуют два простых правила
комбинаторики

25.

Правило суммы. Если два действия взаимно
исключают друг друга, причем одно из них
можно выполнить m способами, а другое – n
способами, то выполнить одно любое из
этих действий можно n + m способами.

26.

Правило
умножения.
Пусть
требуется
выполнить последовательно k действий. Если
первое действие можно выполнить 1 n
способами, второе действие 2 n способами,
третье - 3 n способами и так до k-го действия,
которое можно выполнить k n способами, то
все k действий вместе могут быть выполнены
N = n1 · n2 · n3 · … · nк способами.
Эти правила дают удобный универсальный
метод решения многих задач.

27.

Задача 1.
В группе 30 человек. Необходимо
выбрать
старосту
и
профорга.
Сколькими способами можно это
сделать?

28.

Решение.
Старостой может быть выбран любой из 30
учащихся, то есть существует 30 способов
выбора старосты. После того, как староста
уже выбран, профоргом можно выбрать
любого из оставшихся 29 учащихся. Согласно
правилу умножения, общее число способов
выбора старосты и профорга равно 30 · 29 =
870.

29.

Задача 2.
Необходимо составить варианты контрольной
работы,
каждый
из
которых
должен
содержать
три
задачи.
Первая
задача
выбирается из любого параграфа I главы
сборника, вторая - из любого параграфа II
главы, а третья - из любого параграфа III
главы. Сколько видов контрольной работы
можно составить, если I и III глава содержат
два параграфа, а II глава - три параграфа?

30.

Решение.
Нужно найти число способов выбора трех задач из трех
соответствующих глав. Первую задачу можно выбрать
двумя способами, так как I глава содержит 2 параграфа.
Вторую задачу можно выбрать тремя способами, так как
II глава содержит 3 параграфа. Третью задачу можно
выбрать двумя способами, так как III глава содержит 2
параграфа. Общее число способов выбора трех задач по
теореме умножения равно 2·3·2 = 12. Таким образом,
можно составить 12 различных видов контрольной
работы.

31.

Решение.
Первый мальчик может сесть на любое из
четырех четных мест, второй - на любое из
оставшихся трех мест, третий - на любое из
оставшихся двух мест. Последнему мальчику
предоставляется всего одна возможность.
Согласно правилу умножения мальчики могут
занять четыре места 4·3·2·1 = 24 способами.
Столько же возможностей имеют и девочки.
Таким образом, согласно правилу умножения,
мальчики и девочки могут занять все стулья
24·24 = 576 способами.

32.

Задача 4.
Имеется 20 изделий 1-го сорта и 30 изделий
2-го сорта. Необходимо выбрать 2 изделия
одного сорта. Сколькими способами можно
это сделать?

33.

Решение.
Согласно условию задачи следует выбрать 2
изделия одного сорта, неважно какого. Это
могут быть либо изделия 1-го сорта, либо
изделия 2-го сорта. По правилу умножения два
изделия 1-го сорта можно выбрать 20·19 = 380
способами. Аналогично два изделия 2-го сорта
можно выбрать 30·29 = 870 способами. Выбор 2
изделий 1-го сорта исключает выбор 2 изделий
2-го сорта. Тогда по правилу 9 сложения общее
число способов выбора изделий одного сорта
равно 380 + 870 = 1250.

34.

Мы рассмотрели некоторые общие правила
решения комбинаторных задач. С их помощью
можно решать задачи самых разных типов.
Однако, как в геометрии неудобно всегда
сводить решение задачи к аксиомам, а
удобнее пользоваться теоремами, так и в
комбинаторике вместо решения задачи по
общим правилам часто удобнее пользоваться
готовыми формулами для некоторых типов
задач, которые встречаются чаще других.

35.

2. ОСНОВНЫЕ ФОРМУЛЫ
КОМБИНАТОРИКИ.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

36.

2.1. Выборки
Рассмотрим множество A = { a1 , a2 ,…, an },
содержащее n различных элементов, которое
будем
называть
n-множеством
или
генеральной совокупностью объема n.
Из n-множества можно образовать его части
(подмножества).

37.

Определение. Подмножество, состоящее из m
элементов n-множества, называют
m-подмножеством
n-множества
или
соединением из n элементов по m, или
выборкой
объема
m
из
генеральной
совокупности объема n.

38.

Возможны два способа выбора: 1. Выбор без
возвращения, при котором однажды выбранный
элемент
удаляется
из
генеральной
совокупности. Выборка (соединение) в этом
случае не содержит повторяющихся элементов.
2. Выбор с возвращением, при котором выбор
производится каждый раз из всей генеральной
совокупности, то есть перед следующим
выбором предыдущий выбранный элемент
возвращается в генеральную совокупность. В
выборке
(соединении)
в
этом
случае
встречаются повторения.

39.

Какие выборки одного и того же объема считать
различными и какие одинаковыми, зависит от правил
выбора соединения (подмножества, выборки).
Два соединения могут отличаться либо 1) составом, если
они содержат хотя бы по одному различному элементу,
либо 2) порядком входящих элементов.
В зависимости от правил выбора соединения делят на
три типа: размещения, перестановки, сочетания. В
зависимости от способа выбора (без возвращения или с
возвращением) каждый тип соединения может быть без
повторений или с повторениями.

40.

2.2. Размещения с повторениями
Классической задачей комбинаторики является задача
о числе размещений без повторений, содержание
которой
можно
выразить
вопросом:
сколькими
способами можно выбрать и разместить по m
различным местам m из n различных предметов?
Также классической задачей комбинаторики является
задача
о
числе
размещений
с
повторениями,
содержание
которой
можно
выразить
вопросом:
сколькими способами можно выбрать и разместить по
m различным местам m из n предметов, среди которых
есть одинаковые?

41.

Определение. Размещениями из n элементов по m
называются соединения из n элементов по m, которые
отличаются друг от друга либо своими элементами
(составом), либо порядком их расположения. На языке
теории множеств это звучит следующим образом:
размещения из n элементов по m - это упорядоченное
m -подмножество n-множества (упорядоченная m выборка из генеральной совокупности
объема n).
Термин «упорядоченная» означает, что порядок
следования
элементов
в
выборке
существенен:
выборки с одними и теми же элементами, но с разным
порядком их следования различны.

42.

Задача.
Пусть имеется множество, содержащее 4
буквы: {А, В, С, D}. Записать все возможные
размещения из 4 указанных букв по две:
а) без повторений;
б) с повторениями.

43.

Решение.
а) Таких размещений 12: (АВ), (AC), (AD), (ВС),
(BD), (ВА), (СА), (CB), (CD), (DA), (DB), (DC).
Заметим,
что
размещения
отличаются
порядком входящих в них элементов и их
составом. Размещения АВ и ВА содержат
одинаковые
буквы,
но
порядок
их
расположения различен.
б) Таких размещений 16. К приведенным для
случая
(а)
размещениям
добавляются
размещения из одинаковых элементов (АА),
(BB), (CC), (DD).

44.

Задача.
Пусть имеется множество, содержащее 2
буквы {А, B}. Записать все возможные
размещения с повторениями из 4-х букв

45.

Решение.
Таких размещений 16: (АААА), (ВВВВ), (АААВ),
(ААВА), (АВАА), (ВААА), (ААВВ), (АВАВ), (ВАВА),
(ВВАА), (АВВА), (ВААВ), (ВВВА), (ВВАВ), (ВАВВ),
(АВВВ).

46.

Теорема 3. Число
различных размещений без
m
повторений An из n элементов по m равно
n!
An n m !
m
для выборки без возвращения.
(1)

47.

Число размещений с повторениями
элементов по m равно
An n
m
m
для выборки с возвращением.
A
m
n
из n
(2)

48.

Задача.
В некоторой газете 12 страниц. Необходимо
на страницах этой газеты поместить четыре
фотографии. Сколькими способами можно
это сделать, если ни одна страница газеты не
должна содержать более одной фотографии?

49.

Решение.
В данной задаче генеральной совокупностью являются
12 страниц газеты, и выборкой без возвращения 4
выбранные из них страницы для фотографий. В данной
задаче важно не только то, какие выбраны страницы,
но и в каком порядке (для расположения фотографий).
Таким образом, задача сводится к классической
задаче об определении числа размещений без
повторений из 12 элементов по 4 элемента:
12!
12! 12 11 10 9 8 7 6 5 4 3 2 1
12 11 10 9 11880
A12 12 4 ! 8!
8 7 6 5 4 3 2 1
4
Таким образом, 4 фотографии
расположить 11880 способами.
на
12
страницах
можно

50.

Задача.
Телефонная книга раскрывается наудачу и
выбирается
случайный
номер
телефона,
который состоит из 7 цифр. Сколько существует
вариантов выбора при условии:
а) все цифры номера различны;
б) все цифры номера могут быть любыми из
имеющихся десяти;
в) четыре последние цифры телефонного
номера одинаковы.

51.

Решение.
а) В данной задаче генеральной совокупностью
является десять цифр {0, 1, 2, 3, 4, 5, 6, 8, 9}. Так как
цифры в номере повторяться не могут, то опыт состоит в
7-кратном выборе без возвращения одной из этих 10
цифр. В номере важен порядок следования цифр.
Следовательно, число вариантов выбора определяется
числом размещений без повторений из 10 цифр по 7:
10!
10! 10 9 8 7 6 5 4 3 2 1
10 9 8 7 6 5 4 604800
A10 10 7 ! 3!
3 2 1
7

52.

б) Опыт состоит в 7-кратном выборе с
возвращением любой цифры из 10. То есть
число вариантов выбора определяется числом
размещений с повторениями из 10 элементов
по 7:
A 10
7
10
7

53.

в) Первые четыре цифры выбираются из
любых десяти с возвращением, а три
последние
цифры
номера
однозначно
определяются
уже выбранной
четвертой
цифрой. Таким обратом, число вариантов
выбора определяется числом размещений с
повторениями из 10 элементов по 4:
4
A
10
10
4

54.

2.3. Перестановки без повторений
Классической
задачей
комбинаторики
является задача о числе перестановок без
повторения, содержание которой можно
выразить вопросом: сколькими способами
можно разместить m различных предметов
на n различных местах?

55.

Определение.
Размещения,
в
которых
участвуют все n элементов генеральной
совокупности,
называются перестановками
без повторений из n элементов. Перестановки
состоят из одних и тех же элементов, но
отличаются между собой порядком.

56.

Задача.
Пусть имеется множество букв {А, В, С}.
Записать все возможные перестановки.
Решение.
Этому множеству букв соответствует 6
перестановок: (ABC), (АСВ), (ВАС), (ВСА),
(СВА), (CAB).

57.

Теорема. Число перестановок n различных
элементов равно n!, т.е.
Pn = n!

58.

Задача.
Сколько можно составить четырехбуквенных
«слов» из букв слова «брак»?
Решение.
Генеральной
совокупностью
являются
4
буквы слова «брак» {б, р, а, к}. Число «слов»
определяется перестановками этих 4 букв, т.е.
P4 = 4! = 1 · 2 · 3 · 4 = 24.

59.

Задача.
Сколькими
способами
можно
расставить
десять
различных книг на полке, чтобы определенные четыре
книги стояли рядом?
Решение.
В исходной генеральной совокупности - 10 разных книг.
Будем считать выделенные 4 книги за одну. Тогда для
остальных 6 книг существует P6 = 6! = 720 перестановок.
Однако четыре определенные книги можно переставить
между собой P4 = 4! = 24 способами. По правилу
умножения имеем P6 · P4 = 720 · 24 =17280.

60.

2.4. Перестановки с повторениями
Для случая, когда среди выбираемых n
элементов есть одинаковые (выборка с
возвращением), задачу о числе перестановок
с повторениями можно выразить вопросом:
сколькими способами можно переставить n
предметов, расположенных на n различных
местах, если среди n предметов имеются k
различных типов (k < n), т. е. есть одинаковые
предметы

61.

Определение. Перестановками с повторениями
называются
соединения
из
генеральной
совокупности, каждое из которых содержит n
элементов, среди которых элемент
a1 повторяется n1 раз,
a2 повторяется n2 раз,
...................
an повторяется nk раз
n1 + n2 + ... + nk = n
и которые отличаются друг от друга только
порядком расположения различных элементов.

62.

Теорема. Число перестановок с повторениями
P (n , n ,...., n )
n
1
2
k
равно
n!
P n(n1, n 2,...., n k ) ! !...... !
n1 n 2 n k

63.

Задача
Сколько разных буквосочетаний можно сделать из
букв слова «Миссисипи»?
Решение.
Здесь 1 буква «м», 4 буквы «и», 3 буквы «с» и 1 буква
«п», всего 9 букв. Следовательно, число перестановок
с повторениями равно
9!
P 9(1, 4, 3,1) 1!4!3!1! 2520

64.

2.5. Сочетания без повторений
Классической
задачей
комбинаторики
является задача о числе сочетаний без
повторений, содержание которой можно
выразить вопросом: сколькими способами
можно выбрать m из n различных предметов?

65.

Определение. Сочетаниями из n различных
элементов по m называются соединения из n
элементов по m (m ≤ n), которые отличаются
друг от друга только составом элементов.

66.

Задача.
Пусть имеется множество, содержащее 4 буквы {А, B, С,
D}. Запишем все возможные сочетания из указанных
букв по 3.
Решение. Таких сочетаний 4: ABC, ACD, ABD, BCD. Здесь
в число сочетаний не включены, например, АСВ, ВСА,
так
как
они
не
отличаются
по
составу
от
последовательности букв ABC, потому что перестановка
элементов нового сочетания не дает.

67.

Теорема. Число сочетаний из n элементов по
m равно
n!
C n m! n m !
m

68.

Задача.
Необходимо выбрать в подарок 4 из 10 имеющихся
различных книг. Сколькими способами можно это
сделать?
Решение.
Генеральной совокупностью является 10 различных
книг. Из них нужно выбрать 4, причем порядок выбора
книг не играет роли. Нужно найти число сочетаний из
10 элементов по 4:
10!
10 9 8 7 6 5 4 3 2 1
C 10 4! 10 4 ! 4 3 2 1 (6 5 4 3 2 1) 210
4

69.

Задача.
Имеется 10 белых и 5 черных шаров.
Сколькими способами можно выбрать 7
шаров, чтобы среди них были 3 черных?

70.

Решение.
Имеем 15 шаров: 10 белых и 5 черных. Нужно выбрать 7
шаров: 4 белых и 3 черных. Разобьем 15 шаров на 2
генеральные совокупности:
1) 10 белых шаров;
2) 5 черных шаров.
4 белых шара будем выбирать из I генеральной совокупности,
порядок выбора безразличен, их можно выбрать
C 10
4
10!
210
4! 10 4 !
способами. 3 черных шара будем выбирать из II генеральной
совокупности, их можно выбрать
5!
C 5 3!2! 10
3
способами.

71.

Тогда по правилу умножения искомое число способов равно
C
4
10
C 5 2100
3

72.

Решение этой задачи можно схематически представить
следующим образом:

73.

Задача.
Десять команд участвуют в розыгрыше
первенства по футболу, лучшие из которых
занимают 1-е, 2-е и 3-е место. Две команды,
занявшие
последние
места,
не
будут
участвовать
в
следующем
таком
же
первенстве.
Сколько
разных
вариантов
результата первенства может быть, если
учитывать только положение первых трех и
последних двух команд.

74.

Решение.
Имеется генеральная совокупность объема 10 команд.
Из нее будем выбирать 5 команд в 2 этапа: 1) сначала
на первые 3 места из 10 с учетом состава и порядка
команд; 2) затем на последние 2 места из оставшихся
7 с учетом только состава (порядок выбывших команд
не важен). Первые 3 места могут быть распределены
A10
3
способами
10!
10!
720
10 3 ! 7!

75.

Число способов исключить 2 команды из оставшихся 7
равно
7!
7!
2
C 7 2 ! 5! 21
7
Согласно правилу умножения получаем, что число
разных результатов неравенства равно
A C 15120
3
2
10
7

76.

Решение этой задачи можно схематически
представить следующим образом:

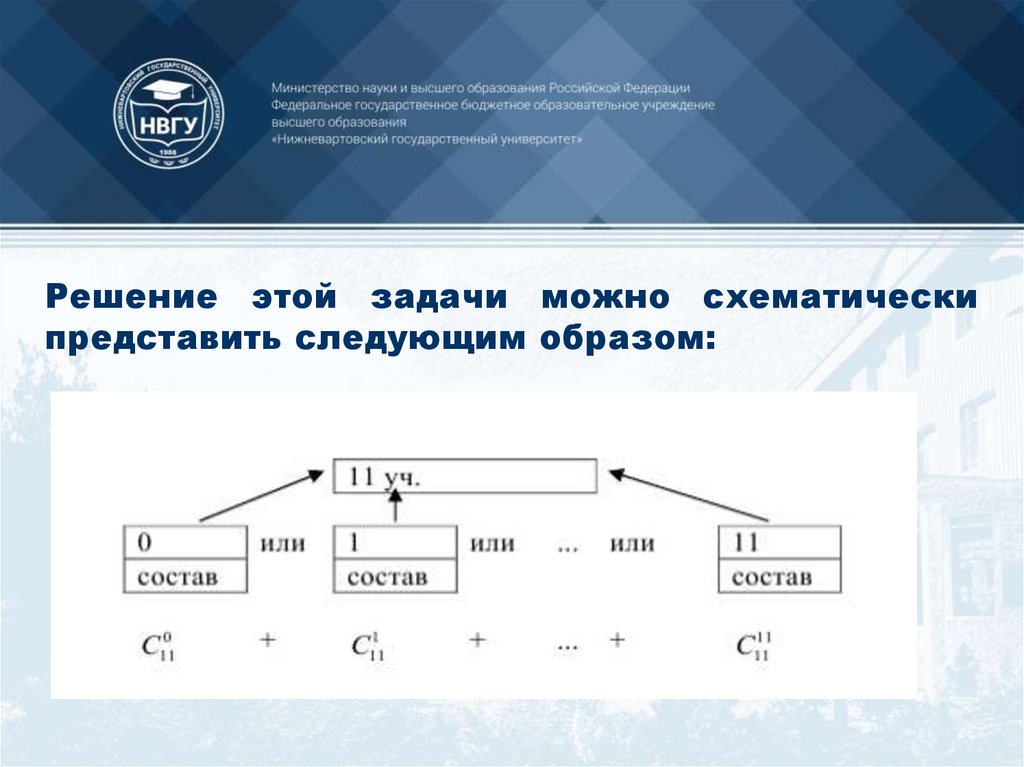
77.

Задача.
Сколько существует вариантов опроса 11
учащихся на одном занятии, если ни одни из
них не будет подвергнут опросу дважды и на
занятии
может
быть
опрошено
любое
количество учащихся, причем порядок, в
котором
опрашиваются
учащиеся,
безразличен?

78.

Решение.
I способ. Имеется генеральная совокупность
объема 11 учащихся. Преподаватель может не
опросить ни одного из 11 учащихся, что
является одним 0 из вариантов. Этому случаю
соответствует C 11 .
Преподаватель может опросить только одного
1
из учащихся, таких вариантов C 11 .

79.

Если преподаватель опросит двух учащихся,
2
то число вариантов опросаC 11 .
3
Для опроса трех учащихся существует C 11
вариантов и т. д.
Наконец,
могут
быть
опрошены
все
11
учащиеся. Число вариантов в этом случаеC 11.
Число всех возможных вариантов
можно найти по правилу сложения
C 11 C 11 ...... C 11 2
0
1
11
11
опроса

80.

Решение этой задачи можно схематически
представить следующим образом:

81.

II способ.
Имеется
генеральная
совокупность,
состоящая из 2 элементов: {a, b}, где a ученик опрошен, b - ученик не опрошен на
данном занятии. Опыт состоит в 11-кратном
выборе с возвращением одного из элементов
этого множества – каждый из 11 учеников
либо опрошен, либо не опрошен.

82.

В данной задаче важно не только то, какие
выбраны
элементы
множества
(сколько
учеников опрошено и сколько нет), но и в каком
порядке (т. е. какой именно ученик опрошен
или нет). Число способов такого выбора
определяется
числом
размещений
с
повторениями из 2 элементов по 11
11
A
2
2
11

83.

2.6. Сочетания с повторениями
Рассмотрим задачу о числе сочетаний с
повторениями: имеется по r одинаковых
предметов каждого из n различных типов;
сколькими способами можно выбрать m (m < r)
из этих (n · r) предметов?

84.

Определение.
Сочетаниями с повторениями называются
соединения из n элементов по m (выбор с
возвращением m элементов),
которые отличаются только составом и при
этом отдельные соединения могут содержать
повторяющиеся элементы.

85.

Задача.
Имеются 2 буквы A, 2 буквы B, 2 буквы C.
Сколькими способами можно выбрать две из
этих шести букв?
Решение
Существует 6 способов выбора 2 букв из 6 с
повторениями: (АА), (АВ), (АС), (ВС), (BB),
(СС).
Порядок
следования
букв
не
учитывается.

86.

Теорема.
Число
C
m
n
сочетаний с повторениями равно
(n m 10)!
C n C n m 1 m!(n 1)!
m
m

87.

Задача.
В технической библиотеке имеются книги по
математике, физике, химии и т. д., всего по 16
разделам науки.
Поступили
очередные
4
заказа
на
литературу. Сколько существует вариантов
такого заказа?

88.

Решение.
Так как 4 заказанные книги могут быть и из
одного раздела науки, и из разных
разделов,
при
этом
порядок
выбора
разделов не важен, то число вариантов
заказа определяется числом сочетаний с
повторениями из 16 элементов по 4, т. е.
19!
19 18 17 16
C 16 C 16 4 1 C 19 4!15! 1 2 3 4 3876
4
m
4

89.

Задача.
В кондитерском магазине продавались 4
сорта
пирожных:
наполеоны,
эклеры,
песочные и слоеные.
Сколькими способами можно купить 7
пирожных?

90.

Решение.
Очевидно, что порядок, в котором выбираются
пирожные,
не
существен,
причем
в
комбинации могут входить
повторяющиеся
элементы (например, можно купить 7 эклеров).
Следовательно, число способов покупки 7
пирожных определяется числом сочетаний с
повторениями из 4 элементов по 7, т.е.
10!
C 4 C 7 4 1 C 10 7!3! 120
7
7
7

91.

2.7. Комбинаторика разбиений
Рассмотрим в этом классе задач две
следующие задачи:
1. Даны n различных предметов и k
различных групп. Сколькими способами
можно распределить n различных предметов
по k различным группам, если допускаются
пустые группы. Ниже покажем, что число
n
способов равно
k

92.

2. Даны n различных предметов и k
различных
групп.
Сколькими
способами
можно распределить n различных предметов
по k группам, если в первой группе
n1!n 2 !.....n k !
предметов, во второй - n 2 , в k-й - n k
Где
n n .... n n
1
2
k
Ниже покажем, что число способов равно
n!
n1! n 2 !....n k !

93.

Рассмотрим решение первой задачи.
Пусть генеральной совокупностью будет k различных
групп {1,2,..., k}. Можно считать, что опыт состоит в nкратном выборе с возвращением номера группы для
каждого предмета. Заметим, что поскольку предметы
разные, то важно не только, какие группы выбираются
для предметов, но и в каком порядке выбираются эти
группы. Таким образом, число способов разбить n
различных предметов на k групп определяется числом
размещений с повторениями и k элементов по n:
A n
m
n
m

94.

Рассмотрим решение второй задачи.
Разбиение n предметов по k группам можно выполнить
следующим образом. Сначала положим все n предметов
в ряд. После этого возьмем первыеn
предметов
1
и поместим их в первую группу, вторые
2 предмета - во
k
вторую группу ,…, последние
предметов в k-ю
группу.
Ясно, что меняя положение предметов в ряду, можно
получить всевозможные разбиения предметов.
n
n
n

95.

Так как число перестановок из n элементов равно n!,
то число расположения предметов в ряд равно n! При
этом заметим, что любая перестановка первых
1
предметов ничего не меняет, так же как и вторых n 2
,…, и последних k
В силу правила произведения получим n1!n 2 !...., n k !)
n
n
перестановок предметов, не меняющих результата
раздела. Таким образом, число способов разбиения
на группы равно
P n (n1, n 2,...., n k )
n!
n1! n 2 !...n k !

96.

Формула совпадает с формулой для числа перестановок
с повторениями. К этому же результату можно прийти
иначе. Первые n1 предметов выбираем из n предметов.
Так как порядок выбранных предметов безразличен, то
1
имеет C n
выборов. После этого следующие
n
предмета выбираем из оставшихся n – n1
n2
1
Это можно сделать C n
способами, и т. д.
n n
1

97.

n
Наконец, последние
предметов выбираем из
k
nk
оставшихся k . Это можно сделать
, т. е.
C
nk
единственным способом.
По правилу произведения получаем, что число способов
разбиения на группы равно
n
n !(n n1)...n k
n!
n1 n 2 ,....., n k
C n1C n n 1 C n k !(n )! !... ! ! ! !... ! .
n1 n1 n 2 n k n k n1 n 2 n k
Как видим, задачи о разбиениях привели
известным формулам комбинаторики.
к
уже

98.

Задача.
7
одинаковых
шариков
случайным
образом
рассыпаются по 4 лункам (в одну лунку может
поместиться любое число шаров).
Сколько
существует
различных
способов
распределения 7 шариков по 4 лункам?
Решение.
Мы имеем 7 шариков, которые распределяем по 4
лункам (лунки могут быть пустые), т. е. это
соответствует первой задаче о разбиениях, число
способов равно
4 16348
7

99.

Задача.
При игре в домино 4 игрока делят поровну 28
костей. Сколькими способами они могут это
сделать?
Решение.
Это задача о разделе 28 костей между 4
игроками по 7 костей.
Используя полученную выше формулу для
числа способов такого раздела (задача 2),
имеем
28!
47 10
15
7!7!7!7!

100.

2.8. Рекомендации по решению задач
Решение комбинаторных задач представляет известную
трудность для начинающих. Причин много, но одна из
них
очевидна
–
при
изложении
комбинаторики
используется
своя
специфическая
терминология
(генеральная совокупность, выборка, правила выбора). В
задаче же этих терминов, как правило, нет –
сформулирована она на обычном литературном языке и
комбинаторные понятия присутствуют в ней в неявной
форме. Поэтому после усвоения содержания задачи
нужно ее «перевести» на математический язык.

101.

Для этого необходимо выяснить,
1) что является генеральной совокупностью - она всегда
будет присутствовать в задаче, т. е. комбинаторные
задачи связаны с выбором объектов, а этот выбор из
чего-то (генеральной совокупности) производится; каков
объем генеральной совокупности;
2) одна или несколько генеральных совокупностей;
3) что является выборкой и каков объем выборки;
4) правила выбора: допустимы или нет повторы, важен
ли порядок выбираемых элементов, возможно ли
изменение состава.

102.

После
этого
полезно
для
себя
переформулировать
задачу
на
языке
генеральных совокупностей и выборок. В
зависимости от ситуации выбрать нужную
формулу (см. таблицу). Иногда в более
сложных задачах приходится использовать
совместно несколько формул.

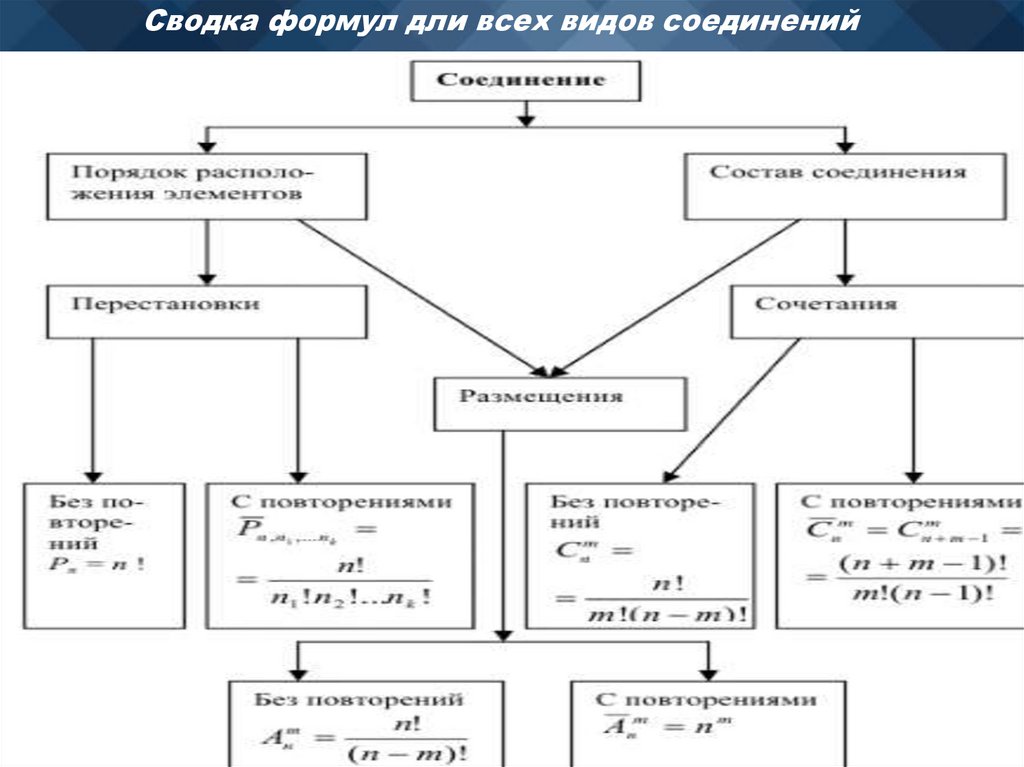
103.

Сводка формул дли всех видов соединений

104.

105.

106.

107.

108.

109.

110.

111.

112.

113.

114.

115.

116.

117.

118.

119.

120.

121.

122.

123.

124.

125.

126.

127.

128.

129.

Решение
задачи.
Составим таблицу и отразим в ней условия задачи,
заполнив соответствующие клетки цифрами 0 и 1 в
зависимости
от
того,
ложно
или
истинно
соответствующее высказывание.
Так как музыкантов
трoе, инструментов шесть и каждый владеет только двумя
инструментами, получается, что каждый музыкант играет
на инструментах, которыми остальные не владеют.
Из условия 4 следует, что Смит не играет ни на альте, ни
на трубе, а из условий 3 и 5, что Браун не умеет играть на
скрипке,
флейте,
трубе
и
гобое.
Следовательно,
инструменты Брауна — альт и кларнет. Занесем это в
таблицу, а оставшиеся клетки столбцов "альт" и "кларнет"
заполним нулями:

130.

скрипка
Браун
флейта
0
0
альт
кларнет
1
1
Смит
0
0
Вессон
0
0
гобой
труба
0
0
0
Из таблицы видно, что на трубе может играть только
Вессон.

131.

Из условий 1 и 2 следует, что Смит не скрипач. Так как на
скрипке не играет ни Браун, ни Смит, то скрипачом является
Вессон. Оба инструмента, на которых играет Вессон, теперь
определены, поэтому остальные клетки строки "Вессон" можно
заполнить нулями:
скрипка
флейта
Браун
0
0
Смит
0
Вессон
1
0
альт
кларнет
1
1
0
0
0
0
гобой
0
труба
0
0
0
1
Из таблицы видно, что играть на флейте и на гобое может
только Смит.

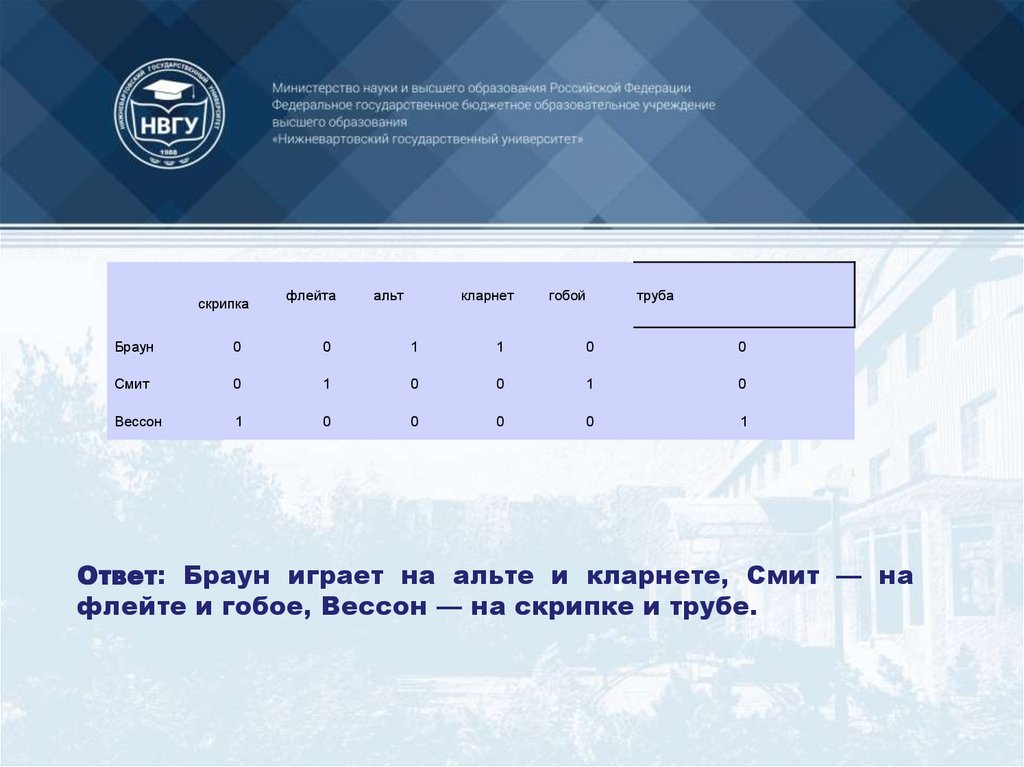
132.

скрипка
флейта
альт
кларнет
гобой
труба
Браун
0
0
1
1
0
0
Смит
0
1
0
0
1
0
Вессон
1
0
0
0
0
1
Ответ: Браун играет на альте и кларнете, Смит — на
флейте и гобое, Вессон — на скрипке и трубе.

133.

Задача "Одноклассники".
Три одноклассника — Влад, Тимур и Юра, встретились
спустя 10 лет после окончания школы. Выяснилось, что
один из них стал врачом, другой физиком, а третий
юристом. Один полюбил туризм, другой бег, страсть
третьего — регби.
Юра сказал, что на туризм ему не хватает времени,
хотя его сестра — единственный врач в семье, заядлый
турист. Врач сказал, что он разделяет увлечение
коллеги.
Забавно, но у двоих из друзей в названиях их
профессий и увлечений не встречается ни одна буква их
имен. Определите, кто чем любит заниматься в
свободное время и у кого какая профессия.

134.

Здесь исходные данные разбиваются на тройки (имя —
профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он
не врач. Из слов врача следует, что он турист.
Имя
Юра
Профессия
врач
Увлечение
туризм

135.

Буква "а", присутствующая в слове "врач", указывает на то,
что Влад тоже не врач, следовательно врач — Тимур. В его
имени есть буквы "т" и "р", встречающиеся в слове "туризм",
следовательно второй из друзей, в названиях профессии и
увлечения которого не встречается ни одна буква его имени —
Юра. Юра не юрист и не регбист, так как в его имени
содержатся буквы "ю" и "р". Следовательно, окончательно
имеем:
Имя
Юра
Тимур
Влад
Профессия
физик
врач
юрист
Увлечение
бег
туризм
регби
Ответ. Влад — юрист и регбист, Тимур — врач и турист,
Юра — физик и бегун.

136.

"Цветы и девочки".
Три девочки — Роза, Маргарита и Анюта представили на
конкурс цветоводов корзины выращенных ими роз,
маргариток и анютиных глазок. Девочка, вырастившая
маргаритки, обратила внимание Розы на то, что ни у одной
из девочек имя не совпадает с названием любимых цветов.
Какие цветы вырастила каждая из девочек?

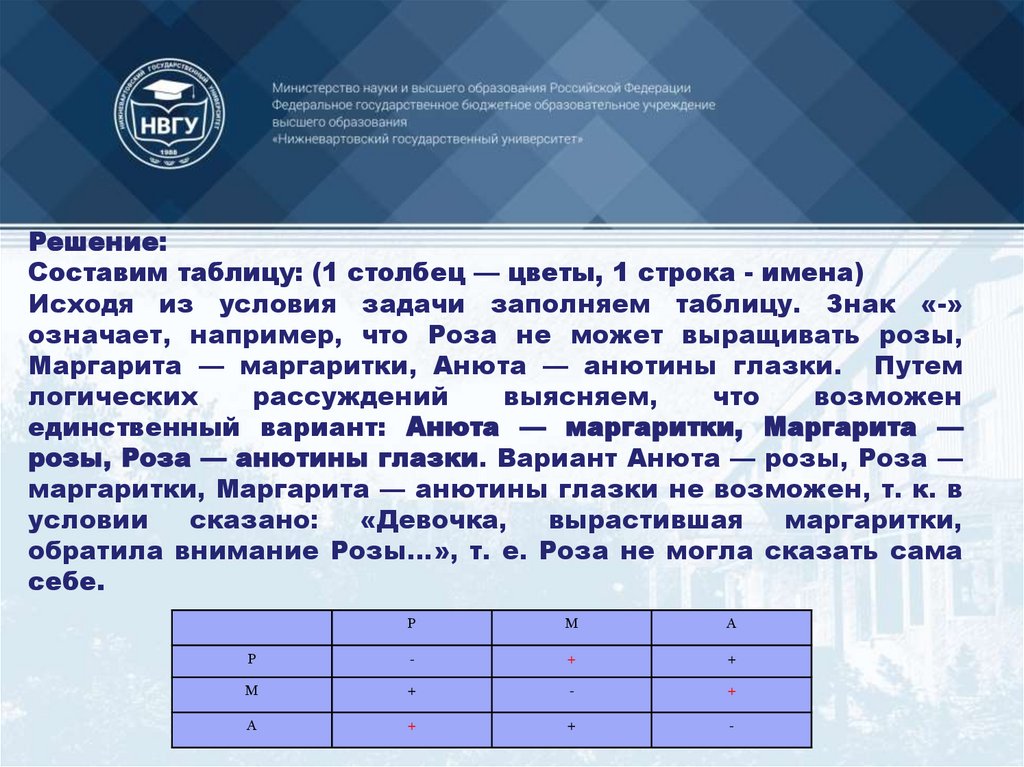
137.

Решение:
Составим таблицу: (1 столбец — цветы, 1 строка - имена)
Исходя из условия задачи заполняем таблицу. Знак «-»
означает, например, что Роза не может выращивать розы,
Маргарита — маргаритки, Анюта — анютины глазки. Путем
логических
рассуждений
выясняем,
что
возможен
единственный вариант: Анюта — маргаритки, Маргарита —
розы, Роза — анютины глазки. Вариант Анюта — розы, Роза —
маргаритки, Маргарита — анютины глазки не возможен, т. к. в
условии
сказано:
«Девочка,
вырастившая
маргаритки,
обратила внимание Розы...», т. е. Роза не могла сказать сама
себе.
Р
М
А
Р
-
+
+
М
+
-
+
А
+
+
-

138.

Задача "Дочери писательницы".
Три дочери писательницы Дорис Кей — Джуди, Айрис и
Линда, тоже очень талантливы. Они приобрели известность в
разных видах искусств — пении, балете и кино. Все они
живут в разных городах, поэтому Дорис часто звонит им в
Париж, Рим и Чикаго. Известно, что: Джуди живет не в
Париже, а Линда — не в Риме; Парижанка не снимается в
кино; та, кто живет в Риме, певица; Линда равнодушна к
балету.
Где живет Айрис, и какова ее профессия?

139.

При решении таких задач удобно
составлять таблицу следующего
вида:
Известно, что:
1) Джуди живет не в Париже, а Линда — не в Риме;
2) парижанка не снимается в кино;
3) та, кто живет в Риме, певица;
4) Линда равнодушна к балету.
Где живет Айрис и какова ее профессия?
Париж
Рим
Чикаго
Пение
Балет
Кино
—
+
—
Джуди
+
—
—
+
—
—
Айрис
—
+
—
—
—
+
Линда
—
—
+
Ответ
Айрис — балерина. Она живет в Париже.

140.

Кто изучал логику? На вопрос, кто из
трех учащихся - Антон, Борис или
Виктор - изучал логику, учитель,
преподававший логику, ответил: "Если
логику изучал Антон, то изучал и Боря,
но наверное, что если изучал Витя, то
изучал и Боря". Кто же изучал, а кто не
изучал логику?

141.

Обозначим буквой А высказывание "Антон изучал логику" ,
буквой В высказывание "Борис изучал логику", буквой С
высказывание "Виктор изучал логику". Тогда высказывание
учителя можно записать так:
. Преобразуем эту запись, освободившись от скобок:

142.

Поскольку утверждение учителя мы, конечно,
принимаем за истинное, истинными должны
быть и утверждения не А, не В и С.
Следовательно,
утверждение
А
ложно,
утверждение В тоже ложно, а утверждение С
истинно. Значит, логику изучал Виктор, а
Антон и Борис логику не изучали.

143.

Гражданин
Иванов
обвиняется
в
совершении
преступления при соучастии Петрова и Сидорова. Суд
присяжных в ходе слушания пришел к выводу, что
следствием доказано следующее:
1) если Иванов не виновен или виновен Петров, то
Сидоров виновен;
2) если Иванов не виновен, то Сидоров не виновен.
Присяжным требуется принять решение, виновен ли
Иванов. Достаточно ли у них для этого оснований?

144.

Решение. Обозначим буквой А высказывание "Иванов
виновен", буквой В высказывание "Петров виновен",
буквой С высказывание "Сидоров виновен". Тогда
имеющуюся
у
присяжных
информацию
можно
записать следующей формулой:
Составим для нее таблицу истинности.

145.

146.

Анализу подлежат те строки, в которых значение
составленной нами формулы равно 1. Мы видим, что во
всех этих случаях значение А равно 1. Следовательно,
Иванов виновен.
А вот для утверждения, что виновен Петров, оснований
недостаточно. Ведь значение 1 наша формула может
иметь и при ложном. Впрочем, нет оснований и
объявить Петрова невиновным. Если для перевода
условия задачи на языках математической логики
приходится использовать формулы с четырьмя, пятью
или еще большим числом переменных, таблица
истинности может насчитывать 16, 32 и более строк.
Для составления таких таблиц уже полезно применить
компьютер.

147.

вопрос, какой язык изучает каждый из
них, один ответил: "Вадим изучает
китайский, Сергей не изучает китайский,
а Михаил не изучает арабский".
Впоследствии выяснилось, что в этом
ответе только одно утверждение верно,
а два других ложны. Какой язык изучает
каждый из молодых людей?
Задача 12. "Друзья".
В поездке пятеро друзей — Антон,
Борис, Вадим, Дима и Гриша,
знакомились с попутчицей. Они
предложили ей отгадать их фамилии,
причём каждый из них высказал одно
истинное и одно ложное утверждение:
Дима сказал: "Моя фамилия —
Молотов, а фамилия Бориса — Хрущев".
Антон сказал: "Молотов — это моя
фамилия, а фамилия Вадима —
Брежнев".
Борис сказал: "Фамилия Вадима —
Тихонов, а моя фамилия — Молотов".
Вадим сказал: "Моя фамилия —
Брежнев, а фамилия Гриши — Чехов".

148.

Тимур и победитель олимпиады по
литературе занимаются плаванием;
Тимур и Камилла поздравили
победителя олимпиады по математике;
Ирена сожалеет о том, что у нее
остается мало времени на
литературу. Победителем какой
олимпиады стал каждый из ребят?
Задача 14
На очередном этапе гонок «Формула1» первые четыре места заняли
Шумахер, Алези, Хилл и Кулхард.
Опоздавший к месту награждения
телеоператор успел заснять пилотов,
занявших второе и третье места,
которые поливали друг друга
шампанским. В это время Шумахер с
четвертым гонщиком пожимали друг
другу руки. Далее в кадр попал мокрый
Хилл, поздравляющий пилота,
занявшего второе место. Напоследок
оператор снял сцену, в которой Шумахер
и Кулхард пытались вытащить на
пьедестал почета пилота, занявшего

149.

как они проведи лето.
- Ну, Балашов, ты, наконец, научился
плавать? – спросил Володя?
- О, еще как, - ответил Балашов, - могу
теперь посоревновался в плавании с
тобой и Аликом.
- Посмотрите, какой я гербарий собрал, сказал Петров, прерывая разговор
друзей, и достал из шкафа большую
папку.
Всем, особенно Лунину и Алику,
гербарий очень понравился. А Симонов
обещал показать товарищам собранную
им коллекцию минералов. Назовите
фамилию и имя каждого мальчика.
Задача 16.
Покупатель в каждом из
магазинов A, B, C и D сделал по одной
покупке и приобрел джойстик, дискеты,
бумагу и картридж. Известно, что в D не
было ни дискет, ни джойстика;
в C покупатель зашел, уже купив
дискету и бумагу; джойстик и картридж
были куплены не в A; в B покупатель

150.

зоотехник следил за их игрой.
Вяснилось, что тракторист в Москве не
бывал, остальные же едут в Москву не в
первый раз, а Юрий даже родился в
Москве. Николай всю дорогу на больших
остановках поезда покупал новые
газеты и журналы. По вечерам
комбайнер, оказавшийся старше
Михаила, рассказывал Ивану о
войне. Как звали каждого специалиста?
Задача 18.
В рабочем поселке живут и работают
девушки: Валя, Галя, Сима и
Женя. Двое из них – Валя и Галя – живут
вместе и на работу утром тоже ходят
вместе, так как места их работы
расположены вблизи друг от друга.
Специальности у девушек разные –
ткачиха, врач, секретарь и шофер. Женя
и Валя участвуют в хоре при дворце
культуры. Врач решила познакомить
Галю со своей подругой, чудесной
девушкой-шофером, с которой Галя
раньше не встречалась.

151.

заводе выделили путевку в один из
санаториев Сочи. Борисов своим
советом помог Левину выбрать
новейшую модель
радиоприемника. Жена художника, зная,
что Иванов в магазине радиотоваров,
позвонила Борисову и попросила
передать Иванову, что ее муж заболел,
и чтобы Иванов зашел к ним. Приемник
очень понравился Левину, и он
пригласил продавца на премьеру
спектакля «Вишневый сад». Требуется
узнать, кто из друзей имеет ту или иную
специальность.
Задача 20.
Дина, Соня, Коля, Рома и Миша учатся
в институте. Их фамилии – Бойченко,
Карпенко, Лысенко, Савченко и
Шевченко. Мать Ромы умерла. Родители
дины никогда не встречались с
родителями Коли. Студенты Шевченко и
Бойченко играют в одной баскетбольной
команде. Услышав, что родители
Карпенко собираются поехать за город,

152.

Морозовой живет ее подруга Ольга
Бугрова. Леонид Соболев живет по
соседству с домом Валентины
Морозовой. Если из номера дома
Леонида Соболева вычесть номер дома
Ольги Бугровой, то получится число,
обозначающее номер дома, в котором
живет Василий Рябинин. Если умножить
номер дома, в котором живет Василий
Рябинин, на номер дома, в котором
живет Валентина Морозова, то
получится число, в точности
соответствующее номеру дома, в
котором живет Иван Митков.
Номер дома Ильи Ковалева нечетный,
а его друга Николая Глебова, живущего
напротив него, - четный. Указать номер
дома, в котором живет каждый из
указанных друзей, если известно, что
номер дома Марии Зверевой в три раза
больше номера дома Василия
Рябинина.
Задача 22.

153.

из сестер Ивановых заняла первое
место, опередив Надю всего лишь на 0,2
секунды. В лыжном пробеге Надя не
участвовала, так как готовилась к
экзаменам. В фабричной многотиражке
были помещены портреты Ивановой и
Сафроновой – лучших гимнасток
фабрики. У Тани и у Нади одинаковые
лыжные костюмы.
Задача 24.
В областном городе проходили
соревнования по четырем видам спорта
– плаванию, тяжелой атлетике, хоккею и
волейболу. В этих соревнованиях
участвовали четыре ведущих
спортсмена: Пастухов, Михайлов,
Дмитриев и Никонов. Имена их были
следующие: Павел, Геннадий, Никита и
Дмитрий. Каждый спортсмен принимал
участие только в одном виде спорта, но
каждый стремился посетить
соревнования и по другим видам спорта
и «поболеть» за других участников.
Пастухов и Дмитриев присутствовали

154.

Пермяк старше Андреева, а одессит
старше Власова.
Быков и москвич сошли в Киеве, а
Власов и пермяк должны сойти в
Харькове.
Определить фамилию, профессию и
местожительство каждого пассажира.
Задача 26.
Алексей, Борис, Галина, Ирина,
Владимир и Екатерина приехали в
Москву. За шесть дней пребывания в
столице каждый успел побывать в
Третьяковской галерее, на стадионе в
Лужниках, в Большом театре, а также
сходить в кино, посетить Исторический
музей и покататься на речном трамвае
по Москве-реке.
Ежедневно все шестеро
разъезжались по разным местам. Так,
например, в первый день Владимир
посетил Исторический музей, а
Екатерина посмотрела кинокартину. Во
второй день Алексей побывал в
Лужниках, Галина же слушала оперу

155.

Корниенко испытывал самолет ИЛ, а
Мгеладзе – ЛА. В четвертый день
Сергеев поднялся в воздух на самолете
ЯК, а Пугачевский – на самолете МИГ.
Составьте таблицу испытаний
самолетов на все пять дней.
Задача 28.
Летом в нашем городе обувной
магазин закрывается каждый
понедельник, хозяйственный – каждый
вторник, продовольственный – каждый
четверг, а парфюмерный работает
только по понедельникам, средам и
пятницам. воскресенье все магазины в
городе закрыты. Однажды подруги Аня,
Рита, Катя и Дина отправились за
покупками, причем, каждая в свой
магазин.
По дороге они обменивались
впечатлениями.
Дина: «Я могла бы пойти в магазин и
вчера и завтра».
Аня: «Дина и я хотели пойти еще
раньше на этой неделе, но не было

156.

проиграл спартаковцам, но во втором
туре выиграл у «Авангарда». В третьем
туре «Торпедо» было свободно от игры,
одержав при этом дну победу и проиграв
другую встречу. В четвертом туре
свободной от игры был «Авангард»,
имевший в своем активе две победы при
трех сыгранных турах.
Прошлогодние чемпионы – динамовцы
– к этому времени сумели выиграть
только один матч. За победы, как
обычно, команда получала два очка, за
ничью – одно очко, за поражение – ноль
очков. Каких результатов добилась
каждая из команд в соревнованиях,
если встречи четвертого и пятого туров
закончились вничью?
Задача 30.
Три свидетеля дорожного
происшествия сообщили сведения о
скрывшемся нарушителе. Боб
утверждает, что тот был на синем
«Рено». Джон сказал, что нарушитель
ехал на черной «Тойоте», а Сэм сказал,

157.

158.

159.

160.

161.

162.

163.

164.

165.

166.

167.

168.

169.

170.

171.

172.

173.

174.

175.

176.

177.

178.

179.

180.

181.

182.

183.

184.

185.

186.

187.

188.

189.

190.

191.

192.

БЛАГОДАРЮ ЗА ВНИМАНИЕ