Элементы аналитической геометрии. Кривые второго порядка

1.

Дисциплина «Линейная
алгебра и геометрия»
Элементы аналитической геометрии
Кривые второго порядка

2.

Результаты текущей успеваемости 1 года обучения
за сентябрь
месяц
Литература
1. Шипачев В.С. Высшая математика. Полный курс в 2 т. Том 1: учебник
для академического бакалавриата/ В.С. Шипачев; под ред. А.Н.
Тихонова. – 4-ое изд., испр. и доп. – М.:Издательство Юрайт, 2016. –
С. 68-85
2. Шипачев В.С. Высшая математика : учебник для академического
бакалаври-ата /В.С.Шипачев; под ред.А.Н. Тихонова. – 8-ое изд.,
перераб. и доп. – М.:Издательство Юрайт, 2016. – С. 63-83
3. Ефимов Н.В. Краткий курс аналитической геометрии. – 14- е изд.,
испр. – М.:ФИЗМАТЛИТ, 2018. – С. 70-110

3.

Результаты текущей успеваемости 1 года обучения
за сентябрь месяц
1. Общее
уравнение
кривой
второго
порядка.
Канонические уравнения кривых второго порядка
2. Эллипс и его каноническое уравнение
3. Гипербола и ее каноническое уравнение
4. Парабола. Исследование
каноническому уравнению
форм
параболы
по
ее

4.

Количество проведенных
1. Общееконтрольных
уравнение кривой
второго порядка.
проверок
Ах2 + Вху + Су2 + Dx + Ey + F = 0, где А2 + В2 + С2 0,
В зависимости от значений коэффициентов общего
уравнения (*) оно может быть преобразовано с
помощью параллельного переноса и поворота
системы координат к одному из канонических видов,
каждому из которых соответствует определённый
класс плоских кривых.

5.

Количество проведенных
1. Общееконтрольных
уравнение кривой
второго порядка.
проверок
x
2
a
2
y
2
b
2
1
— пары пересекающихся
действительных прямых
x2 y2
2 1
2
a
b
x
2
a
2
y
2
b
2
у2 = 2рх
— эллипсы
x2 y 2
2 0
2
a
b
1
— мнимые эллипсы
x2 y2
2 0
2
a
b
— пары мнимых
пересекающихся прямых
-- гиперболы
х2= а2
- параболы (p > 0, q > 0)
х2= —а2
х2= 0
пары
параллельных
прямых
пары совпадающих
действительных
прямых

6.

Количество проведенных
2. Эллипс контрольных
и его каноническое
проверок уравнение.
Определение:
Эллипсом называется
множество точек плоскости, для которых
сумма расстояний до двух фиксированных
точек плоскости, называемых фокусами, есть
постоянная
величина,
большая,
чем
расстояние между фокусами.

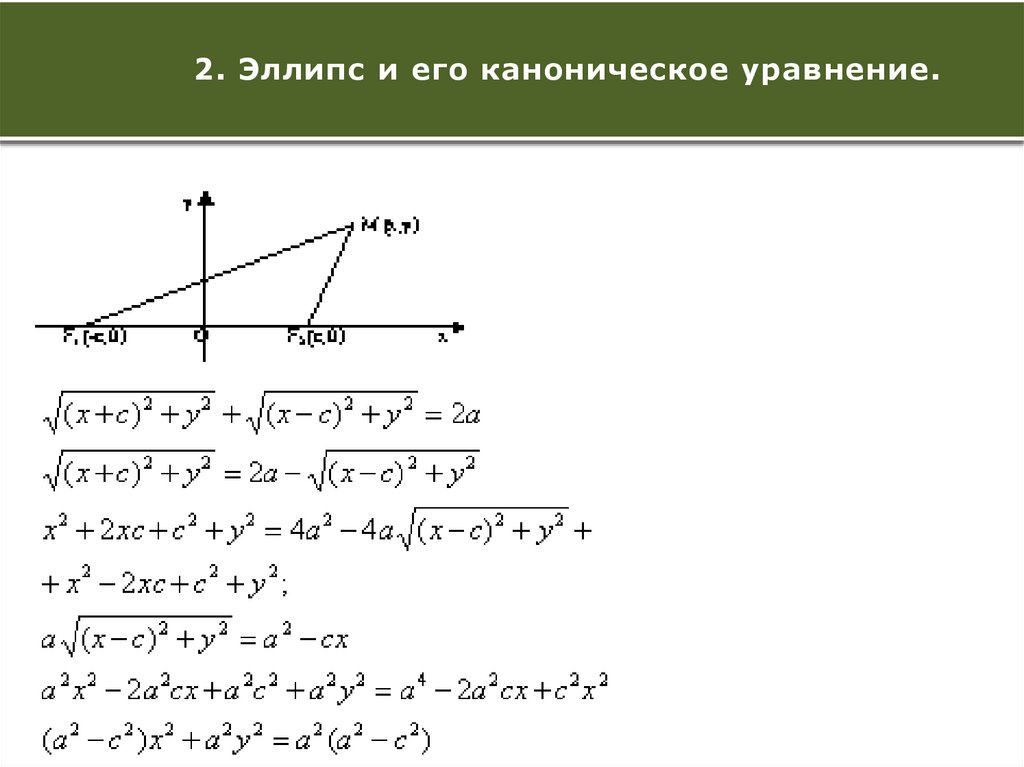
7.

Количество проведенных
2. Эллипс контрольных
и его каноническое
проверок уравнение.

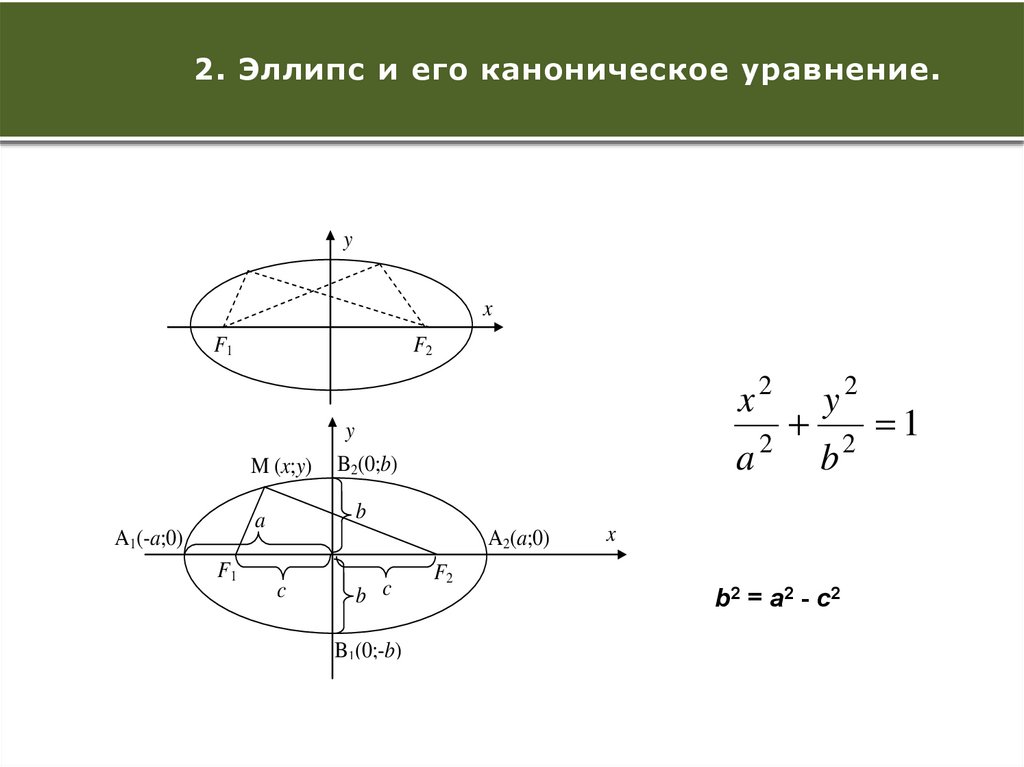
8.

Количество проведенных
2. Эллипс контрольных
и его каноническое
проверок уравнение.
y
x
F1
F2
x2
M (x;y)
F1
a
2
b
b
a
A1(-a;0)
y
B2(0;b)
y2
A2(a;0)
c
b c
B1(0;-b)
x
F2
b2 = a2 - c2
2
1

9.

Количество проведенных
2. Эллипсконтрольных
и его каноническое
уравнение
проверок
Определение: Отношение
эксцентриситетом эллипса.
c
Обозначается: ε a
0 ε 1
c
a
называется

10.

Количество проведенных
2. Эллипсконтрольных
и его каноническое
уравнение
проверок
Определение: Расстояния от произвольной
точки М (х;у), лежащей на эллипсе, до фокусов
называются фокальными радиусами этой
точки. Обозначаются r1 и r2. Определяются
по формулам:
r1 a εx
r2 a εx .

11.

Количество проведенных
Оптические
свойства
контрольных
проверокэллипса
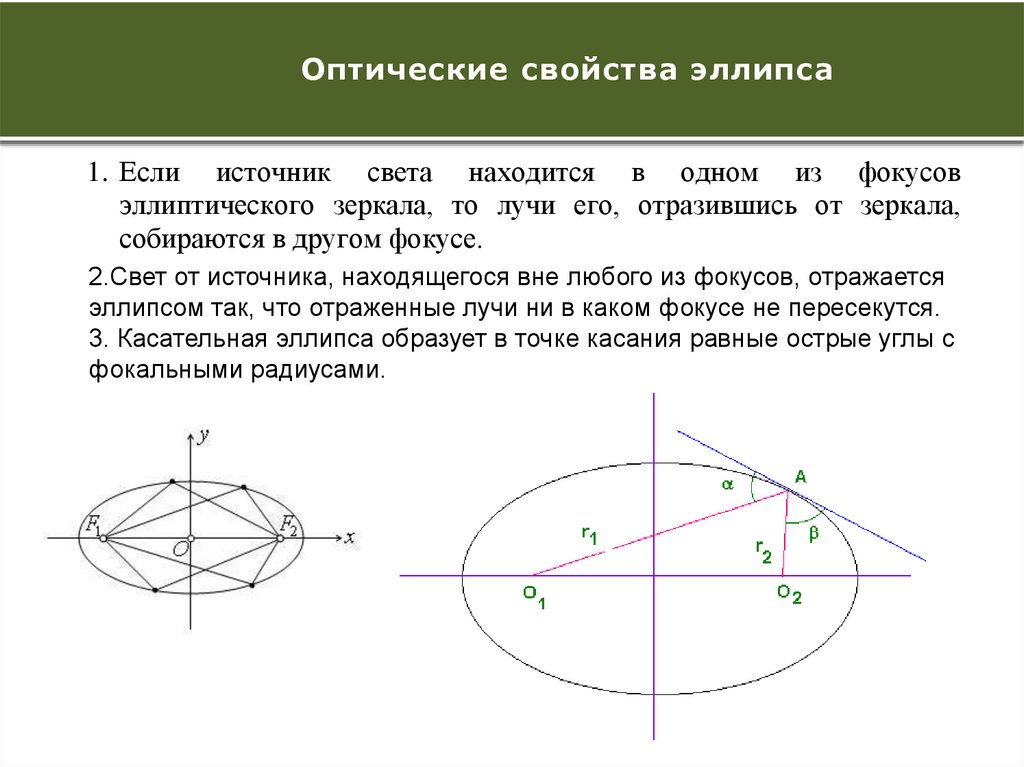
1. Если источник света находится в одном из фокусов
эллиптического зеркала, то лучи его, отразившись от зеркала,
собираются в другом фокусе.
2.Свет от источника, находящегося вне любого из фокусов, отражается
эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
3. Касательная эллипса образует в точке касания равные острые углы с
фокальными радиусами.

12.

Количество проведенных
Окружность
контрольных
проверок
Определение: Окружностью называется множество
точек плоскости, расстояние от которых до
фиксированной точки, называемой центром, есть
величина постоянная.
y
М (х;у)
у
b
( x a ) 2 ( y b) 2 R 2
С
нормальное уравнение окружности
x
a
x
x2 y2 R 2
каноническое уравнение окружности

13.

Количество проведенных
3. Гипербола
и ее каноническое
уравнение
контрольных
проверок
Определение: Гиперболой называется множество точек
плоскости, для которых разность расстояний до двух
фиксированных точек плоскости, называемых фокусами, есть
постоянная величина, меньшая, чем расстояние между
фокусами и не равная нулю (указанная разность берется по
абсолютной величине).
Гипербола задается уравнением:
x2
a
2
y2
b
2
1.

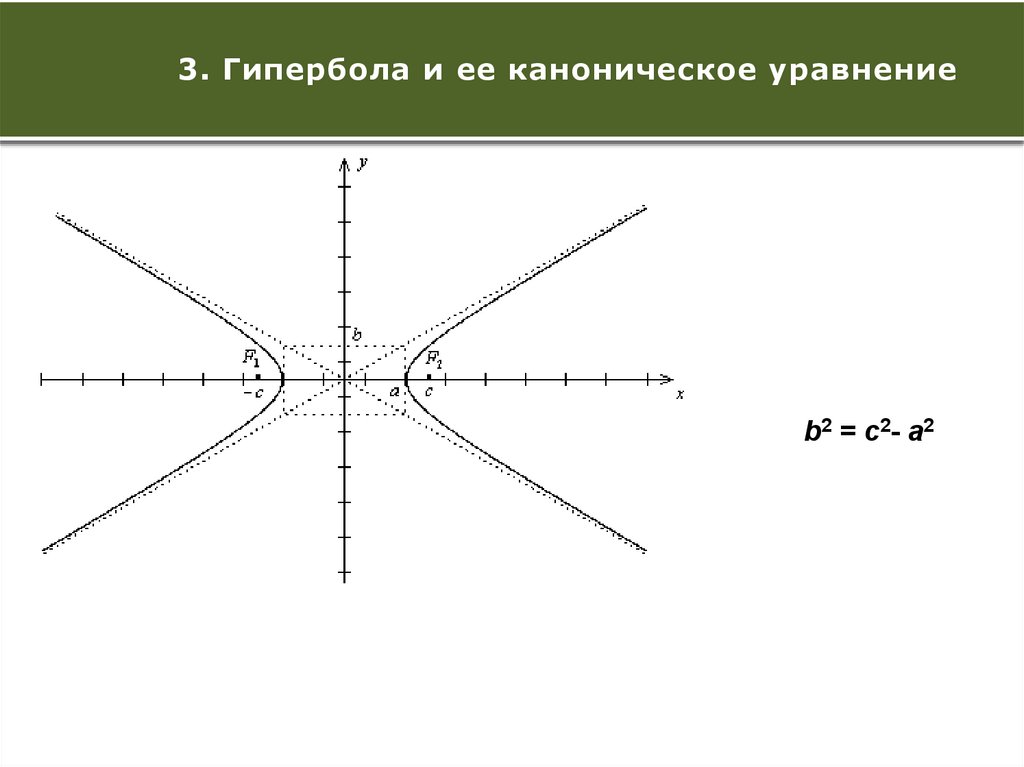
14.

Количество проведенных
3. Гипербола
и ее каноническое
уравнение
контрольных
проверок
b2 = c2- a2

15.

Количество проведенных
3. Гипербола
и ее каноническое
уравнение
контрольных
проверок
c
Определение: Отношение a называется эксцентриситетом гиперболы:
c
ε
a
(т.к. c > a , то
> 1)
Определение: Расстояния от произвольной точки М(х;у), лежащей на
гиперболе, до фокусов называются фокальными радиусами этой точки.
Фокальные радиусы определяются по формулам:
r1 εx a
r2 εx a - для точек правой ветви;
r1 (εx a )
- для точек левой ветви.
r2 (εx a )

16.

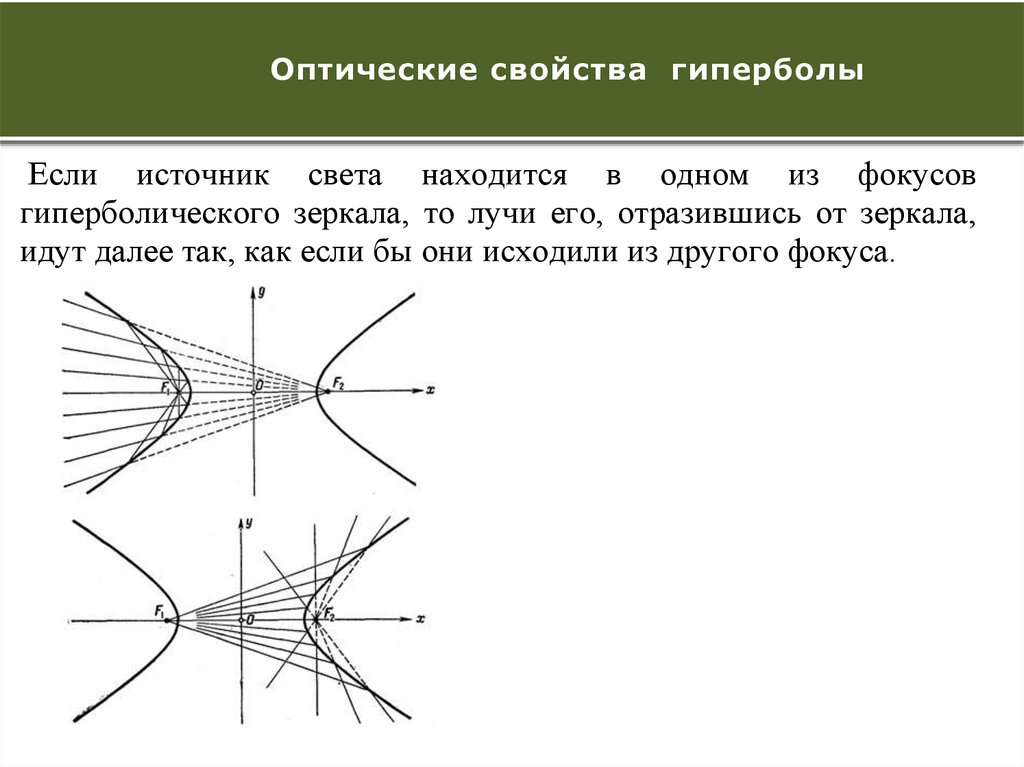
Количество проведенных
Оптические
свойства
гиперболы
контрольных
проверок
Если источник света находится в одном из фокусов
гиперболического зеркала, то лучи его, отразившись от зеркала,
идут далее так, как если бы они исходили из другого фокуса.

17.

Количество проведенных
4. Парабола
контрольных
проверок
Определение: Параболой называется множество точек плоскости,
равноудаленных от данной точки плоскости, называемой фокусом,
и от данной прямой, называемой директрисой
(фокус F не принадлежит директрисе).
y
D
у2 = 2рх
M(x;y)
p/2
p/2
r
x
x
p
2
(1) - каноническое уравнение
параболы; р - параметр
параболы (p>0)
(2) - уравнение директрисы
F(p/2;0)
p
параболы.
D
где параметр р - расстояние от F до директрисы.

18.

Количество проведенных
4. Парабола
контрольных
проверок
Определение: Расстояние от фокуса F до произвольной
точки М(х;у) называется фокальным радиусом:
r x p/2.

19.

Количество проведенных
Парабола
контрольных
проверок
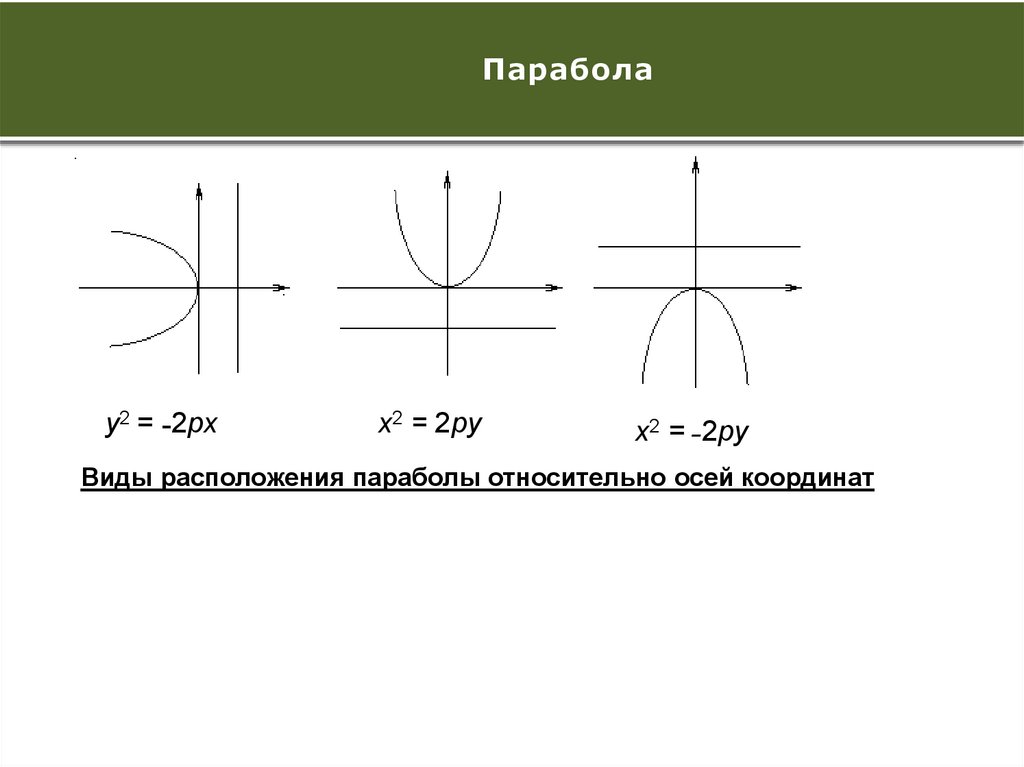
y2 = ˗2px
x2 = 2py
x2 = ˗2py
Виды расположения параболы относительно осей координат

20.

Количество проведенных
Оптические
свойства
параболы
контрольных
проверок
Если источник света находится в фокусе параболического
зеркала, то лучи его, отразившись от зеркала, идут параллельно
оси.

21.

Количество проведенных
Задачи
контрольных
проверок
Задача 1:
Составить уравнение окружности с
центром в точке С (-2;3) и радиусом R = 5.

22.

Количество проведенных
Задачи
контрольных
проверок
Задача 2: Составить уравнение окружности, имеющей
центр в точке
С (1;-2) и проходящей через точку М (3;4).

23.

Количество проведенных
Задачи
контрольных
проверок
Задача: Найти каноническое уравнение эллипса,
зная, что его большая полуось равна 4, а
эксцентриситет равен ½.
x2
a
2
c
ε
a
y2
b
2
1
b2 a 2 c 2
c 1
a 2
x2 y2
2 1
16 b
c 1
4 2
b2 16 4 12,
c 2
x2 y2
1
16 12

24.

Количество проведенных
Задачи
контрольных
проверок
Задача:
Составить уравнение гиперболы, если
расстояние между фокусами 2с = 26, а =13/12 .
ε
c
a
b2 = c 2 - a2
13 13
a
12
а = 12
b2 = 132- 122 = 169 - 144 = 25
y2
x2
1
144 25

25.

Количество проведенных
Задачи
контрольных
проверок
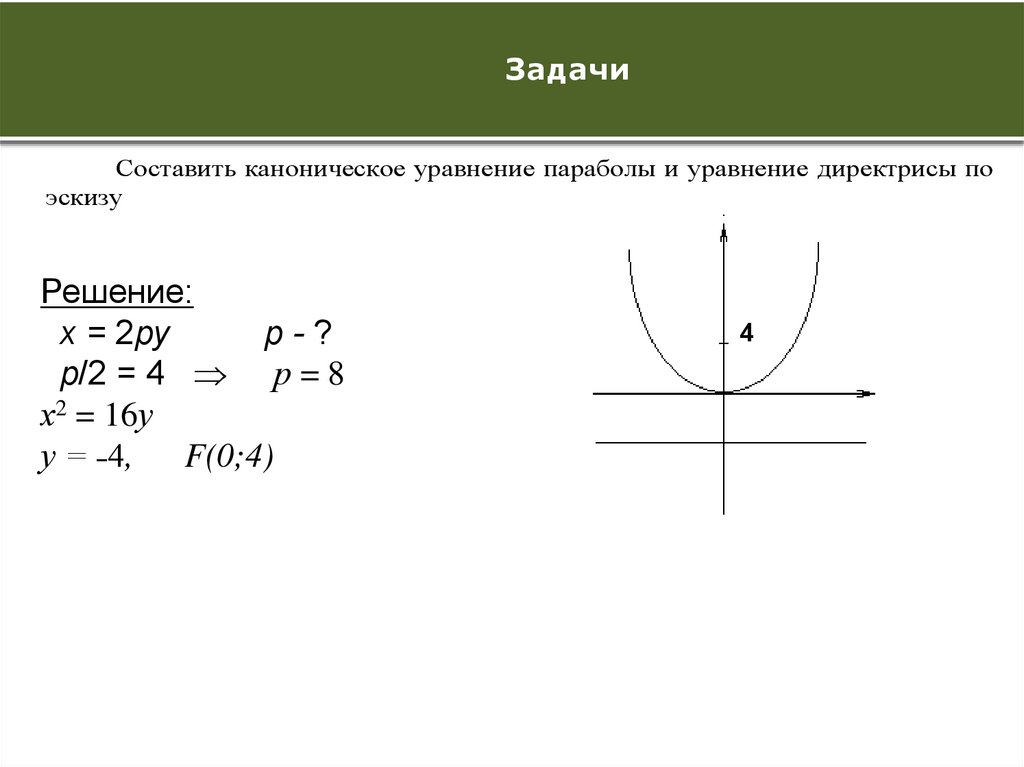
Составить каноническое уравнение параболы и уравнение директрисы по
эскизу
Решение:
х = 2ру
р-?
р/2 = 4 р = 8
х2 = 16у
у = ˗4, F(0;4)
4