Прямые и плоскости в пространстве

1.

2.

Плоскость — это геометрическая фигура,
которая не имеет длины, ширины и
высоты. Она является одномерным
аналогом пространства и состоит из
бесконечного множества точек,
упорядоченных в двух измерениях.
Прямая – это линия, продолжающаяся
бесконечно в обе стороны, любая часть
которой, ограниченная двумя точками,
является отрезком.
Способы задания плоскости:
• тремя точками, не лежащими на одной прямой;
• прямой и точкой вне ее;
• двумя пересекающимися прямыми.

3.

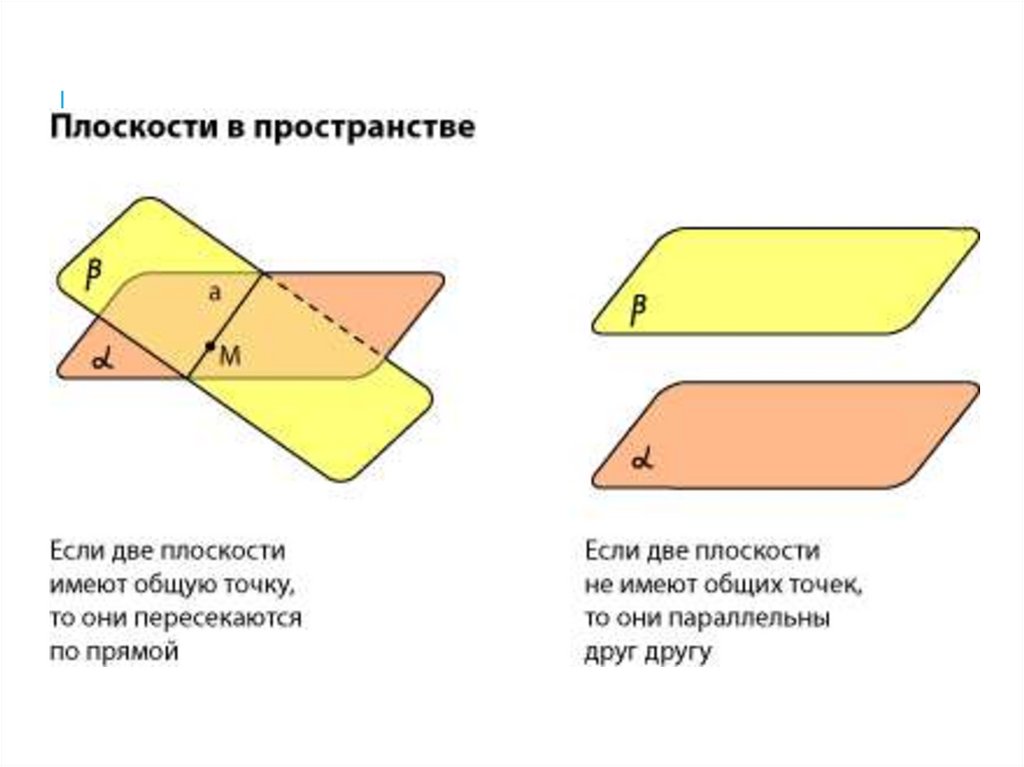
РАСПОЛОЖЕНИЕ ДВУХ
ПЛОСКОСТЕЙ
• плоскости не имеют общих точек, не
пересекаются. В этом случае говорят, что
плоскости параллельны;
• имеют общие точки, пересекаются. В этом
случае утверждается, что две плоскости
пересекаются по прямой.
Это означает, что общие точки двух
пересекающихся плоскостей составляют
некоторую прямую.

4.

5.

6.

7.

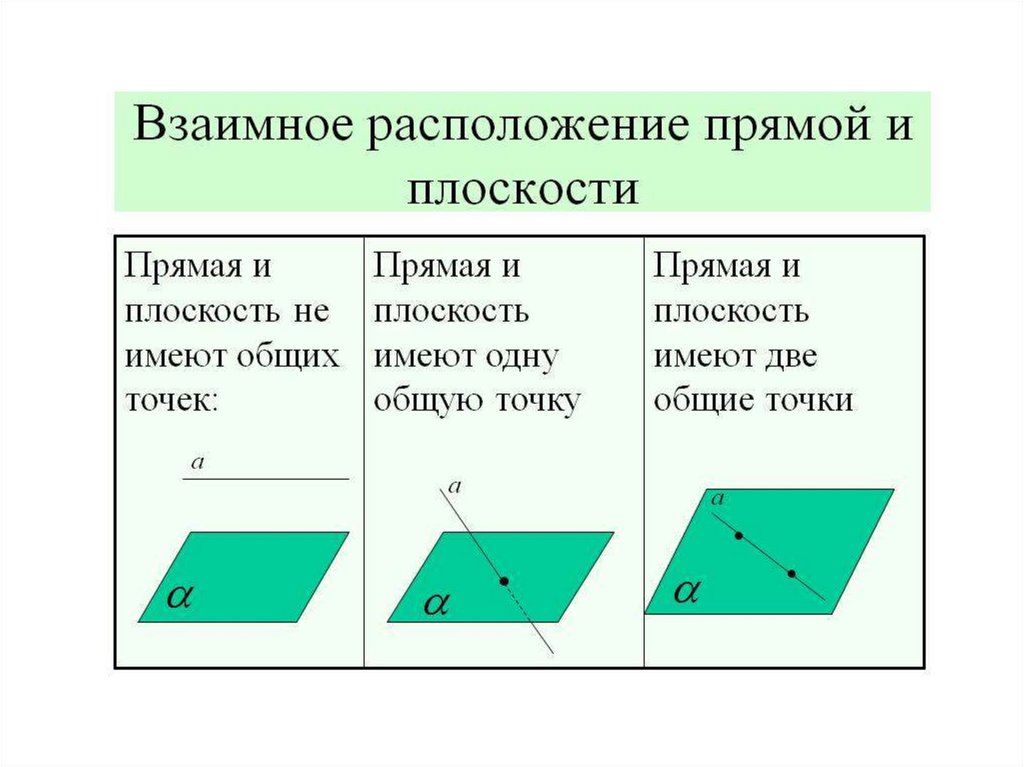
РАСПОЛОЖЕНИЕ ПРЯМОЙ И
ПЛОСКОСТИ
• прямая может лежать в плоскости. При этом
если две точки прямой принадлежат
плоскости, то вся прямая целиком лежит в
этой плоскости;
• прямая может иметь с плоскостью ровно
одну общую точку: прямая пересекает
плоскость;
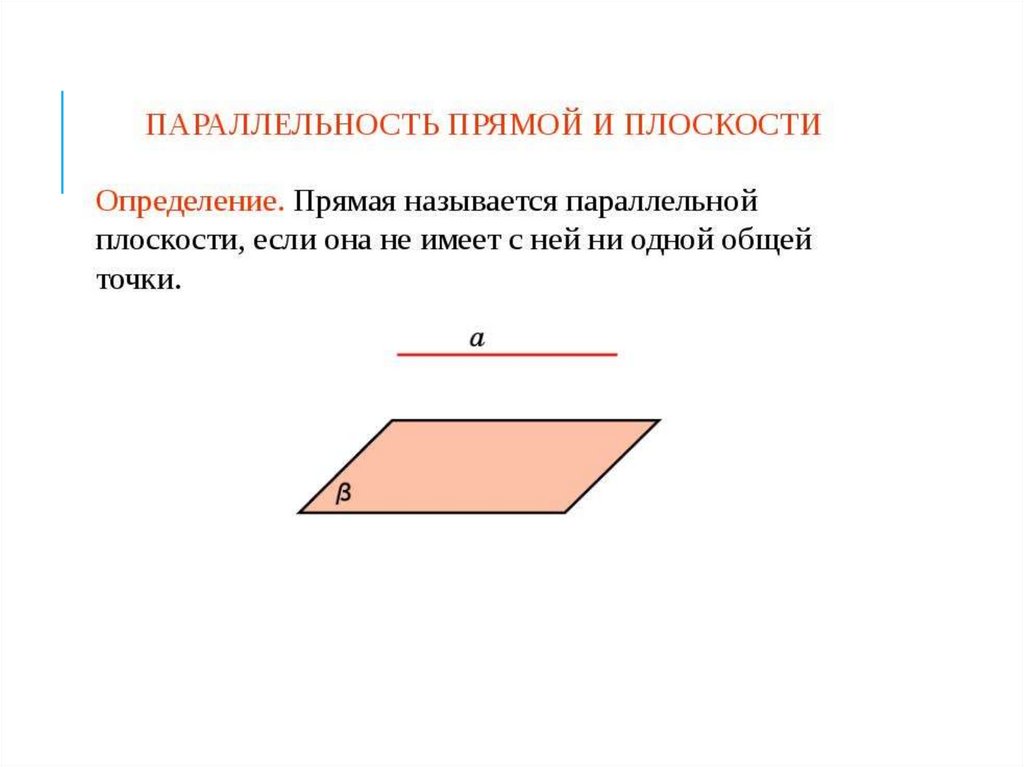
• прямая и плоскость не имеют общих точек:
прямая параллельна плоскости.

8.

9.

ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ
ПРЯМЫХ И ПЛОСКОСТЕЙ
1. Пусть прямая не лежит в некоторой
плоскости и параллельна какой-то прямой
этой плоскости. Тогда исходная прямая
параллельна данной плоскости.
2. Пусть прямая параллельна некоторой
плоскости. Если через эту прямую провести
еще одну плоскость, которая пересекает
заданную, то их линия пересечения
параллельна исходной прямой.

10.

11.

3. Пусть две плоскости параллельны, а третья
плоскость их пересекает по некоторым
прямым. Тогда эти прямые параллельны.
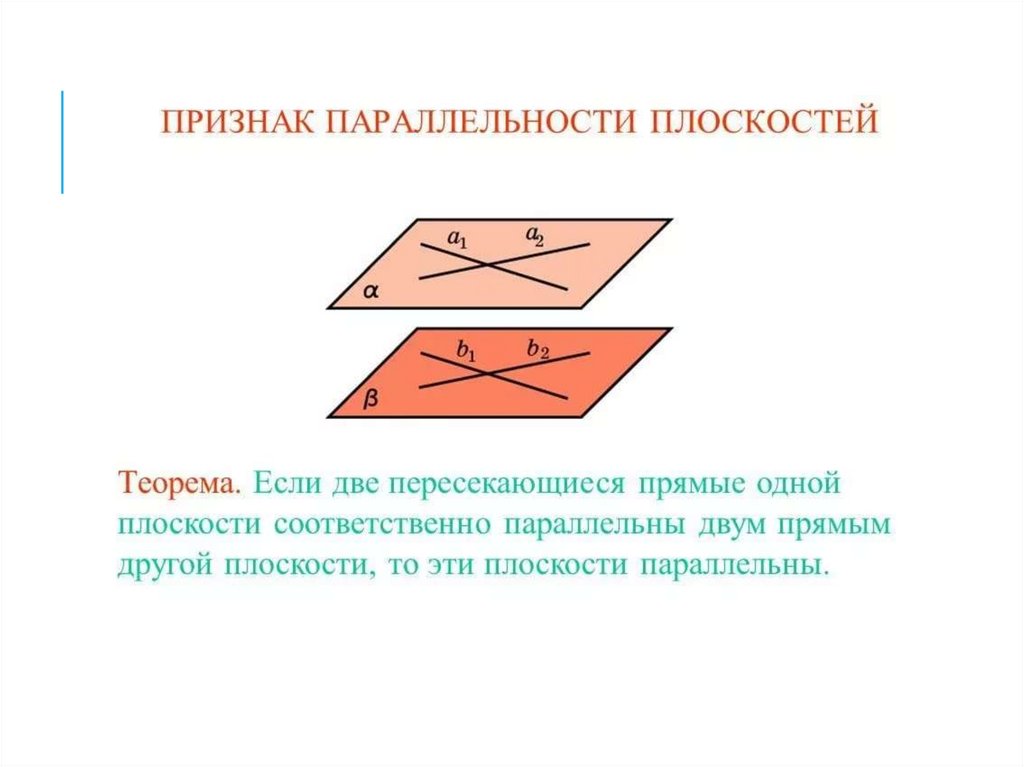
4. Пусть в одной плоскости нашлись две
пересекающиеся прямые, которые
соответственно параллельны двум прямым
другой плоскости. Тогда эти две плоскости
параллельны.

12.

13.

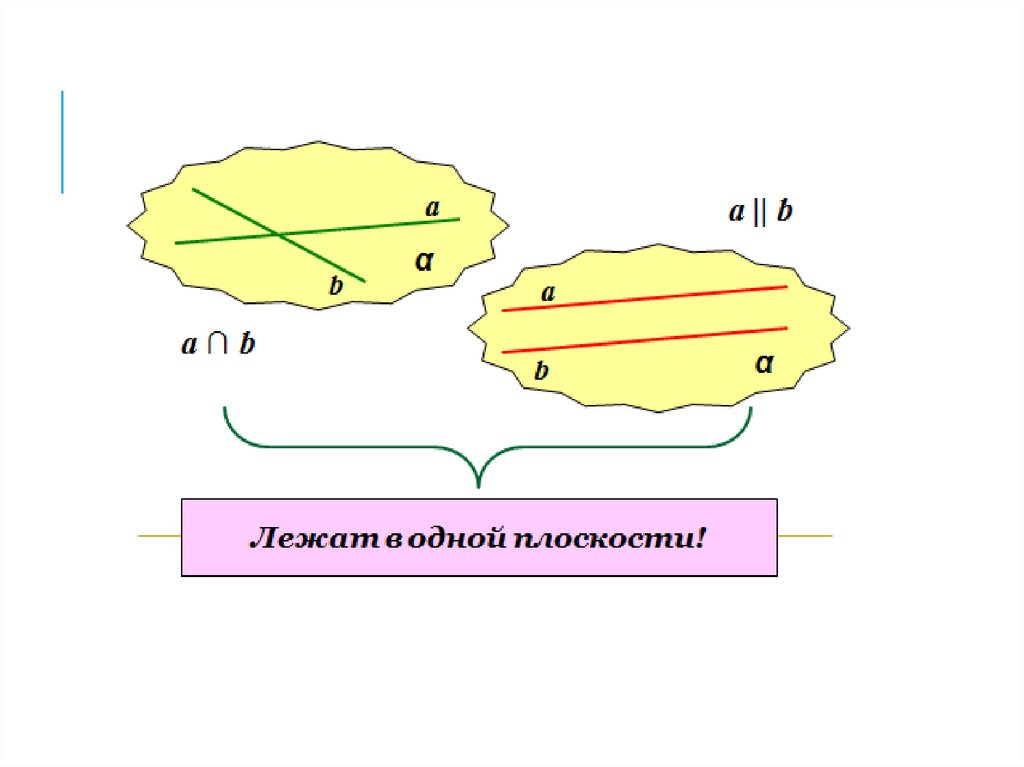
РАСПОЛОЖЕНИЕ ДВУХ
ПРЯМЫХ
• две прямые лежат в одной плоскости. Тогда
есть две возможности: либо они пересекаются,
т. е. имеют одну общую точку, либо
параллельны, т.е. не имеют общих точек (и не
забудьте, что при этом прямые лежат в одной
плоскости);
• не лежат в одной плоскости. Такие прямые
называются скрещивающимися.
Подразумевается, скрещивающиеся прямые не
имеют общих точек, иначе они лежали бы в
одной плоскости.

14.

15.

Прямые называются параллельными, если они
лежат в одной плоскости и не имеют точек пересечения
Свойства:
• Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная
данной, и притом только одна
• Если одна из параллельных прямых пересекает
плоскость, то и вторая прямая также пересекает
эту плоскость
• Если две прямые параллельны третьей прямой,
то они параллельны
Две параллельные прямые, как и две пересекающиеся
прямые, задают плоскость

16.

17.

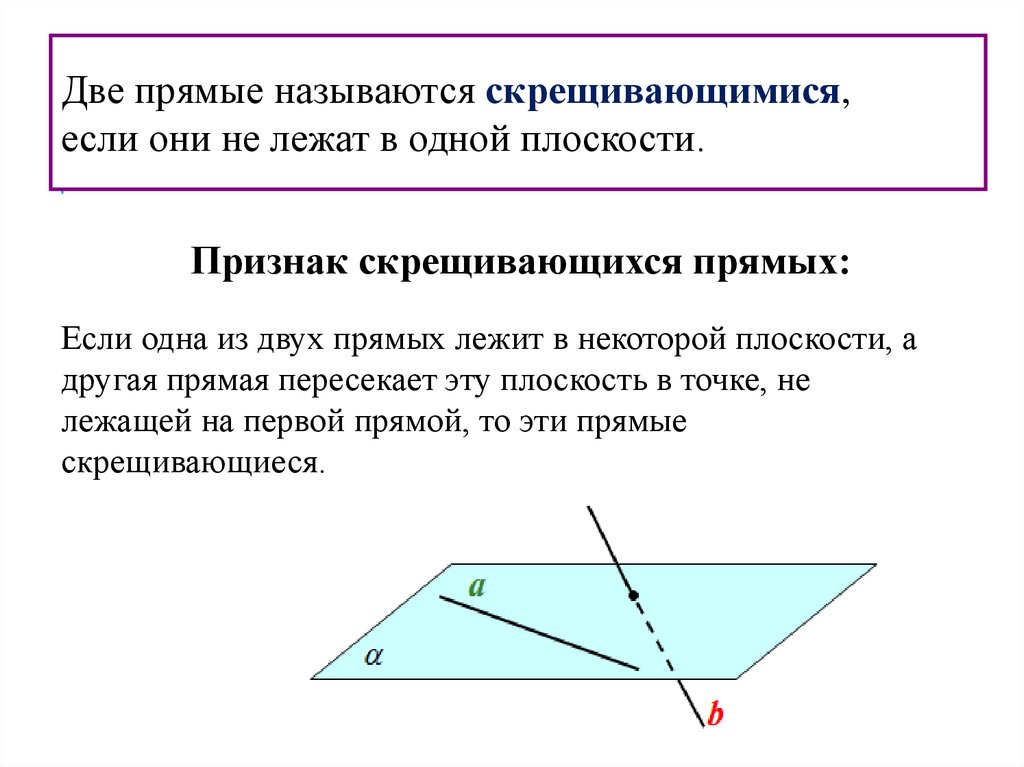
Две прямые называются скрещивающимися,
если они не лежат в одной плоскости.
Признак скрещивающихся прямых:
Если одна из двух прямых лежит в некоторой плоскости, а
другая прямая пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти прямые
скрещивающиеся.

18.

КАК УЗНАТЬ, ЯВЛЯЮТСЯ ЛИ ДВЕ
ПРЯМЫЕ СКРЕЩИВАЮЩИМИСЯ?
• найти плоскость, в которой лежит одна из
этих прямых, а вторая пересекает эту
плоскость, но при этом в точке, не лежащей на
первой прямой;
• надо знать, что они не параллельны, но
могут быть расположены в двух параллельных
плоскостях.

19.

20.

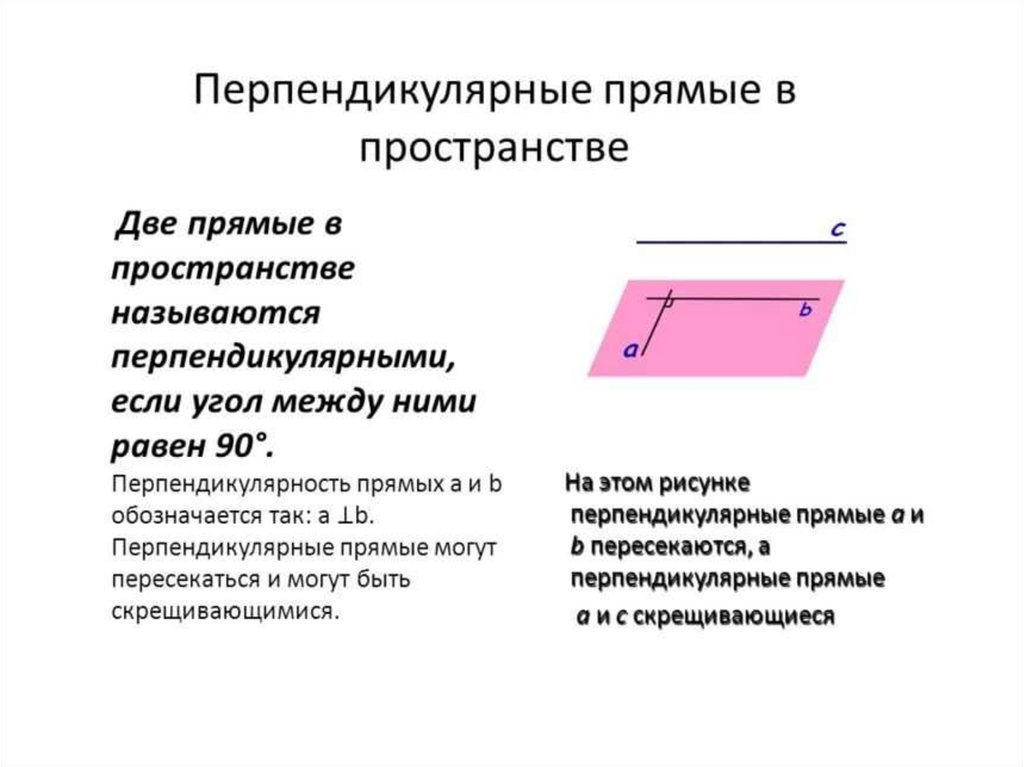
ПЕРПЕНДИКУЛЯРНОСТЬ
ПРЯМОЙ И ПЛОСКОСТИ
Прямая называется перпендикулярной к плоскости,
если она перпендикулярна к любой прямой, лежащей
в этой плоскости.

21.

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМОЙ И ПЛОСКОСТИ
Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в плоскости,
то она перпендикулярна к этой плоскости.

22.

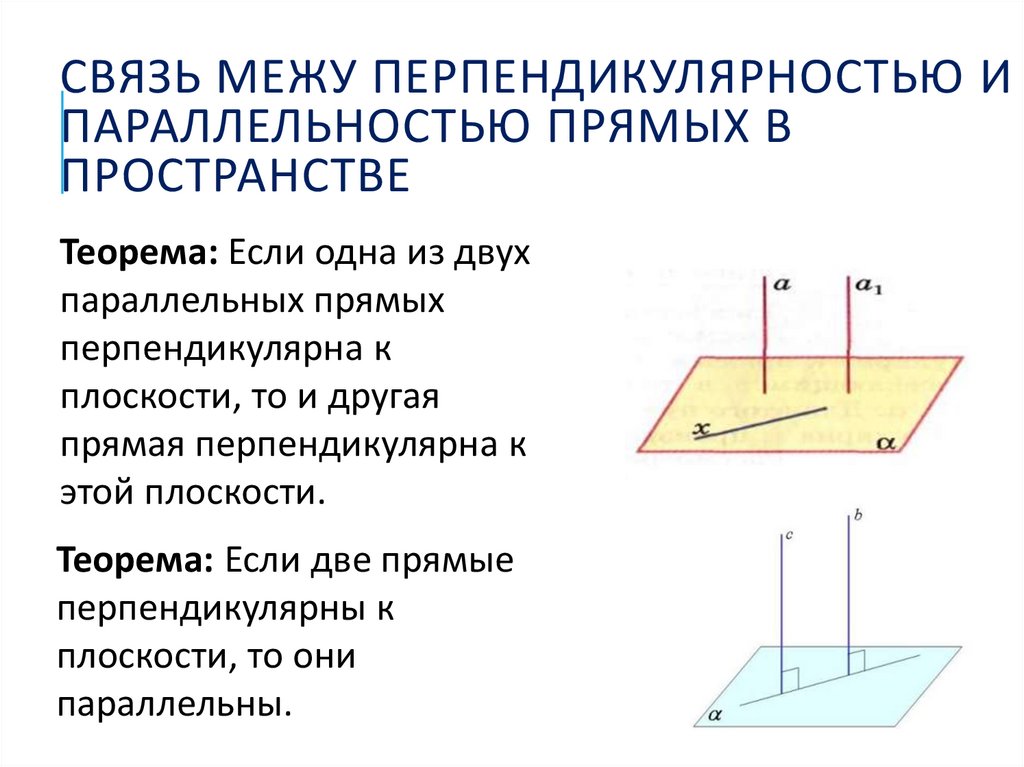
СВЯЗЬ МЕЖУ ПЕРПЕНДИКУЛЯРНОСТЬЮ И
ПАРАЛЛЕЛЬНОСТЬЮ ПРЯМЫХ В
ПРОСТРАНСТВЕ
Теорема: Если одна из двух
параллельных прямых
перпендикулярна к
плоскости, то и другая
прямая перпендикулярна к
этой плоскости.
Теорема: Если две прямые
перпендикулярны к
плоскости, то они
параллельны.

23.

ПРОЕКЦИИ И НАКЛОННЫЕ
Наклонная – это линия, которая не перпендикулярна
плоскости или оси, а имеет определенный угол
наклона к горизонту. Такая линия может двигаться
вверх или вниз, формируя разные углы с горизонтом.
Проекция наклонной – это
представление наклонной
линии на плоскости.

24.

СВОЙСТВА НАКЛОННЫХ И
ПРОЕКЦИЙ
Если из одной точки к плоскости проведены
перпендикуляр и наклонные, то
• Любая наклонная больше перпендикуляра.
• Равные наклонные имеют равные проекции.
• Если проекции наклонных равны, то равны и
наклонные.
• Большей наклонной
соответствует большая проекция
и наоборот.

25.

УГОЛ МЕЖДУ ПРЯМОЙ И
ПЛОСКОСТЬЮ

26.

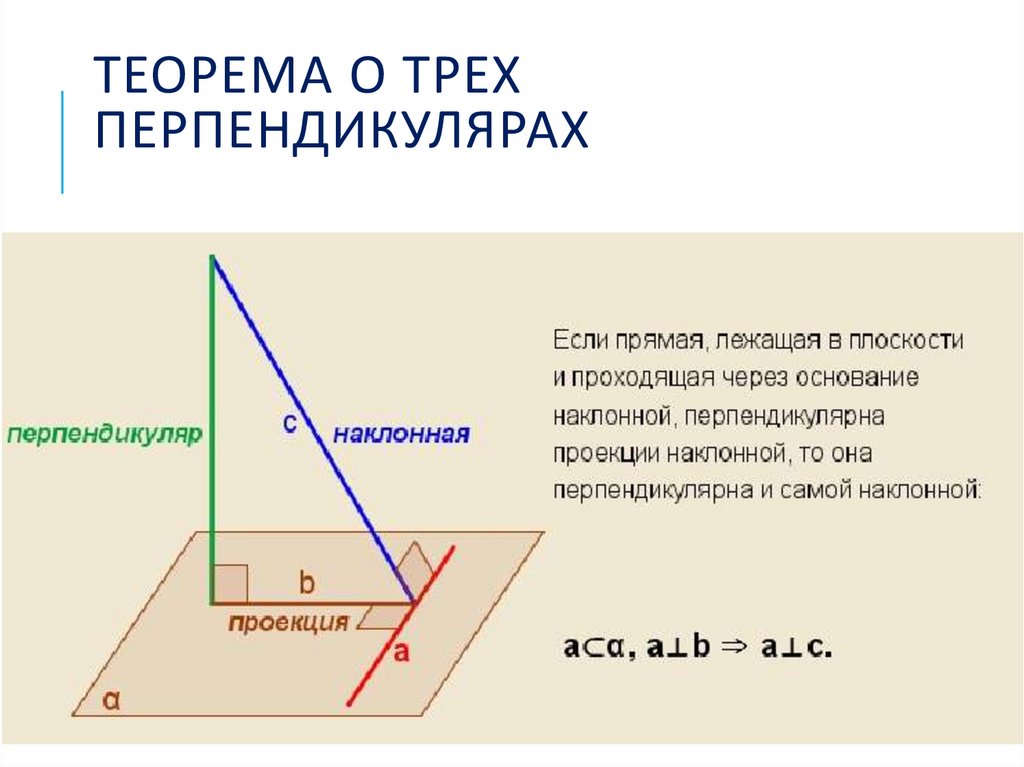
ТЕОРЕМА О ТРЕХ
ПЕРПЕНДИКУЛЯРАХ

27.

ОБРАТНАЯ ТЕОРЕМА
Прямая, проведенная в плоскости через
основание наклонной перпендикулярно к
ней, перпендикулярна и к её проекции.

28.

ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ.
ДВУГРАННЫЙ УГОЛ
Двугранным углом называется фигура,
образованная двумя полуплоскостями с общей
границей.

29.

30.

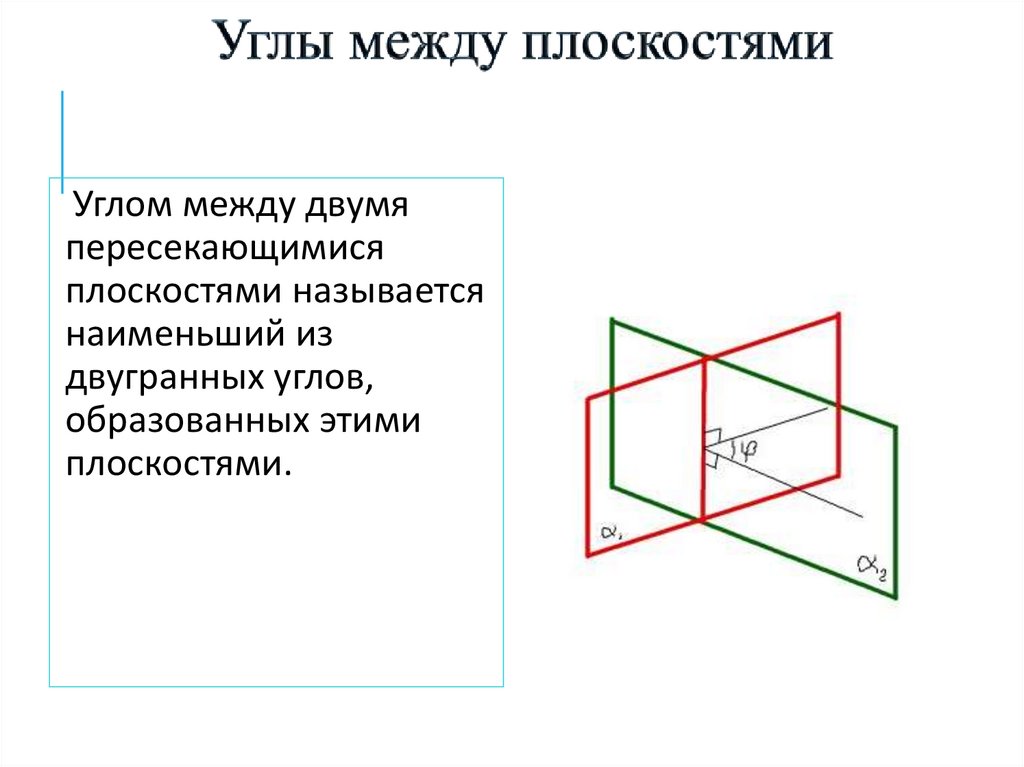
Углом между двумя
пересекающимися
плоскостями называется
наименьший из
двугранных углов,
образованных этими
плоскостями.

31.

ПЕРПЕНДИКУЛЯРНОСТЬ
ПЛОСКОСТЕЙ
Две плоскости называются перпендикулярными, если
они пересекаются под прямым углом.
Признак перпендикулярности плоскостей: Если одна
из двух плоскостей проходит через прямую,
перпендикулярную другой плоскости, то такие
плоскости перпендикулярны.

32.

СВОЙСТВО
ПЕРПЕНДИКУЛЯРНЫХ
ПЛОСКОСТЕЙ
Плоскость, перпендикулярная прямой, по которой
пересекаются две плоскости, перпендикулярна
каждой из этих плоскостей.