Similar presentations:
Энергия светового поля. Поток энергии в световой волне. Интенсивность света
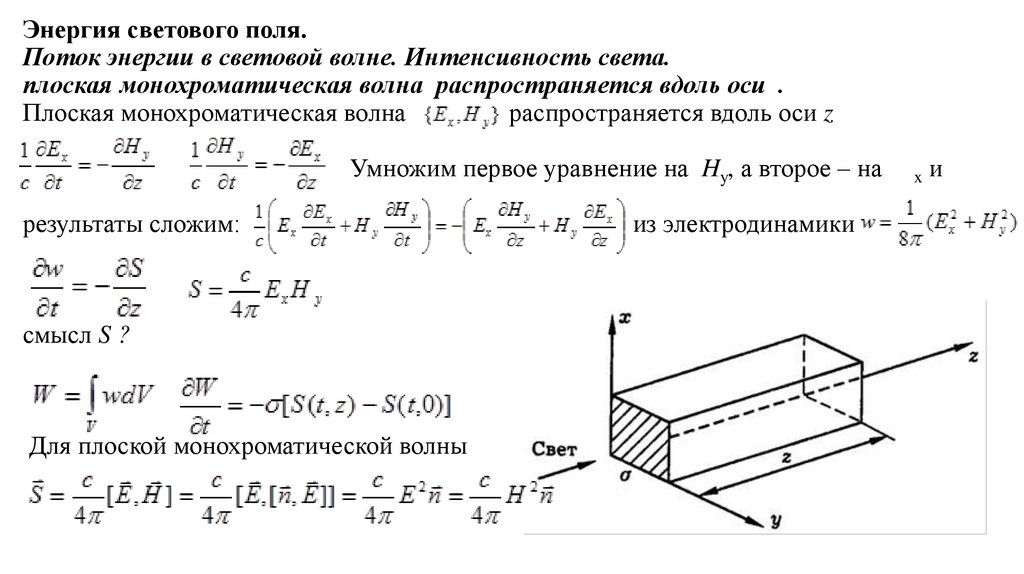
1. Энергия светового поля. Поток энергии в световой волне. Интенсивность света. плоская монохроматическая волна распространяется вдоль оси .
Энергия светового поля.Поток энергии в световой волне. Интенсивность света.
плоская монохроматическая волна распространяется вдоль оси .
Плоская монохроматическая волна
распространяется вдоль оси z
Умножим первое уравнение на Hy, а второе – на
результаты сложим:
смысл S ?
Для плоской монохроматической волны
из электродинамики
x
и
2. Интенсивность света. Для плоской монохроматической волны вида бегущую вдоль оси z модуль вектора Пойнтинга равен Важнейший результат: пот
Интенсивность света.Для плоской монохроматической волны вида
бегущую вдоль оси z
модуль вектора Пойнтинга равен
Важнейший результат: поток энергии содержит два слагаемых – постоянный и
быстро осциллирующий (на удвоенной оптической частоте). Так как измерительные
приборы не могут отслеживать столь быстрые изменения (в оптике - ), то реально
измеримой величиной во всех оптических экспериментах является усредненная по
большому (по сравнению с периодом оптических колебаний ) промежутку времени
величина модуля вектора Пойнтинга:
τ- некоторая временная постоянная, характеризующая фотоприемное устройство,
I – интенсивность света
3. Для плоской монохроматической волны в вакууме Для комплексной записи можно получит аналогичное выражение Энергия, мощность, интенсивност
Для плоской монохроматической волны в вакуумеДля комплексной записи можно получит аналогичное выражение
Энергия, мощность, интенсивность световых пучков и импульсов.
Реальные световые пучки ограничены как в пространстве, так и во времени.
Квазиплоская волна описывается выражением
а световой импульс
Интенсивности световых пучков для данных случаев получим, подставив значение поля
в формулу для интенсивности
Полная мощность определяется интегрированием по поперечному сечению пучка:
4. Реально измеримыми величинами являются параметры мощности и энергии . Измерения проводятся устройствами, называемыми фотоприемниками. Эт
Реально измеримыми величинами являются параметры мощности и энергии . Измеренияпроводятся устройствами, называемыми фотоприемниками. Эти устройства используют
различные физические эффекты (фотоэффект, тепловое действие света и др.) для
преобразования параметров светового пучка в пропорциональную электрическую величину –
напряжение/ток. Величина интервала времени, по которому производится усреднение может
колебаться в широких пределах от 1 до 10-9 с.
Основные понятия фотометрии.
Для описания энергетических характеристик света, испускаемого не лазерными источниками,
пользуются фотометрическими величинами. Сначала рассмотрим так называемые
энергетические единицы измерения этих самых величин, ибо в настоящее время они наиболее
широко распространены. Вводятся следующие понятия:
Поток излучения:
W- энергия, переносимая светом через некоторую поверхность.
Внимание! dt - есть малый промежуток времени, но не бесконечно малая в математическом
смысле. Интервал dt велик по сравнению с периодом колебаний световой волны.
Сила излучения/ энергетическая сила излучения:
где - Ω телесный угол, в котором распространяется поток излучения dФ.
Энергетическая освещенность поверхности:
где: dS - площадь элемента поверхности, облучаемая потоком dФ.
Энергетическая светимость:
где dS - площадь элемента излучающей поверхности.
5. Энергетическая яркость: dS - площадь элемента поверхности источника, θ - угол между нормалью к светящейся поверхности и направлением наблюд
Энергетическая яркость:dS - площадь элемента поверхности источника, θ - угол между нормалью к светящейся
поверхности и направлением наблюдения.
Источники, для которых яркость не зависит от направления излучения, подчиняются
закону Ламберта и называются ламбертовскими источниками.
Излучение традиционных источников света немонохроматично, поэтому приходится
говорить о спектральном разложении фотометрических величин по длинам волн/
частотам. Например, для силы излучения
подинтегральные выражения
спектральных интервалах
, имеют смысл потока излучения в
, соответственно.
6. Функция видности С помощью данной кривой легко вычислить соотношение для любой длины волны в пределах видимого диапазона. Для немонохрома
Функция видностиС помощью данной кривой легко вычислить соотношение для любой длины волны в
пределах видимого диапазона. Для немонохроматического света
7. Сферическая волна. Решением волнового уравнения являются волны вида для которых напряженность поля зависит только от Такие волны называю
Сферическая волна.Решением волнового уравнения являются волны вида
для которых напряженность поля зависит только от
Такие волны называются сферическими.
Рассмотрим скалярное волновое уравнение для
введем замену переменной
получим
или
E0
E (r , t )
exp(i ( t k r ))
r








 physics
physics








