Механика. Тема 3. Всемирное тяготение

1.

Механика
Тема 3
Всемирное тяготение
2022 г.

2.

Законы Кеплера

3.

Законы Кеплера

4.

Законы Кеплера
Геоцентрическая система
мира (ок. 90 – ок. 160 н.э.),
К. Птолемей
Галилео Галилей
(1564–1642)
Гелиоцентрическая
система мира (1539),
Н. Коперник
Тихо Браге
(1546-1601)
Иоганн Кеплер
(1571-1630)

5.

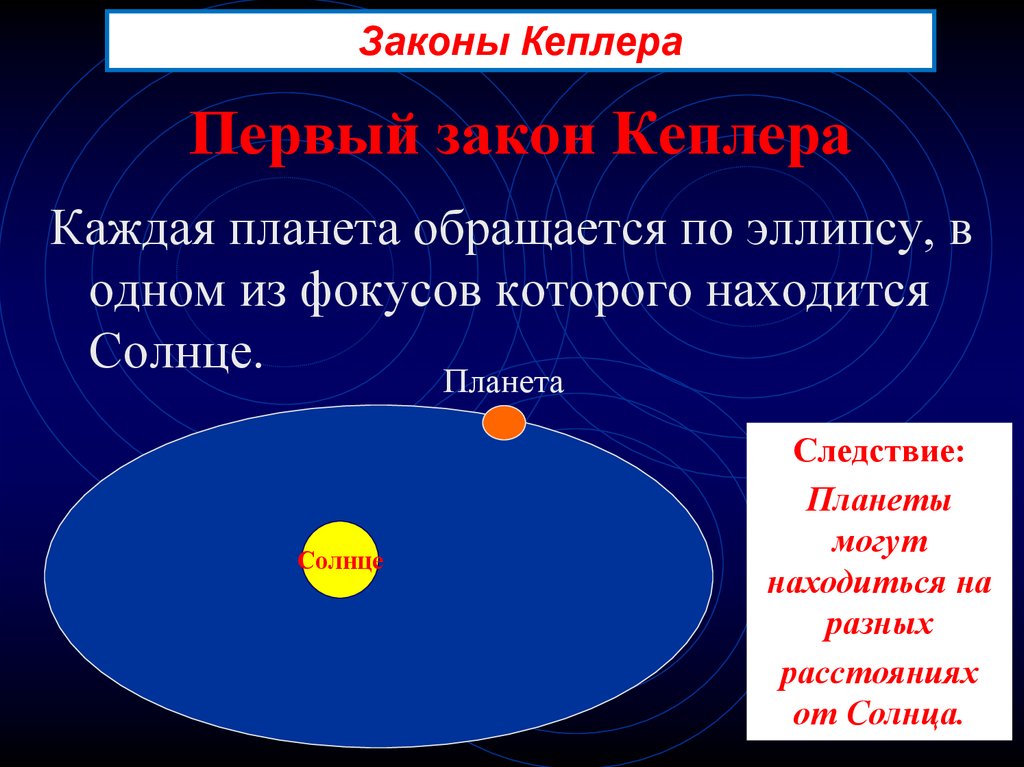
Законы Кеплера
Первый закон Кеплера
Каждая планета обращается по эллипсу, в
одном из фокусов которого находится
Солнце.
Планета
Солнце
Следствие:
Планеты
могут
находиться на
разных
расстояниях
от Солнца.

6.

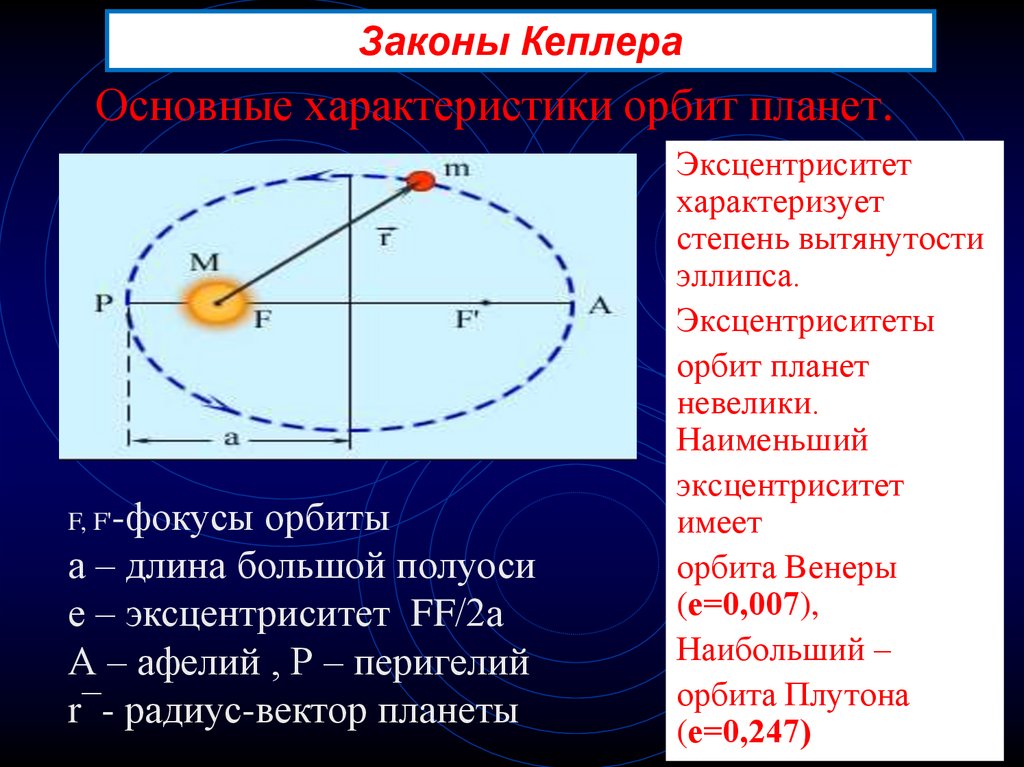
Законы Кеплера
Основные характеристики орбит планет.
F, F'-фокусы орбиты
а – длина большой полуоси
е – эксцентриситет FF/2а
А – афелий , Р – перигелий
r¯- радиус-вектор планеты
Эксцентриситет
характеризует
степень вытянутости
эллипса.
Эксцентриситеты
орбит планет
невелики.
Наименьший
эксцентриситет
имеет
орбита Венеры
(е=0,007),
Наибольший –
орбита Плутона
(е=0,247)

7.

Законы Кеплера
Второй закон Кеплера
Радиус-вектор планеты описывает за
равные промежутки времени равные
площади.
Следствие:
Планеты по орбите
движутся не
равномерно:
В перигелии
скорость планеты
наибольшая,
в афелии наименьшая.

8.

Законы Кеплера
Третий закон Кеплера
Квадраты периодов обращения планет
относятся как кубы больших полуосей их
орбит.
2
1
2
2
T
T
3
1
3
2
a
a
Следствие:
Чем дальше находится
планета от Солнца,
тем больше её
период обращения.
Меркурий
88
суток, Плутон - 249
лет

9.

Закон всемирного тяготения
На склоне своих дней Исаак Ньютон рассказал, что
примерно в 1665 году ему и пришло в голову, что, возможно,
это одна и та же сила заставляет и яблоко падать на землю, и
Луну оставаться на околоземной орбите. В последующие годы
Ньютон пытался найти физическое объяснение законам движения
планет открытых астрономом И. Кеплером, и дать
количественное выражение для гравитационных сил. Зная как
движутся планеты, Ньютон хотел определить, какие силы на них
действуют. Такой путь носит название обратной задачи механики.
Если основной задачей механики является определение
координат тела и его скорости в любой момент времени по
известным силам, действующим на тело (прямая задача
механики), то при решении обратной задачи необходимо
определить действующие на тело силы, если известно, как оно
движется. Решение этой задачи и привело Ньютона к открытию
закона всемирного тяготения. Это был примерно 1682 год.
Классическая формулировка закона всемирного тяготения была
дана И. Ньютоном в 1687 году в его труде «Математические
начала натуральной философии».

10.

Закон всемирного тяготения
m1 m 2
F =G 2
r
Ньютон предположил, что сила тяжести меняется обратно
пропорционально квадрату расстояния. Тогда Луна,
находящаяся от Земли на расстоянии примерно 60 ее
радиусов, должна испытывать ускорение в 3600 раз меньшее,
чем ускорение силы тяжести на поверхности Земли, равное
9,8 м/с2 .
Следовательно, ускорение Луны должно составлять 0,0027
м/с2.
В то же время Луна, как любое тело, равномерно движущееся
по окружности, имеет ускорение
радиус Земли равен 6400 км, и радиус лунной орбиты будет составлять
r = 60 • 6 400 000 м (3,84 • 106 м). Период обращения Луны Т = 27,32 суток (2,36
106 с). Тогда ускорение орбитального движения Луны
Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну
на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с
действующей на поверхности Земли.

11.

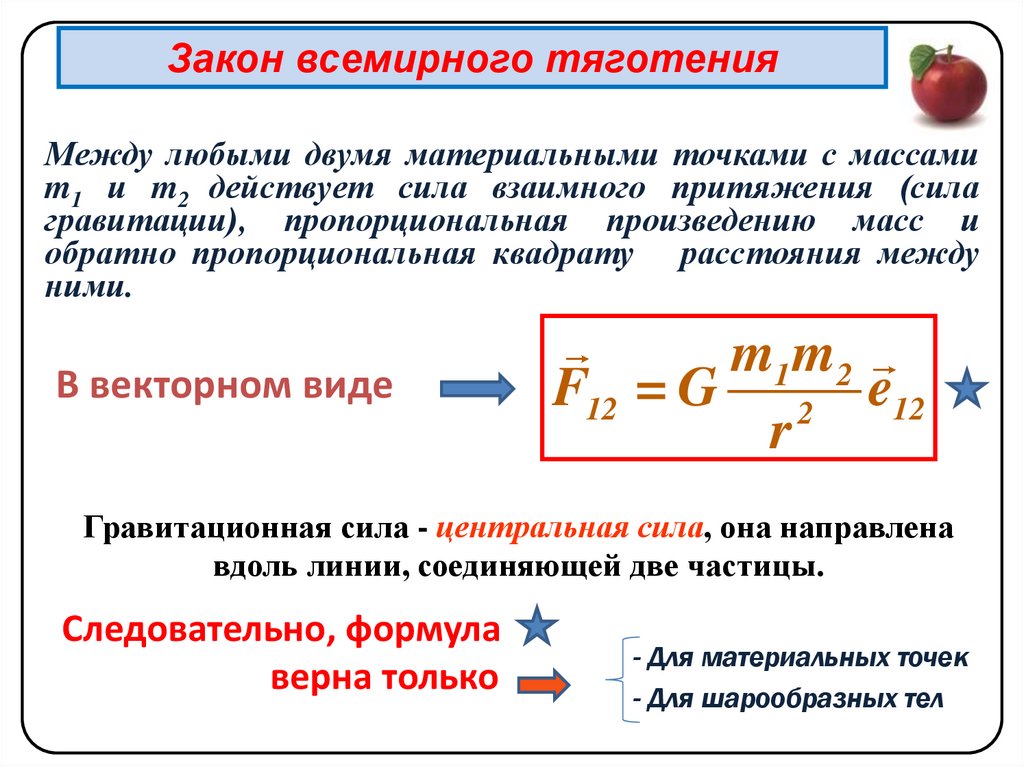
Закон всемирного тяготения
Между любыми двумя материальными точками с массами
m1 и m2 действует сила взаимного притяжения (сила
гравитации), пропорциональная произведению масс и
обратно пропорциональная квадрату расстояния между
ними.
В векторном виде
m1 m 2
F12 = G 2 e12
r
Гравитационная сила - центральная сила, она направлена
вдоль линии, соединяющей две частицы.
Следовательно, формула
верна только
- Для материальных точек
- Для шарообразных тел

12.

Закон всемирного тяготения
Для нахождения гравитационной
силы притяжения между
протяженными телами надо
каждое из тел разбить на малые
массы и просуммировать силы
притяжения между всеми парами
таких масс в двух телах
mi
1
F ik
eik
F ki
2 mk
Δmi Δmk
F12 = Fik = G
eik
2
rik
i
k
i
k
В пределе при Δmi , Δmk 0
двойная сумма переходит в двойной
интеграл, взятый по объемам двух тел.

13.

Закон всемирного тяготения

14.

Гравитационная постоянная (G)
В 1686 г. Ньютон сформулировал закон всемирного тяготения
и ввёл при этом G как коэффициент пропорциональности. Он
смог только оценить величину G. Точное ее измерение сильно
затруднено, – т.к. силы тяготения очень малы.
Впервые измерил G Генри Кавендиш в 1797 г..
Крутильные весы
(Дж. Мичелл, 1783)
1 – коромысло,
2 – нить,
3 – шкала,
4 – луч света,
5 – зеркальце.
Генри Кавендиш (1731-1810)
– сын герцога Девоншира и
герцогини Грей (Кента)

15.

Гравитационная постоянная (G)

16.

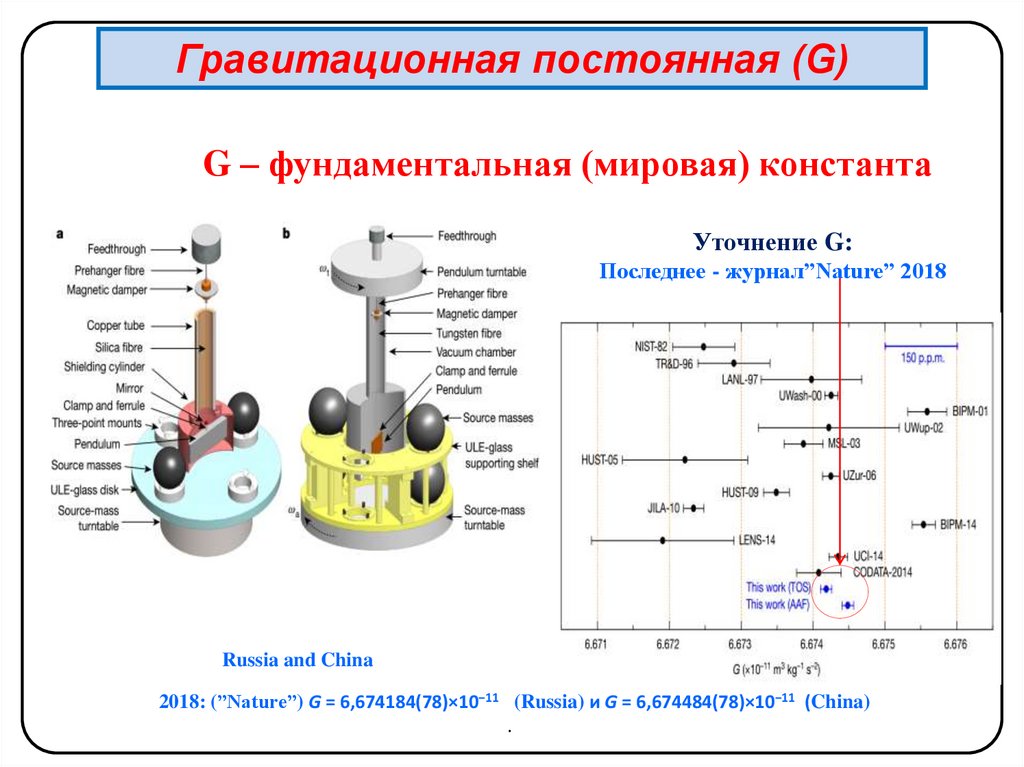
Гравитационная постоянная (G)
G – фундаментальная (мировая) константа
Уточнение G:
Последнее - журнал”Nature” 2018
Russia and China
2018: (”Nature”) G = 6,674184(78)×10−11 (Russia) и G = 6,674484(78)×10−11 (China)
.

17.

Масса инертная и масса гравитационная
Понятие «масса» фигурирует в двух
разных законах: во втором законе Ньютона и в
законе всемирного тяготения.
Fk
k
a
m
m1 m 2
F12 = G 2 e12
r
В первом случае она характеризует инертные
свойства тела, во втором гравитационные свойства,
то есть способность тел притягиваться друг к другу.
В связи с этим возникает вопрос: не следует ли
различать инертную массу mин
и массу
гравитационную (или тяготеющую) mg?

18.

Масса инертная и масса гравитационная
mин = mg ??
1867 г. Ньютон доказал это равенство с
точностью до 10-3.
1901 г. венгерский физик Этвеш получил такое
совпадение с точностью до 10-8.
1964 г. американский ученый Дикке улучшил
точность измерения в 300 раз.
Тождественность инертной и
гравитационной масс Эйнштейн положил в
основу общей теории относительности.

19.

Масса инертная и масса гравитационная
- Тождественность инерциальной и гравитационной масс
является следствием эквивалентности сил инерции и сил
тяготения.
- Этот факт называется принципом эквивалентности
Эйнштейна.
Согласно этому принципу, все физические процессы в
истинном поле тяготения и в ускоренной системе
отсчета, в отсутствии тяготения, протекают
одинаковым образом.
Этот фундаментальный закон природы – постулат общей
теории относительности.
Следствием этого закона является то, что находясь внутри
закрытой кабины, невозможно определить, чем вызвана
сила mg, тем, что кабина движется с ускорением или
действием притяжения Земли.

20.

Закон всемирного тяготения
Изменения ускорения свободного падения g
Ускорение свободного падения
на Земле зависит от:
1. высоты над Землёй;
2. различия пород земной коры;
3. географической широты;
4. формы Земли.

21.

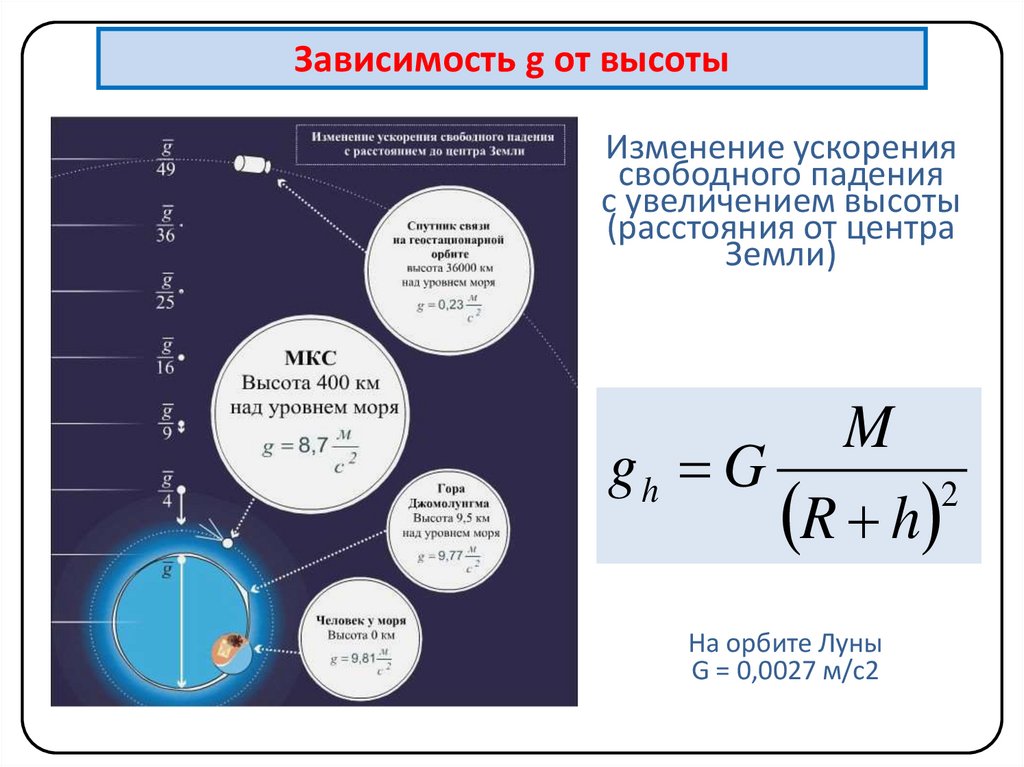
Зависимость g от высоты
Изменение ускорения
свободного падения
с увеличением высоты
(расстояния от центра
Земли)
M
gh G
2
R h
На орбите Луны
G = 0,0027 м/с2

22.

Зависимость g от различия пород земной коры
- Земля является шаром с неоднородной плотностью