Выборочное наблюдение

5.33M

Category: $mathematics$ mathematics

Выборочное наблюдение - вид несплошного
наблюдения, при котором признаки регистрируются у
отдельных единиц изучаемой совокупности, отобранных
с использованием специальных методов.
Вся совокупность единиц, из которой осуществляется
отбор, называется генеральной совокупностью, а
единицы, отобранные для непосредственного наблюдения, представляют собой выборочную
совокупность, или просто выборку.
2

3.

• При выборочном методе обследованию
подвергается сравнительно небольшая
часть всей изучаемой совокупности
(обычно до 5–10 %, реже до 15–25 %).
• При организации выборочного
обследования нужно соблюдать принцип
случайности отбора.
3

4.

Основные преимущества выборочного
наблюдения:
• экономия трудовых затрат и средств на
получение и обработку информации
• быстрота проведения наблюдения;
• лучшая организация наблюдения;
4

5.

Виды выборок
1)По степени охвата единиц совокупности:
•
большая выборка;
•
малая выборка.
2)По способам отбора единиц из генеральной
совокупности:
•
возвратная выборка (повторная)
• бесповторная выборка
5

6.

3) По способу формирования выборочной
совокупности:
• простая случайная,
• механическая,
• расслоенная (типическая),
• серийная,
• комбинированная
6

7.

Основные показатели выборочного наблюдения
Генеральная совокупность
N - Объем генеральной совокупности
(общее число исследуемых единиц)
Выборочная совокупность
n - Объем выборки (число
обследованных единиц)
7

8.

Генеральная совокупность
Выборочная совокупность
Дисперсия
генеральная дисперсия (дисперсия
выборочная дисперсия
признака в генеральной совокупности)
x2
2
(
x
x
)
i
N
Среднее квадратическое отклонение
среднее квадратическое отклонение в среднее квадратическое
генеральной совокупности
отклонение в выборке
x
2
(
x
x
)
i
N
8

9.

Для АЛЬТЕРНАТИВНОГО признака
Генеральная совокупность
Выборочная совокупность
Дисперсия ДОЛИ
генеральная дисперсия (дисперсия
выборочная дисперсия
признака в генеральной совокупности)
p2 p q p (1 p)
Среднее квадратическое отклонение ДОЛИ
среднее квадратическое отклонение в среднее квадратическое
генеральной совокупности
отклонение в выборке
p p q
9

10.

Альтернативный признак - наличие или отсутствии изучаемого
свойства у единицы совокупности.
Пример: цвет детали - красный
Вариация альтернативного признака выражается двумя значениями:
1) наличие у единицы изучаемой совокупности некоторого свойства
обозначается единицей 1;
2) отсутствие свойства обозначается нулем 0.
Доля единиц:
1) обладающих изучаемым признаком обозначается p,
2) не обладающих этим признаком обозначается q.
p+q=1
отсюда q = 1 — p
10

11.

Альтернативный признак
1) Среднее значение признака:
1 p 0 q p
x
p
p q
1
2) Дисперсия:
2
2
2
2
(
1
p
)
p
(
0
p
)
q
q
p
p
q p q( q p )
2
p q
p q
p q
p q
3) Среднее квадратическое отклонение:
p q
Пример: в изготовленной партии деталей 3% изделий оказались
бракованными. Найти среднее значение и среднее квадратическое
отклонение бракованных деталей.
x 0,03
0,03 0,97 0,1706 17,06%
11

12.

Ошибки репрезентативности – расхождение между
показателями в генеральной и выборочной
совокупностях
• Систематические ошибки связаны с
нарушением принципов формирования
выборочной совокупности.
• Случайные ошибки репрезентативности связаны
с невозможностью полностью воспроизвести все
характеристики генеральной совокупности в
выборочной совокупности.
12

13.

Оценка случайных ошибок — одна из задач
статистики.
Ошибка выборки (ошибка
репрезентативности) представляет собой
разность соответствующих выборочных и
генеральных характеристик:
• Ошибка средней величины e~x ~x x
• Ошибка доли ep w p
13

14.

Величина ошибки выборки зависит от:
• степени вариации изучаемого признака,
• численности выборки и
• метода отбора единиц в выборочную
совокупность.
14

15.

Различают среднюю и предельную ошибки выборки.
Эти две вида ошибок связаны соотношением:
= t∙
• - предельная (максимально возможная) ошибка
выборки
• - величина средней квадратической стандартной
ошибки (стандартная или средняя ошибка)
• t – коэффициент кратности средней ошибки выборки,
зависящей от вероятности, с которой гарантируется
величина предельной ошибки
Величина средней ошибки выборки рассчитывается в
зависимости от вида выборки
15

16. Простая случайная выборка

При простой случайной выборке отбор единиц в
выборочную совокупность производится
непосредственно из всей массы единиц
генеральной совокупности в форме случайного
отбора.
Случайный отбор может осуществляется путем
применения жеребьевки (лотереи) или путем
использования таблиц случайных чисел.
16

17.

Случайный отбор может быть проведен:
• в форме возвратной (повторной) выборки
вероятность попадания каждой единицы генеральной
совокупности остается постоянной, так как после отбора
какой-то единицы она снова возвращается в генеральную
совокупность и может быть выбранной
• в форме безвозвратной (бесповторной)
выборки.
выбранная единица не возвращается в генеральную
совокупность и вероятность попадания отдельных единиц
в выборку все время изменяется (для оставшихся единиц
она возрастает).
17

18.

На основе выборочных данных делается
вывод о характеристиках генеральной
совокупности:
• по выборочной средней определяется
генеральная средняя
или
• на основе выборочного наблюдения
определяется доля единиц, обладающих
данным признаком в генеральной
совокупности.
18

19.

20.

21.

Способ отбора единиц
Повторный
Безповторный
Средняя
ошибка для
средней
Средняя
ошибка для
доли
21

22.

Средняя и предельная ошибки выборки связаны
соотношением:
= t∙
Способ отбора единиц
Повторный
Безповторный
Предельная
ошибка для
средней
Предельная
ошибка для
доли
22

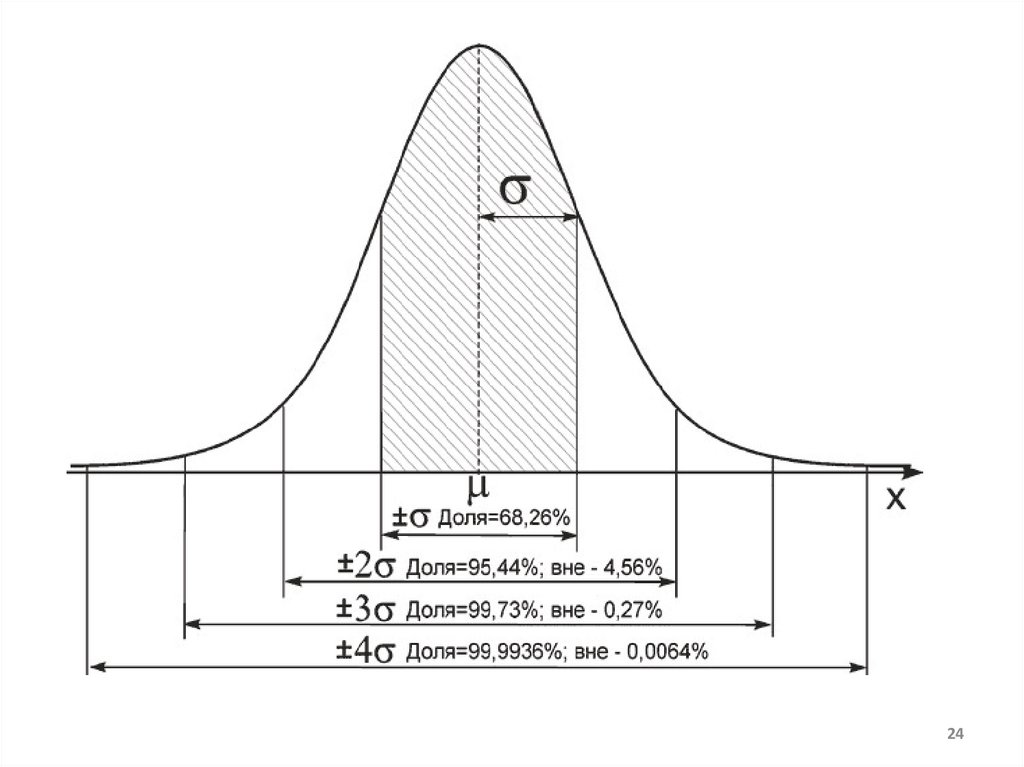
23.

t - коэффициент доверия, который определяется по
таблице значений интегральной функции Лапласа при
заданной доверительной вероятности P.
Наиболее часто употребляемые уровни
доверительной вероятности и соответствующие им
значения :
P(t)
t
0,683
1,00
0,950
1,96
0,954
2,00
0,990
2,58
0,997
3,00
23

24.

25. 26. Определение необходимого объема выборки

27.

• В случае простой случайной выборки
необходимая численность выборки
определяется по следующим формулам:
Численность
выборки
Для определения
среднего размера
выборки
Для определения
доли признака
Способ отбора единиц
Повторный
Безповторный
27

28.

Пример. На предприятии в порядке случайной бесповторной выборки
было опрошено 100 рабочих из 1000 и получены следующие данные об
их доходе за месяц.
Месячный доход,
тыс. руб.
чел
6-10
10-14
14-18
18-22
12
60
20
8
Определить:
1. среднемесячный размер дохода у работников данного предприятия,
гарантируя результат с вероятностью 0,997;
2. долю рабочих предприятия, имеющих месячный доход 14тыс. руб. и
выше, гарантируя результат с вероятностью 0,954;
3. необходимую численность выборки при определении среднего
месячного дохода работников предприятия, чтобы с вероятностью
0,954 предельная ошибка выборки не превышала 0,5 тыс. руб.;
4. необходимую численность выборки при определении доли рабочих
с размером месячного дохода 14,0 руб. и выше, чтобы с
вероятностью 0,954 предельная ошибка не превышала 4%.
28

29.

Месячный доход,
тыс. руб.
6-10
12
10-14
60
14-18
20
18-22
8
29

30.

Месячный доход,
тыс. руб.
6-10
12
10-14
60
14-18
20
18-22
8
30

31.

Месячный доход,
тыс. руб.
6-10
12
10-14
60
14-18
20
18-22
8
31

32.

Месячный доход,
тыс. руб.
6-10
12
10-14
60
14-18
20
18-22
8
32

33.

Месячный доход,
тыс. руб.
6-10
12
10-14
60
14-18
20
18-22
8
33

34.

Месячный доход,
тыс. руб.
6-10
12
10-14
60
14-18
20
18-22
8
34

35. Механическая выборка

Основана на предварительном упорядочении генеральной
совокупности (по алфавиту, в пространстве,
последовательности появления во времени).
• Устанавливается процент отбора, исходя из которого
определяется число отбираемых единиц.
• Отбор единиц в выборочную совокупность производится
из генеральной совокупности через равные промежутки
(интервалы): определяется начало отбора, т.е. номер
первой обследуемой единицы; каждая следующая
единица включается в выборку в соответствии с
установленным шагом отбора.
35

36.

При организации механического отбора
необходимо:
а) Определить шаг отчета
б) Выбрать единицу, с которой надо начинать
отсчет
• Определить «шаг» отчета можно по формуле N/n
Так, при 2 %-ной выборке отбирается каждая 50-я единица (1 : 0,02), при
5 %-ной выборке — каждая 20-я единица (1 : 0,0)
• Выбор единицы отсчета рекомендуется
производить путем случайного отбора из единиц
первого интервала.
36

37.

• Таким образом, в соответствии с принятой
долей отбора генеральная совокупность
как бы механически разбивается на равные
группы. Из каждой группы в выборку
отбирается лишь одна единица.
• На практике часто используют фактический
порядок, в котором размещаются единицы
генеральной совокупности (например,
последовательность выхода готовых
изделий с конвейера).
37

38.

Ошибка выборки при использовании механической
выборки оценивается с помощью формул для
случайной бесповторной выборки.
Средняя ошибка для
средней
Средняя ошибка для
доли
Предельная ошибка для
средней
Предельная ошибка для
доли
38

39. Типическая выборка

Если генеральная совокупность представлена крупными
группами (районами), средние значения в которых сильно
различаются, рекомендуется использовать метод типической
выборки
• В выборочную совокупность производится отбор единиц
из каждой такой типической группы случайно или
механически.
• В результате обеспечивается более равномерное
представительство в выборочной совокупности различных
групп.
• ni - число единиц, попавших в выборку из i-й группы,
• m - общее число образованных групп.
39

40.

Число единиц в каждой группе можно
определить одним из трех способов:
1) отбор из каждой группы равного числа
единиц, т.е. ni = n/m.
• Использование такого принципа отбора
позволяет получить достаточно надежные
результаты лишь при равных размерах
выделенных типических групп.
• Если же их численность существенно различается
между собой, то использование равномерного
отбора может привести к смещению оценок,
полученных по результатам выборочного
обследования;
40

41.

42.

43.

Расчет ошибки выборки при
пропорциональном распределение единиц
выборочной совокупности по группам
Способ отбора единиц
Повторный
Безповторный
Средняя
Доля
43

44.

Расчет ошибки выборки при оптимальном
распределение единиц выборочной
совокупности по группам
Способ отбора единиц
Повторный
Безповторный
Средняя
Доля
44

45.

• Важной особенностью типической выборки
является то, что она дает более точные
результаты по сравнению с другими
способами отбора единиц в выборочную
совокупность.
• Но ее преимущества проявляются только
при условии, что различия в средних
значениях изучаемого признака между
группами достаточно ощутимы, а вариация
признака внутри каждой группы невелика.
45

46.

Пример. Для изучения объема и структуры доходов
работников городских торговых предприятий, относящихся к
разным формам собственности, проведен 2-процентный
бесповторный типический отбор. Отбор проведен
пропорционально численности работников, занятых на
предприятиях каждой выделенной группы
Результаты по одному из обследованных показателей
приведены в таблице
Форма
собственности
Числен Обсле
Доход от участия в собственности
ность довано предприятия на одного работника в год,
занятых, человек
тыс. руб.
среднее квадратичел.
средний
ческое отклонение
Государственная 5000
Негосударственн 25000
ая
Всего
30000
100
500
270
880
90
260
600
46

47.

Форма
собственности
Числен Обсле
Доход от участия в собственности
ность довано предприятия на одного работника в год,
занятых, человек
тыс. руб.
среднее квадратичел.
средний
ческое отклонение
Государственная 5000
Негосударственн 25000
ая
Всего
30000
100
500
270
880
90
260
600
47

48.

Форма
собственности
Государственная 5000
Негосударственн 25000
ая
Всего
30000
100
500
270
880
90
260
600
48

49.

Форма
собственности
Государственная 5000
Негосударственн 25000
ая
Всего
30000
100
500
270
880
90
260
600
49

50.

Форма
собственности
Государственная 5000
Негосударственн 25000
ая
Всего
30000
100
500
270
880
90
260
600
50

51. Серийная выборка

• Применяется в том случае, если генеральная
совокупность разбита на группы (серии) еще до начала
выборочного обследования.
• Из генеральной совокупности отбираются не отдельные
единицы, а целые серии.
• Внутри отобранной серии производится сплошное
наблюдение, т.е. рамках каждой серии обследованию
подлежат все попавшие в нее единицы.
• Такой способ отбора широко применяется при контроле
качества продукции, когда для проведения наблюдения
вскрывается упаковка, содержащая определенное количество изделий, и все они проверяются.
51

52.

53.

54.

• Оценка средней ошибки
М – количество серий в генеральной совокупности
Способ отбора единиц
Повторный
Безповторный
Средняя
доля
54

55.

Пример. При контрольной проверке качества деталей
проведена 10%-ная серийная выборка. Из партии,
содержащей 50 ящиков, методом механического отбора
взято 5 ящиков. В результате сплошного обследования
находящихся в ящике деталей получили данные об удельном
весе бракованных деталей.
Номер ящика, попавшего в
выборку
Удельный вес бракованной
продукции, %
1
2
3
4
5
1,2
1,8
2
1
1,5
Требуется с вероятностью 0,95 установить доверительные
интервалы удельного доли бракованной продукции для всей
партии
55

56.

Номер ящика, попавшего в
выборку
Удельный вес бракованной
продукции, %
1
2
3
4
5
1,2
1,8
2
1
1,5
56

57.

Номер ящика, попавшего в
выборку
Удельный вес бракованной
продукции, %
1
2
3
4
5
1,2
1,8
2
1
1,5
57

58. Комбинированная выборка

• Комбинированная выборка предполагает использование
нескольких способов выборки.
• Например, можно комбинировать серийную выборку и
случайную.
• На первом этапе из совокупности отбираются
укрупненные единицы (серии), а затем без проведения
наблюдения за всеми единицами в рамках серии
осуществляется собственно случайный или механический
отбор единиц из каждой отобранной серии.
• Комбинированная выборка может быть повторной (для
групп и единиц) и бесповторной.
58

59. 60. Малая выборка

• Под малой выборкой понимается несплошное
статистическое обследование, при котором выборочная
совокупность образуется из сравнительно небольшого
числа единиц генеральной совокупности. Объем малой
выборки обычно не превышает 30 единиц.
• Обычно применяются в том случае, когда невозможно или
нецелесообразно использовать большую выборку
(исследование качества продукции, если это связано с ее
разрушением, в частности на прочность, на
продолжительность срока службы и т. д.).
60

61.

62.

• Для расчета коэффициента доверия t определяют
S(t) — значение функции Стьюдента
S(t) =(P+ 1) : 2,
где Р — величина доверительной вероятности.
• Затем по таблице распределения Стьюдента в
зависимости от значения функции и числа
степеней v (v = n – 1) определяют значение t.
62

63.

64.

Пример. Из партии электроламп произведена малая
выборка (отбор случайный, бесповторный) для
определения продолжительности службы ламп.
Номер
лампы
Срок
горения, ч
1
2
3
4
5
6
7
8
9
10
1450 1370 1250 1400 1360 1420 1400 1320 1300 1430
На основе приведенных данных требуется:
• определить доверительные интервалы, в которых
заключена средняя продолжительность службы ламп для
всей партии, гарантируя результат с вероятностью 0,99;
• определить вероятность того, что средний срок службы
ламп для всей партии отличается от полученного по
выборке не более чем на 40 ч.
64