Similar presentations:
Струйные насосы. Лекция 10
1.
Струйные насосыКасабеков М.И.
для студентов специальности В056-5403
«Механика-прикладная математика»
Лекция 10
1
24.10.2023
2.
ВведениеСтруйными называют насосы, у
которых приращение энергии
перекачиваемой жидкости происходит
за счет кинетической энергии струи
жидкости того же или другого рода.
Лекция 10
2
24.10.2023
3.
Повестка дняПринцип действия
Процессы в основных элементах
струйного насоса
Основное энергетическое уравнение,
параметры
и
характеристики
жидкостных струйных насосов
Лекция 10
3
24.10.2023
4.
рвВ
р3
III
р1
I
y
z1
x рx
u0
р4
IV
ux
x
I
III
II
II
A
lксм
u3
u1
7
6
5
4
z2
3
2
В
l1
1
ра
A
l2
l3
IV
5.
Принцип действияВ трубопровод 2 в количестве G1, кг/с,
подается капельная или газообразная
рабочая жидкость, которая, вытекая из
сопла 3 со скоростью u0, образует рабочую
струю. Величина кинетической энергии
струи определяется давлением р1 жидкости
в трубопроводе 2. Перекачиваемая жидкость
в количестве G2 по всасывающему
трубопроводу подводится к всасывающему
патрубку 1 струйного насоса и дальше к
сечению III – III, в котором располагается
выходное отверстие сопла и начинается
камера смешения 5.
5
Лекция 10
24.10.2023
6.
Скорость потока перекачиваемой жидкостиu3 в сечении III – III значительно меньше
скорости рабочей струи u0. Совместное
движение этих двух потоков в направлении
оси камеры смешения будет сопровождаться
взаимным трением, вследствие чего
скорость рабочей струи будет уменьшаться,
а перекачиваемой жидкости –
увеличиваться.
7.
В слое, непосредственно окружающемрабочую струю, происходит интенсивный
обмен энергией перекачиваемой и рабочей
жидкости. Кинетическая энергия струи в
продольном и поперечном направлениях
уменьшается, а перекачиваемой жидкости –
увеличивается. Таким образом, при помощи
струи рабочая жидкость непосредственно
передает свою энергию перекачиваемой
жидкости; следовательно, в струйном
насосе «рабочим органом» является струя
рабочей жидкости.
8.
Движение двух рассматриваемых потоковжидкости сопровождается выравниванием
поля скоростей и в некотором сечении х–х
горловины 6, достаточно удаленном от
выходного сечения сопла, завершается
образованием смеси примерно однородной
концентрации. При этом рабочая струя
теряет свою индивидуальность,
существенно деформируется и здесь
заканчивается ее всасывающее действие.
9.
За сечением х–х следует диффузор 7, вкотором происходит преобразование
кинетической энергии получившейся смеси
жидкостей в потенциальную. В результате
этого процесса в выходном сечении
диффузора IV–IV устанавливается величина
скорости, допустимая для движения в
нагнетательном трубопроводе или для
выхода в атмосферу.
10.
Словарь терминовСтруйные насосы работают либо как
эжекторы, либо как инжекторы.
Эжектором называют насос,
приспособленный для выкачивания
жидкости (воздуха, воды, масла и др.).
Для этого всасывающий патрубок насоса присоединяется к
обслуживаемому объекту.
Инжектором называют насос,
накачивающий жидкость под давлением в
резервуар.
В этом случае к обслуживаемому объекту присоединяется
нагнетательный патрубок насоса.
Лекция 10
10
24.10.2023
11.
Процессы в основных элементахструйного насоса
В
сопле водоструйного насоса происходит
преобразование
потенциальной
энергии
в
кинетическую,
что
сопровождается
гидравлическими потерями, величина которых
зависит от формы и качества изготовления сопла.
На рисунке сечением I – I обозначено начало
сопла, в котором устанавливается абсолютное
давление р1 и скорость u1, а сечением III – III
выходное отверстие сопла, где устанавливается
абсолютное
давление
р3.
Допуская,
что
гидравлическое сопротивление сопла может быть
оценено коэффициентом zс=(0,05 – 0,1), найдем
действительную скорость истечения жидкости из
сопла u0.
Лекция 10
11
24.10.2023
12.
рвВ
р3
III
р1
I
y
lксм
u3
u1
7
6
5
4
z2
3
2
В
x рx
u0
р4
IV
ux
x
I
III
II
II
l1
l2
l3
IV
z1
1
ра
A
Лекция 10
A
12
24.10.2023
13.
Для этого используем уравнение Бернулли длясечений I – I и III – III в виде
p1 u p3 u
u
с
g 2 g g 2 g
2g
2
1
2
0
откуда
u0
p1 p3
2
u1
2 g
g
1 с
2
0
14.
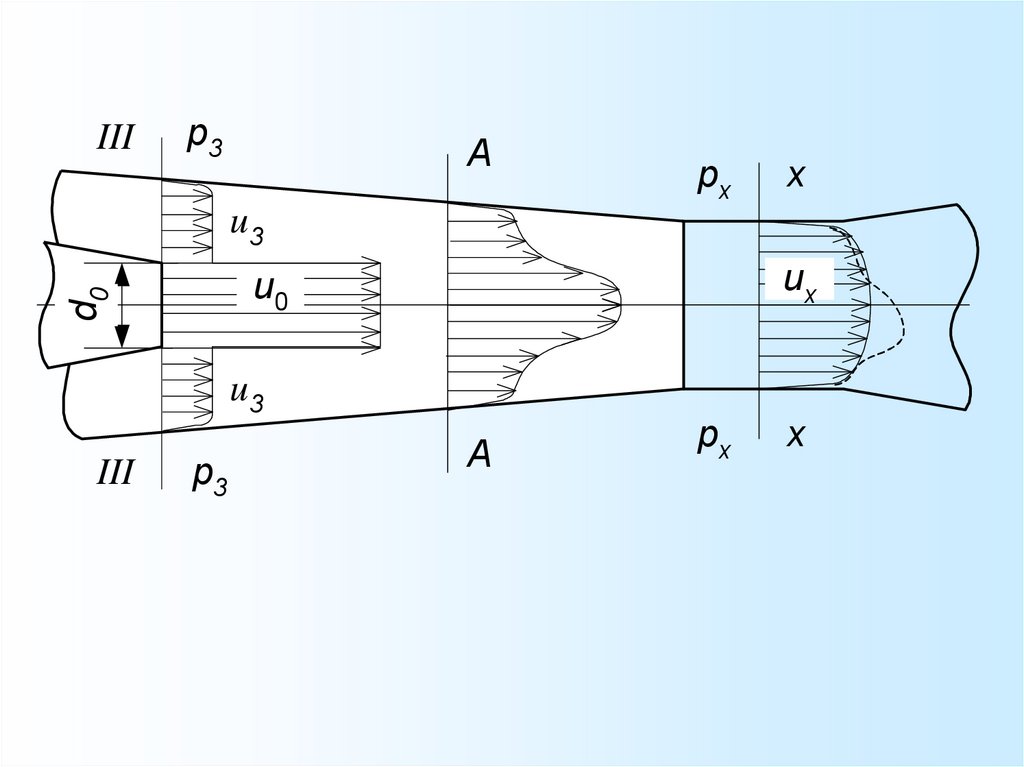
Экспериментальные исследованияпоказывают, что в выходном сечении сопла
скорость u0 практически постоянна; на
расстоянии, равном (4 – 5)∙d0 от сопла,
начинается деформация струи, которая
выражается в уменьшении осевой скорости
струи, а также скоростей частиц,
располагающихся на ее поверхности, что
видно из эпюры скоростей для сечения А–А
камеры смешения.
15.
IIIp3
A
px
x
u3
ux
d0
u0
u3
III
p3
A
px
x
16.
В камере смешения происходит процессвсасывания рабочей струей перекачиваемой
жидкости, сопровождаемый значительными
гидравлическими потерями. Полагают, что
между движущимися потоками жидкости
происходит турбулентный обмен
импульсами, вследствие чего скорость
перекачиваемой жидкости увеличивается, а
струи – уменьшается.
17.
СловарьОдним из наиболее важных параметров
струйного насоса является
коэффициент всасывания, или
коэффициент эжекции, который
представляет собой отношение
секундного количества засасываемой
жидкости G2 к соответствующему
количеству рабочей жидкости G1, т, е.
q G2 G1
Лекция 10
17
24.10.2023
18.
Для составления основного уравненияструйного насоси, определения его КПД и
решения других задач необходимо знать
величину потерь энергии в камере
смешения. Эти потери имеют
гидравлический характер и возникают
вследствие трения жидкости о стенки
камеры смешения и трения в вихревом слое,
отделяющем поверхность струи от потока
перекачиваемой жидкости. Величина
гидравлических потерь в вихревом слое
может составлять до 70% всех
гидравлических потерь струйного насоса.
19.
Гидравлические потери в камере смешенияопределяют как разность полных энергий в
начальном и конечном сечениях камеры
смешения. Для расчетного режима работы,
когда р3 = рх, получим
p3 u 02
p3 u 32
p x u x2
G1
G2
G1 G2 E
g 2 g
g 2 g
g 2 g
20.
Как было уже отмечено, при р3 = рх вводоструйных насосах достигаются
минимальные потери энергии, что возможно
при длине камеры смешения
l1 2,5... 3,5 d x
и длине горловины
l 2 4... 8 d x
где dx – диаметр горловины.
21.
Таким образом, при соблюдениирекомендованных линейных размеров l1 и l2,
которые обычно уточняются путем
испытаний на стенде, последнее уравнение
можно записать следующим образом
u
u
u
G1 G2 E
G1
G2
2g
2g
2g
2
0
2
3
2
x
Это уравнение соответствует минимальным
потерям энергии, уменьшение которых
невозможно для данного типа насоса.
22.
При отсутствии соосности сопла и камерысмешения, при слишком длинной или
слишком короткой камере смешения, или
неудачно выбранном соотношении
диаметров сопла и горловины, эти потери
могут значительно возрасти.
23.
В диффузоре струйного насоса происходитпреобразование кинетической энергии
u
2
x
2g
G1 G2
в потенциальную –
p4
G1 G2
g
до пределов, обусловливаемых допустимой
величиной скорости u4 в нагнетательном
патрубке насоса (сечение IV–IV).
24.
В диффузоре также происходятгидравлические потери энергии, которые
увеличиваются, при прочих равных
условиях, с увеличением неравномерности
распределения скоростей по поперечному
сечению потока.
25.
Если бы в сечении x–x сразу же начиналсядиффузор, то в нем возникли бы большие
гидравлические потери. Для уменьшения
потерь в диффузоре надо дать возможность
потоку произвести выравнивание скорости,
что достигается увеличением длины
горловины l2. При этом, чем больше
предполагается коэффициент всасывания,
тем большей длины должна быть горловина.
Таким образом, наличие горловины
способствует более полному использованию
всасывающей поверхности струи и
улучшает распределение скоростей в потоке
перед вступлением его в диффузор.
26.
Коэффициент потерь энергии в диффузоре взависимости от степени равномерности
распределения скоростей перед входом в
него находится в пределах
д 0,1... 0,3
27.
Применяя к сечениям х–х и IV–IV законсохранения энергии, получим
p x u x2
G1 G 2
g 2 g
2
p 4 u 42
u x
G1 G 2 д
G
G
1
2
g
2
g
2g
28.
Из рассмотрения этого уравнения и рисункаследует, что при больших величинах рв, z2
или значительных потерях напора в
нагнетательном трубопроводе Sh2
необходимо иметь большую величину
давления р4, что возможно только за счет
большой скорости в горловине uх.
29.
Увеличение же этой скорости можетвызвать увеличение коэффициента
кинетической энергии и коэффициента
неравномерности распределения скоростей
по поперечному сечению b, т. е.
существенное увеличение потерь энергии в
диффузоре. Поэтому водоструйные насосы
нецелесообразно применять в качестве
высоконапорных насосов.
30.
Во всасывающей полости или головке 4водоструйного насоса происходят
гидравлические потери, величина которых
не больше, чем в соответствующих
криволинейных каналах. Однако при
чрезмерной высоте всасывания насоса в его
головке может возникнуть явление
кавитации.
31.
Кавитация может возникнуть и в горловине6, если давление в ней рх будет равно
упругости паров жидкости рs при данной ее
температуре. Для устранения этого явления
необходимо, чтобы давление в начале
камеры смешения р3 было больше упругости
паров перекачиваемой жидкости примерно
на (10…15) кПа.
32.
Пользуясь рисунком для всасывающейстороны водоструйного насоса, можно
написать закон сохранения энергии сначала
для уровня А–А и сечения II–II, а затем для
сечений II–II и III-III в таком виде
2
2
pа
p2 u
z1 h1 ;
g g 2 g
2
2
2
3
2
3
p3 u
u
p2 u
y гол
.
g 2 g g 2 g
2g
33.
Преобразовав эти уравнения, получим2
2
а
3
3
3
гол
1
p
p
u
y
g g 2 g
где
u
z h1
2g
2
3
u
y гол
h
2g
можно рассматривать как динамическое
падение давления в полости всасывания.
34.
Допустимое разряжение на входе вводоструйный насос
H
доп
вак
pа p s u
h
g
2g
2
3
35.
Так как2
3
u
y
2g
то окончательно получим
H
доп
вак
pа p s
u
гол
g
2g
2
3
36.
Основное энергетическое уравнение,параметры и характеристики жидкостных
струйных насосов
Для проектирования и эксплуатации
струйного насоса необходимо знать
зависимость между его рабочими
параметрами и степень полезного
использования энергии рабочей жидкости.
Как эти, так и некоторые другие задачи
решаются при помощи основного
энергетического уравнения, которое
получают из уравнений энергий для головки,
сопла, камеры смешения и диффузора
водоструйного насоса.
Лекция 10
36
24.10.2023
37.
Если в этих уравнениях полный запас удельнойэнергии жидкости обозначить как:
2
1
p1 u
H1
g 2 g
– для рабочей жидкости
во входном сечении сопла;
2
2
p2 u
H2
g 2 g
– для перекачиваемой
жидкости во всасывающем
патрубке струйного насоса;
2
4
p4 u
H4
g 2 g
– для выходного сечения
диффузора
или нагнетательного патрубка струйного насоса,
38.
то основное энергетическое уравнение будетиметь такой вид:
H 1G1 H 4 G 2 H 2 G 2 yG 2
2
0
u
H 4 G1 E с
G1
2g
u
u
G1 G 2
гол
G2 д
2g
2g
2
3
2
x
39.
Левая часть этого уравнения представляетсобой мощность, затрачиваемую на
действие струйного насоса.
Сумма первых трех членов правой части
уравнения является полезной мощностью
струйного насоса, работающего в качестве
эжектора
N э H 4 H 2 y G2 H э G2
При этом, четвертый и последующие
слагаемые этой же части уравнения
являются потерями энергии.
40.
Если струйный насос используется вкачестве инжектора, то полезной является
мощность
N и H 4 H 2 y G2 H 4 G1
41.
Общая оценка потерь энергии может бытьдана полным КПД насоса, который является
отношением его полезной мощности к
мощности, потребляемой насосом. Из
рассмотренного характера потерь энергии
следует, что КПД струйного насоса является
гидравлическим КПД.
42.
Величина его может быть определена поуравнениям:
- для эжектора
N э G2 H э
Hэ
э
q
N 1 G1 H 1
H1
- для инжектора
Hэ H4
Nи
и
q
N1
H1 H1
43.
Из ранее установленного понятия эжектораи инжектора следует и различная
количественная оценка их эффективности.
Из всех параметров струйного насоса
наиболее важными являются коэффициент
всасывания q и напор Hэ, взаимная связь
которых с другими величинами может быть
получена при помощи уравнения энергии
насоса.
44.
Разделив это уравнение на G1, получимH 1 qH э H 4 e
2
0
2
3
2
x
u
u
u
с
q гол
1 q д
2g
2g
2g
где
e E G1
45.
Таким образом, при заданном напорерабочей жидкости Н1 и определенных
потерях энергии, что оценивается суммой
последних членов уравнения, изменение
коэффициента всасывания q возможно
только за счет напора Hэ. Из этого же
уравнения следует, что, например,
высоконапорные струйные насосы не могут
иметь большого коэффициента всасывания.
46.
Для заданных параметров Н1 и Hэдействительная величина коэффициента
всасывания может быть определена только
при помощи КПД струйного насоса.
Величину коэффициента всасывания можно
вычислить при помощи уравнения
G2 u0 bu x
q
G1 bu x u3
47.
которое, после подстановки соответствующихвыражений для скоростей, преобразуется к
виду
1
q
1 с
b
p1 p3
px
b
2
u1
2 g
2 g H 4
g
1 д
g g
1 д
px
1
2 g H 4
g
гол
p а ps
доп
2 g
H вак
g
48.
Следовательно, коэффициент всасываниязависит от многих величин ( , b, zc, zд и
zгол), которые в свою очередь зависят от
конструктивных особенностей насоса и его
режима работы, т. е. от числа Рейнольдса.
Из этого уравнения видно, что при заданном
давлении р1 рабочей жидкости коэффициент
q уменьшается при совместном или
раздельном увеличении высоты нагнетания
H4 и высоты всасывания. Увеличение q с
уменьшением вакуумметрической высоты
всасывания объясняется возможностью
увеличения при этом u3.
49.
Теоретическая напорно-расходная характеристикаэжектора, получаемая при условии, что в насосе
потери энергии отсутствуют, имеет вид
гиперболы
H3
H 1G1 const
H т.э
G т2
G т2
a
При H1>H1'>H1"
0
b
G2
50.
Наличие гидравлических потерь длявысоконапорных насосов существенно
изменяет количественные соотношения
между этими параметрами, что
иллюстрируется группами графиков а и b.
Показанное здесь значительное отличие
основных характеристик водоструйных
насосов объясняется существенным
взаимным влиянием геометрических
размеров на потери энергии и коэффициент
всасывания.
51.
ВыводыЛекция 10
51
24.10.2023
52.
Источники дополнительныхсведений
Лекция 10
52
24.10.2023



















































 mechanics
mechanics industry
industry








