Автомат с магазинной памятью

1.

АВТОМАТ С
МАГАЗИННОЙ
ПАМЯТЬЮ

2.

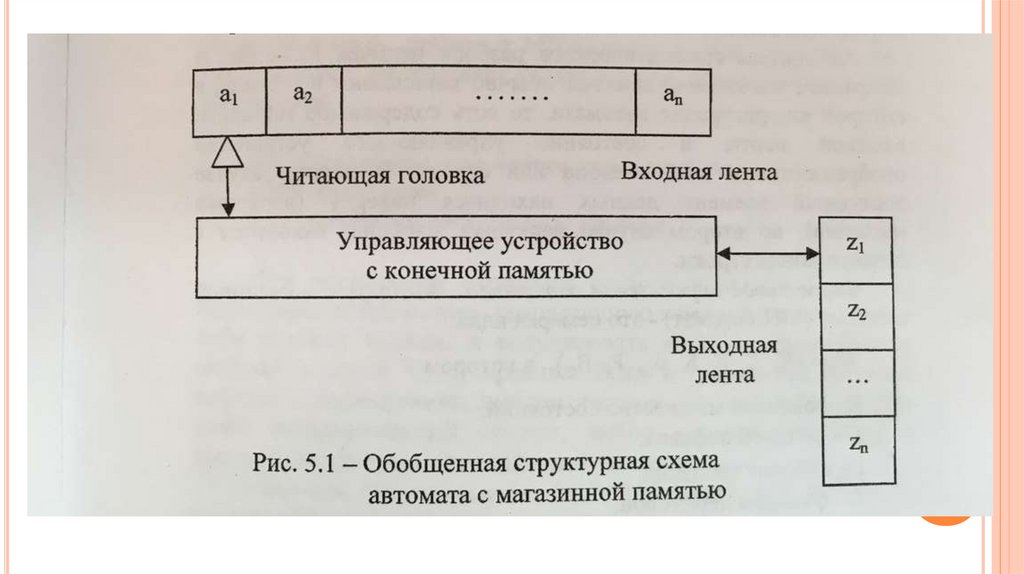
Неформальное определение автомата.
Автоматы с магазинной памятью (МПавтоматы) соответствуют контекстносвободным грамматикам и являются
распознавателями контекстно-свободных
языков. МП-автомат имеет входную ленту,
управляющее устройство с конечной
памятью для хранения номера текущего
состояния, дополнительную память (или
рабочую ленту) неограниченного объема,
обобщенная структура которого приведена
на рисунке

3.

4.

Рабочая лента представляет собой
вспомогательное устройство для хранения
информации и работает по принципу LIFO
(Last Input First Output), то есть в каждый
момент времени доступен только тот
элемент, который был добавлен в магазин
позже остальных элементов. Этот элемент
находится в верхушке магазина, а его адрес
хранится в указателе стека. Данные с
рабочей ленты могут считываться автоматом
и могут записываться на нее.

5.

Входная лента - это также линейная
последовательность ячеек, каждая из которых
содержит один символ из входного алфавита.
Управляющее устройство может быть:
а) недетерменированным. если на следующем
такте для автомата существует некоторое
множество команд, одну из которых автомат
может выполнить;
б) детерминированным. если на следующем
такте определена единственная команда.

6.

Алгоритмы грамматического разбора
цепочек КС-языков и автоматов с
магазинной памятью обычно записывают в
таблице, некоторой конфигурации
автомата, то есть содержимое магазина,
входной ленты и состояние управляющего
устройства отображаются в виде столбца
или строки. В первом случае доступный
элемент данных находится наверху
(верхушке магазина). во втором случае
верхушка магазина находится с правого
конца строки.

7.

Формальное определение автомата. Автомат с
магазинной памятью (МП-автомат) - это семерка
вида:
М = (К, Σ, Г, δ, р0, F, В0), в котором
К - конечное множество состояний,
Σ — входной алфавит.
Г- алфавит магазина
δ - функция переходов, р0 - начальное состояние,
F - множество заключительных состояний,
В0 — символ для обозначения маркера дна
магазина.

8.

Язык, распознаваемый МП-автоматом
L(М), представляет собой множество всех
слов, допускаемых (читаемых,
распознаваемых) этим автоматом.
За один такт работы МП-автомат
выполняет одну команду функции
переходов. Для описания действий,
выполненных автоматом, пользуются
понятием конфигурации, которая
представляет произвольную тройку:

9.

АЛГОРИТМЫ ГРАММАТИЧЕСКОГО РАЗБОРА
В МП-АВТОМАТЕ. АЛГОРИТМ ВОСХОДЯЩЕГО РАЗБОРА
При восходящей стратегии разбора в заданной
цепочке необходимо найти основу,
совпадающую с правой частью какого- либо
правила вывода, и редуцировать ее к
нетерминальному символу в левой части
правила. Если в грамматике имеются правила с
одинаковыми левыми частями, то необходимо
найти такой нетерминальный символ, выбор
которого приводит к распознаванию автоматом
заданной цепочки.

10.

Алгоритм функционирования МП-автомата, выполняющего
восходящий разбор, включает следующие этапы:
1.
Любой символ, прочитанный с входной ленты, записывается
в магазин.
2.
Если в верхушке магазина сформирована основа,
совпадающая с зеркальным отображением правой части
какого- либо правила вывода, то она заменяется на
нетерминальный символ в левой части этого правила.
3.
Действия п.п.1 и 2 в некоторой последовательности
повторяются до тех пор, пока не будет полностью прочитана
входная цепочка.
4. Если после п.З в магазине получена аксиома выполняется
команда завершения разбора.

11.

В соответствии с этим алгоритмом для КС-грамматики
G=(Vt, Vn, P, S), можно построить эквивалентный МПавтомат М = (К, Σ, Г, δ, р0, F, В0), в котором:
К = {р0, f} — конечное множество состояний управляющего
устройства;
Σ = VT — алфавит;
Г = VT U VN U {В0} — алфавит магазинной памяти;
р0 — начальное состояние;
F — множество заключительных состояний, причем F= {f};
В0 ϵ Г - маркер дна магазинной памяти;
δ - функция переходов, которая включает команды трех
видов:

12.

а) команды записи терминальных символов, прочитанных
с входной ленты, в магазин:
Р0, а, ε —> Ро, а, где в правой части команды р0 ϵ К начальное состояние управляющего устройства;
а ϵ VT - символ, считанный автоматом с входной ленты;
ε ϵ Г - символ в верхушке магазинной памяти; в левой
части команды р0 ϵ К- состояние управляющего
устройства, т.е. после выполнения данной команды
состояние управляющего устройства МП-автомата не
изменяется;
а ϵ Г — символ, считанный с входной ленты, записан в
верхушку магазинной памяти;

13.

б) команды редукции по правилам
грамматики:
р0, ε,ф —>Р0, А,
где в правой части команды р0 ϵ К начальное состояние управляющего
устройства;
ф - сформированное в верхушке магазинной
памяти зеркальное отображение правой
части правила грамматики А -> ф;
в левой части команды р0 ϵ К — начальное
состояние управляющего устройства;

14.

) команда завершения разбора:
P0,ε,SB0— f,B0,
где в правой части команды р0 ϵ К - начальное
состояние управляющего устройства;
ε ϵ Σ*- пустой символ на входной ленте (входное
слово прочитано);
SB0 — символы в магазинной памяти: S - аксиома,
В0- маркер дна магазинной памяти;
в левой части команды f ϵ F - заключительное
состояние управляющего устройства;
В0 - маркер дна магазинной памяти.
в

15.

АЛГОРИТМ НИСХОДЯЩЕГО РАЗБОРА
На каждом шаге нисходящего разбора применяется
некоторое правило из множества Р. Алгоритм
функционирования эквивалентного МП-автомата,
выполняющего нисходящий разбор, включает
следующие этапы:
В начальный момент времени в магазинную
память записывается аксиома.
Каждый нетерминальный символ А в верхушке
магазинной памяти заменяется на правую часть
правила грамматики в соответствии с правилом
А —> ф ϵ Р.

16.

Если в верхушке магазинной памяти получен
терминальный символ, то он сравнивается с
символом, считанным с входной ленты. Если эти
символы совпадают, то символ в верхушке
магазинной памяти стирается.
Действия п.п. 2 и 3 повторяются до тех пор, пока
не будет прочитана вся входная цепочка.
Если после п.4 в магазине находится только
символ маркера дна магазина, то выполняется
команда окончания разбора.

17.

В соответствии с этим алгоритмом для КС-грамматики
G=(Vt, Vn, P, S) можно построить эквивалентный МПавтомат М = (К, Σ, Г, δ, р0, F, В0), в котором:
К = {р0, р1, f} — конечное множество состояний
управляющего устройства;
Σ = VT —алфавит;
Г = VT U VN U {В0} —алфавит магазинной памяти;
р0- начальное состояние;
F = {f} — множество заключительных состояний;
В0 ϵ Г - маркер дна магазинной памяти;
δ - функция переходов, которая включает команды
четырех видов;

18.

а) команда записи аксиомы в магазинную память:
р0,ε, ε —> p1 S, где в правой части команды р0 ϵ К - начальное
состояние управляющего устройства;
ε ϵ Σ - символ на входной ленте; ε ϵ Г - символ в верхушке
магазинной памяти; в левой части команды р1 ϵ К. - новое
состояние управляющего устройства;
S ϵ VN - аксиома, записанную в верхушку магазина;
б) команда замены нетерминального символа в верхушке
магазинной памяти на правую часть правила вывода:
р1, ε,А —> р1,ф, где в правой части p1 ϵ К — состояние
управляющего устройства;
ε ϵ Σ — символ на входной ленте;
А ϵ VN - нетерминальный символ в верхушке магазинной памяти;
в левой части р1 ϵ К - состояние управляющего устройства; фправая часть правила А—> ф ϵ Р;

19.

в) команда сравнения терминального символа, считанного с входной
ленты, с терминальным символом, полученным в верхушке магазинной
памяти:
р1, а, а —>р1,ε, где в правой части р1 ϵ К - состояние управляющего
устройства;
a ϵ VT - символ, читаемый с входной ленты;
a ϵ Г - символ в верхушке магазинной памяти; в левой части р1 ϵ К состояние управляющего устройства; ε ϵ Г — символ в верхушке
магазинной памяти;
г) команда завершения разбора:
р1, ε, В0 -> f, В0
где в правой части р1 ϵ К - состояние управляющего устройства,
ε ϵ Г — символ в верхушке магазинной памяти;
В0 ϵ Г — маркер дна магазинной памяти;
в левой части f ϵ К - заключительное состояние управляющего устройства;
B0 - маркер дна магазинной памяти.