Similar presentations:
Функции, непрерывные на отрезке. Тема 8
1.
2.
§8. Функции, непрерывные наотрезке
Функция y f (x ) называется непрерывной
на отрезке [ a; b ], если она непрерывна в
каждой точке интервала ( a; b ), в точке x a
непрерывна справа, а в точке x bнепрерывна
слева.
3.
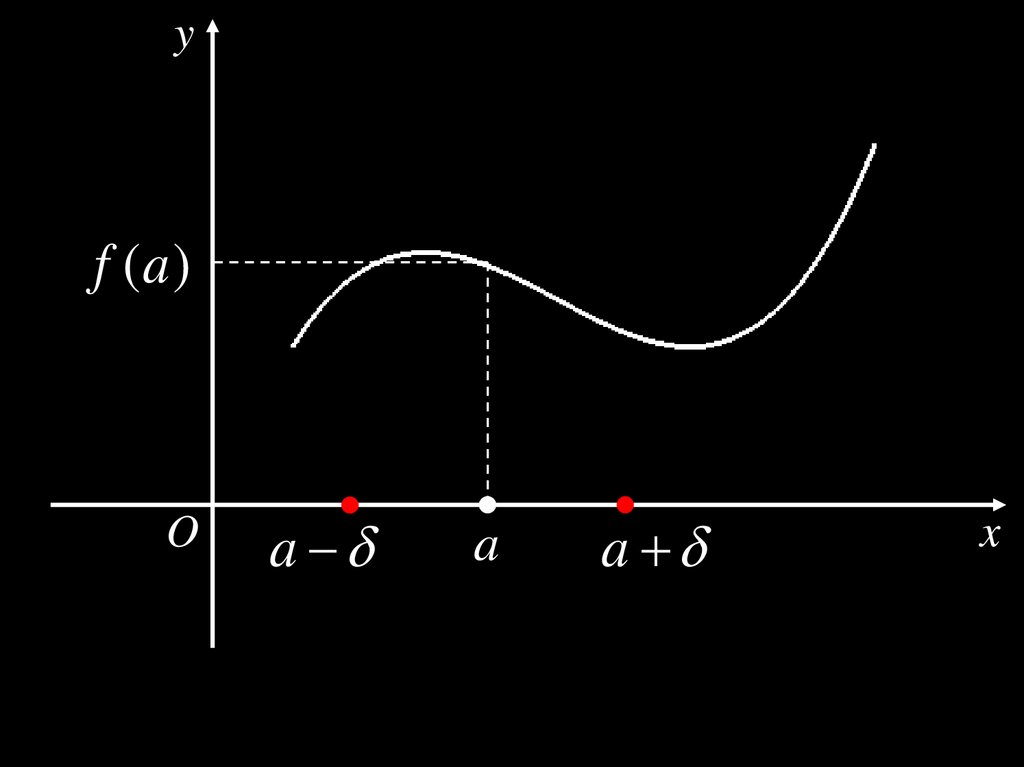
Теорема 1. (Об устойчивости знака)Пусть функция y f (x ) непрерывна в точке a
и f ( a ) 0. Тогда существует -окрестность
точки a такая, что в этой окрестности функция
y f (x ) имеет тот же знак, что и f (a ).
4.
yf (a )
O
a
a
a
x
5.
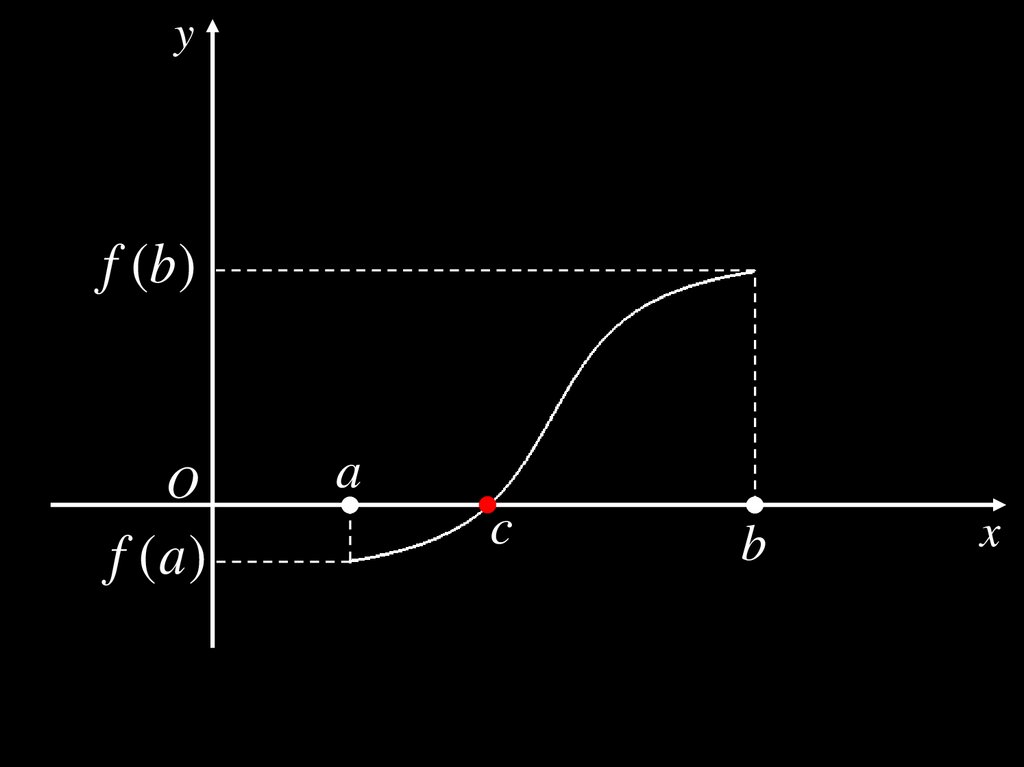
Теорема 2. (Первая теорема Больцано–Коши)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ],
на концах отрезка принимает значения
разных знаков: f ( a ) f (b ) 0.
Тогда
c ( a; b ) :
f (c ) 0.
6.
yf (b )
O
f (a )
a
c
b
x
7.
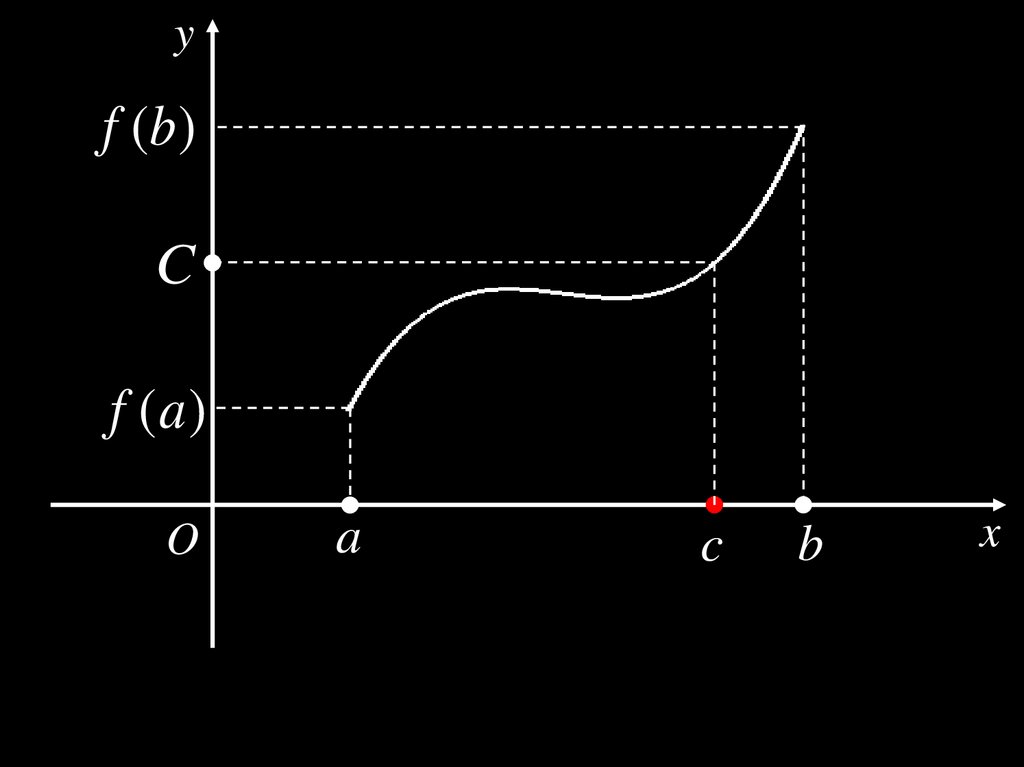
Теорема 3. (Вторая теорема Больцано–Коши)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ],
f ( a ) f (b ),
f ( a ) C f (b ).
Тогда
c ( a; b ) :
f (c ) C .
8.
yf (b )
C
f (a )
O
a
c
b
x
9.
Теорема 4. (Первая теорема Вейерштрасса)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ].
Тогда
она ограничена на этом отрезке.
10.
Теорема 5. (Вторая теорема Вейерштрасса)Пусть
функция y f (x ) непрерывна на отрезке [ a; b ].
Тогда
в некоторых точках этого отрезка она
достигает своего максимума и минимума.
, [ a; b ] :
max f ( x ) f ( )
x [ a ;b ]
min f ( x ) f ( )
x [ a ;b ]







 mathematics
mathematics








