Ғажайып сандар

1. Ғажайып сандар

Орындаған: 5 «А» сынып оқушысы
Мамай Аянат

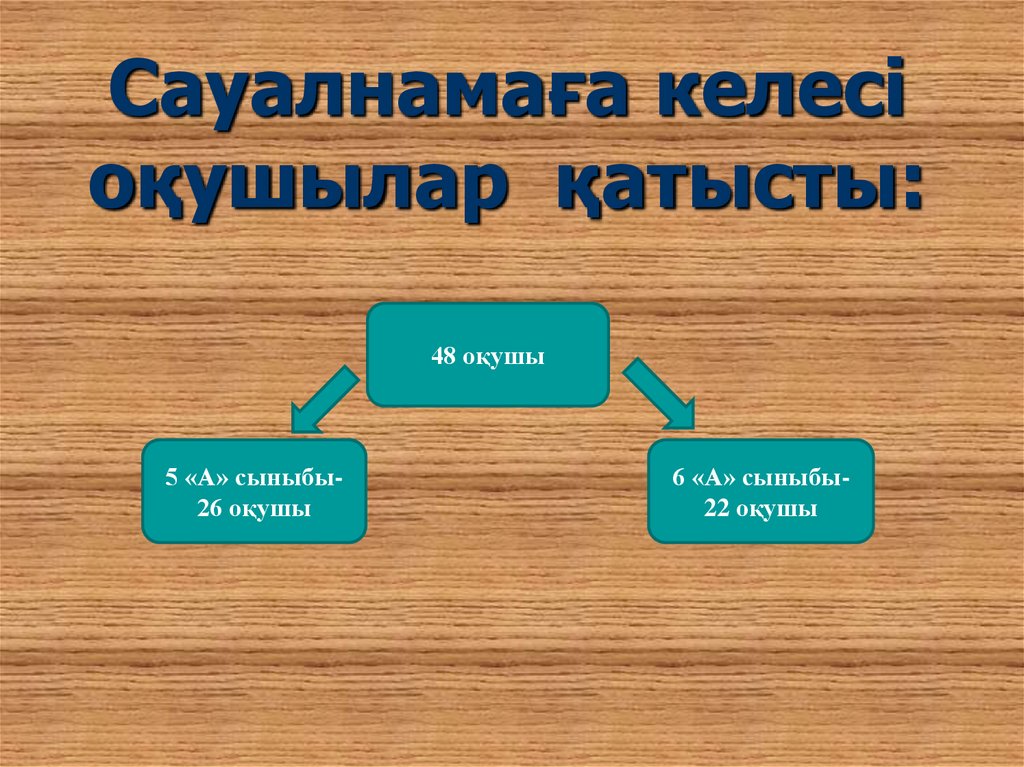
2. Сауалнамаға келесі оқушылар қатысты:

48 оқушы
5 «А» сыныбы26 оқушы
6 «А» сыныбы22 оқушы

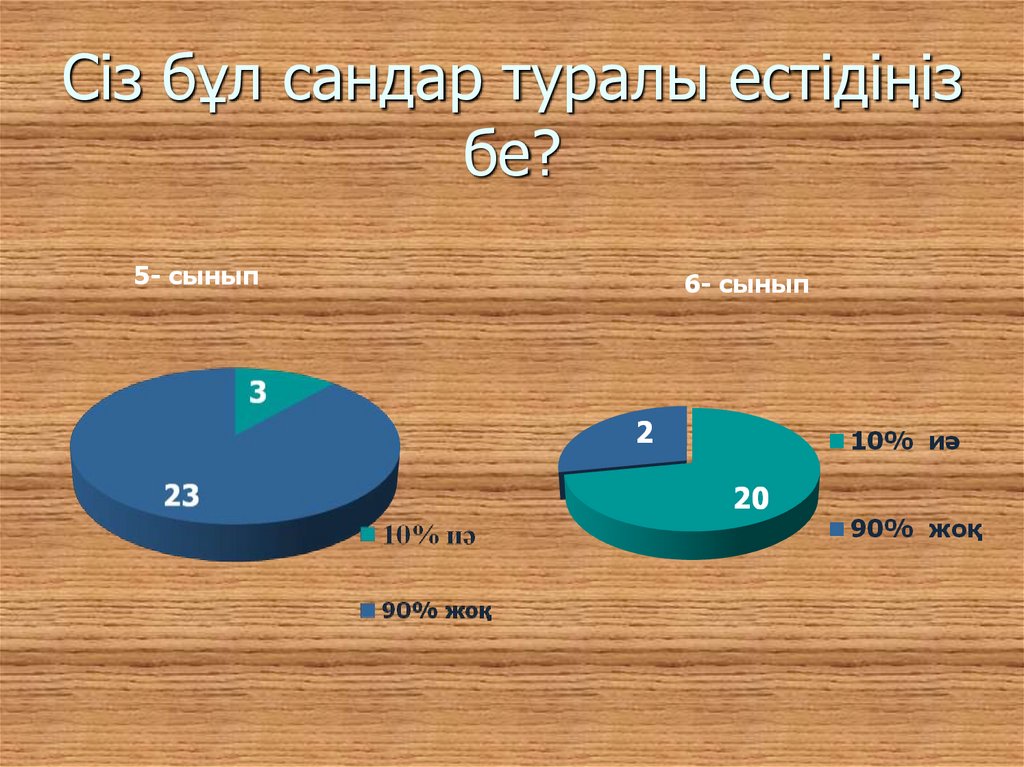
3. Сіз бұл сандар туралы естідіңіз бе?

5- сынып
6- сынып

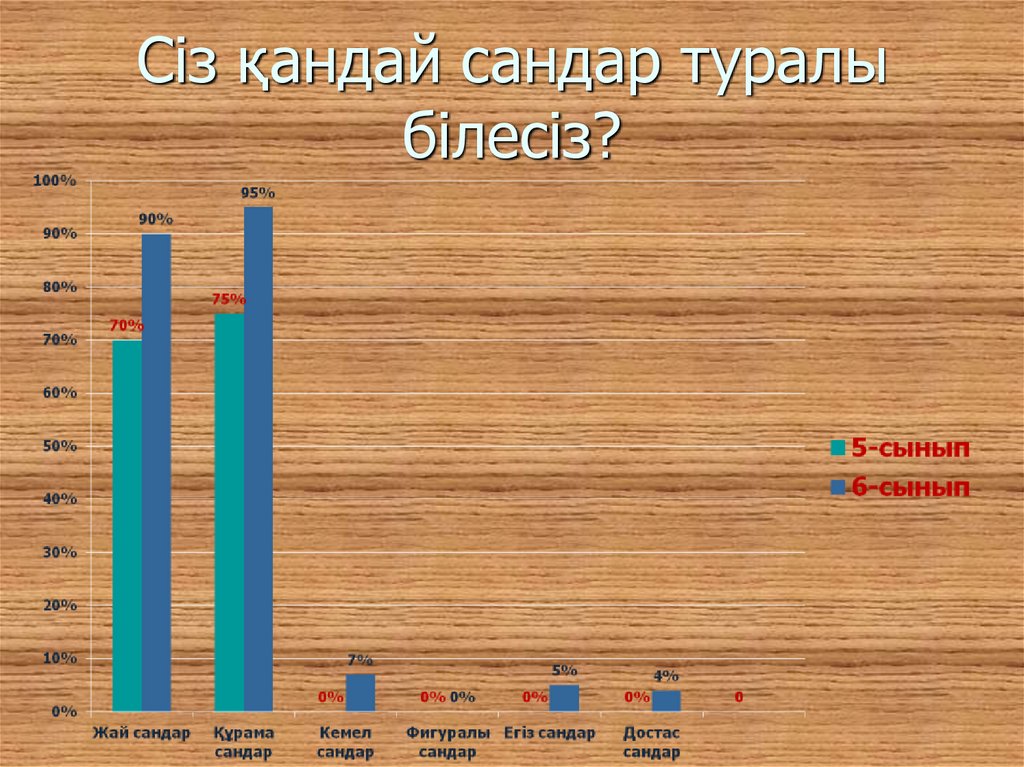
4. Сіз қандай сандар туралы білесіз?

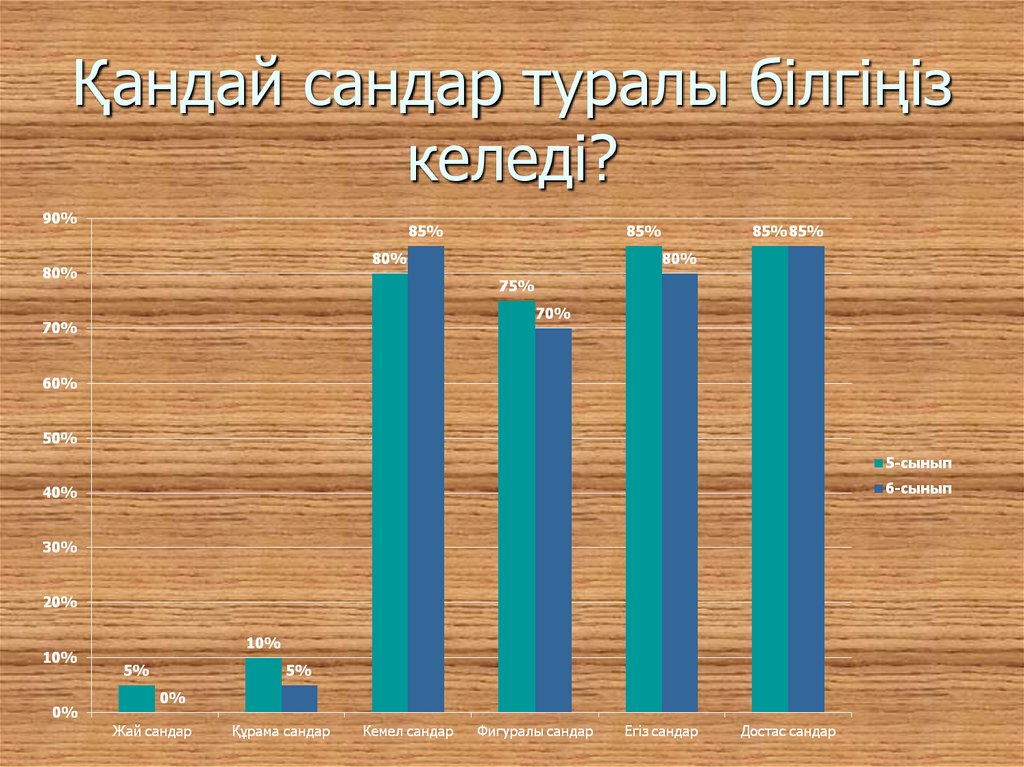
5. Қандай сандар туралы білгіңіз келеді?

6.

Зерттеу жұмысының мақсаты:
таңғажайып сандармен танысу және жай сандардың
қасиеттері арқылы олардың рөлін арттыру.
Зерттеу міндеттері:
а) тақырып бойынша кітаптарды қарау және
меңгеру.
ә) мектеп бағдарламасында кездеспейтін натурал
сандардың тарихи деректерін талдау.
б) ғажайып сандарды табудың әдіс-тәсілдері
арқылы оқушыларды математикаға
тартып,қызықтыру.
в)Фигуралы, палиндром және репьюнит сандармен
танысу.

7.

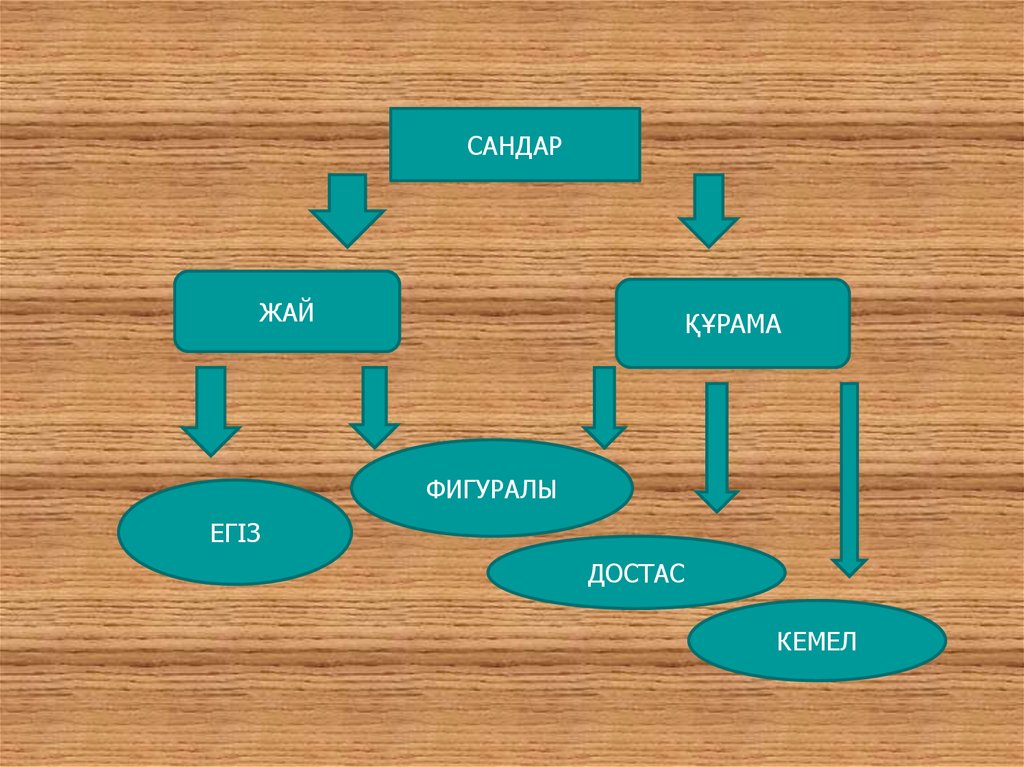
Жоспар
1. Кіріспе
2. Жай сандар
3. Егіз сандар
4. Кемел сандар
5. Достас сандар
6. Фигуралы сандар
7. Палиндромдар мен репьюниттер
8. Қорытынды

8.

САНДАР
ЖАЙ
ҚҰРАМА
ФИГУРАЛЫ
ЕГІЗ
ДОСТАС
КЕМЕЛ

9. Жай сандар

Екі ғана бөлгіші бар сандар жай сандар
деп аталады.
5=1·5
29=1·29
2
Ең кіші жұп жай сан.

10.

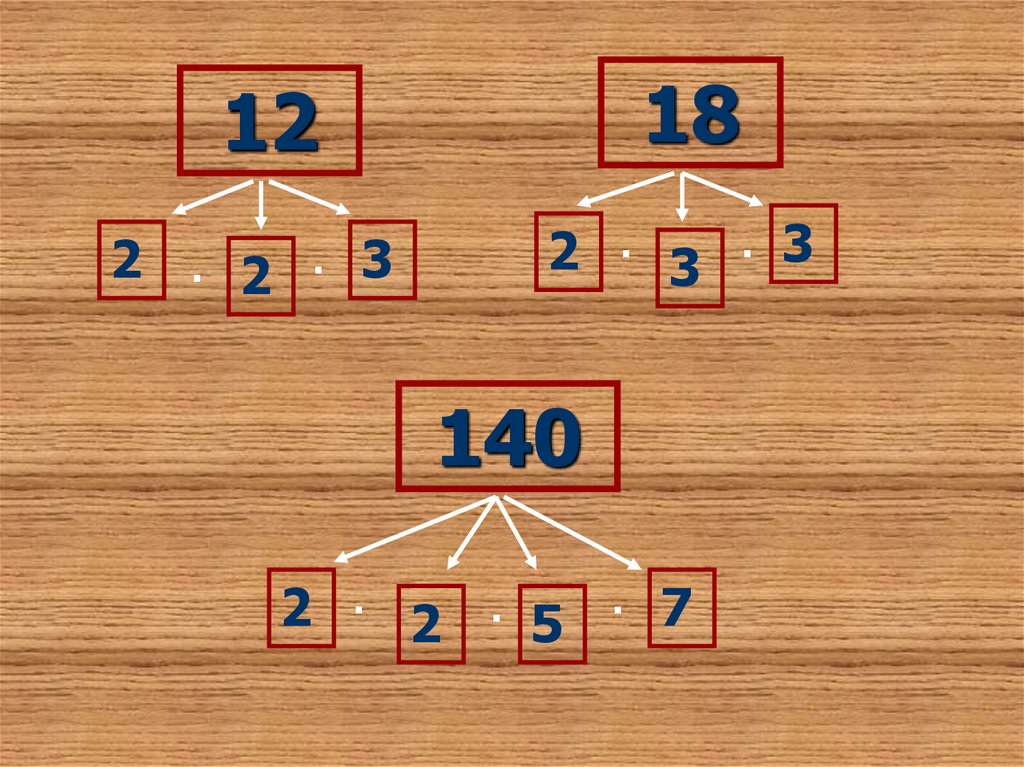
18
12
2
·
2
·
2
3
·
3
·
7
140
2
·
2
·
5
·
3

11.

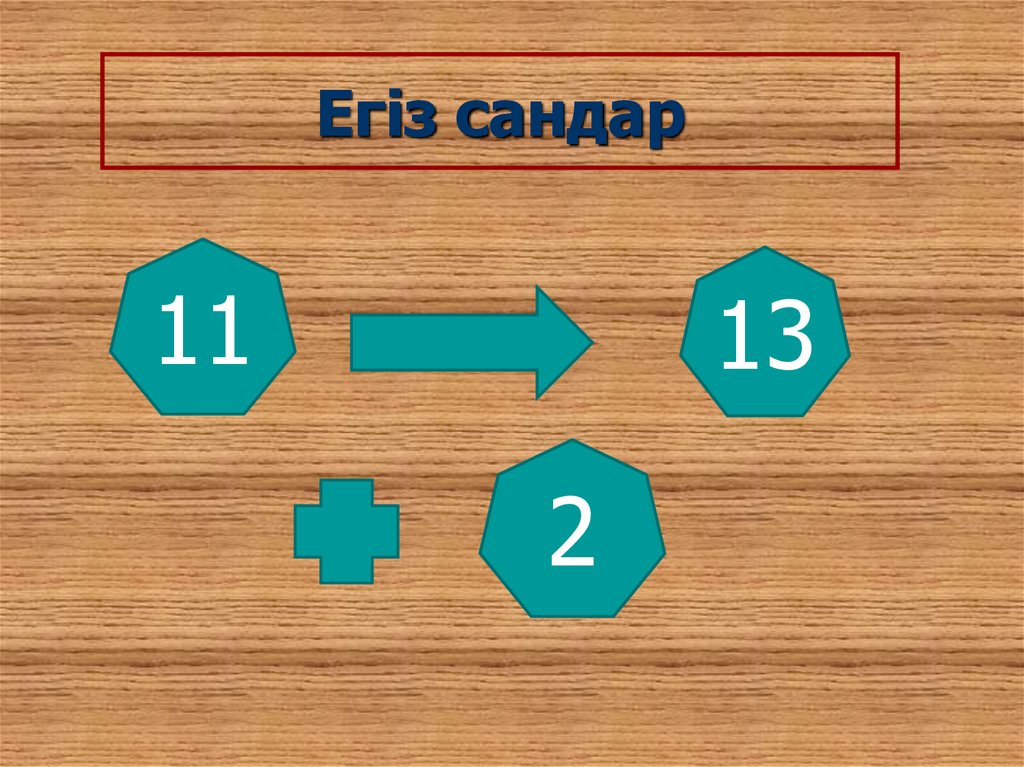
Егіз сандар
11
13
2

12.

№1
№2
№3
№4
№5
№6
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

13.

№1
2
8
14
20
26
32
38
50
56
62
68
74
80
86
№2
3
9
15
21
27
33
39
51
57
63
69
75
81
87
№3
4
10
16
22
28
34
40
52
58
64
70
76
82
88
№4
5
11
17
23
29
35
41
53
59
65
71
77
83
89
№5
6
12
18
24
30
36
42
54
60
66
72
78
84
90
№6
7
13
19
25
31
37
43
55
61
67
73
79
85
91
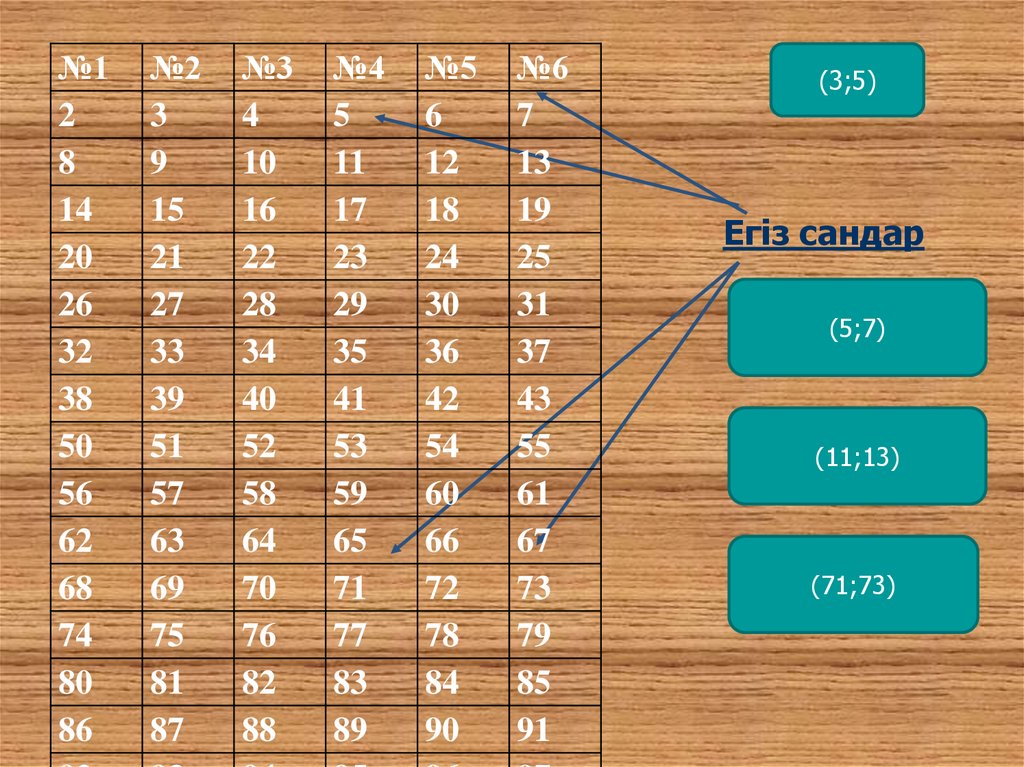
(3;5)
Егіз сандар
(5;7)
(11;13)
(71;73)

14. Кемел сандар

Егер п натурал санының өзінен басқа бөлгіштерінің
қосындысы, n натурал санның өзіне тең болса,
онда n саны кемел сан деп аталады
6
1
3
2
+
+
6
28
1
+2
4
+
28
7
+
14
+

15. Кемел сандар

6,
28,
496,
8128,
33550336,…

16. Пифагор

Достас сандар
Пифагор
1
220 және 284
284 71
2
2
1+2+4+71+142=220
220
1
2
11
2 5
1+2+4+5+10+11+20+22+44+55+110=284

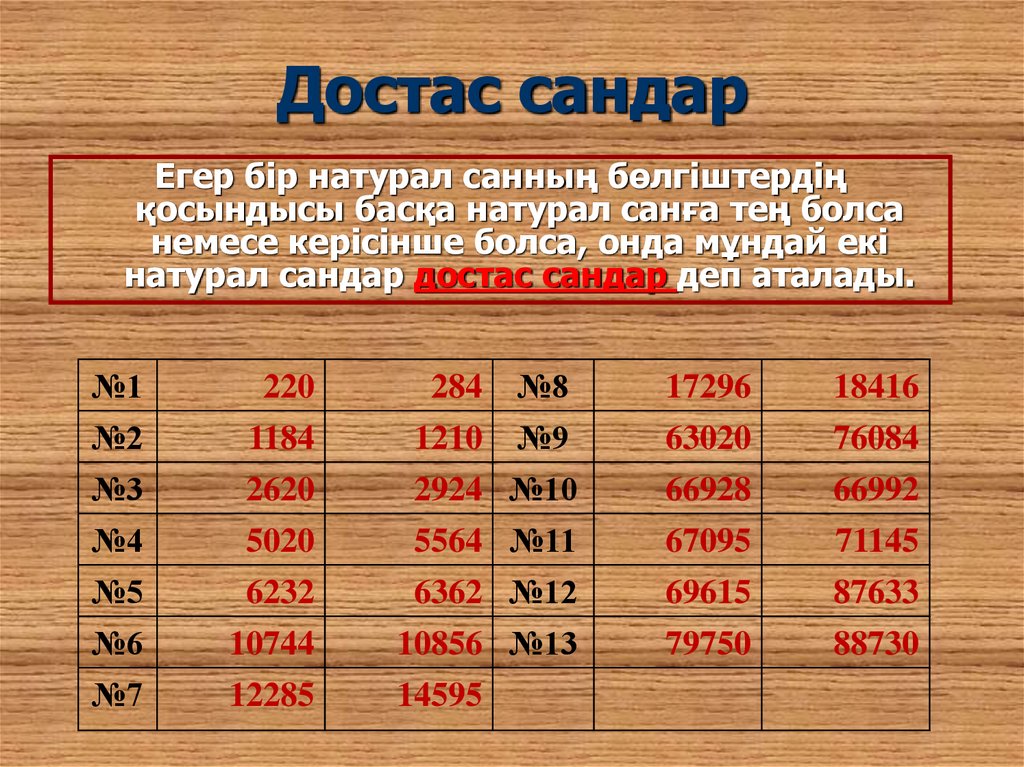
17. Достас сандар

Егер бір натурал санның бөлгіштердің
қосындысы басқа натурал санға тең болса
немесе керісінше болса, онда мұндай екі
натурал сандар достас сандар деп аталады.
№1
№2
№3
№4
№5
№6
№7
220
1184
2620
5020
6232
10744
12285
284
1210
2924
5564
6362
10856
14595
№8
№9
№10
№11
№12
№13
17296
63020
66928
67095
69615
79750
18416
76084
66992
71145
87633
88730

18. Фигуралы сандар

Бұл геометриялық фигуралар арқылы
бейнелеуге болатын сандар.
- 1 саны

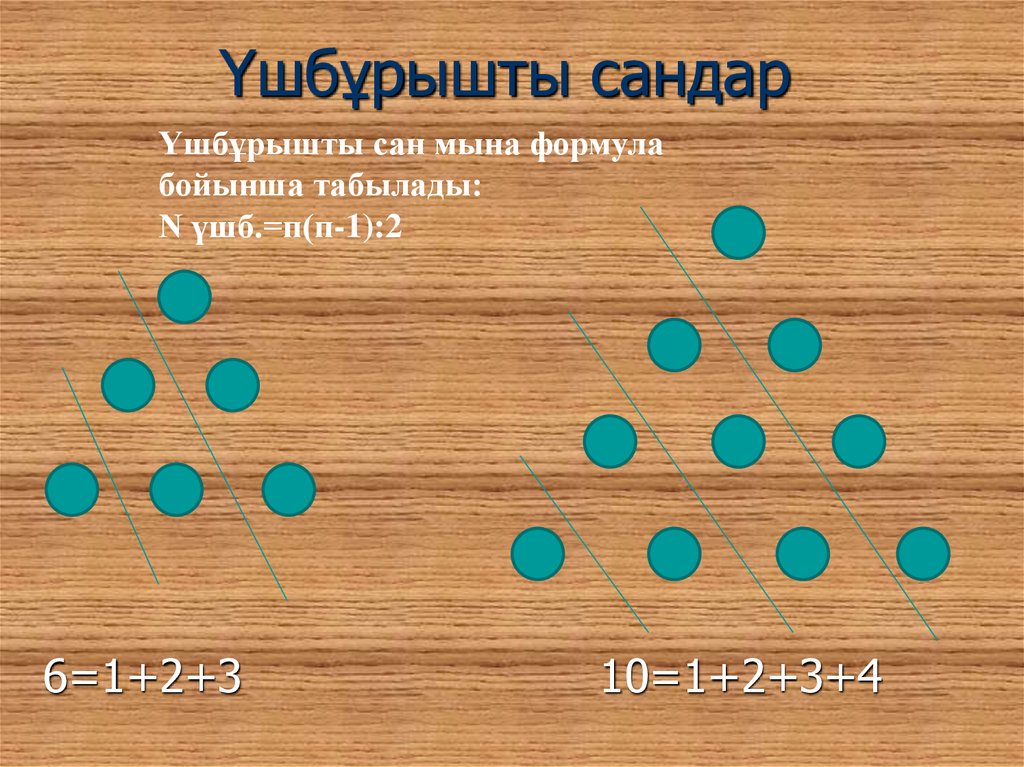
19. Үшбұрышты сандар

Үшбұрышты сан мына формула
бойынша табылады:
N үшб.=п(п-1):2
6=1+2+3
10=1+2+3+4

20. Квадрат сандар

4=2*2
9=3*3
16=4*4
Квадрат сандар формуласы:
N шаршы = п * п

21.

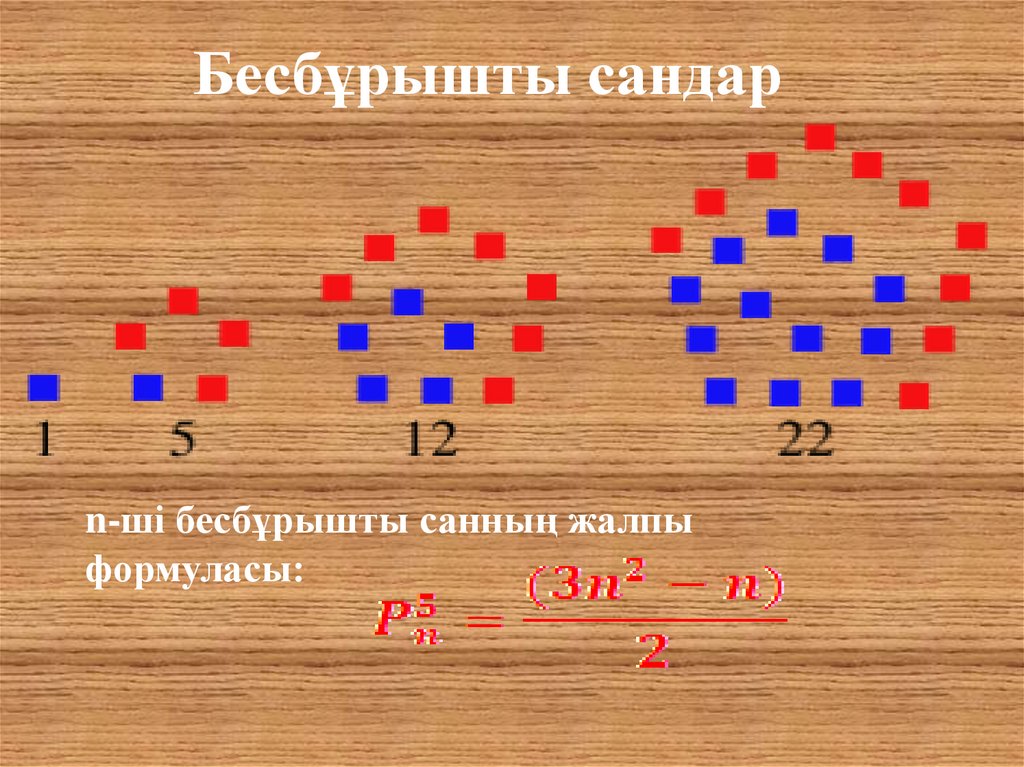
Бесбұрышты сандар
n-ші бесбұрышты санның жалпы
формуласы:

22. Палиндромдар мен репьюниттер

Палиндром-гректің "palindromos" сөзі - "артқа жүгіру
немесе кері жүруші"
565, 505, 23732
Фигуралы сандар-676, 1001 (шаршы және бесбұрыш);
Смит сандары - 45454, 983389.
2222222- атап айтқанда репдиджит сан.
96+69=165,
165+561=726,
726+627=1353,
1353+3531=4884.

23.

Репьюниттер-бұл тек бірліктерден тұратын сандар,
яғни 1-ден тұратын сандар.
Мысалы::
11×11=121;
11∙111=1221;
1111∙11=12221;
111*111=12321;

24. ҚОРЫТЫНДЫ

Натурал сандарды жай көбейткіштерге
жіктеу арқылы табылған сандарды
"кірпіштер" деп айтатын болсақ, онда
оларды "қалау" арқылы керемет "сандар
қамалын“ алуға болатынын көрдік.

25.

Назарларыңызға рахмет