Similar presentations:
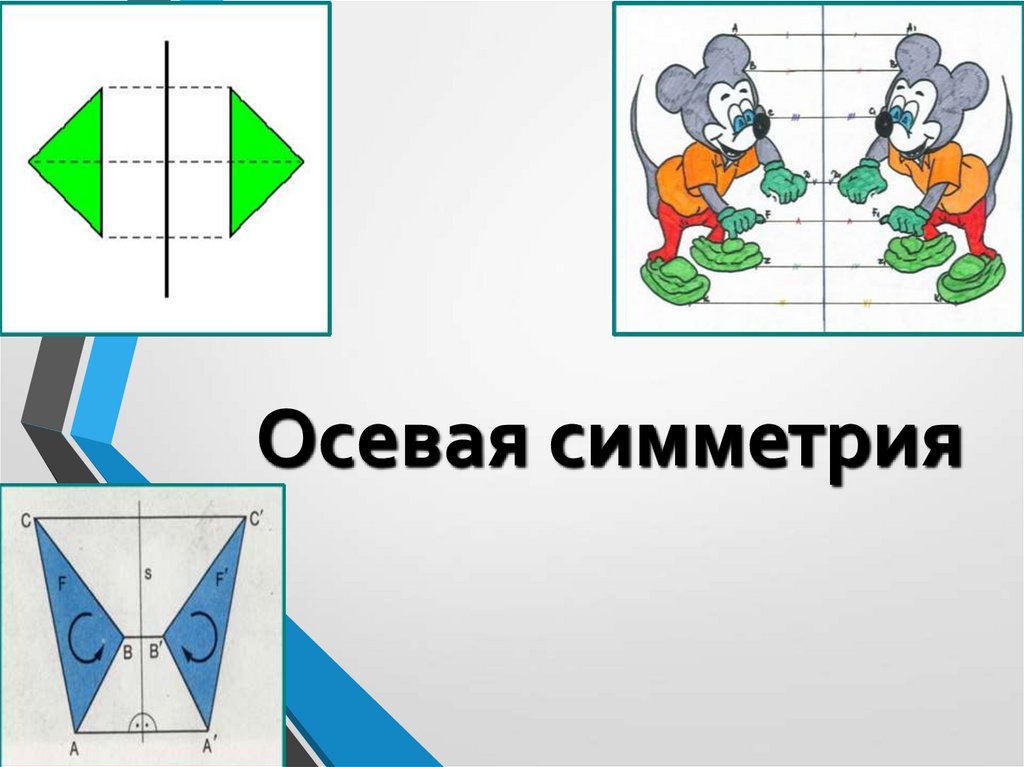
Осевая симметрия
1. Осевая симметрия
2. Осевая симметрия
Две точки А и А1 называются симметричными относительнопрямой а, если эта прямая проходит через середину отрезка
АА1 и перпендикулярна к нему. Каждая точка прямой а
считается симметричной самой себе.
3.
Фигура называетсясимметричной
относительно прямой a,
если для каждой точки
фигуры симметричная ей
точка относительно прямой
а также принадлежит этой
фигуре.
Прямая а называется
осью симметрии фигуры.
Говорят также, что
фигура обладает осевой
симметрией.
а
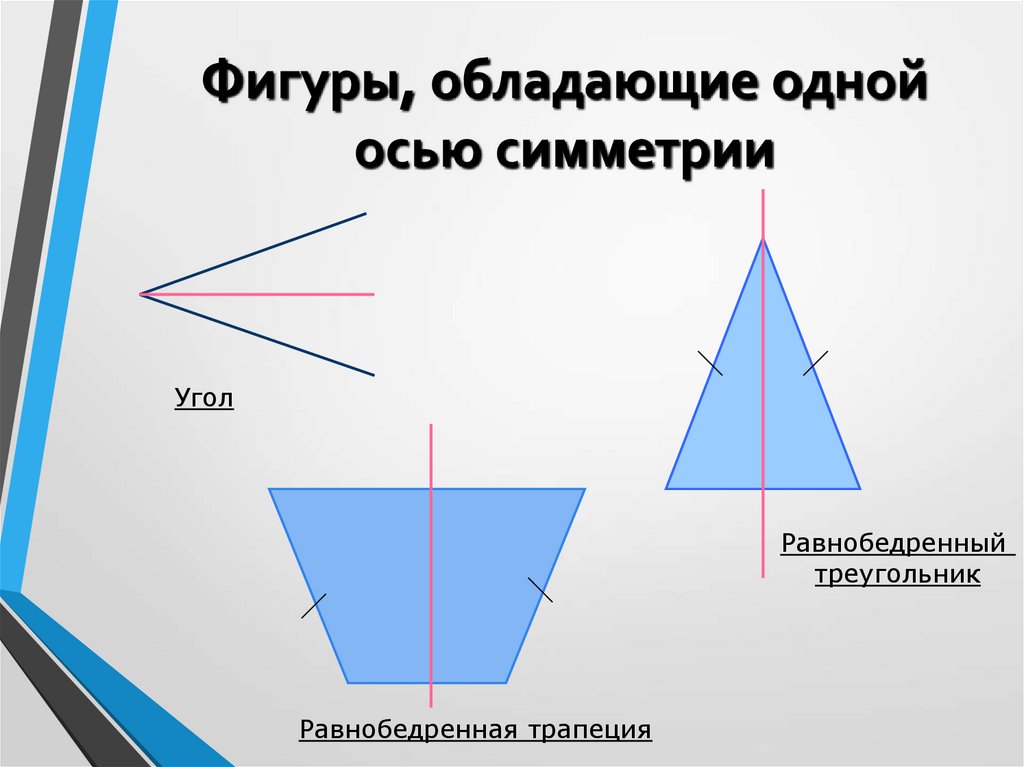
4. Фигуры, обладающие одной осью симметрии
УголРавнобедренный
треугольник
Равнобедренная трапеция
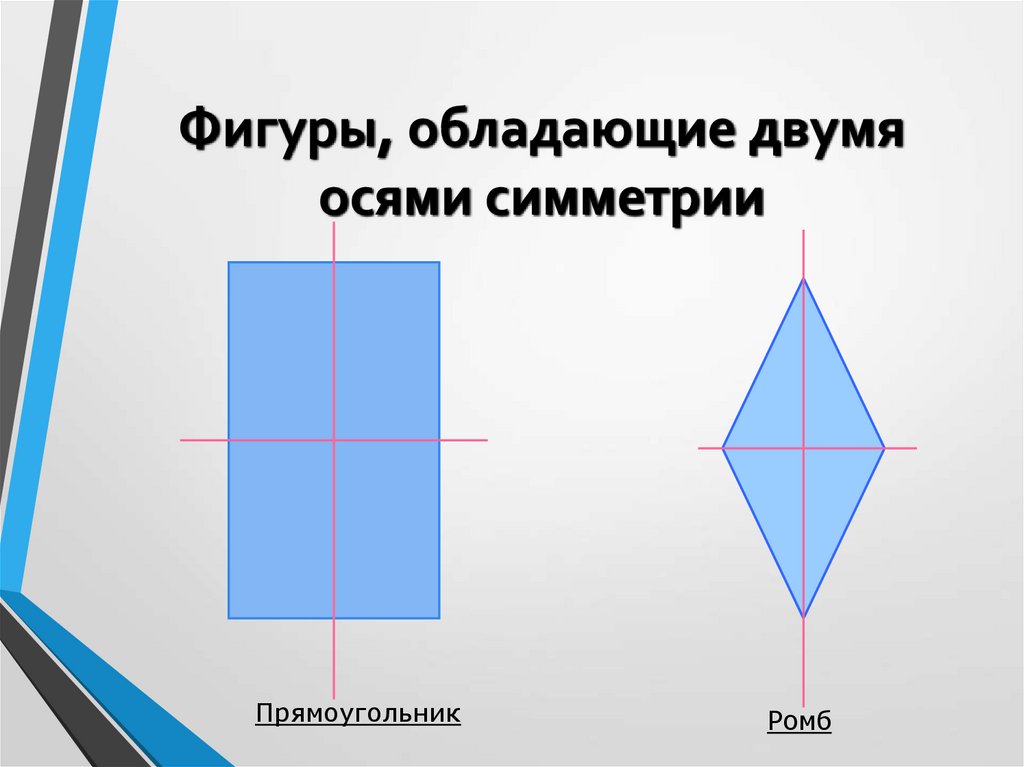
5. Фигуры, обладающие двумя осями симметрии
ПрямоугольникРомб
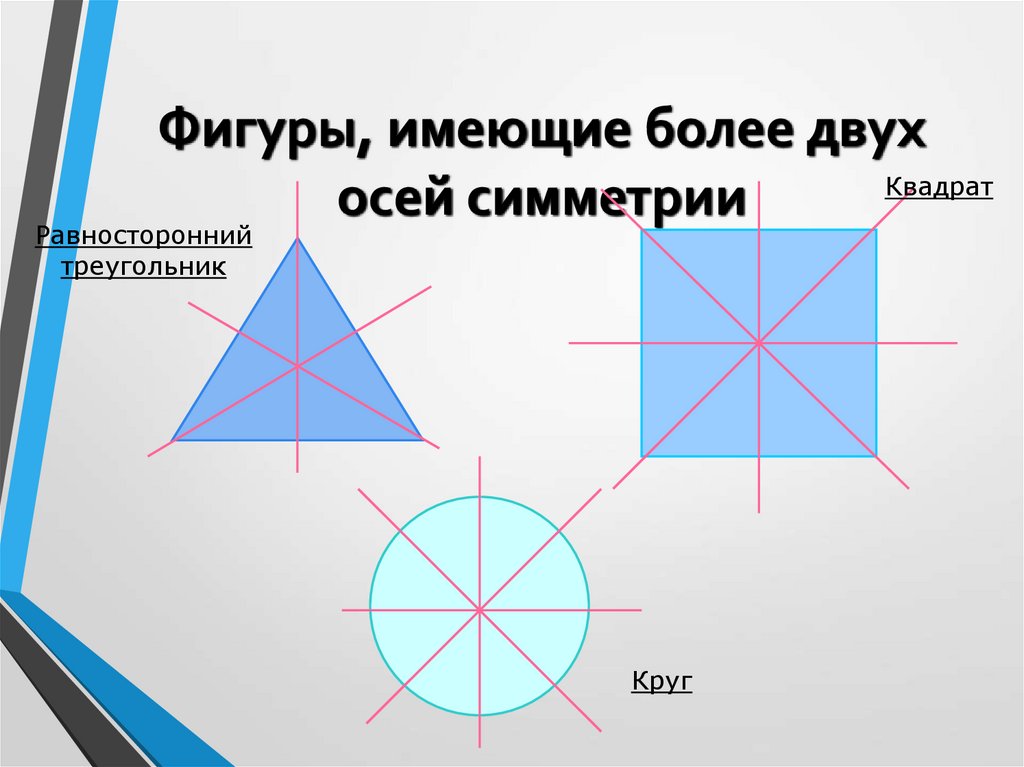
6. Фигуры, имеющие более двух осей симметрии
Фигуры, имеющие более двухКвадрат
осей симметрии
Равносторонний
треугольник
Круг
7. Фигуры, не обладающие осевой симметрией
Произвольныйтреугольник
Параллелограмм
Неправильный
многоугольник
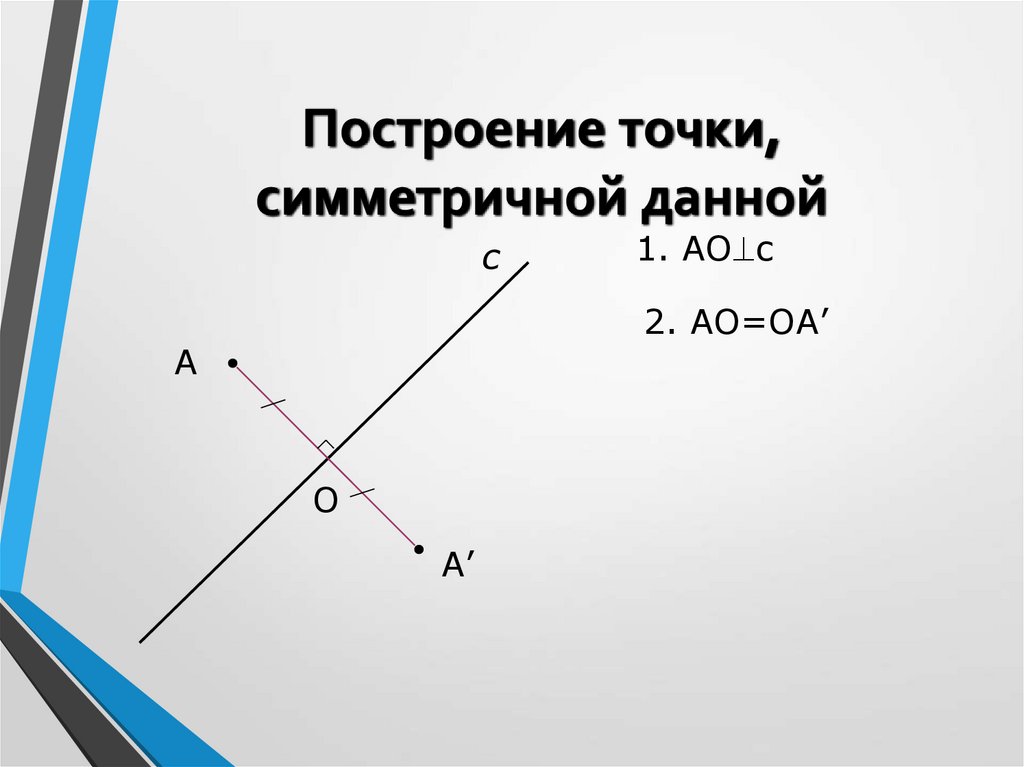
8. Построение точки, симметричной данной
с1. АО с
2. АО=ОА’
А
О
А’
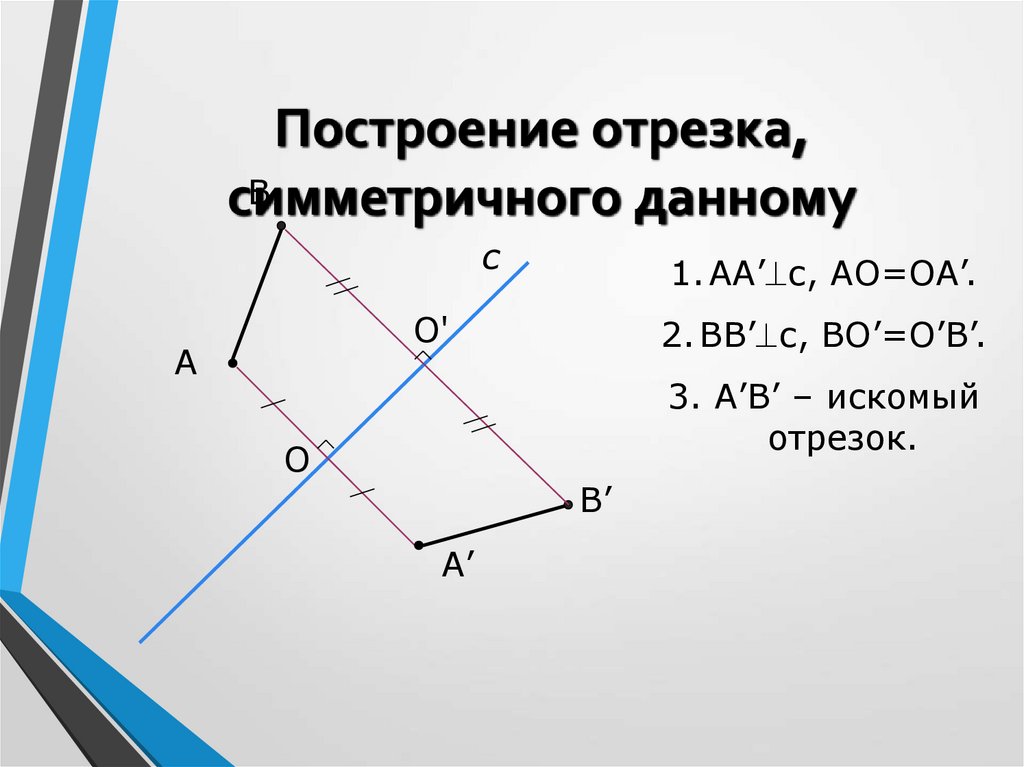
9. Построение отрезка, симметричного данному
Построение отрезка,В
симметричного
данному
с
1. АА’ с, АО=ОА’.
O'
А
2. ВВ’ с, ВО’=О’В’.
3. А’В’ – искомый
отрезок.
O
В’
А’
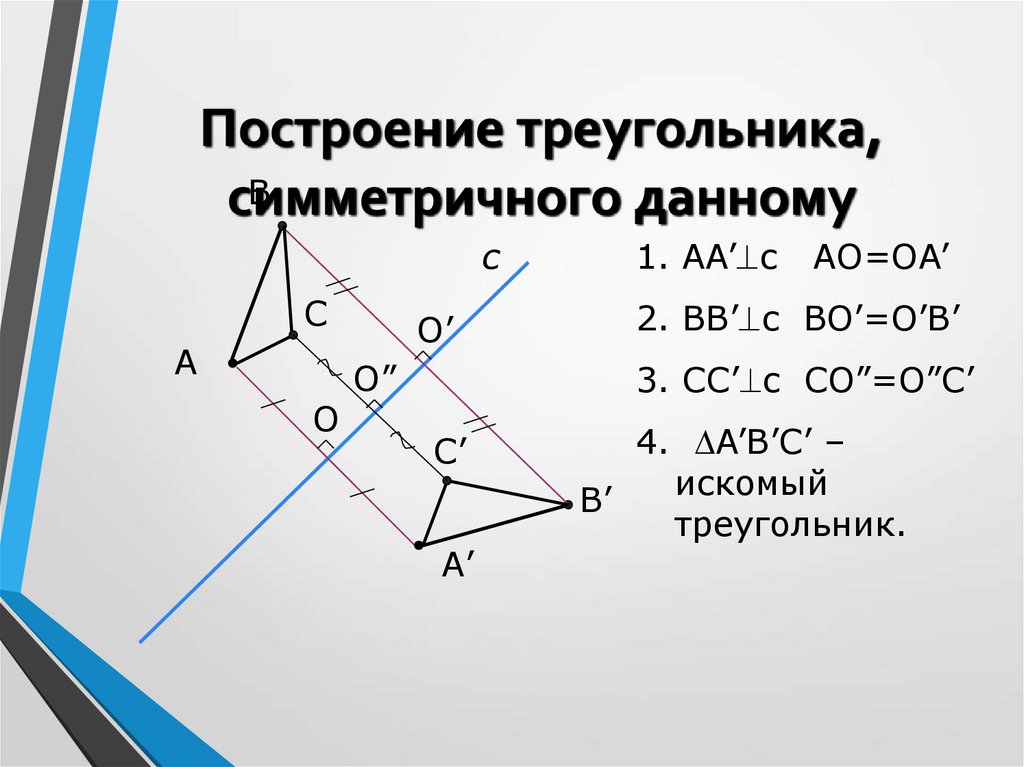
10. Построение треугольника, симметричного данному
Построение треугольника,В
симметричного
данному
с
С
А
O
O’
O”
1. AA’ c
AO=OA’
2. BB’ c BO’=O’B’
3. СС’ c СO”=O”С’
С’
А’
4. A’B’С’ –
искомый
В’
треугольник.
11. Симметрия в природе
12. В архитектуре
13. Симметрия в искусстве
14. Симметрия в поэзии
Пушкин А.С. «Медный всадник»…В гранит оделася Нева;
Мосты повисли над водами;
Темнозелеными садами
Ее покрылись острова…







 mathematics
mathematics








