Similar presentations:
Структура теоремы. Импликативная и категорическая формы теоремы
1.
СТРУКТУРА ТЕОРЕМЫ.ИМПЛИКАТИВНАЯ И
КАТЕГОРИЧЕСКАЯ ФОРМЫ
ТЕОРЕМЫ
Работу
выполнила Бут
София
Евгеньевна
Направлениедизайн
интерьера
Б-3101
2.
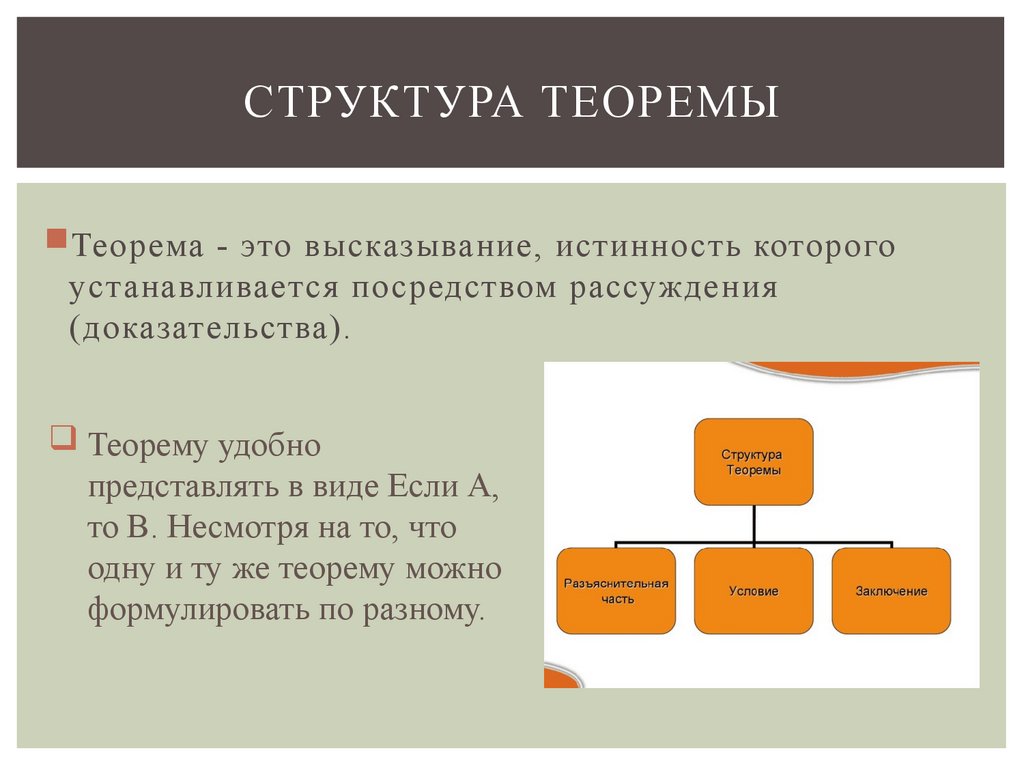
СТРУКТУРА ТЕОРЕМЫТеорема - это высказывание, истинность которого
устанавливается посредством рассуждения
(доказательства).
Теорему удобно
представлять в виде Если А,
то В. Несмотря на то, что
одну и ту же теорему можно
формулировать по разному.
3.
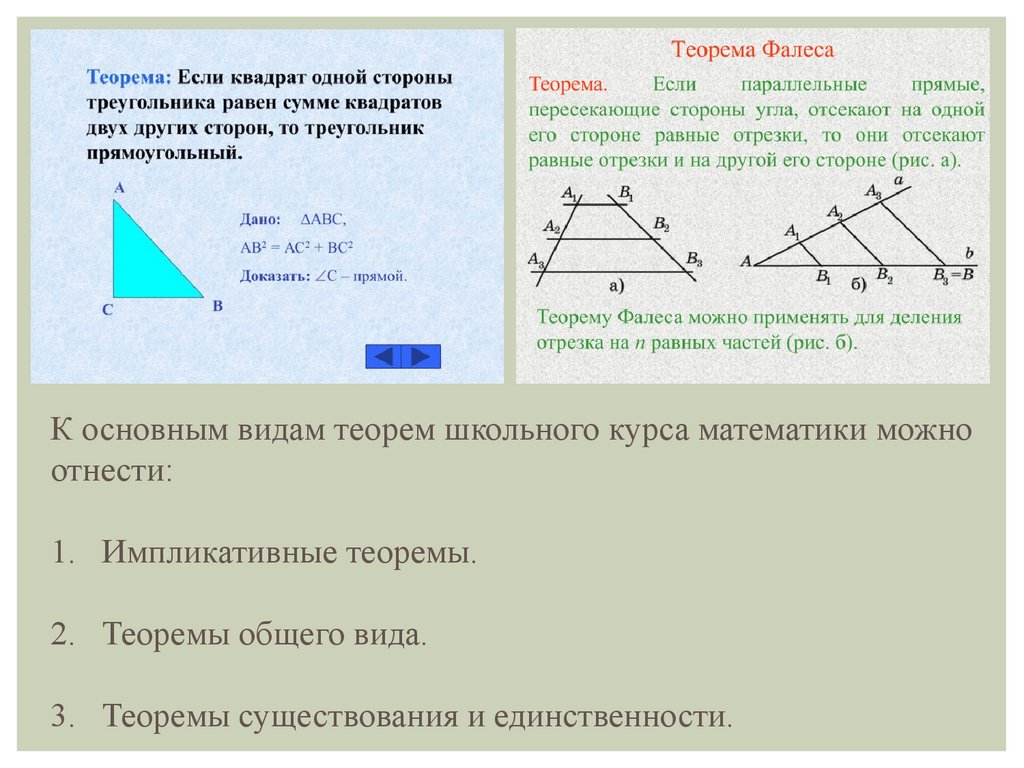
К основным видам теорем школьного курса математики можноотнести:
1. Импликативные теоремы.
2. Теоремы общего вида.
3. Теоремы существования и единственности.
4.
А ⇒В – это данная (прямая) теоремаВсе кладут сначала в рот
Бутерброд,
А потом едят компот.
Он всегда наоборот!
Он сначала ест компот
За компотом – бутерброд.
В ⇒А – обратноеутверждение (теорема)
( А Барто «Мальчик наоборо
5.
ИМПЛИКАТИВНАЯ ИКАТЕГОРИЧЕСКАЯ ФОРМЫ ТЕОРЕМЫ
Импликативная и категорическая- это виды
формулировок
Теорема может быть
сформулирована в
категорической форме и в
условной форме.
6.
ПРИМЕРЫНапример, условием теоремы «если четырехугольник
является прямоугольником, то в нем диагонали
равны» является предложение «четырехугольник прямоугольник», а заключением - предложений «в
таком четырехугольнике диагонали равны».
Дана теорема «если число делится на 3 и 4, то оно
делится на 12». Предложение, противоположное
данному, можно сформулировать так: «если число не
делится на 12, то оно не делится на 3 или не делит с я
на 4».
7.
ПРИМЕРЫЕсли автобус придет вовремя, то я вовремя приеду
до конечной остановки.
Если я своевременно не буду делать домашнее
задание, то трудно будет получить хороший балл и
репутацию.
8.
ТЕЗИСЫВ том случае, если предложение, обратное данному,
будет истинно, его называют теоремой, обратной
данной.
Предложение, обратно противоположное какой-либо
теореме, также является теоремой, и, значит, вместо
данной теоремы можно доказывать теорему, обратно
противоположную данной.
Теорема представляет собой высказывание вида А
В, где А и В - высказывательные формы с одной или
несколькими переменными. Предложение А называют
условием теоремы, а предложение В - ее
заключением.
9.
ТЕЗИСЫПоэтому контрапозиционное утверждение к теореме
всегда является истинным. Его можно назвать
теоремой. Утверждение, обратное к теореме, не
всегда является истинным.
Ложность утверждения с квантором общности можно
доказать, отыскав контрпример, а истинность
доказывается путём рассуждений, проведённых для
произвольного элемента х из множества М.
10.
СПИСОК ИСПОЛЬЗОВАННОЙЛИТЕРАТУРЫ
Upload Теоремы и их доказательства / Upload. —
Текст : электронный // StudFiles : [сайт]. — URL:
(дата обращения: 11.09.2023).
Upload Структура теоремы. Виды теорем / Upload. —
Текст : электронный // StudFiles : [сайт]. — URL:
(дата обращения: 11.09.2023).
11.
ГЛОССАРИЙИмпликативная и категорическая- это виды
формулировок.
Теорема - это высказывание, истинность
которого устанавливается посредством
рассуждения (доказательства).
Структура теоремы- это разъяснительная, условие и
заключение.
12.
íàéäè ñëîâà.pdf13.
14.
15.
СТРУКТУРА ТЕОРЕМЫ.ИМПЛИКАТИВНАЯ И
КАТЕГОРИЧЕСКАЯ ФОРМЫ
ТЕОРЕМЫ
Работу
выполнила Бут
София
Евгеньевна
Направлениедизайн
интерьера
Б-3101













 mathematics
mathematics