Четырехугольник и его элементы

1. ЧЕТЫРЕХУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ

2.

Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать!
Например, в фигуре этой
Сколько разных?
Рассмотри!
Все внимательно исследуй
И “по краю” и “внутри”.
Это интересно
Повторяем

3.

Это интересно
Треугольник – простейшая фигура:
три
Через
стороны,
площадь
тритреугольника
вершины,
три
Император
Франции
Наполеон
Особенно плодотворно свойства
Через
угла.
выражается
Математики
2000 летвремя
площадь
в Древней
называют
любого
Греции
его
свободное
посвящал
треугольника
Еще 4000 лет
исследовались
назад в одном
в XVочень
двумерным
многоугольника,
активно
“симплексом”
велось
достаточно
изучение
- по
занятиям
математикой
египетском
XVI
веках. папирусе
Большой
говорилось
вклади,ввэтуо
свойств
разбить
латыни
треугольника.
этот
означает
многоугольник
простейший.
Пифагор
на
частности,
изучению
свойств
теорию
площади
внес знаменитый
треугольника.
математик
открыл
Именно
треугольники,
свою
в силу
знаменитую
своей
вычислить
простоты
формулу.
их
треугольников.
Леонард Эйлер.
треугольник
площади и явился
сложить
основой
результаты.
многих
измерений.
1
2
3
4
5
6

4.

• Треугольник – это геометрическая фигура, которая
состоит из …
• Элементами треугольника являются…
• Какие виды треугольников вы знаете?
• При каких условиях треугольники равны?
• Сформулировать признаки равенства треугольников
вы знаете?

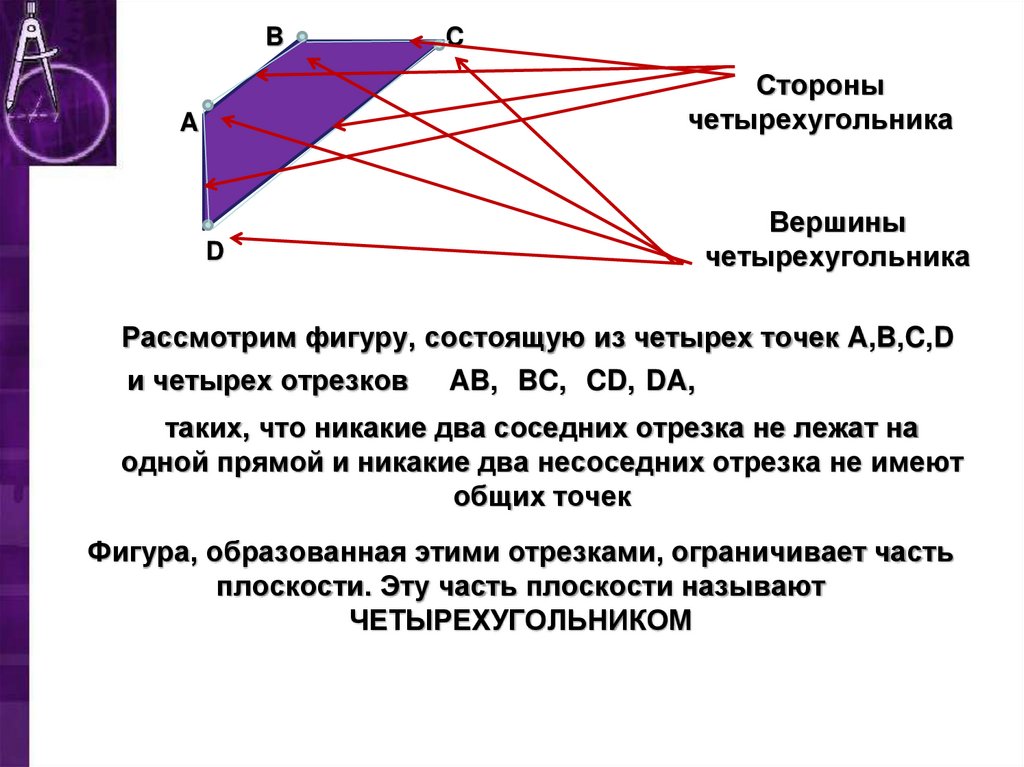
5. Рассмотрим фигуру, состоящую из четырех точек A,B,C,D

B
C
Стороны
четырехугольника
A
D
Вершины
четырехугольника
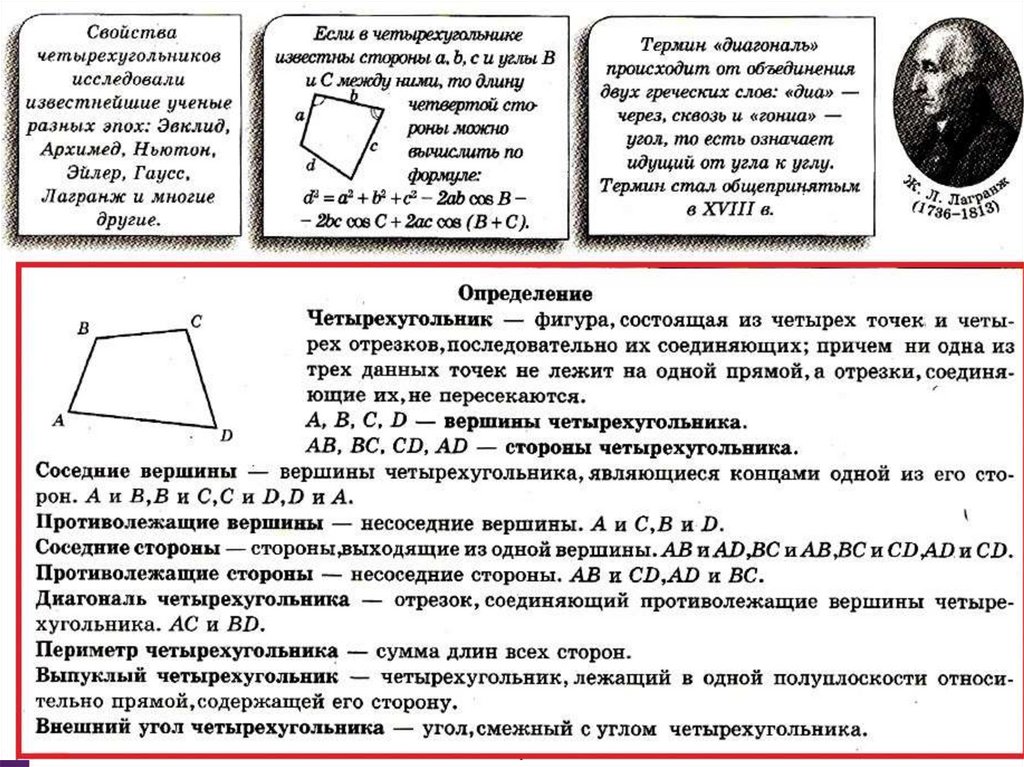
Рассмотрим фигуру, состоящую из четырех точек A,B,C,D
и четырех отрезков AB, BC, CD, DA,
таких, что никакие два соседних отрезка не лежат на
одной прямой и никакие два несоседних отрезка не имеют
общих точек
Фигура, образованная этими отрезками, ограничивает часть
плоскости. Эту часть плоскости называют
ЧЕТЫРЕХУГОЛЬНИКОМ

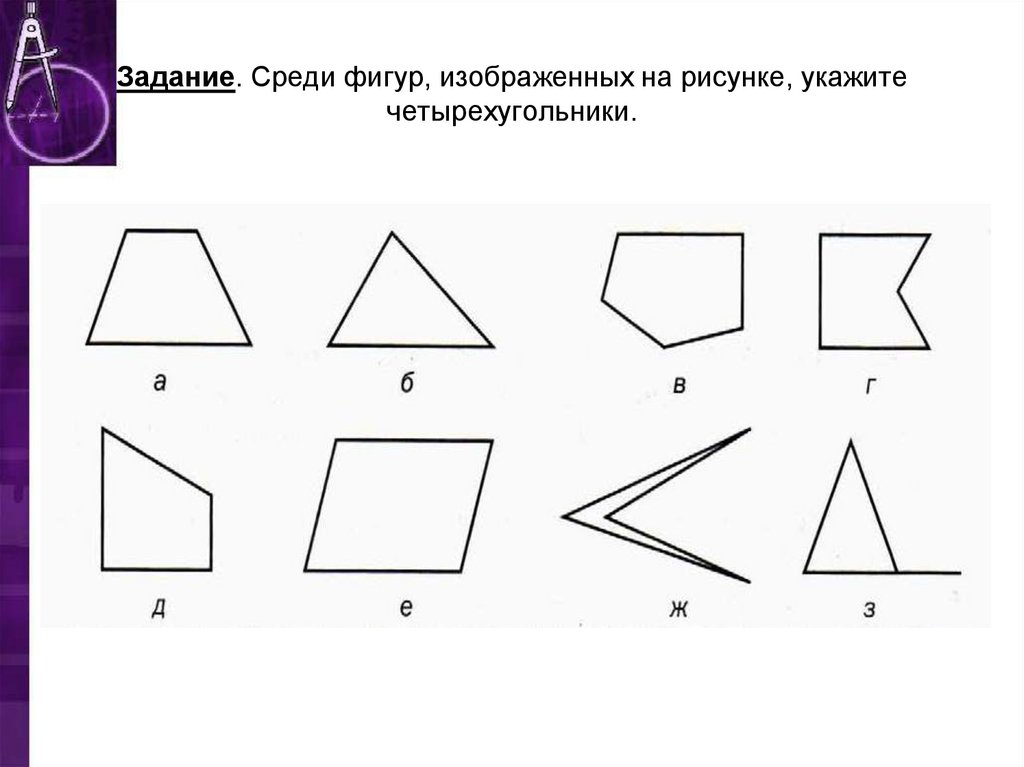
6. Задание. Среди фигур, изображенных на рисунке, укажите четырехугольники.

7. Стороны четырехугольника, являющиеся соседними отрезками, называются соседними сторонами четырехугольника

Отрезок, соединяющий противолежащие
вершины четырехугольника, называют
диагональю четырехугольника
Стороны четырехугольника, являющиеся соседними отрезками,
называются соседними сторонами четырехугольника
Вершины четырехугольника, являющиеся концами одной стороны,
называют соседними вершинами четырехугольника
Стороны четырехугольника, не являющиеся соседними, называют
противолежащими сторонами четырехугольника
Несоседние вершины четырехугольника, называют
противолежащими вершинами четырехугольника

8. Укажите: 1.вершины четырехугольника

Задание.
Назовите 2 каких-нибудь обозначения четырехугольника.
Укажите:
1.вершины четырехугольника
2.стороны четырехугольника
3.пары соседних вершин
4.пары противолежащих вершин
5.пары соседних сторон
6.пары противолежащих сторон
7. диагонали четырехугольника

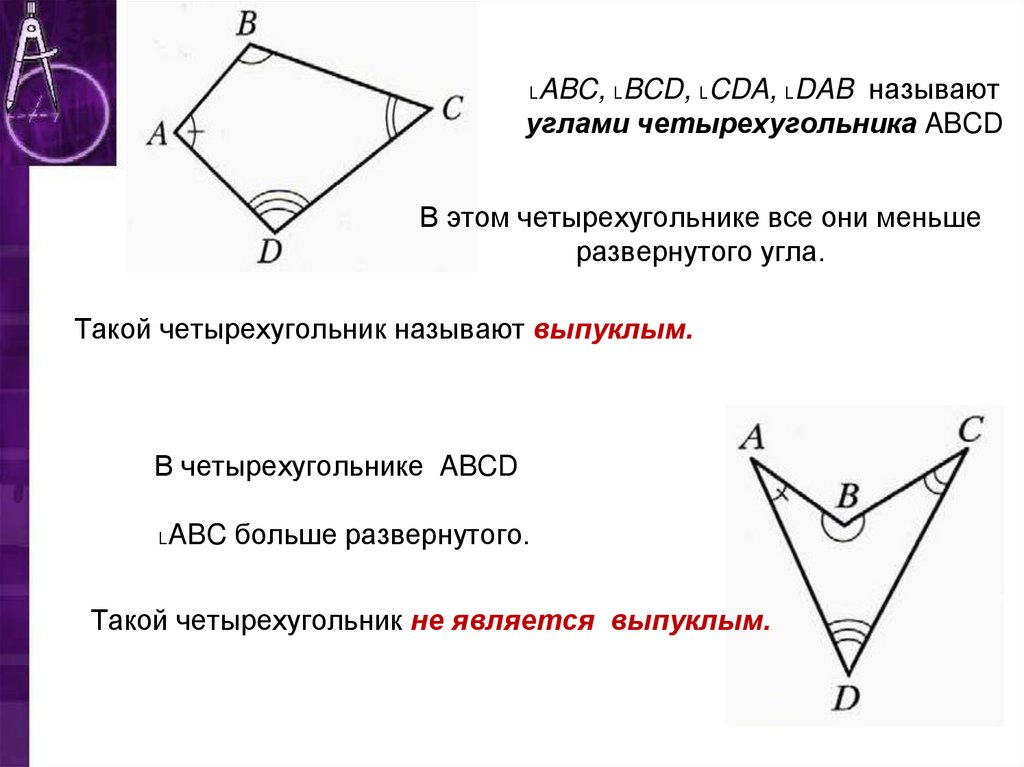
9. ˪ABC, ˪BCD, ˪CDA, ˪DAB называют углами четырехугольника ABCD

В этом четырехугольнике все они меньше
развернутого угла.
Такой четырехугольник называют выпуклым.
В четырехугольнике ABCD
˪ABC больше развернутого.
Такой четырехугольник не является выпуклым.

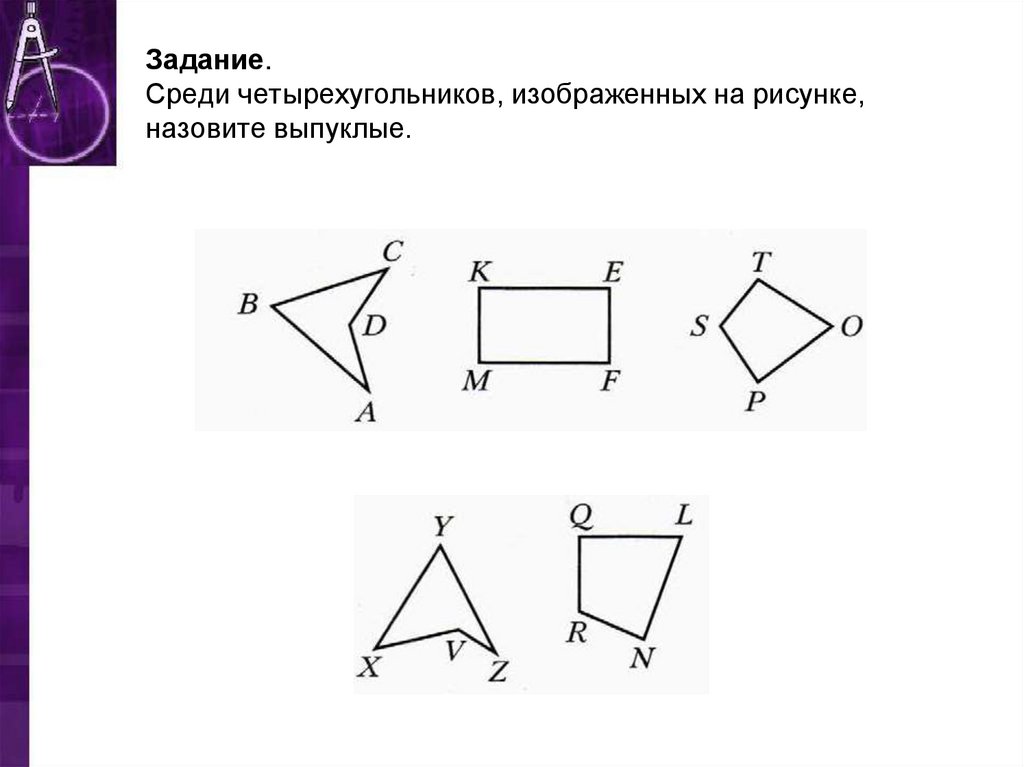
10. Задание. Среди четырехугольников, изображенных на рисунке, назовите выпуклые.

11.

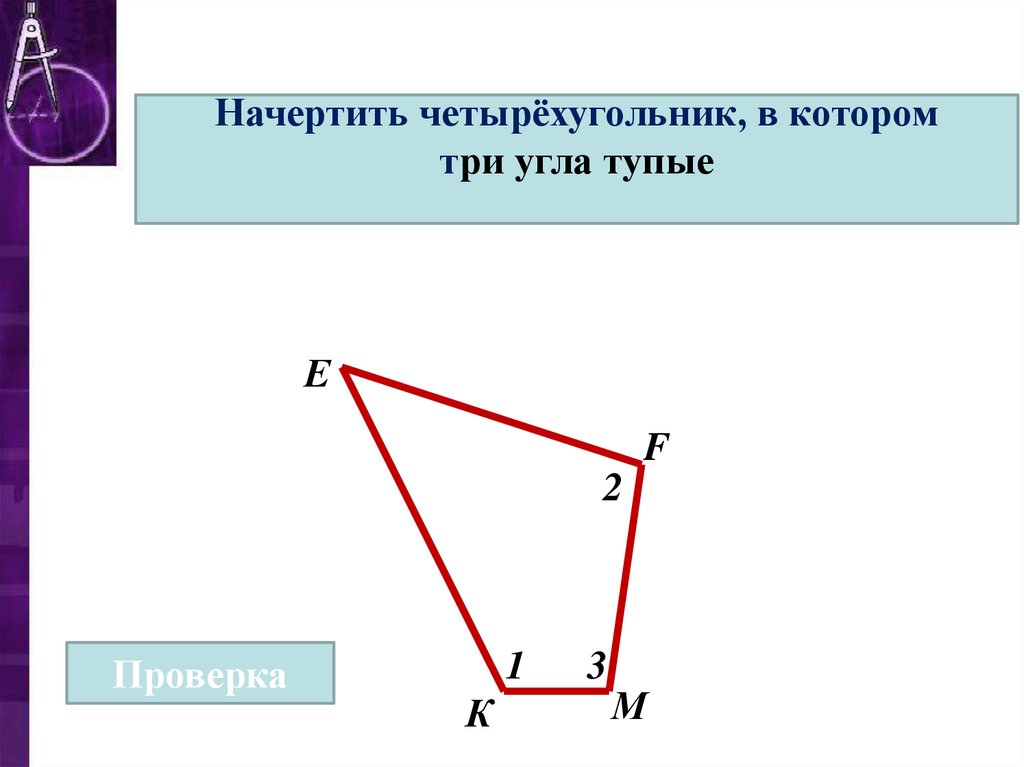
Начертить четырёхугольник, в котором
три угла тупые
Е
F
2
Проверка
1
К
3
М

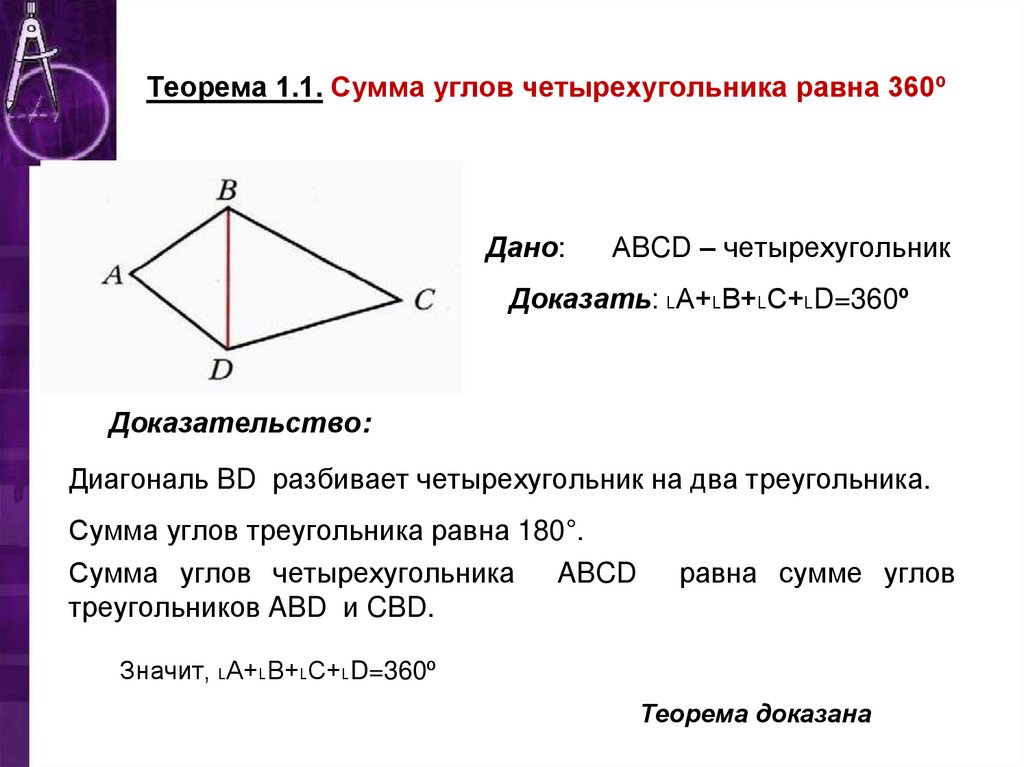
12. Теорема 1.1. Сумма углов четырехугольника равна 360º

Дано:
АBCD – четырехугольник
Доказать: ˪А+˪В+˪С+˪D=360º
Доказательство:
Диагональ BD разбивает четырехугольник на два треугольника.
Сумма углов треугольника равна 180°.
Сумма углов четырехугольника ABCD
треугольников ABD и CBD.
равна сумме углов
Значит, ˪А+˪В+˪С+˪D=360º
Теорема доказана

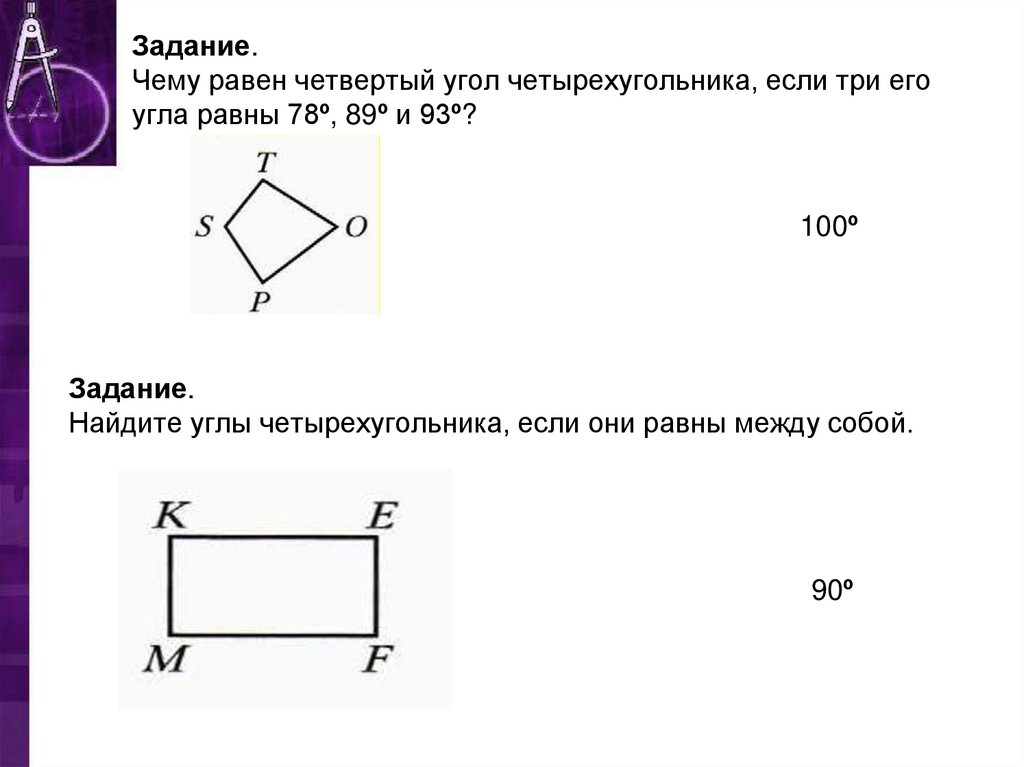
13. Задание. Чему равен четвертый угол четырехугольника, если три его угла равны 78º, 89º и 93º?

100º
Задание.
Найдите углы четырехугольника, если они равны между собой.
90º

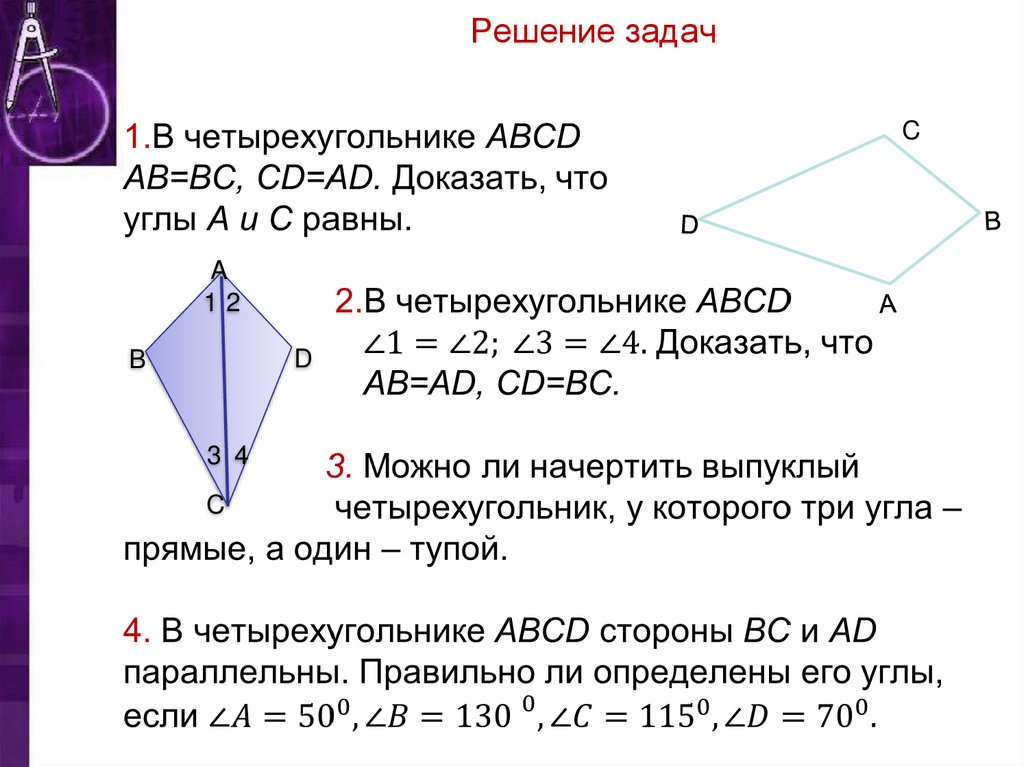
14. Решение задач

C
A
12
D
B
3 4
C

15. Следствие. В четырехугольнике только один из углов может быть больше развернутого

Задача.
Может ли у четырехугольника быть:
три прямых угла и один острый;
три прямых угла и один тупой;
четыре прямых угла;
четыре острых угла;
два прямых и два тупых угла;
два прямых угла, один острый и один тупой?

16.

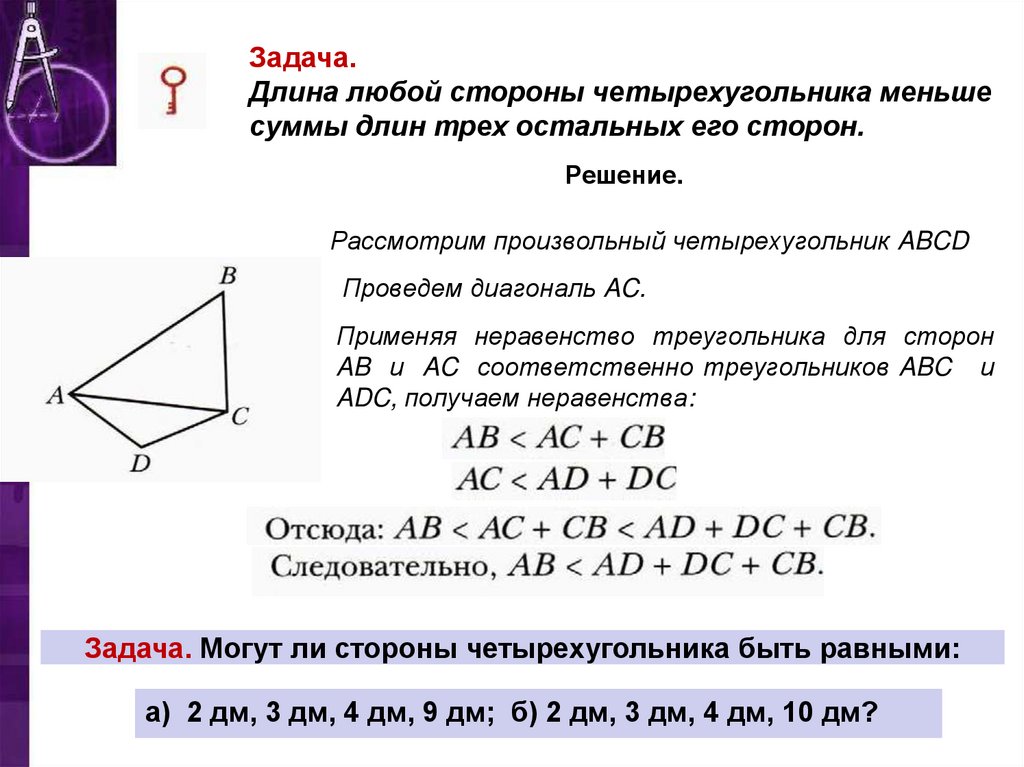
Задача.
Длина любой стороны четырехугольника меньше
суммы длин трех остальных его сторон.
Решение.
Рассмотрим произвольный четырехугольник ABCD
Проведем диагональ AC.
Применяя неравенство треугольника для сторон
AB и AC соответственно треугольников ABC и
ADC, получаем неравенства:
Задача. Могут ли стороны четырехугольника быть равными:
а) 2 дм, 3 дм, 4 дм, 9 дм; б) 2 дм, 3 дм, 4 дм, 10 дм?