Similar presentations:
Изображение пространственных фигур
1.
Изображениепространственных фигур.
2.
Рассмотрим теперь изображения наплоскости некоторых многогранников
при условии,что ни одна из плоскостей
граней не параллельна направлению
проектирования. При этом под
изображением многогранника будем
понимать фигуру, состоящую из
проекций всех ребер.
3.
Тетраэдр.Пусть А”B”C”D”- произвольный тетраэдр, B”B”C”D”- произвольный тетраэдр, C”B”C”D”- произвольный тетраэдр, D”B”C”D”- произвольный тетраэдр, - произвольный тетраэдр,
A, B, C, D- параллельные проекции его
вершин на плоскость изображений.
Отрезки AB, BC, CA, AD, BD, CD служат
сторонами и диагоналями
четырехугольника ABCD. Фигура,
образованная из этих отрезков( или люб.
др., подобная ей), является изображением
тетраэдра A”B”C”D”- произвольный тетраэдр, B”B”C”D”- произвольный тетраэдр, C”B”C”D”- произвольный тетраэдр, D”B”C”D”- произвольный тетраэдр, . Можно доказать,что
фигура, состоящая из сторон и диагоналей
любого ( вып.или невып.) чет-ника, явл.
Изображением тетраэдра при
соответствующем выборе плоскости
изображений и направления
проетирования.
4.
Параллелепипед.Для построения изобр. Произвольного пар-педа
ABCDA1B1C1D1 заметим, что точки A, B, D и A1
явл.вершинами тетраэдра ABDA1. Поэтому в
качестве их изображения можно взять вершины
произвольного чет-ника ABDA1. Другими
словами , любые три отрезка AB, AD и AA1
плоскости изоб. С общим концом А, никакие два
из которых не лежат на одной прямой, можно
считать изоб.ребер AB, AD и AA1 пар-педа. Но
тогда изображения остальных ребер строятся
однозначно, т.к. Все грани пар-педа явл.
Параллелограммами, и, следовательно их
изображения также буду параллелограммами.
5.
Пирамида.Изображение основания
пирамиды строят по описанным
в п.3 правилам, а за изображение
вершины можно принять любую
точку, не принадлежащую
сторонам изображения
основания.
6.
Замечание.Частным случаем параллельной
проекции фигуры является
прямоугольная проекция.
Прямоугольные проекции широко
используются в техническом черчении.
Какая-либо деталь обычно
проектируется на две плоскостигоризонтальную и вертикальную, и обе
проекции изображаются в плоскости
чертежа.
7.
Правило 1. Изображение линийв
трехмерном пространстве.
Все линии (ребра, высоты, линии сечения),
которые были бы не видны, если бы то, что
мы рисуем, было бы сделано из глины
(например) изображаются индикатором. А
все видные линии – сплошными.
8.
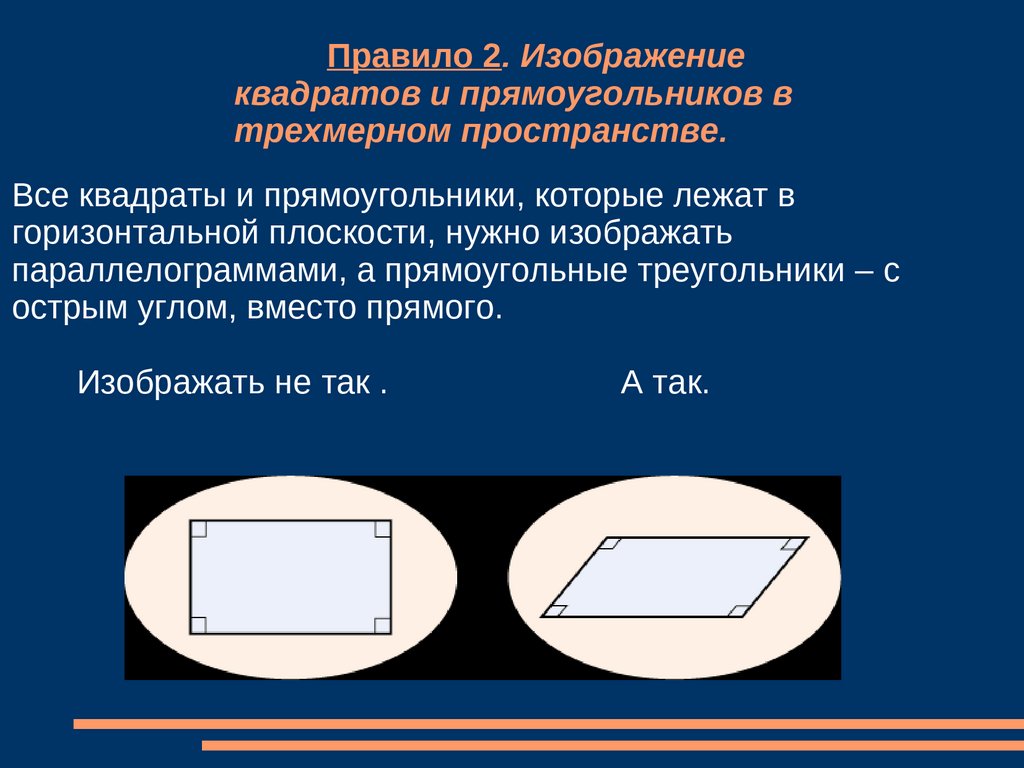
Правило 2. Изображениеквадратов и прямоугольников в
трехмерном пространстве.
Все квадраты и прямоугольники, которые лежат в
горизонтальной плоскости, нужно изображать
параллелограммами, а прямоугольные треугольники – с
острым углом, вместо прямого.
Изображать не так .
А так.
9.
Правило 3. Изображениекругов в трехмерном
пространстве.
Все круги превращаются в овалы (тоже в
горизонтальной плоскости)









 mathematics
mathematics








