Количество информации

1. Количество информации

Уважаемые слушатели курсов повышения квалификации!
В презентации представлены задания, которые необходимо
выполнить.

2.

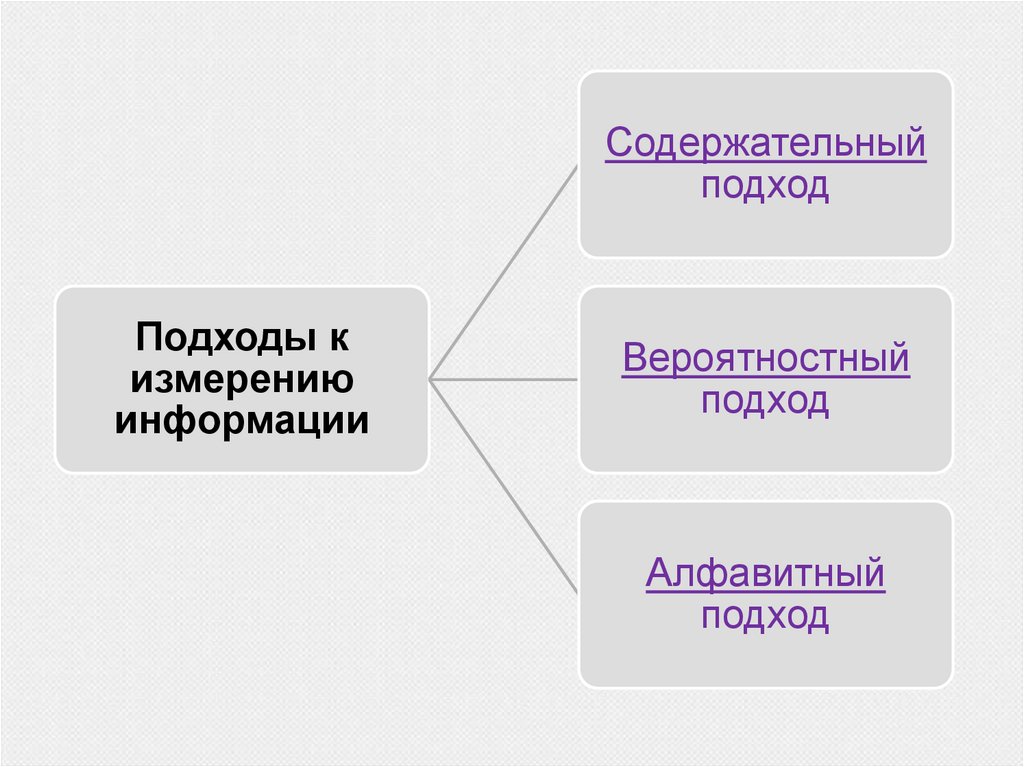
Содержательный
подход
Подходы к
измерению
информации
Вероятностный
подход
Алфавитный
подход

3. ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ

1 байт = 23 бит = 8 бит
1 Кбайт = 210 байт = 1024 байт
1 Мбайт = 210 Кбайт = 1024 Кбайт
1 Гбайт = 210 Мбайт = 1024 Мбайт

4.

СОДЕРЖАТЕЛЬНЫЙ ПОДХОД
Сообщение информативно, если
в нем содержатся новые и
понятные сведения.
Чем больше информативность,
тем большее количество
информации содержится в
сообщении.

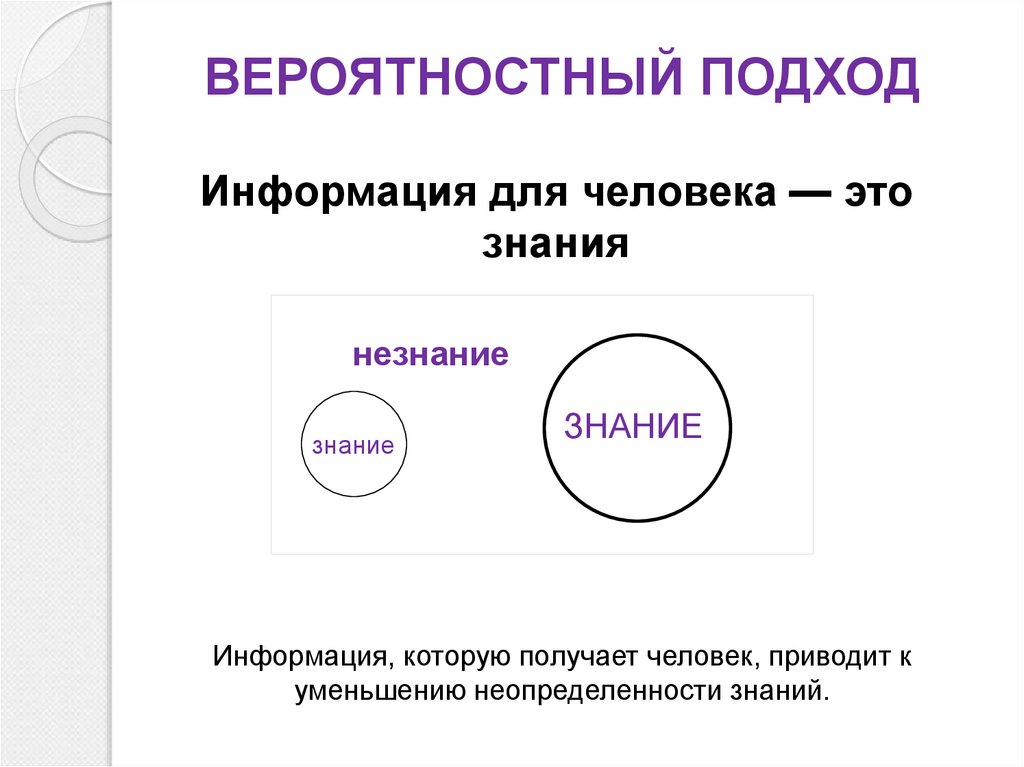
5. ВЕРОЯТНОСТНЫЙ ПОДХОД

Информация для человека — это
знания
незнание
знание
ЗНАНИЕ
Информация, которую получает человек, приводит к
уменьшению неопределенности знаний.

6.

События равновероятны, если ни
одно из них не имеет преимущества
перед другим.
Возможные события.
Они равновероятны
Произошедшее событие

7.

Сообщение, уменьшающее
неопределенность знаний
человека в два раза, несет для
него 1 бит информации.

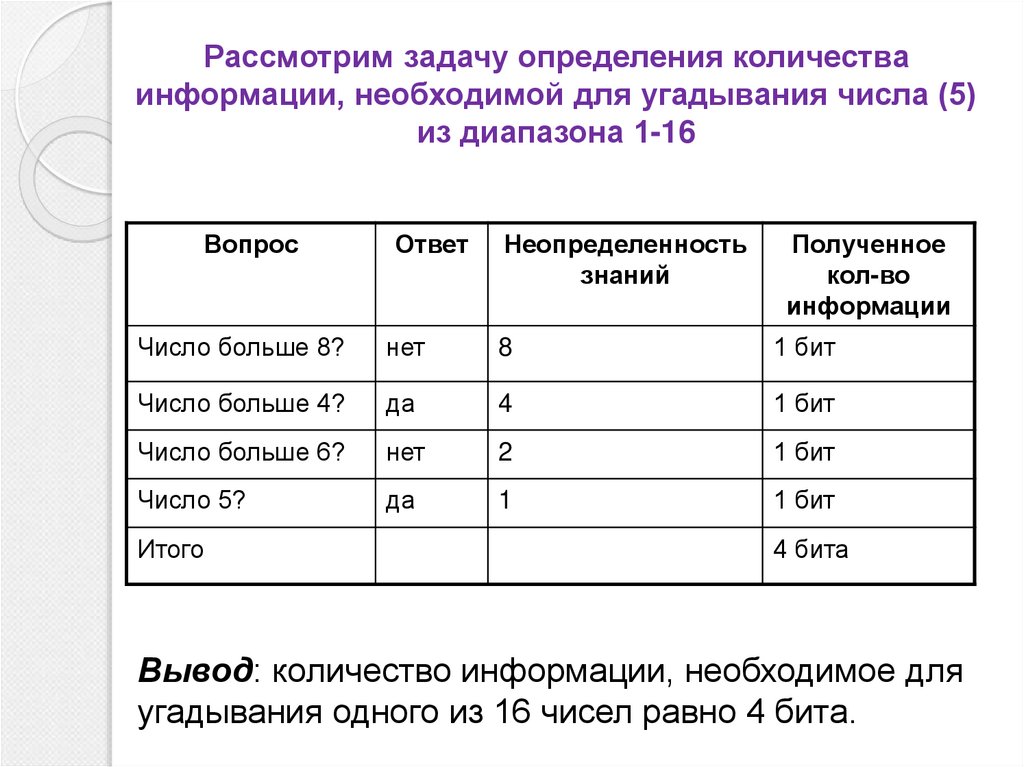
8. Рассмотрим задачу определения количества информации, необходимой для угадывания числа (5) из диапазона 1-16

Вопрос
Ответ
Неопределенность
знаний
Полученное
кол-во
информации
Число больше 8?
нет
8
1 бит
Число больше 4?
да
4
1 бит
Число больше 6?
нет
2
1 бит
Число 5?
да
1
1 бит
Итого
4 бита
Вывод: количество информации, необходимое для
угадывания одного из 16 чисел равно 4 бита.

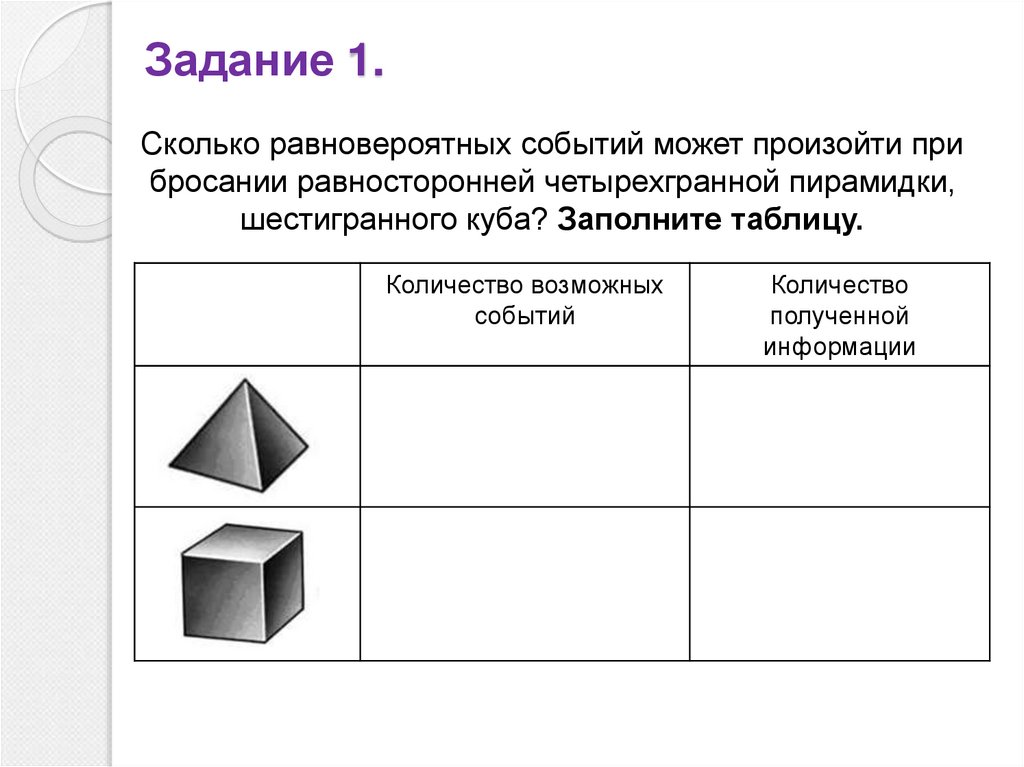
9. Задание 1.

Сколько равновероятных событий может произойти при
бросании равносторонней четырехгранной пирамидки,
шестигранного куба? Заполните таблицу.
Количество возможных
событий
Количество
полученной
информации

10. ФОРМУЛЫ:

Формула Хартли (получена в 1928 году).
i log 2 N
i – количество информации
N – количество равновероятных
событий

11. ФОРМУЛЫ:

K
Р
N
1
i log 2
P
N – общее число возможных исходов какого-то
процесса
К – сколько раз может произойти интересующее
событие
Р – вероятность этого события
Количественная зависимость между
вероятностью события (Р) и количеством
информации (i) в сообщении о нем.
Количеством информации для событий с разными
вероятностями.
N
i Pi log 2 Pi
i 1
Формула Шеннона

12. Задание 2.

Вычислите количество
информации в сообщении о том,
что из колоды карт случайным
образом достали туз червей.

13. Задание 3.

Сколько бит информации несет
сообщение о том, что из колоды в 32 карты
достали даму пик?
Сколько информации несет сообщение
о том, что достали карту черной масти?
Сколько информации несет сообщение
о том, что достали карту бубновой масти?

14.

ЗАДАЧА.
Сообщение о том, что ваш друг живет
на десятом этаже несет в себе 4 бита
информации. Сколько этажей в доме?
РЕШЕНИЕ:
i
N=2
i = 4 бита
N = 24 = 16
Ответ: 16 этажей в доме.

15.

ЗАДАЧА.
Какое количество информации о цвете вынутого шарика
будет получено, если в непрозрачном пакете хранятся:
10 белых, 20 красных, 30 синих и 40 зеленых шариков?
N
i Pi log 2 Pi
i 1
РЕШЕНИЕ:
N = 10+20+30+40 = 100
Pбел. = 10/100 = 0,1
Pсин. = 30/100 = 0,3
Pкрасн. = 20/100 = 0,2
Pзел. = 40/100 = 0,4
i (0.1 log 2 0.1 0.2 log 2 0.2 0.3 log 2 0.3 0.4 log 2 0.4) 1.85
Ответ: 1,85 бит

16. Задание 4.

Заполните пропуски числами:
5 Кбайт = __ байт = __ бит
__ Кбайт = __ байт = 12288 бит
__ Кбайт = __ байт = 213 бит
__ Гбайт = 1536 Мбайт = __ Кбайт
512 Кбайт = 2? байт = 2? бит

17.

АЛФАВИТНЫЙ ПОДХОД
Позволяет определить количество
информации в тексте, отвлекаясь от
содержания информации, воспринимая
ее как последовательность знаков.
Алфавит – множество символов,
используемых для записи текста.
Мощность алфавита – полное
количество символов в алфавите.

18.

Если допустить, что все символы алфавита
встречаются в тексте с одинаковой частотой
(равновероятно), то для определения
количества информации можно
воспользоваться формулой:
i
N=2
N – мощность алфавита,
i – количество информации, содержащейся в
одном символе алфавита.

19.

При алфавитном подходе объем
информации (I), содержащейся в
тексте, вычисляется по формуле:
I=К·i
К – количество символов в тексте,
i – информационный «вес» одного
символа.

20.

ЗАДАЧА
Для русского алфавита (без буквы ё):
Мощность алфавита (количество равновероятных
событий) N = 32,
Найти количество информации i, которое несет
каждый символ алфавита.
РЕШЕНИЕ:
i
32 = 2
i = 5 бит
Ответ: каждый символ алфавита несет 5 бит
информации.

21. Задание 5.

Какое количество
информации несет один
символ алфавита мощностью
2, 4, 8, 16, 256 символов?

22. Литература:

1.
Козырев А.К., Александрова Н.А., Феоктистова О.А.
Теоретические основы информатики и микроэлектроники: Учебнометодическое пособие для ВУЗов. Саратов: Издательство
«Научная книга», 2012. – 300 с.
2.
Гданский Н.И. Информатика. Профильный уровень: практикум для
10-11 классов: в 2 ч. Ч. 1 / Н.И. Гданский, А.В. Карпов. – М.:
БИНОМ. Лаборатория знаний, 2012. – 429 с.: ил.