Решение уравнений. Система заданий по математике. 6 класс

1.

математики
6 класс
Решение уравнений
Система заданий по теме
Учитель математики
Гладких Н.М.

2.

Раскрытие
скобок

3.

Заполните пропуск в формулировке правил
1. Выражение a+(b+c) можно записать a+b+c. Эту операцию в
раскрытием скобок
математике называют…………………………..
2. Если перед скобками стоит знак «+», то можно опустить скобки
сохранив
и этот знак «+»,
…………… знаки слагаемых, стоящих в скобках.
Если первое слагаемое в скобках записано без знака, то его надо
со знаком плюс
записать ……………………
3. Чтобы раскрыть скобки, перед которыми стоит знак «-», надо
поменяв
заменить этот знак на «+»,…………….
знаки всех слагаемых в
на
противоположные
скобках …………………………..........., а потом раскрыть скобки.
4. Чтобы записать сумму, противоположную сумме нескольких
изменить знаки
слагаемых, надо …………………………....
данных слагаемых.
5. Раскрытие скобок и применение переместительного и
упрощать
сочетательного свойств сложения позволяют ……………..
рационально выполнять
выражения и ……………………………………...
вычисления.

4.

Верно ли раскрыты скобки?
Найди ошибки, обоснуй свой ответ.
а
)
(
12
,
8
b
)
12
,
8
b
;
2
2
б
)
(
b
)
b
;
7
7
в
)
37
(
2
,
9
b
)
37
2
,
9
b
;

5.

Верно ли раскрыты скобки?
Найди ошибки, обоснуй свой ответ.
а
)
(
12
,
8
b
)
12
,
8
b
;
2
2
б
)
(
b
)
b
;
7
7
в
)
37
(
2
,
9
b
)
37
2
,
9
b
;

6.

Верно ли раскрыты скобки?
Найди ошибки, обоснуй свой ответ.
г
)
a
(
125
,
3
t
)
a
125
,
3
t
;

7.

Верно ли раскрыты скобки?
Найди ошибки, обоснуй свой ответ.
г
)
a
(
125
,
3
t
)
a
125
,
3
t
;
3
3
д
)
k
(
b
)
k
b
;
11
11
)
(
a
c
)
(
0
,
81
b
)
a
c
0
,
81
b
;
ж
2
2

8.

Допишите правую часть равенства,
чтобы оно стало буквенной записью
правил раскрытия скобок .
a b c
a b c
b c
b c
a b c
a b c
b c
b c c b

9.

Коэффициент

10.

Ответьте на вопросы
1. Если выражение является произведением числа
и одной или нескольких букв, то это число как
коэффициент
называют?
2. Где обычно пишут коэффициент в выражении?
перед буквенными множителями
3. Какое число считают числовым
- bc
коэффициентом выражения
?
коэффициент равен -1
x
abc
4. Коэффициентом
такого выражения,
какравенили
коэффициент
1
, какое считают число?
коэффициент выражения
24.a Чтобы
( 5b) 0,определить
3c 2
перемножить
числа
, что надо
сначала сделать?

11.

Верно ли записан коэффициент?
Найди ошибки, обоснуй свой ответ.
а
)
12
,
8
b
,
коэффи
т
12
,
8
;
2
2
2
2
б
б
)
)
b
b
,
коэфф
,
коэфф
т
т
;
;
7
7
7
7
в
в
)
)
a
a
2
2
,
9
,
9
b
b
,
коэффи
,
коэффи
т
т
2
1
,
9
;
;

12.

Верно ли записан коэффициент?
Найди ошибки, обоснуй свой ответ.
г
)
t
,коэффиц
т
1
;
д
)
kb
,
коэффиц
та
нет
б
)kb
,коэффици
т
1
;;
в
)
ж
)
a
a
0
,
81
0
,
81
,
коэффи
,
коэффи
т
т
0
,
1
81
;
;

13.

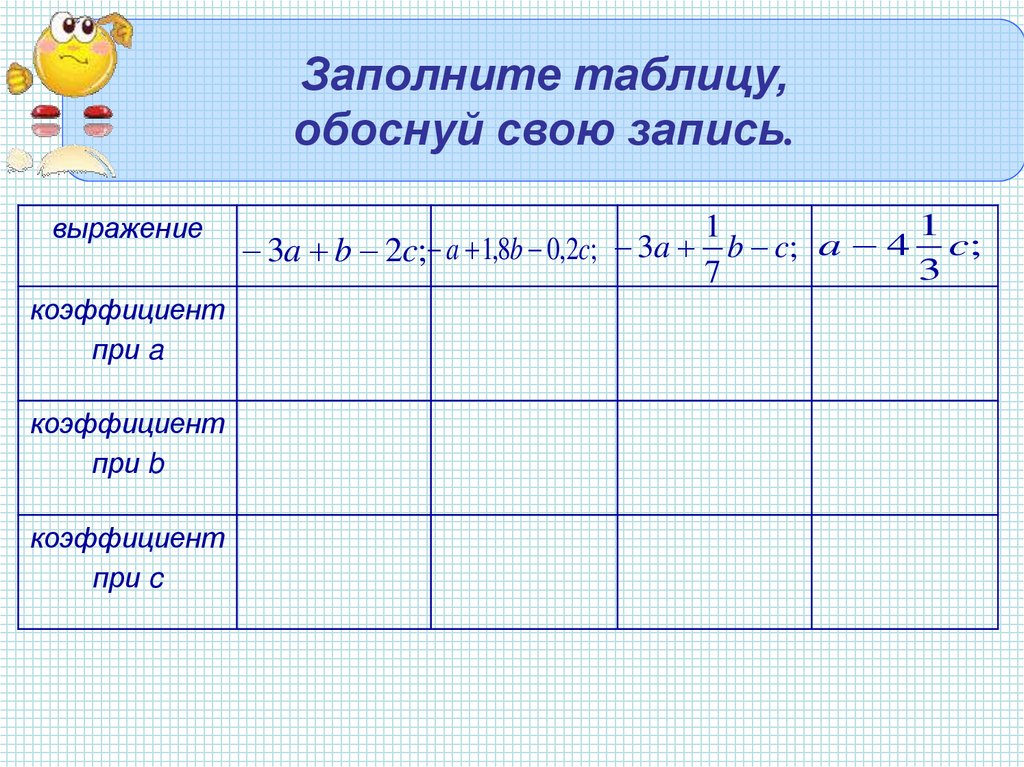
Заполните таблицу,
обоснуй свою запись.
выражение
коэффициент
при a
коэффициент
при b
коэффициент
при c
1
1
a
4
c;
3a b 2c; a 1,8b 0,2c; 3a b c;
3
7

14.

Подобные
слагаемые

15.

Заполните пропуск в формулировке правил
1. Слагаемые, имеющие одинаковую буквенную часть,
называют подобными
………………
2. Чтобы сложить (привести) подобные слагаемые, надо
сложить их коэффициенты и результат умножить
………………………………..………
на общую буквенную часть.
3. Раскрытие скобок и применение правила приведения
подобных слагаемых позволяют ……………….
упрощать и …………………………...........вычисления.
выражения
рационально выполнять

16.

Решение
уравнений

17.

Заполните пропуск в формулировке правил
1. Корень уравнения – это значение переменной,
при котором уравнение превращается в верное равенство
…………………………..
2. Решить уравнение значит ……………………
найти все его корни или доказать, что их нет

18.

Решите уравнение:
7х = 3х + 2;
7х = 3х +2;
7х – 3х = 2;
4х = 2; : 4
х = 0,5;
Ответ: х = 0,5
Решите уравнение:
0,3(63 – х) = 0,4х;
0,3(63 – х) = 0,4х;
18,9 – 0,3х = 0,4х;
–0,3 х – 0,4х = – 18,9;
– 0,7х = – 18,9; : ( 0,7)
х = 27;
Ответ: х = 27

19.

Веревку длиной 63 м разрезали на два куска так,
что 0,4 длины первого куска были равны 0,3 длины
второго куска.
Найдите длину каждого куска верёвки.
Подготовим и заполним таблицу , так как в задаче
говорится о двух кусках верёвки.
Длина, м
Часть длины
Длина части, м
первый
кусок
х
0,4
0,4х
второй
кусок
63 - х
0,3
0,3(63 – х)
По условию часть длины первого куска равна
части длины второго куска.
Составим и решим уравнение.

20.

Веревку длиной 63 м разрезали на два куска так,
что 0,4 длины первого куска были равны 0,3 длины
второго куска.
Найдите длину каждого куска верёвки.
Составим и решим уравнение.
0,3(63 – х) = 0,4х;
18,9 – 0,3х = 0,4х;
–0,3 х – 0,4х = – 18,9;
– 0,7х = – 18,9; : ( 0,7)
Проверка:
27 0,4=10,8(м)
36 0,3= 10,8(м)
длины частей равны,
задачу решили верно
х = 27;
27(м) – длина первого куска веревки
63 – 27 = 36(м) – длина второго куска веревки
Ответ: 27метров и 36метров

21.

Установи порядок действий
при решении задач с помощью уравнений.
Поясни, какие величины нашли.
Сделай проверку по условию задачи.
Прикидкой проверь ответ.
Прочитай внимательно условие задачи.
Ответь на вопрос задачи и запиши ответ задач.
По условию задачи составь уравнение.
Неизвестную величину обозначь за х.
Подготовь таблицу для записи условия задачи.

22.

Установи соответствие.
Словесное выражение
Буквенное
равенство
а=в–7
Число а больше в на 7
а+в=7
а–в=7
Число а больше в в 7 раз
а = 7в
а–7=в
Число а меньше в на 7
а=7–в
7а = в
Число а меньше в в 7 раз
а=в–7
а:в=7
Сумма чисел а и в равна
7
а=в+7
а=в:7
Разность чисел а и в
равна 7
а=7:в