Similar presentations:
Линейная функция
1.
ЛИНЕЙНАЯФУНКЦИЯ
Подготовила учитель математики ВКК Божок
Светлана Петровна МБОУ СОШ №1 с УИОП
г.Воронежа
2016 год
2.
ВИД ФУНКЦИИЛинейная функция имеет вид
y=kx+l
где х - аргумент (независимая переменная),
y – функция, зависящая от х, k и l – любые
числа.
3.
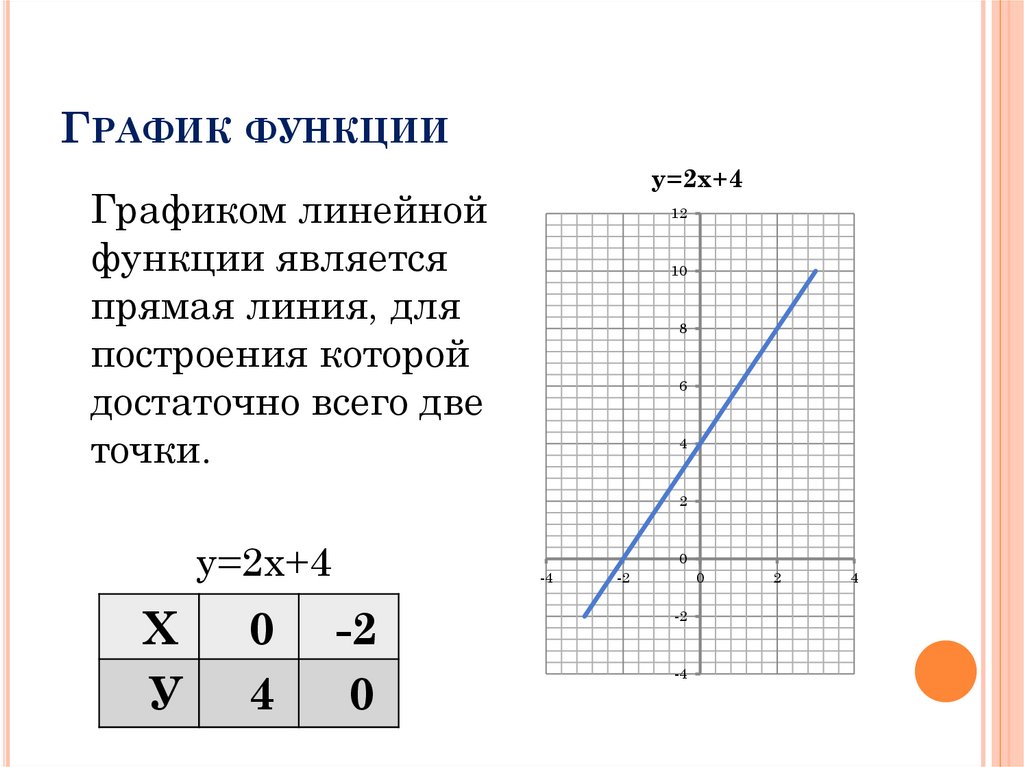
ГРАФИК ФУНКЦИИу=2х+4
Графиком линейной
функции является
прямая линия, для
построения которой
достаточно всего две
точки.
12
10
8
6
4
2
у=2х+4
Х
У
0
4
0
-4
-2
0
-2
0
-2
-4
2
4
4.
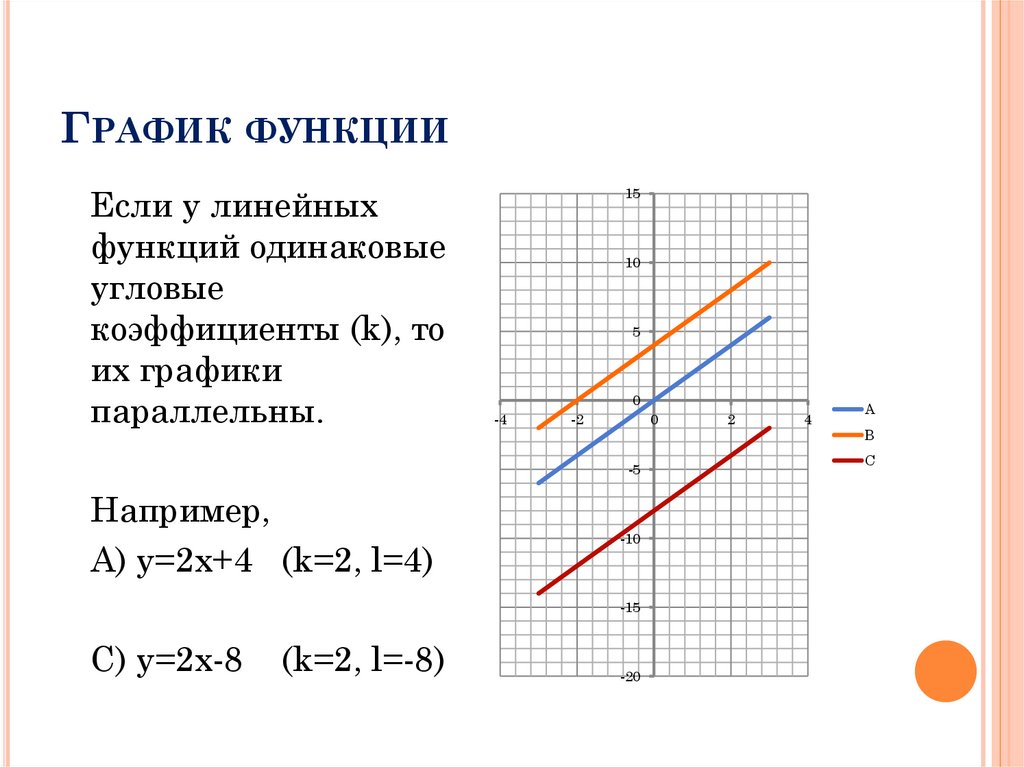
ГРАФИК ФУНКЦИИЕсли у линейных
функций одинаковые
угловые
коэффициенты (k), то
их графики
параллельны.
15
10
5
0
-4
-2
0
-5
Например,
A) y=2x+4 (k=2, l=4)
B) y=2x
(k=2, l=0)
C) y=2x-8 (k=2, l=-8)
-10
-15
-20
2
4
A
B
C
5.
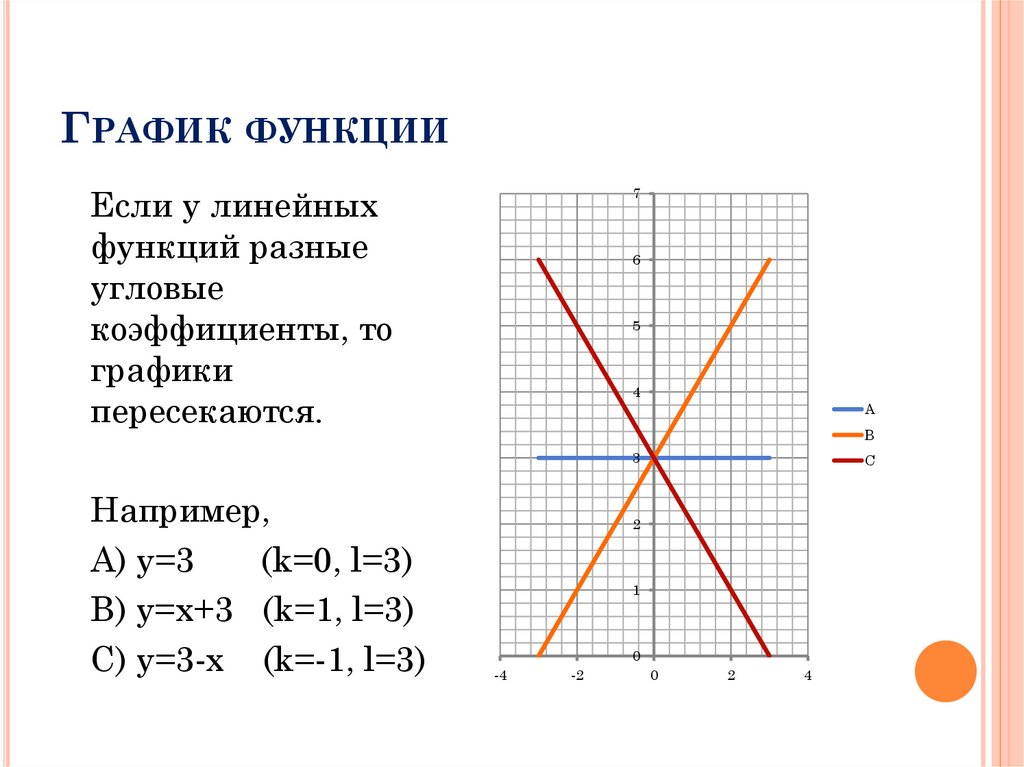
ГРАФИК ФУНКЦИИЕсли у линейных
функций разные
угловые
коэффициенты, то
графики
пересекаются.
7
6
5
4
A
B
3
Например,
А) y=3
(k=0, l=3)
B) y=x+3 (k=1, l=3)
C) y=3-x (k=-1, l=3)
C
2
1
0
-4
-2
0
2
4
6.
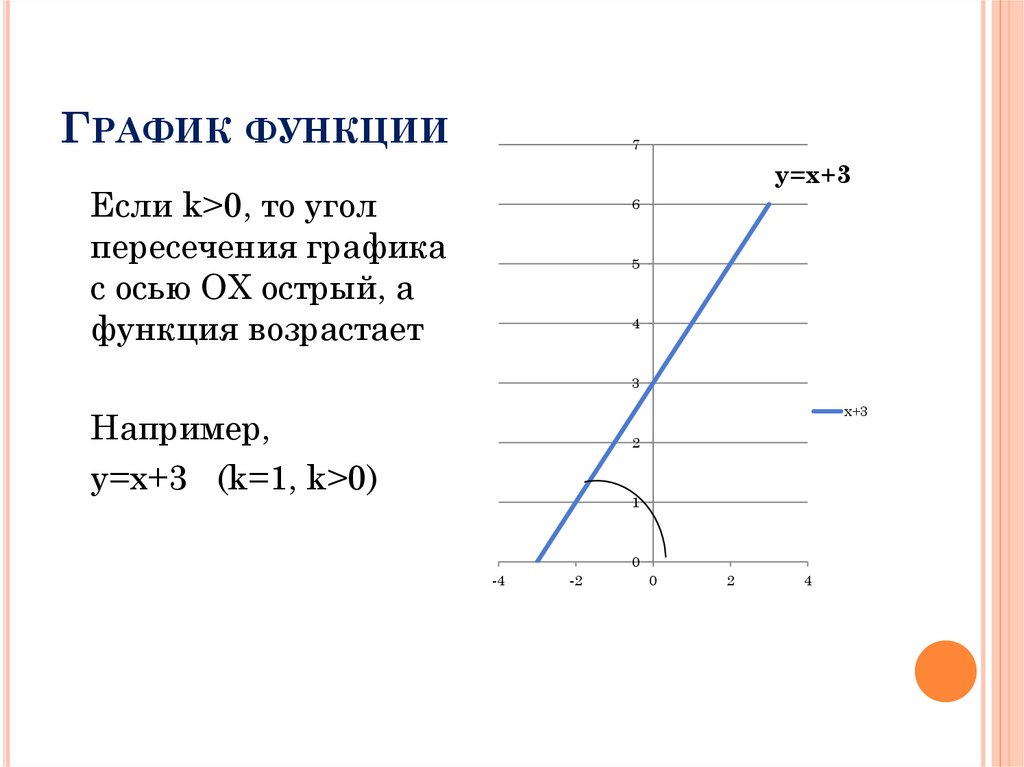
ГРАФИК ФУНКЦИИ7
y=x+3
Если k>0, то угол
пересечения графика
с осью ОХ острый, а
функция возрастает
6
5
4
3
x+3
Например,
у=x+3 (k=1, k>0)
2
1
0
-4
-2
0
2
4
7.
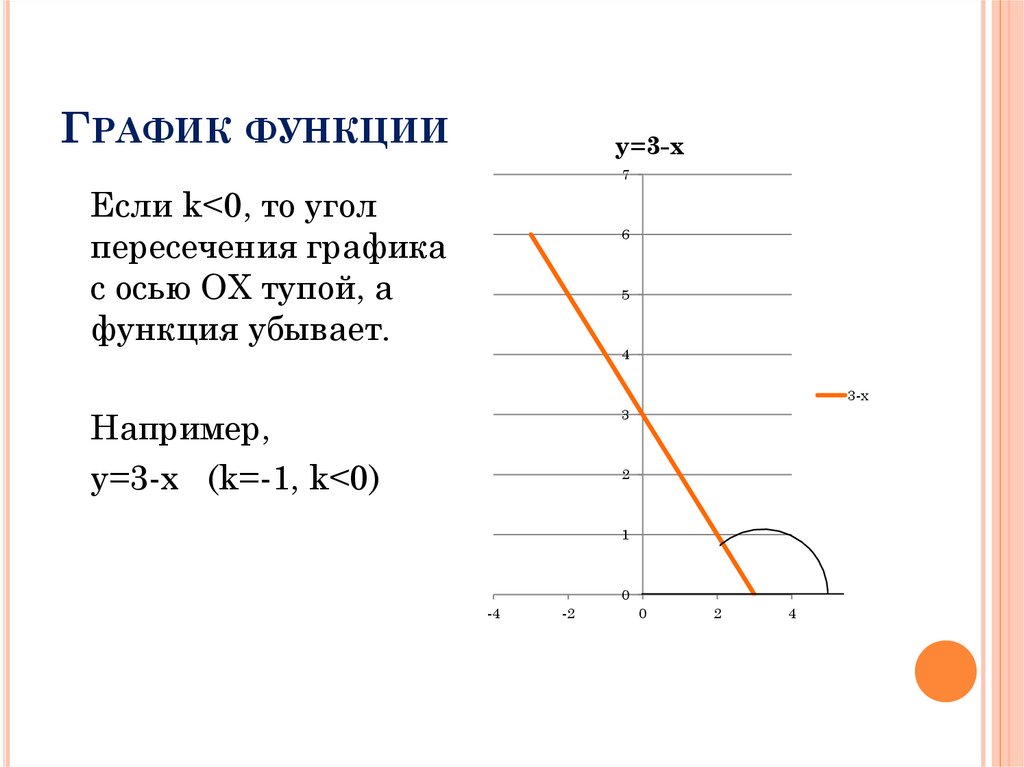
ГРАФИК ФУНКЦИИy=3-x
7
Если k<0, то угол
пересечения графика
с осью ОХ тупой, а
функция убывает.
6
5
4
3-x
3
Например,
y=3-x (k=-1, k<0)
2
1
0
-4
-2
0
2
4
8.
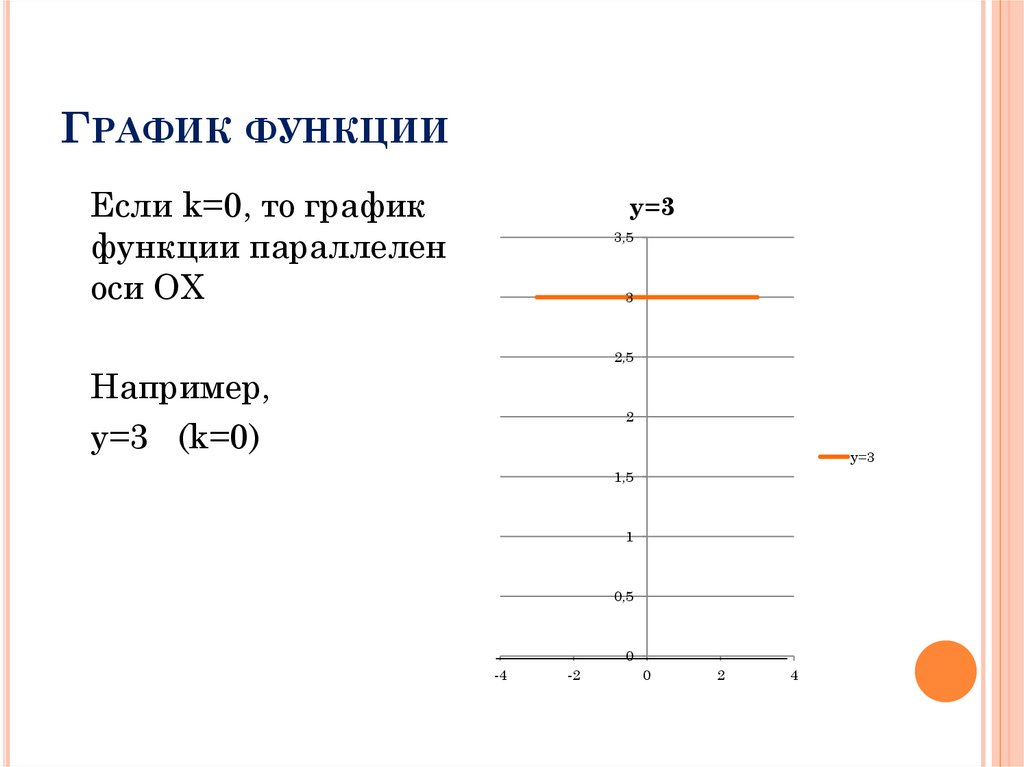
ГРАФИК ФУНКЦИИЕсли k=0, то график
функции параллелен
оси ОХ
y=3
3,5
3
2,5
Например,
y=3 (k=0)
2
y=3
1,5
1
0,5
0
-4
-2
0
2
4
9.
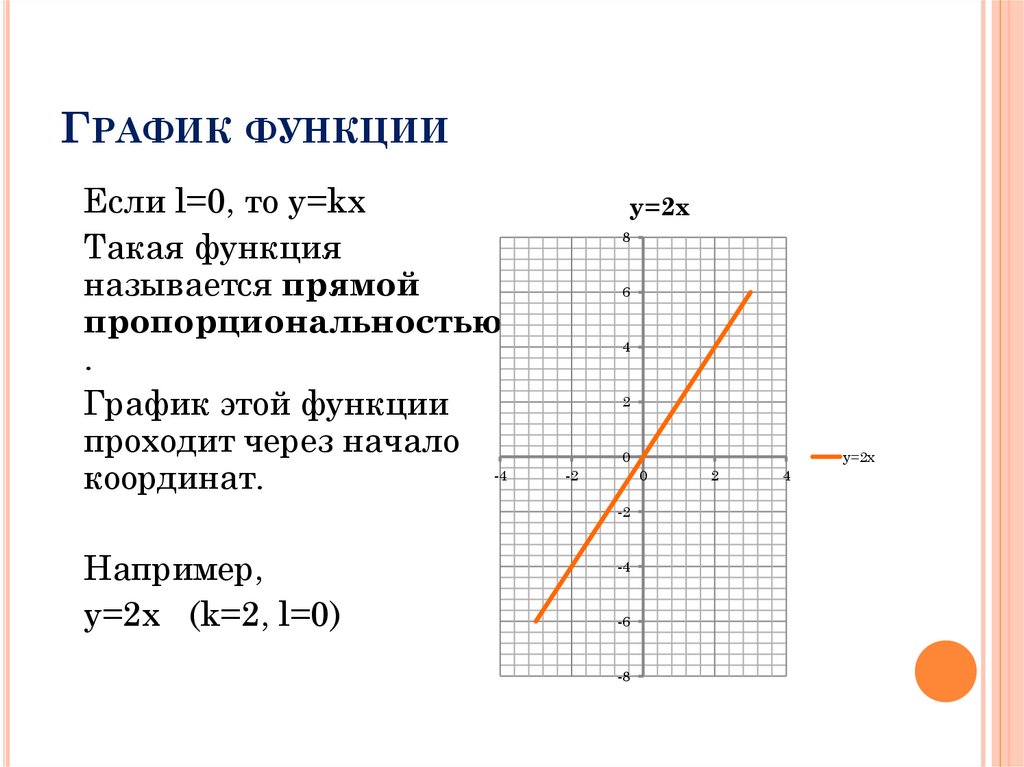
ГРАФИК ФУНКЦИИЕсли l=0, то y=kx
Такая функция
называется прямой
пропорциональностью
.
График этой функции
проходит через начало
-4
координат.
y=2x
8
6
4
2
0
-2
-2
Например,
y=2x (k=2, l=0)
y=2x
0
-4
-6
-8
2
4
10.
СПАСИБОЗА
ВНИМАНИЕ!



 mathematics
mathematics








