Similar presentations:
Логарифмическая функция, её свойства и графики
1.
Потому- то, словно пена,Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
( Б. Слуцкий )
2.
В математике и её приложениях частовстречается логарифмическая функция
y=logax
Где a - заданное число, а>0, а=1
3.
1) Область определения:D(y) = (0; + ∞)
2) Область значений:
E(y) = (− ∞; + ∞)
3) Функция возрастает при а >1.
Функция положительная
4) Функция убывает при 0 < a < 1.
Функция отрицательная
5) Функция y=logax обратная функции
Графики обратных функций симметричны
относительно прямой y=x
D(
E(
)=E(
)=D(
)
)
4.
Если a>1, то функция y=logaxвозрастает.
Принимает положительные значения
при x>1, отрицательные при 0<x<1
Ели 0<a<1, то функция y=logax убывает.
Принимает положительные значения
при 0<x<1, отрицательные при x>1
5.
6.
y log 2 x 4 3-4
0
1
x
7.
yy loglog11 xx 33
22
-3 -2
0 1 2 3
x
8.
22;; 11-4 -3 -2
11;;
x
-1 0 1
y log 1 x 2
2
9.
y log 2 x 10 1
x
y log2 x 1
10.
0 1x
y log2 ( x 2)
11.
y 2 log 2 x 1 -20 1
1
1
0
2
2 ; -2
4
4
2
x









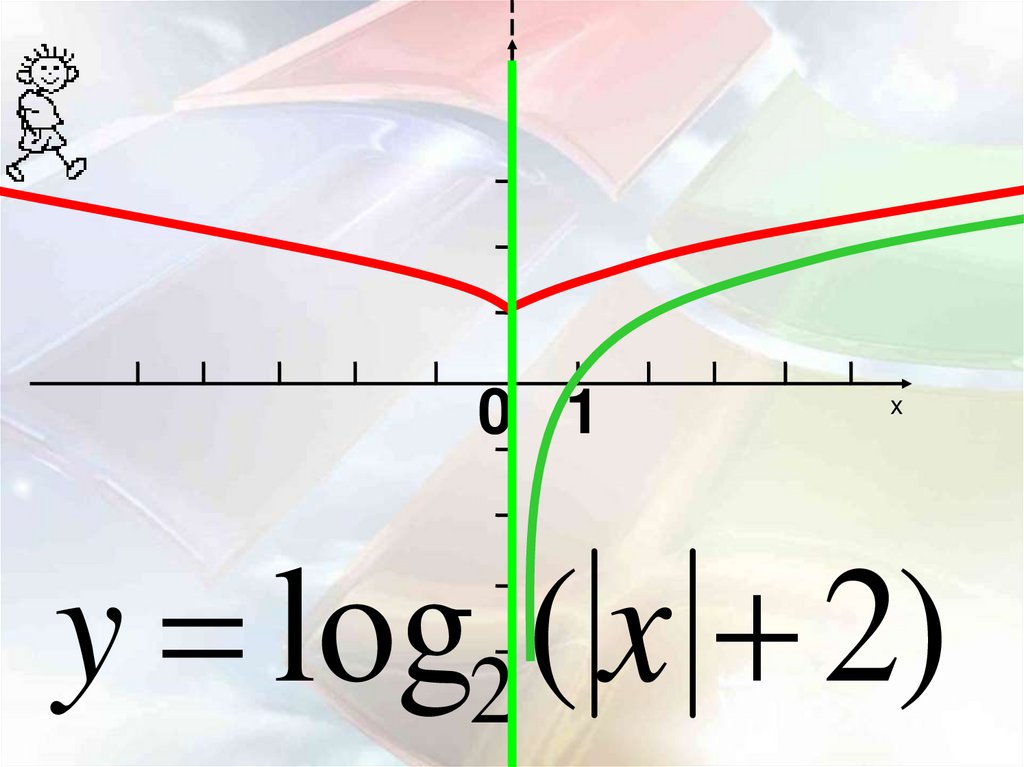

 mathematics
mathematics








