Similar presentations:
Компьютеры и информация
1.
Раздел 1. Компьютеры и информацияТема 1. Принципы работы компьютера
Тема 2. Информация
Тема 3. Представление данных в компьютере
Раздел 2. Основы программирования
Тема 4. Языки программирования
Тема 5. Базовые элементы языка программирования
Тема 6. Концепция типа данных
Раздел 3. Процедурное программирование
Тема 7. Введение в процедурное и структурное программирование
Тема 8. Управляющие инструкции
Тема 9. Базовые структуры данных
Тема 10. Управление памятью
Тема 11. Функции
Тема 12. Асимптотическая оценка сложности алгоритмов
Тема 13. Рекурсия
Тема 14. Связанные динамические структуры данных
Левкович Н.В.
2022/2023
РЕКУРСИЯ
1
2.
Рекурсия* Чтобы понять рекурсию, нужно
сначала понять рекурсию
(народный фольклор)
В математике
Рекурсивная функция - функция, которая определена через
понятие самой этой функции.
Например
factorial(0) = 1
• Факториал
factorial(n) = n * factorial(n-1)
• Ряд чисел Фибоначчи
Левкович Н.В.
2022/2023
F(1) = 0
F(2) = 1
F(n) = F(n-1) + F(n-2)
РЕКУРСИЯ
2
3.
РекурсияВ языках программирования
Рекурсивный алгоритм — это такой способ организации
обработки данных, при котором функция вызывает сама себя
непосредственно, либо с помощью других функций.
Сравните с:
Итерационный алгоритм — это способ организации
обработки данных, при котором определенные действия
повторяются многократно, не приводя при этом к рекурсивным
вызовам функций.
Левкович Н.В.
2022/2023
РЕКУРСИЯ
3
4.
РекурсияРекурсивная функция не может вызывать себя до
бесконечности, поскольку в этом случае она никогда не
завершилась бы.
Следовательно, вторая важная особенность
рекурсивной функции — наличие условия завершения,
позволяющего ей прекратить вызывать себя.
int factorial(int n)
{
if (n == 0)
return 1;
return n * factorial(n - l);
}
Левкович Н.В.
2022/2023
РЕКУРСИЯ
4
5.
Рекурсиярекурсивный алгоритм
итерационный алгоритм
int factorial(int n)
{
if (n == 0)
return 1;
return n * factorial(n - l);
}
int factorial = 1;
for (int i = 2; i <= N; i++)
factorial *= i;
• Любую рекурсивную функцию всегда можно преобразовать в
итерационную, которая выполняет такое же вычисление.
• И наоборот, используя рекурсию, любое вычисление,
предполагающее выполнение циклов, можно реализовать,
не прибегая к циклам.
Левкович Н.В.
2022/2023
РЕКУРСИЯ
5
6.
РекурсияАлгоритм Евклида для нахождения наибольшего общего делителя
для двух целых чисел. Основывается на наблюдении,
что наибольший общий делитель двух целых чисел n и m (m > n),
совпадает с наибольшим общим делителем чисел n и (m % n).
int gcd(int m, int n)
{
cout << "gcd(" << m << ", "
<< n << ")" << endl;
if (n == 0)
return m;
return gcd(n, m % n);
}
Левкович Н.В.
2022/2023
РЕКУРСИЯ
gcd(314159, 271828)
gcd(271828, 42331)
gcd(42331, 17842)
gcd(17842, 6647)
gcd(6647, 4548)
gcd(4548, 2099)
gcd(2099, 350)
gcd(350, 349)
gcd(349, 1)
gcd(1, 0)
6
7.
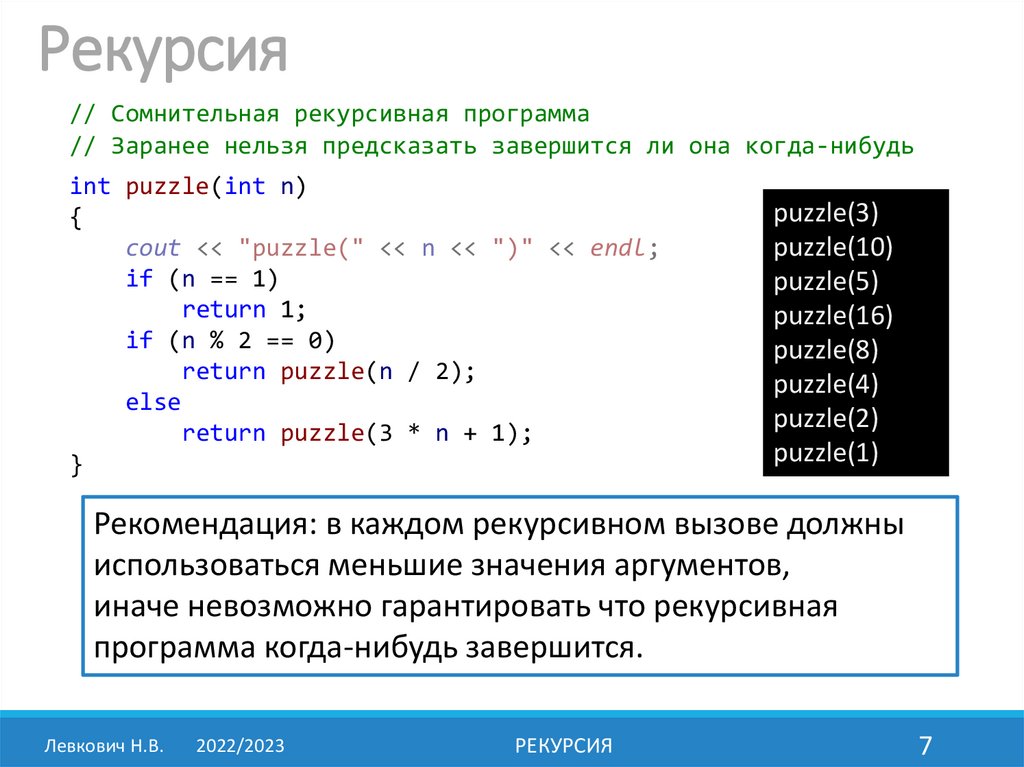
Рекурсия// Сомнительная рекурсивная программа
// Заранее нельзя предсказать завершится ли она когда-нибудь
int puzzle(int n)
{
cout << "puzzle(" << n << ")" << endl;
if (n == 1)
return 1;
if (n % 2 == 0)
return puzzle(n / 2);
else
return puzzle(3 * n + 1);
}
puzzle(3)
puzzle(10)
puzzle(5)
puzzle(16)
puzzle(8)
puzzle(4)
puzzle(2)
puzzle(1)
Рекомендация: в каждом рекурсивном вызове должны
использоваться меньшие значения аргументов,
иначе невозможно гарантировать что рекурсивная
программа когда-нибудь завершится.
Левкович Н.В.
2022/2023
РЕКУРСИЯ
7
8.
РекурсияМаксимальное число рекурсивных вызовов функции без
возвратов, которое происходит во время выполнения
программы, называется глубиной рекурсии.
Число рекурсивных вызовов в каждый конкретный момент
времени, называется текущим уровнем рекурсии.
Левкович Н.В.
2022/2023
РЕКУРСИЯ
8
9.
РекурсияРекурсивные функции могут принимать три формы:
Выполнение действий
Выполнение действий
до рекурсивного вызова после рекурсивного
(с выполнением
вызова
действий
(с выполнением
на рекурсивном
действий
спуске).
на рекурсивном
возврате).
void Rec()
{
… S … ;
if (условие)
Rec();
return;
}
Левкович Н.В.
2022/2023
void Rec()
{
if (условие)
Rec();
… S … ;
return;
}
РЕКУРСИЯ
Выполнение действий
и до и после
рекурсивного вызова
void Rec()
{
… S … ;
if (условие)
Rec();
… S … ;
return;
}
9
10.
РекурсияРекурсивные функции могут принимать три формы:
на рекурсивном спуске
на рекурсивном
возврате
t
0
1
2
3
S
S
S
S
уровень рекурсии
Левкович Н.В.
2022/2023
Выполнение действий
и до и после
рекурсивного вызова
t
0
1
2
3
S
S
S
S
t
0
1
2
3
S
S
S
S
S
S
S
уровень рекурсии
уровень рекурсии
РЕКУРСИЯ
10
11.
РекурсияКакая форма рекурсивной функции использована?
int gcd(int m, int n)
{
cout << "gcd(" << m << ", "
<< n << ")" << endl;
if (n == 0)
return m;
return gcd(n, m % n);
}
* на рекурсивном спуске
Левкович Н.В.
2022/2023
РЕКУРСИЯ
11
12.
Принцип "разделяй и властвуй"Принцип "разделяй и властвуй" предполагает разделение
входного массива данных на две приблизительно равные части
для которых выполняется тот же алгоритм.
Часто его легче реализовать по принципу рекурсии.
В качестве примера рассмотрим задачу поиска
максимального из N элементов, сохраненных в массиве vA[N].
Не рекурсивное решение задачи за один проход массива:
int iMaxVal = vA[0];
for (int i = 1; i < N; i++)
if (vA[i] > iMaxVal)
iMaxval = vA[i];
Левкович Н.В.
2022/2023
РЕКУРСИЯ
12
13.
Принцип "разделяй и властвуй"// поиск максимального элемента в массиве
int FindMax(int vA[], int l, int r)
{
if (l == r)
return vA[l];
int m = (l + r) / 2;
int u = FindMax(vA, l, m);
int v = FindMax(vA, m + 1, r);
return u > v ? u : v;
}
глубина
рекурсии 4
3
2
1
0
Левкович Н.В.
2022/2023
2
3
2
3
3
11
11
8
6
8
6
8
11
4
4
8
10
1
10
1
10
7
5
9
7
5
9
10
11
9
10
11
РЕКУРСИЯ
13
14.
Быстрая сортировкаКолмогоров Андрей
Николаевич
Чарльз Энтони Ричард Хоар
Быстрая сортировка
• реализует принцип "разделяй и властвуй"
• придумана в 1960 г Ч. Э. Р. Хоаром во время обучения в
аспирантуре МГУ по программе обмена студентов
(опубликована в 1962)
Левкович Н.В.
2022/2023
РЕКУРСИЯ
14
15.
Быстрая сортировкаАлгоритм быстрой сортировки:
1) выбрать опорный элемент из массива (любой)
2) разделить массив на две части:
- элементы <= опорного
- элементы >= опорного
3) рекурсивно применить первые два шага к двум
полученным подмассивам.
Рекурсия не применяется к массиву, в котором только
один элемент.
Левкович Н.В.
2022/2023
РЕКУРСИЯ
15
16.
Быстрая сортировкаБыстрая сортировка
опорный элемент
Левкович Н.В.
2022/2023
РЕКУРСИЯ
16
17.
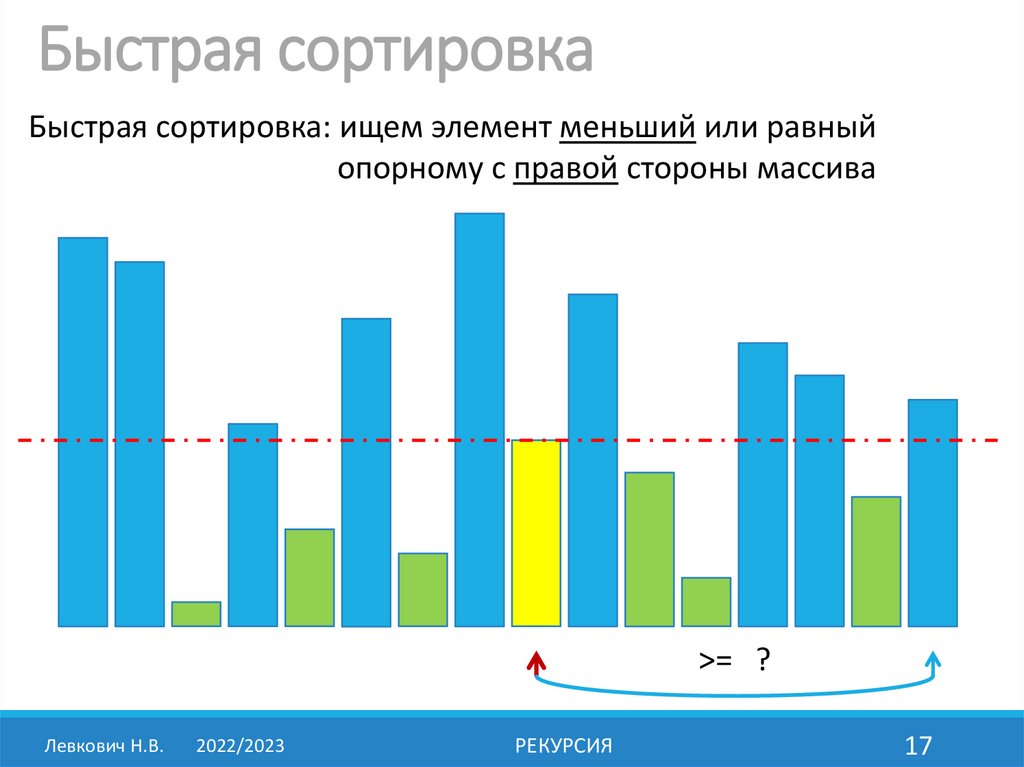
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному c правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
17
18.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
18
19.
Быстрая сортировкаБыстрая сортировка: ищем элемент больший или равный
опорному с левой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
19
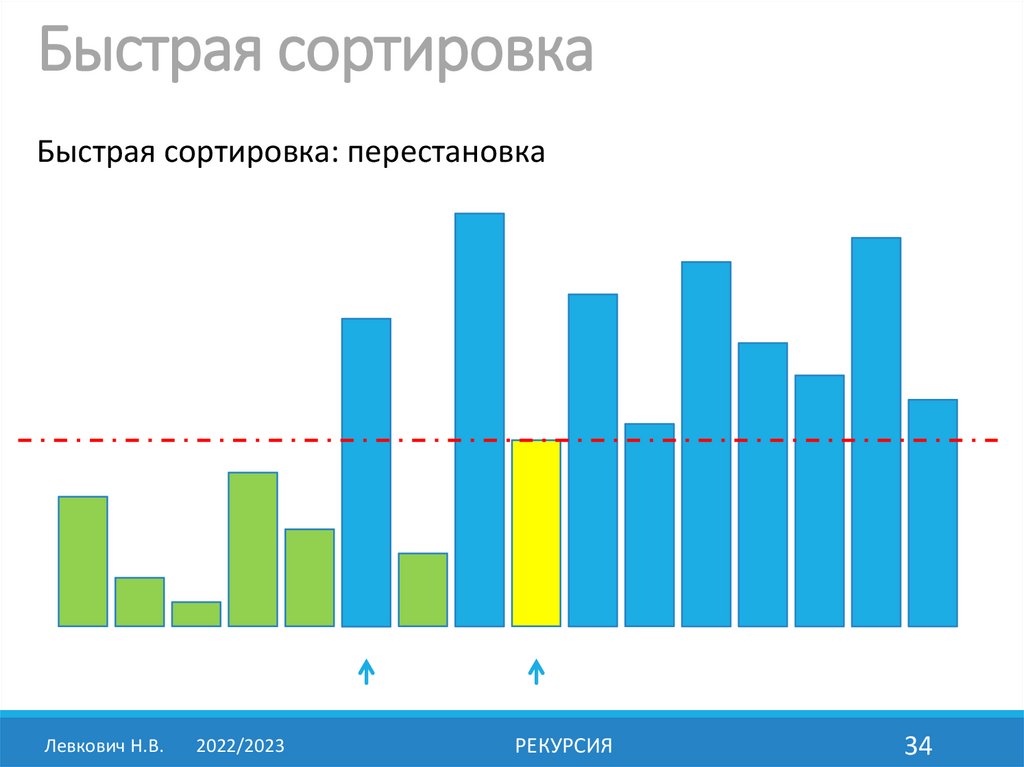
20.
Быстрая сортировкаБыстрая сортировка: перестановка
Левкович Н.В.
2022/2023
РЕКУРСИЯ
20
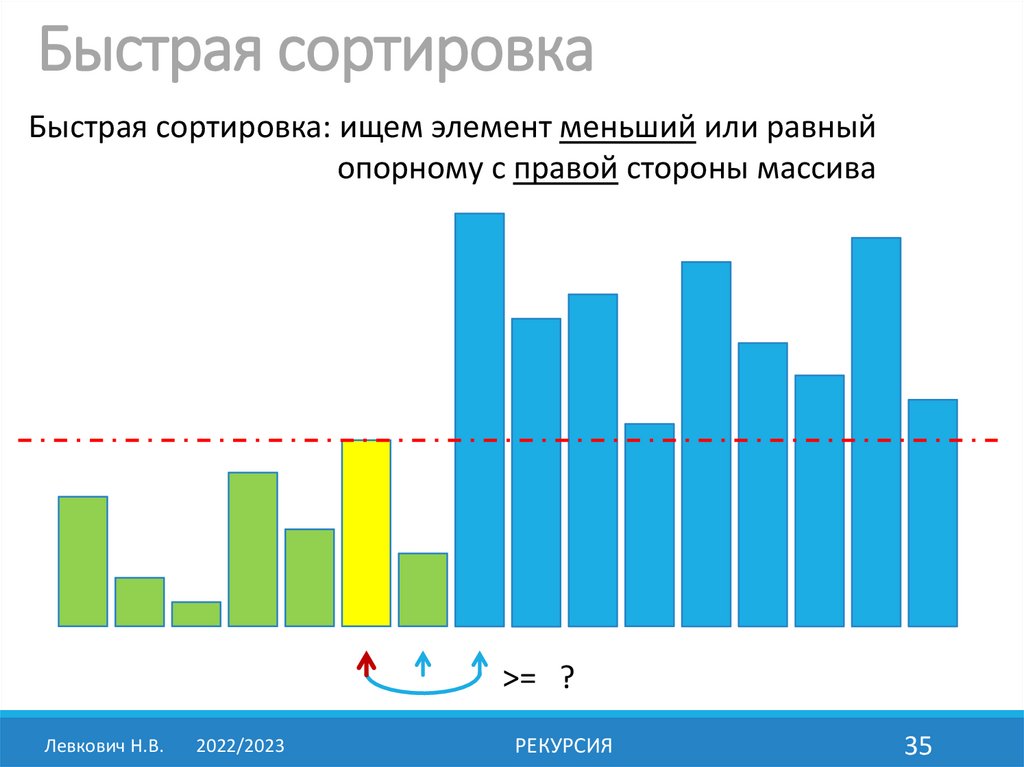
21.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
21
22.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
22
23.
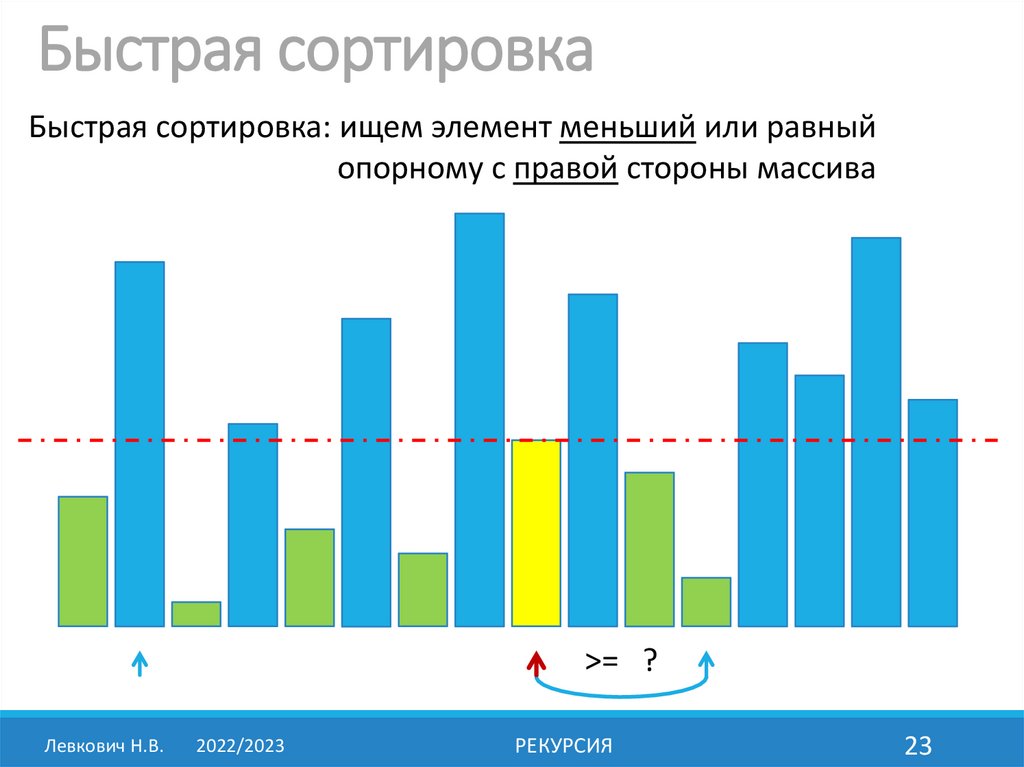
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
23
24.
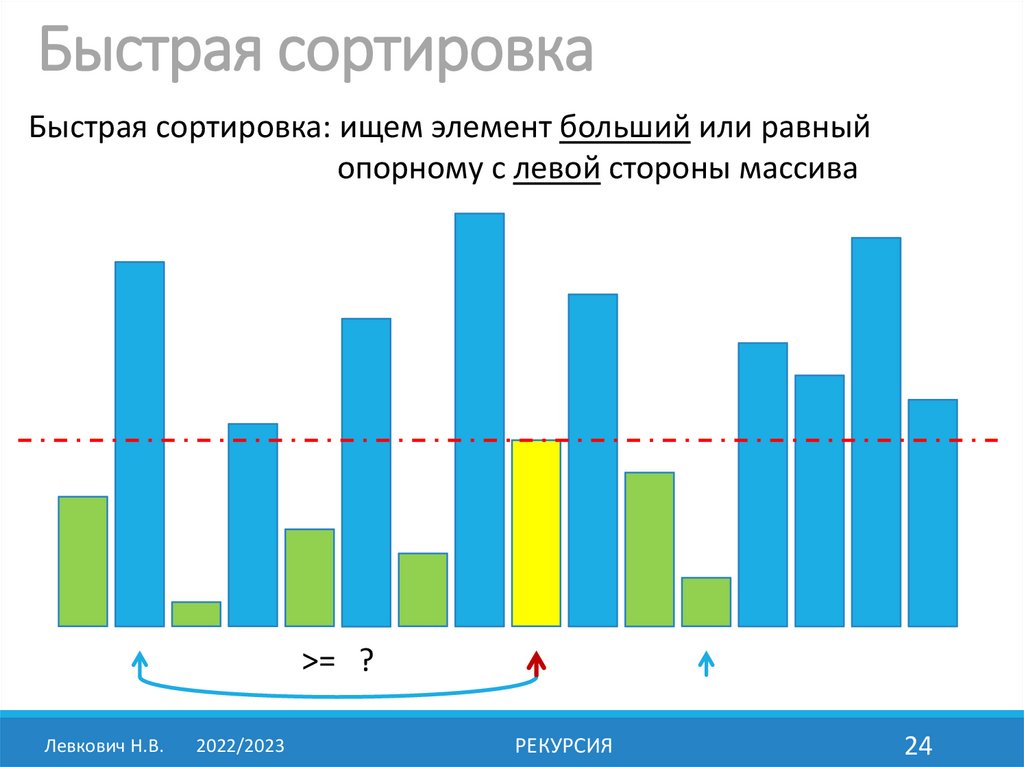
Быстрая сортировкаБыстрая сортировка: ищем элемент больший или равный
опорному с левой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
24
25.
Быстрая сортировкаБыстрая сортировка: перестановка
Левкович Н.В.
2022/2023
РЕКУРСИЯ
25
26.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
26
27.
Быстрая сортировкаБыстрая сортировка: ищем элемент больший или равный
опорному с левой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
27
28.
Быстрая сортировкаБыстрая сортировка: ищем элемент больший или равный
опорному с левой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
28
29.
Быстрая сортировкаБыстрая сортировка: перестановка
Левкович Н.В.
2022/2023
РЕКУРСИЯ
29
30.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
30
31.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
31
32.
Быстрая сортировкаБыстрая сортировка: ищем элемент больший или равный
опорному с левой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
32
33.
Быстрая сортировкаБыстрая сортировка: ищем элемент больший или равный
опорному с левой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
33
34.
Быстрая сортировкаБыстрая сортировка: перестановка
Левкович Н.В.
2022/2023
РЕКУРСИЯ
34
35.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
>= ?
Левкович Н.В.
2022/2023
РЕКУРСИЯ
35
36.
Быстрая сортировкаБыстрая сортировка: ищем элемент меньший или равный
опорному с правой стороны массива
указатели встретились
конец первой итерации
Левкович Н.В.
2022/2023
РЕКУРСИЯ
36
37.
Быстрая сортировка• итерация заканчивается когда указатели в правой части массива
и левой сходятся на одном элементе
• за один этап все элементы были разделены на две группы,
при этом было произведено N операций сравнения
• больше перемещений между этими группами не требуется
• нужно только отсортировать элементы внутри каждой из групп:
вызвать рекурсивно тот же алгоритм для них
• опорный элемент попадает в одну из групп и необязательно
будет на границе разделения групп
• группы не будут одинаковыми по размеру
• для полной сортировки массива размера N понадобится в
лучшем случае ~log2(N) таких этапов, итого сложность NlogN
• даже если делление массива на каждой итерации будет в
соотношении 1 к 3, то это даст N log3/4(N), а это тот же NlogN
Левкович Н.В.
2022/2023
РЕКУРСИЯ
37
38.
Быстрая сортировкаvoid Qsort(int vA[], int l, int r)
{
int iReper = vA[(l + r) / 2];
int i = l;
int j = r;
while (i <= j)
{
while (vA[i] < iReper)
i++;
while (vA[j] > iReper)
j--;
if (i <= j)
{
swap(vA[i], vA[j]);
i++;
j--;
}
}
if (l < j)
Qsort(vA, l, j);
if (i < r)
Qsort(vA, i, r);
return;
}
Левкович Н.В.
2022/2023
В данной реализации
алгоритма
правая граница массива
включается, то есть для
сортировки массива
vA[N] нужно вызывать
Qsort(vA, 0, N - 1);
РЕКУРСИЯ
38
39.
Быстрая сортировка2
6
4
9
1
3
5
7
8
1
6
4
9
2
3
5
7
8
1
2
4
9
6
3
5
7
8
1
2
3
9
6
4
5
7
8
1
2
3
4
6
9
5
7
8
1
2
3
4
5
9
6
7
8
1
2
3
4
5
6
9
7
8
1
2
3
4
5
6
7
9
8
1
2
3
4
5
6
7
8
9
Левкович Н.В.
2022/2023
РЕКУРСИЯ
В очень редких
"неудачных" случаях
быстрая сортировка может
обладать сложностью N2.
На практике такое
совпадение может
случиться, если
какой-нибудь хакер
подсунет вашей
программе специально
подобранный массив
данных.
39
40.
Быстрая сортировка• Сложность быстрой сортировки:
o минимум: N·log(N)
o в среднем: N·log(N)
o максимум: N2
• Это самая быстрая сортировка (в среднем) на случайных данных.
Существуют сортировки с той же асимптотической сложностью,
но при этом с ощутимо большей константой.
• Работает медленнее сортировки вставками на уже
упорядоченных массивах (или близких к таковым).
• Если неудачно выбран опорный элемент, то сложность этой
сортировки возрастает до N2 по времени и до N по занимаемой
памяти в стеке, что может приводить к ошибке переполнения
стека (STACK_OVERFLOW)
Левкович Н.В.
2022/2023
РЕКУРСИЯ
40
41.
Быстрая сортировкаЯвляется ли быстрая сортировка устойчивой?
(Быстрая сортировка является неустойчивой)
исходный массив
\/ \/ \/
Иванов
Ковалёв
Козлов
Новиков
Иванов
Ковалёв
Козлов
Новиков
Иванов
Ковалёв
Козлов
Левкович Н.В.
Александр
Алексей
Артем
Владислав
Даниил
Дмитрий
Иван
Илья
Максим
Михаил
Никита
2022/2023
отсортированный
устойчивым методом
\/ \/ \/
Иванов
Иванов
Иванов
Ковалёв
Ковалёв
Ковалёв
Козлов
Козлов
Козлов
Новиков
Новиков
отсортированный
неустойчивым методом
\/ \/ \/
Александр
Даниил
Максим
Алексей
Дмитрий
Михаил
Артем
Иван
Никита
Владислав
Илья
РЕКУРСИЯ
Иванов
Иванов
Иванов
Ковалёв
Ковалёв
Ковалёв
Козлов
Козлов
Козлов
Новиков
Новиков
Даниил
Максим
Александр
Дмитрий
Алексей
Михаил
Никита
Иван
Артем
Илья
Владислав
41
42.
Шаблоны функцийvoid swap(int& a, int& b)
{
int tmp = a;
a = b;
b = tmp;
}
template <typename T>
void swap(T& a, T& b)
{
T tmp = a;
a = b;
b = tmp;
}
void swap(float& a, float& b)
{
float tmp = a;
a = b;
b = tmp;
}
int main()
{
int x = 15,
y = 2;
swap(IN OUT x, IN OUT y);
cout << x << " " << y << endl;
return 0;
}
Левкович Н.В.
2022/2023
РЕКУРСИЯ
Эта функция
обменивает значения
передаваемых ей
через ссылки
переменных
любого типа
2 15
42
43.
Шаблоны функцийtemplate <typename T>
void swap(T& a, T& b)
{
T tmp = a;
a = b;
b = tmp;
}
int main()
{
int x = 15,
y = 2;
swap<int>(x, y);
swap(x, y);
return 0;
}
Левкович Н.В.
2022/2023
Явное указание типа
шаблонного параметра
Если тип шаблонного
параметра не указан
явно при вызове, то он
будет определён
автоматически по
типам аргументов,
передаваемых в
функцию
РЕКУРСИЯ
43
44.
Шаблоны функцийtemplate <typename T>
bool Greater(T a, T b)
{
return a > b;
}
bool Greater(char* a, char* b)
{
return strcmp(a, b) > 0;
}
bool Greater(const char* a, const char* b)
{
return strcmp(a, b) > 0;
}
Шаблонная функция может быть перегружена не шаблонной
функцией. В этом случае не шаблонная функция будет иметь
приоритет.
Это удобно использовать при реализации алгоритма
сортировки через шаблонную функцию.
Шаблонная функция может быть перегружена другим
шаблоном с таким же именем, но с другим набором
параметров.
Левкович Н.В.
2022/2023
РЕКУРСИЯ
44
45.
Теорема о сложности сортировкиТеорема: не существует алгоритма сортировки
массива из N элементов,
основанного на попарном сравнении элементов,
выполняющегося для всех возможных входных
данных с асимптотикой лучше чем N·log(N)
1. Определение сортировки:
a1, a2, … an ak1, ak2, … akn
f(ak1) f(ak2) f(ak3) … f(akn)
2. Сколько всего вариантов
перестановок элементов массива A[N]?
N!
3. На каждом шаге используем операцию сравнения двух
элементов 'больше', результат bool
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
45
46.
Теорема о сложности сортировки2. Сколько всего вариантов
перестановок элементов массива A[N]?
N!
3. На каждом шаге используем операцию сравнения двух
элементов 'больше', результат bool.
После каждого сравнения часть первоначально возможных
перестановок будет удовлетворять результату операции
сравнения, а часть не будет. Перестановки неудовлетворяющие
результату сравнения отбрасываем.
(a1, a2, a3) (a1, a3, a2) (a2, a1, a3) (a2, a3, a1 ) (a3, a1, a2) (a3, a2, a1)
a1 > a2 =>
(a1, a2, a3) (a1, a3, a2) (a2, a1, a3) (a2, a3, a1 ) (a3, a1, a2) (a3, a2, a1)
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
46
47.
Теорема о сложности сортировки2. Сколько всего вариантов
перестановок элементов массива A[N]?
N!
3. На каждом шаге используем операцию сравнения двух
элементов 'больше', результат bool.
После каждого сравнения часть первоначально возможных
перестановок будет удовлетворять результату операции
сравнения, а часть не будет. Перестановки неудовлетворяющие
результату сравнения отбрасываем.
Составляя алгоритм, мы не можем влиять на результат операции
сравнения (он может получиться любой), но можем подбирать
лучший вопрос – выбрать сравниваемые элементы.
Каким образом выбрать сравниваемые элементы, чтобы
количество возможных перестановок уменьшалось быстрее
всего?
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
47
48.
Теорема о сложности сортировки2. Сколько всего вариантов
перестановок элементов массива A[N]?
N!
3. На каждом шаге используем операцию сравнения двух
элементов 'больше', результат bool.
После каждого сравнения часть первоначально возможных
перестановок будет удовлетворять результату операции
сравнения, а часть не будет. Перестановки неудовлетворяющие
результату сравнения отбрасываем.
Быстрее всего количество вариантов будет сокращаться,
если обе группы будут одинакового размера
(группа перестановок удовлетворяющих результату сравнения
двух выбранных элементов '>' и удовлетворяющих условию '<=')
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
48
49.
Теорема о сложности сортировки2. Сколько всего вариантов
перестановок элементов массива A[N]?
N!
3. На каждом шаге используем операцию сравнения двух
элементов 'больше', результат bool.
После каждого сравнения часть первоначально возможных
перестановок будет удовлетворять результату операции
сравнения, а часть не будет. Перестановки неудовлетворяющие
результату сравнения отбрасываем.
Итак на каждом шаге количество вариантов перестановок
будет в лучшем случае уменьшаться в два раза.
Какое количество шагов нам понадобится чтобы N! вариантов
уменьшилось до 1?
log2(N!)
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
49
50.
Теорема о сложности сортировки2. Сколько всего вариантов
перестановок элементов массива A[N]?
N!
3. На каждом шаге используем операцию сравнения двух
элементов 'больше', результат bool.
После каждого сравнения часть первоначально возможных
перестановок будет удовлетворять результату операции
сравнения, а часть не будет. Перестановки неудовлетворяющие
результату сравнения отбрасываем.
4. Минимальное количество шагов
(а значит и операций сравнения) равно
log2(N!) log2(NN) = N·log2(N)
ЧТД
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
50
51.
Сложность алгоритмов сортировкиАлгоритм
Вспомогательные
данные
В худшем
В худшем
Временная сложность
Лучшее
В среднем
Быстрая сортировка
N log(N)
N log(N)
N2
N
Сортировка слиянием
N log(N)
N log(N)
N log(N)
N
Пирамидальная сортировка
N log(N)
N log(N)
N log(N)
1
Пузырьковая сортировка
N
N2
N2
1
Сортировка вставками
N
N2
N2
1
Сортировка выбором
N2
N2
N2
1
Блочная сортировка
N+K
N+K
N2
NK
Поразрядная сортировка
NK
NK
NK
N+K
хорошо
приемлимо
плохо
https://habr.com/post/188010/
Левкович Н.В.
2022/2023
ТЕОРЕМА О СЛОЖНОСТИ СОРТИРОВКИ
51
52.
Вопросы2. Рекурсия. Рекурсивные определения. Сравнение рекурсивной
и итерационной реализаций алгоритмов.
Глубина и текущий уровень рекурсии. Конечность рекурсии.
3. Структура рекурсивных процедур:
вычисления на рекурсивном спуске и рекурсивном возврате.
4. Рекурсивный алгоритм быстрой сортировки.
Оценка сложности быстрой сортировки.
5. Повторное использование исходного кода.
Шаблоны функций.
6. Теорема о предельной сложности сортировки, основанной на
попарном сравнении элементов.
Левкович Н.В.
2022/2023
52














































 programming
programming informatics
informatics








