Сетевые педагогические сообщества как форма самообразования и повышение квалификации учителя

1. Сетевые педагогические сообщества как форма самообразования и повышение квалификации учителя.

Подготовила- учитель математики
Горбачёва С.В.

2.

Сегодня от учителя требуется
«готовность достойно
встречать каждую
профессиональную
ситуацию, быть готовым к
переподготовке в быстро
меняющихся условиях».

3.

Самообразование как
постоянная
деятельность учителя
включает:

4.

• 1. научно-
исследовательскую
работу по определенной
проблеме;

5.

• 2. посещение библиотек,
изучение научнометодической и учебной
литературы;

6.

• 3. участие в педсоветах,
научно-методических
объединениях;

7.

• 4. посещение уроков
своих коллег, обмен
мнениями по вопросам
организации занятий,
содержания обучения,
методов преподавания;

8.

• 5. теоретическую
разработку и практическую
апробацию разных форм
уроков, внеклассных
мероприятий и учебных
материалов.

9.

10.

11. Ресурсы сайта

Цифровые образовательные ресурсы
Элементы Единой коллекции ЦОР
Планы-конспекты уроков
Мастер-классы
Дистанционное обучение
Все материалы сайта
Комментарии к материалам сайта
Документы МОН

12. Сетевое педагогическое сообщество МСО г.Ярославля

Сообщество создано с
целью развития
структуры
единого
информационнообразовательного
пространства
МСО г. Ярославля.

13.

Фестиваль педагогических идей «Открой себя»
1. Подборка и классификация задач с
практическим содержанием. Горбачёва С.В.
МОУ СОШ №40.
2. Сценарий открытого урока по математике в
6 классе по теме «Действия с рациональными
числами. Горбачёва С.В. МОУ СОШ №40.
3. несколько предложений по изучению темы
«Модуль». Горбачёва С.В. МОУ СОШ №40.
4. Задача- основное средство в обучении
математике. Маркелова Л.И. МОУ СОШ №40

14. Общероссийский проект Школа цифрового века Проект разработан в соответствии с программой модернизации системы общего

1
signIn
Общероссийский проект Школа цифрового века
Проект разработан в соответствии с программой модернизации
системы общего образования России
Вход в
личный
кабинет
Пользовате
ль
Пароль
Регистрация нового пользователя
Забыли?
Войти
(«Открытый урок», «Портфолио»,
Педагогический университет)
https://my.1september.ru/

15.

• Задачи:
-обобщение, распространение и
обсуждение методических аспектов
проектно-исследовательской
деятельности;
-обсуждение педагогических
технологий, адекватных проектноисследовательской деятельности и
распространение опыта педагогов;
-популяризация опыта работы
школьных научных обществ учащихся,
системы работы с одаренными
учащимися;

16.

• -предоставление всем желающим
(учителям и учащимся) возможности
разработки и осуществление различных
совместных исследований и сетевых
проектов;
-возможность реализовать свой
творческий и интеллектуальный
потенциал при разработке выбранной
темы исследования;
-информирование о региональных
конкурсных программах;

17.

• -содействие развитию и
совершенствованию умений и
навыков учащихся в проведении
исследовательских работ;
-совершенствование навыков работы с
телекоммуникационными
технологиями;
-возможность для учителей и учащихся
накопления материала для личного
портфолио.

18.

Сетевые профессиональные
сообщества учителей
Владимирова Людмила Павловна, н.с.
лаборатории ДО ИСМО РАО

19.

• Сетевые сообщества или объединения
учителей – это новая форма организации
профессиональной деятельности в сети.
Участие в профессиональных сетевых
объединениях позволяет учителям,
живущим в разных уголках одной страны и
за рубежом общаться друг с другом, решать
профессиональные вопросы, реализовать
себя и повышать свой профессиональный
уровень.

20.

• Рассмотрим некоторые сетевые сообщества, а
именно, виртуальные объединения учителей в
нашей стране и за рубежом.
• Это - Содружество методических объединений
(СОМ) http://center.fio.ru/som/,
• Всероссийский @августовский ИнтернетПедсовет http://pedsovet.alledu.ru,
• «Интернет - государство учителей» (ИнтерГУру
www.intergu.ru),
• некоторые региональные объединения
учителей России и Еропейская Школьная Сеть
www.eun.org.

21.

Сеть творческих учителей создана
для педагогов, которые интересуются
возможностями
обучения
с
улучшения
помощью
качества
применения
информационных и коммуникационных
технологий (ИКТ).
На этом портале вы найдете разнообразные
материалы
и
ресурсы,
касающиеся
использования ИКТ в учебном процессе, а
также сможете пообщаться со своими
коллегами.

22.

• Интегрированный урок (алгебра + технология) в 7-м классе <566545>
Горбачева С.В., Беляев И.Е.
• В работе представлен конспект интегрированного урока алгебры и
технического труда. Урок является примером реализации
межпредметных связей как внутри одного предмета, так и смежных
предметов, информационно насыщен, направлен на развитие
учащихся, способных анализировать, сопоставлять факты и применять
теоретические знания на практике.
• Интегрированный урок (алгебра + физика) "Первообразная и
интеграл в задачах" <565996> Молоткова Л.Ф., Мудревская Д.И.
• Цель данного урока – показать применение первообразной,
интеграла при расчетах площади фигур, объема тел, а также при
решении задач в различных разделах физики. Урок показывает, что
математика тесно связана с профессиональной деятельностью
человека.

23.

24.

ДодекаэдрДодекаэдр
Додекаэдр
(от греческого dodeka – двенадцать и hedra – грань) – это правильный
многогранник, составленный из двенадцати
пятиугольников.
Сумма длин всех
ребер
Площадь
поверхности
тетраэдра
равносторонних
30a
S 3a 2 5(5 2 5)
Объем
a3
V (15 7 5 )
4
Радиус описанной
сферы
a
R (1 5 ) 3
4
Радиус вписанной
сферы
r
a
22
10
4
5
Плоскостей симметрии 9 и проходят они либо
через противоположные ребра
(таковых плоскостей 6), либо через середины
противоположных ребер (таких - 3). Додекаэдр
имеет 15 плоскостей симметрии. Любая из
плоскостей симметрии проходит в каждой грани
через вершину и середину противоположного
ребра.

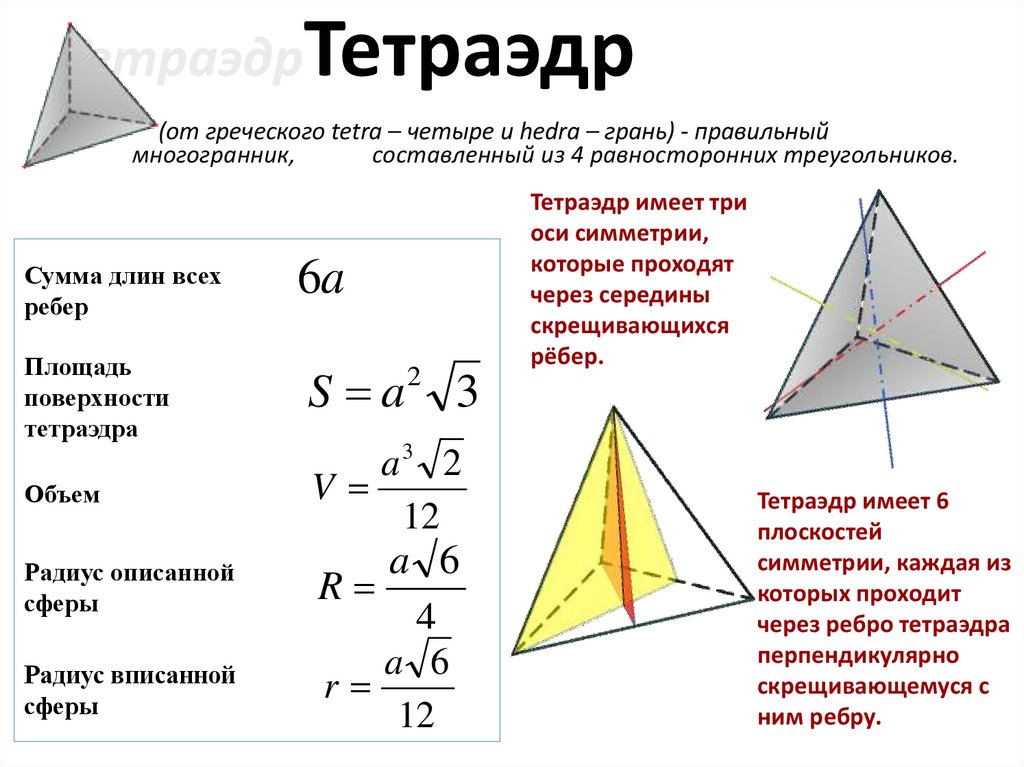
25. ТетраэдрТетраэдр  (от греческого tetra – четыре и hedra – грань) - правильный многогранник, составленный из 4 равносторонних

ТетраэдрТетраэдр
(от греческого tetra – четыре и hedra – грань) - правильный
многогранник,
составленный из 4 равносторонних треугольников.
Сумма длин всех
ребер
Тетраэдр имеет три
оси симметрии,
которые проходят
через середины
скрещивающихся
рёбер.
6a
Площадь
поверхности
тетраэдра
S a
Объем
a3 2
V
12
Радиус описанной
сферы
a 6
R
4
Радиус вписанной
сферы
a 6
r
12
2
3
Тетраэдр имеет 6
плоскостей
симметрии, каждая из
которых проходит
через ребро тетраэдра
перпендикулярно
скрещивающемуся с
ним ребру.

26. Платоновы тела

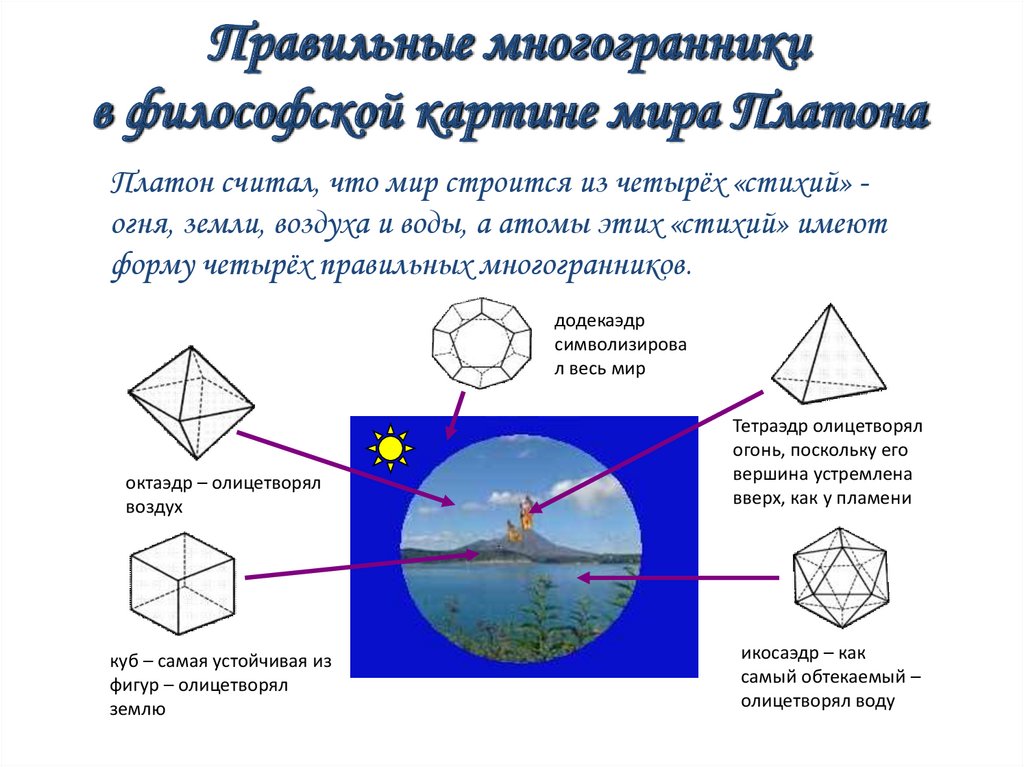
Гексаэдр Тетраэдр Октаэдр Икосаэдр Додекаэдр

27. Правильные многогранники в философской картине мира Платона

Платон считал, что мир строится из четырёх «стихий» огня, земли, воздуха и воды, а атомы этих «стихий» имеют
форму четырёх правильных многогранников.
додекаэдр
символизирова
л весь мир
октаэдр – олицетворял
воздух
Тетраэдр олицетворял
огонь, поскольку его
вершина устремлена
вверх, как у пламени
куб – самая устойчивая из
фигур – олицетворял
землю
икосаэдр – как
самый обтекаемый –
олицетворял воду

28.

29.

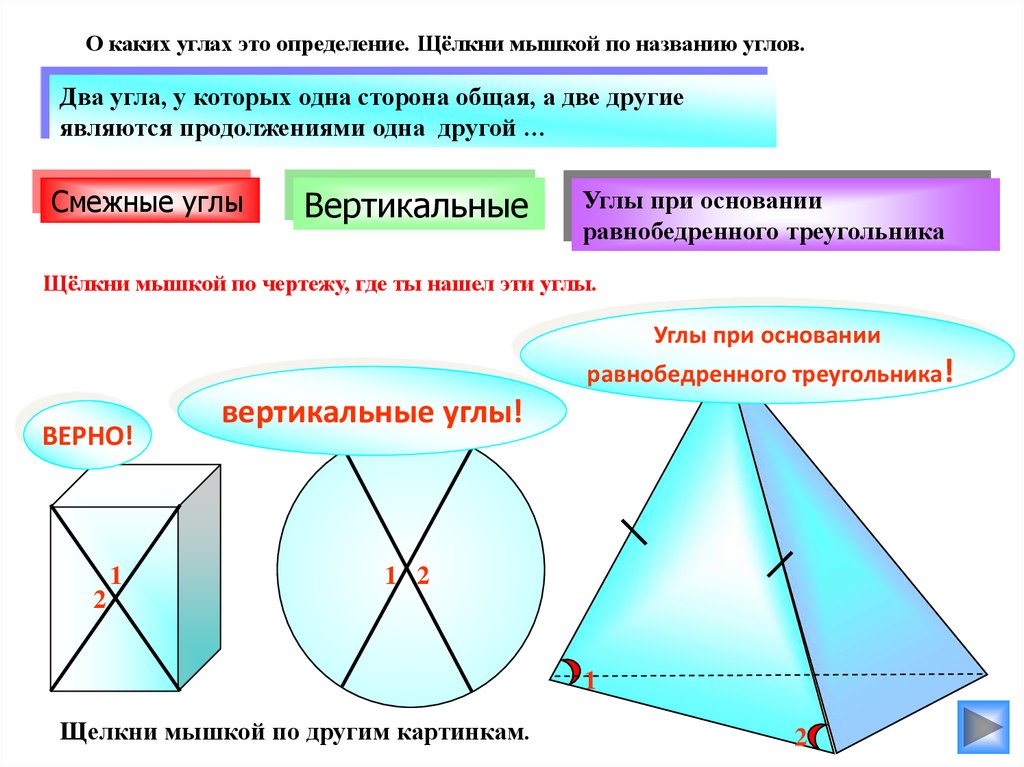
О каких углах это определение. Щёлкни мышкой по названию углов.
Два угла, у которых одна сторона общая, а две другие
являются продолжениями одна другой …
Смежные углы
Вертикальные
Углы при основании
равнобедренного треугольника
Щёлкни мышкой по чертежу, где ты нашел эти углы.
Углы при основании
равнобедренного треугольника!
ВЕРНО!
1
вертикальные углы!
1 2
2
1
Щелкни мышкой по другим картинкам.
2

30.

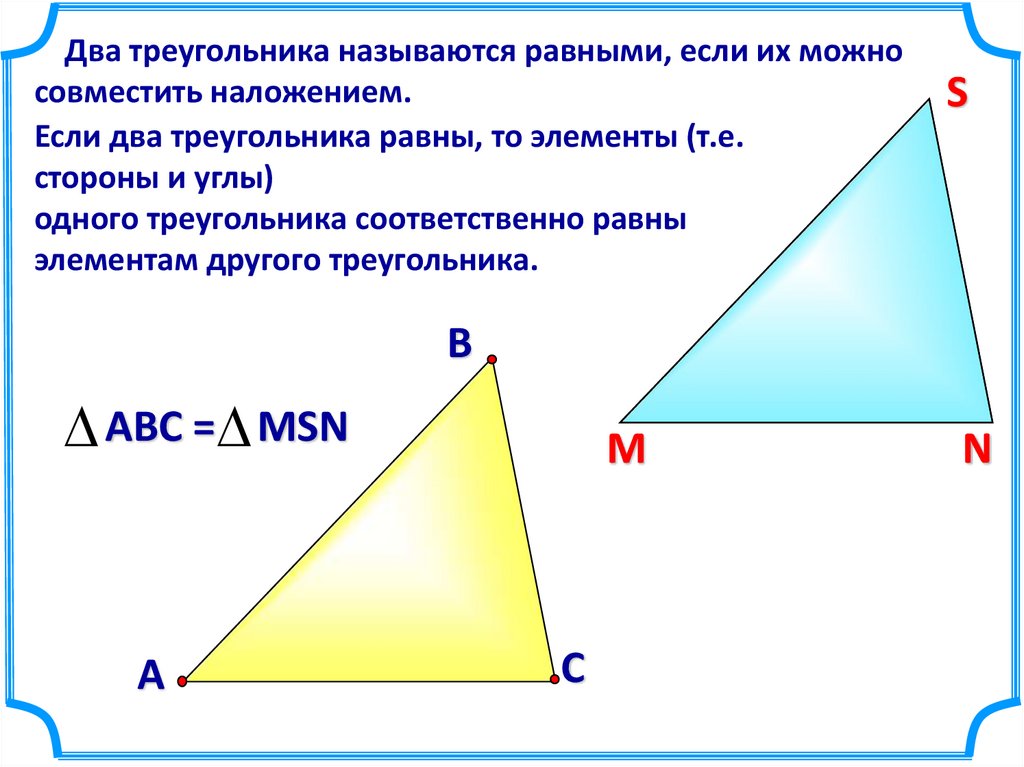
Два треугольника называются равными, если их можно
совместить наложением.
Если два треугольника равны, то элементы (т.е.
стороны и углы)
одного треугольника соответственно равны
элементам другого треугольника.
S
В
АВС = MSN
А
М
С
N

31.

Определение.
Две прямые на плоскости
называются параллельными,
если они не пересекаются.