Similar presentations:
Решение уравнений
1. Решение уравнений
Учитель математики высшейквалификационной категории
гимназии № 36 г. Казани
Игнатьева В. А.
2.
Уравнением называют равенство,содержащее букву, значение
которой надо найти.
Значение буквы, при котором из
уравнения получается верное
числовое равенство, называется
корнем уравнения.
3.
Решить уравнение – значит найтивсе его корни или убедиться, что
оно не имеет корней.
4.
Уравнение, которое можно привести квиду ax = b, где a ≠ 0, называют
линейным уравнением с одним
неизвестным.
5.
Корни уравнения не изменяются,если обе части уравнения
умножить или разделить на одно и
то же число, не равное нулю.
Корни уравнения не изменяются,
если какое-нибудь слагаемое
перенести из одной части
уравнения в другую, изменив при
этом его знак.
6.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
7.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
Решение.
2,1x ̶ 3,5 = 1,4 x;
8.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
Решение.
2,1x ̶ 3,5 = 1,4 x;
2,1x ̶ 1,4 x = 3,5;
9.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
Решение.
2,1x ̶ 3,5 = 1,4 x;
2,1x ̶ 1,4 x = 3,5;
0,7x = 3,5;
10.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
Решение.
2,1x ̶ 3,5 = 1,4 x;
2,1x ̶ 1,4 x = 3,5;
0,7x = 3,5;
x = 3,5:0,7;
11.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
Решение.
2,1x ̶ 3,5 = 1,4 x;
2,1x ̶ 1,4 x = 3,5;
0,7x = 3,5;
x = 3,5:0,7;
x = 5.
12.
Решите уравнение:2,1x ̶ 3,5 = 1,4 x.
Решение.
2,1x ̶ 3,5 = 1,4 x;
2,1x ̶ 1,4 x = 3,5;
0,7x = 3,5;
x = 3,5:0,7;
x = 5.
Ответ: 5.
13.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
14.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
Решение.
8 ̶ 3,8x = 0,8 ̶ 0,2x;
15.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
Решение.
8 ̶ 3,8x = 0,8 ̶ 0,2x;
̶ 3,8x + 0,2x = 0,8 ̶ 8;
16.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
Решение.
8 ̶ 3,8x = 0,8 ̶ 0,2x;
̶ 3,8x + 0,2x = 0,8 ̶ 8;
̶ 3,6x = ̶ 7,2;
17.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
Решение.
8 ̶ 3,8x = 0,8 ̶ 0,2x;
̶ 3,8x + 0,2x = 0,8 ̶ 8;
̶ 3,6x = ̶ 7,2;
x = ̶ 7,2:( ̶ 3,6);
18.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
Решение.
8 ̶ 3,8x = 0,8 ̶ 0,2x;
̶ 3,8x + 0,2x = 0,8 ̶ 8;
̶ 3,6x = ̶ 7,2;
x = ̶ 7,2:( ̶ 3,6);
x = 2.
19.
Решите уравнение:2·(4 ̶ 1,9 x) = 0,8 ̶ 0,2x.
Решение.
8 ̶ 3,8x = 0,8 ̶ 0,2x;
̶ 3,8x + 0,2x = 0,8 ̶ 8;
̶ 3,6x = ̶ 7,2;
x = ̶ 7,2:( ̶ 3,6);
x = 2.
Ответ: 2.
20.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке первоначально?
21.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке первоначально?
22.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке
первоначально?
Было
Стало (книг)
(книг)
Верхняя
полка
Нижняя
23.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке
первоначально?
Было
Стало (книг)
(книг)
Верхняя
полка
Нижняя
x
24.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке
первоначально?
Было
Стало (книг)
Верхняя
полка
Нижняя
(книг)
3x
x
25.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке
первоначально?
Было
Стало (книг)
Верхняя
полка
Нижняя
(книг)
3x
x
3x ̶ 15
26.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке
первоначально?
Было
Стало (книг)
Верхняя
полка
Нижняя
(книг)
3x
3x ̶ 15
x
x + 11
27.
Задача. На верхней полке в 3раза больше книг, чем на
нижней. После того, как с
верхней полки сняли 15 книг, а
на нижнюю добавили 11 книг,
книг на обеих полках стало
поровну. Сколько книг было на
каждой полке
первоначально?
Было
Стало (книг)
Верхняя
полка
Нижняя
(книг)
3x ?
3x ̶ 15
x
x + 11
?
поровну
28.
3x ̶ 15 = x + 11;29.
3x ̶ 15 = x + 11;3x ̶ x =11 + 15;
30.
3x ̶ 15 = x + 11;3x ̶ x =11 + 15;
2x = 26;
31.
3x ̶ 15 = x + 11;3x ̶ x =11 + 15;
2x = 26;
x = 26:2;
32.
3x ̶ 15 = x + 11;3x ̶ x =11 + 15;
2x = 26;
x = 26:2;
x = 13 (книг) было на нижней
полке;
33.
3x ̶ 15 = x + 11;3x ̶ x =11 + 15;
2x = 26;
x = 26:2;
x = 13 (книг) было на нижней
полке;
3·13 = 39 (книг) было на верхней
полке.
34.
3x ̶ 15 = x + 11;3x ̶ x =11 + 15;
2x = 26;
x = 26:2;
x = 13 (книг) было на нижней
полке;
3·13 = 39 (книг) было на верхней
полке.
Ответ: 39 книг было на верхней
полке, 13 книг было на нижней
35.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
36.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Скорость Время
(км/ч)
(ч)
Автобус
Автомобил
ь
Путь
(км)
37.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Скорость Время
(км/ч)
(ч)
Автобус
Автомобил x ?
ь
Путь
(км)
38.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Автобус
Скорость Время
(км/ч)
(ч)
x ̶ 20
Автомобил x ?
ь
Путь
(км)
39.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Автобус
Скорость Время
(км/ч)
(ч)
x ̶ 20
4
Автомобил x ?
ь
Путь
(км)
40.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Автобус
Скорость Время
(км/ч)
(ч)
x ̶ 20
4
Автомобил x ?
ь
3
Путь
(км)
41.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Автобус
Скорость Время
Путь
(км/ч)
(ч)
(км)
x ̶ 20
4
4(x ̶ 20)
Автомобил x ?
ь
3
42.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Автобус
Скорость Время
Путь
(км/ч)
(ч)
(км)
x ̶ 20
4
4(x ̶ 20)
Автомобил x ?
ь
3
3x
43.
Задача Путь из города в село автобуспроехал за 4 часа. Скорость легкового
автомобиля на 20 км/ч больше, и он
проехал этот же путь за 3 часа. Найдите
скорость легкового автомобиля.
Автобус
Скорость Время
Путь
(км/ч)
(ч)
(км)
x ̶ 20
4
4(x ̶ 20)
Автомобил x ?
ь
3
3x
равно
44.
4(x ̶ 20) = 3x;45.
4(x ̶ 20) = 3x;4x ̶ 80 = 3x;
46.
4(x ̶ 20) = 3x;4x ̶ 80 = 3x;
4x ̶ 3x = 80 ;
47.
4(x ̶ 20) = 3x;4x ̶ 80 = 3x;
4x ̶ 3x = 80 ;
x = 80 (км/ч) скорость легкового
автомобиля.
48.
4(x ̶ 20) = 3x;4x ̶ 80 = 3x;
4x ̶ 3x = 80 ;
x = 80 (км/ч) скорость легкового
автомобиля.
Ответ: 80 км/ч скорость легкового
автомобиля.
49.
Тренажер по математикеЗадание 56. Уравнения с десятичными числами.
Режим: контроль. Количество задач: 10. Система
оценивания: 5 баллов




























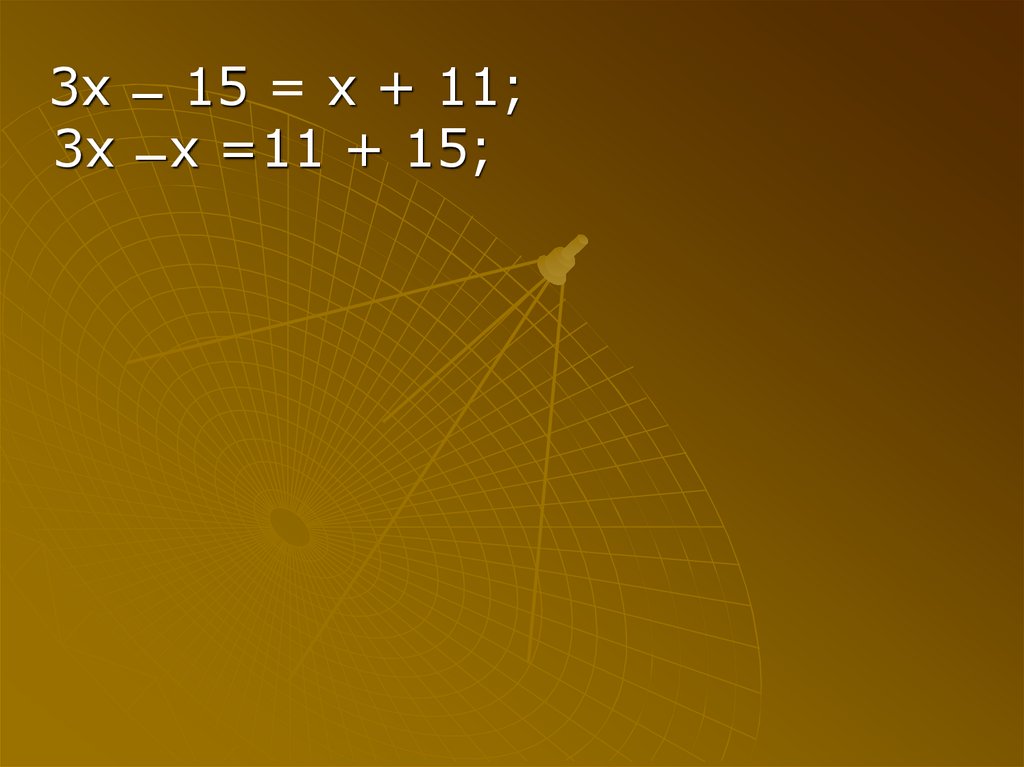
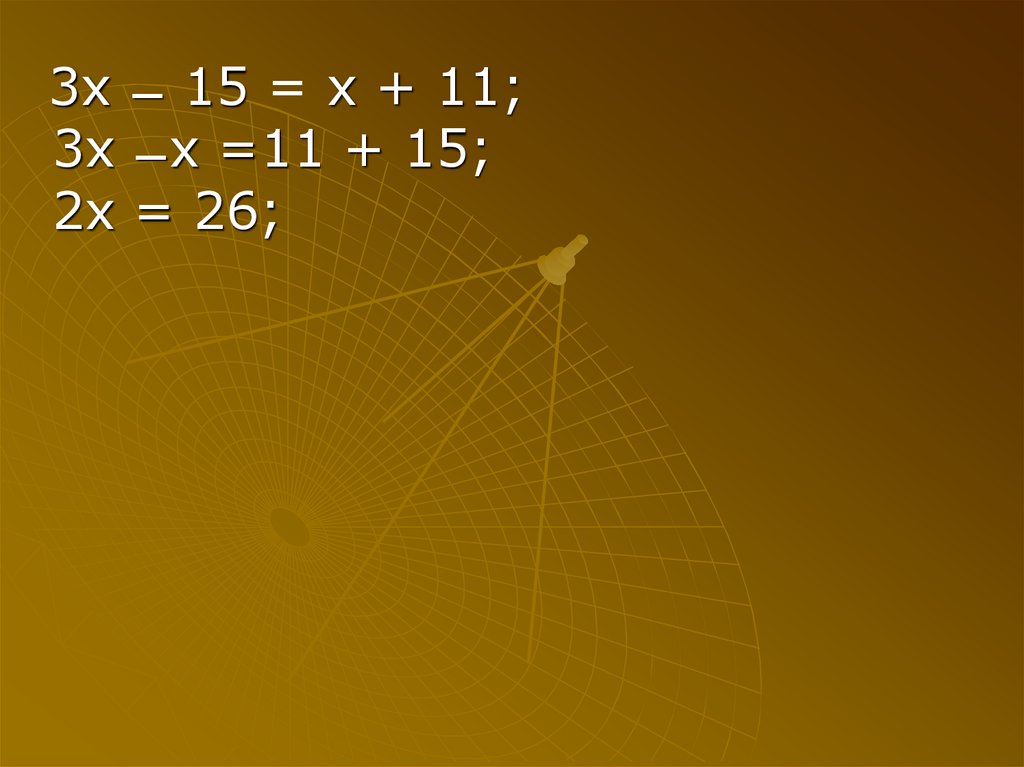
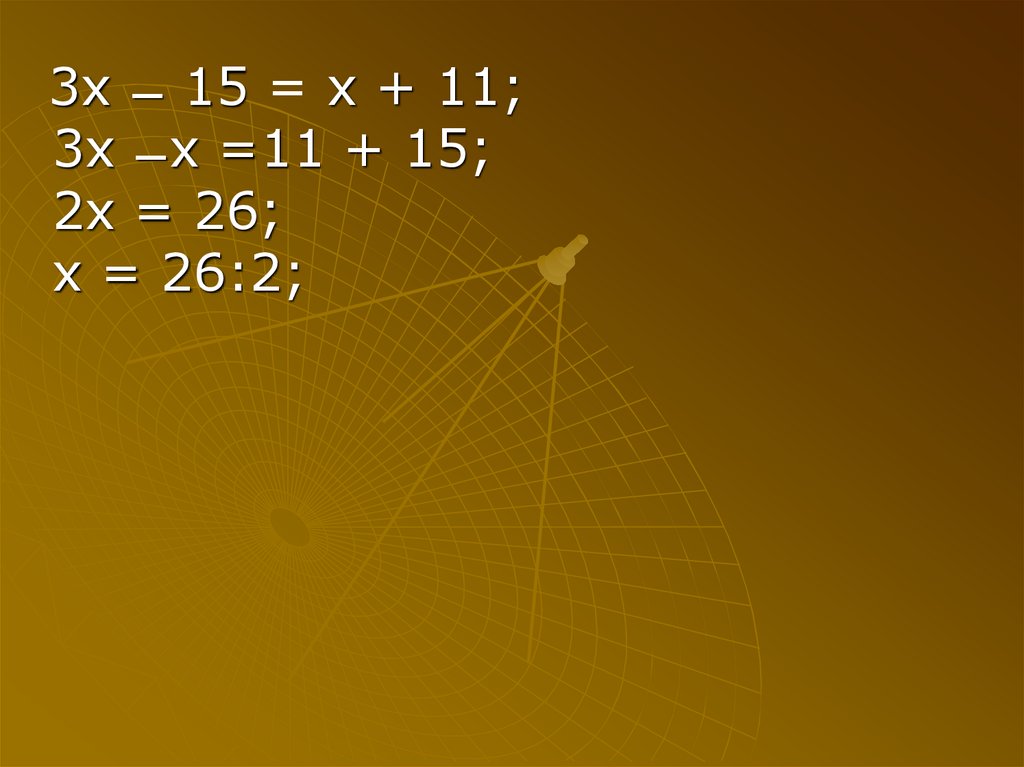












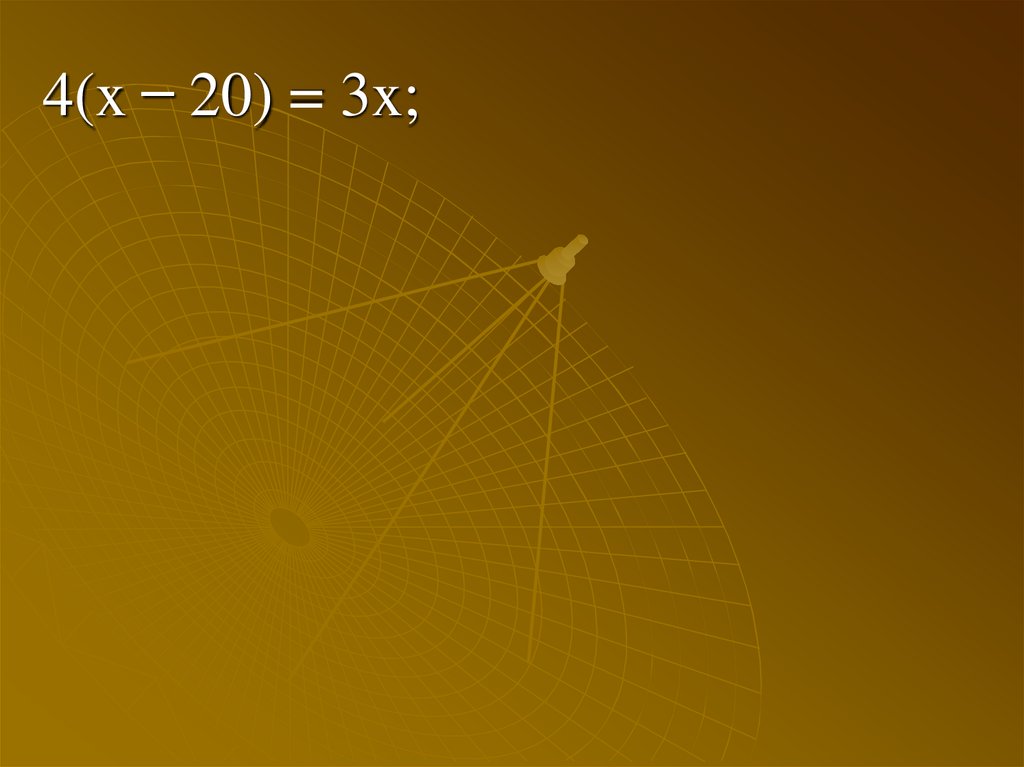
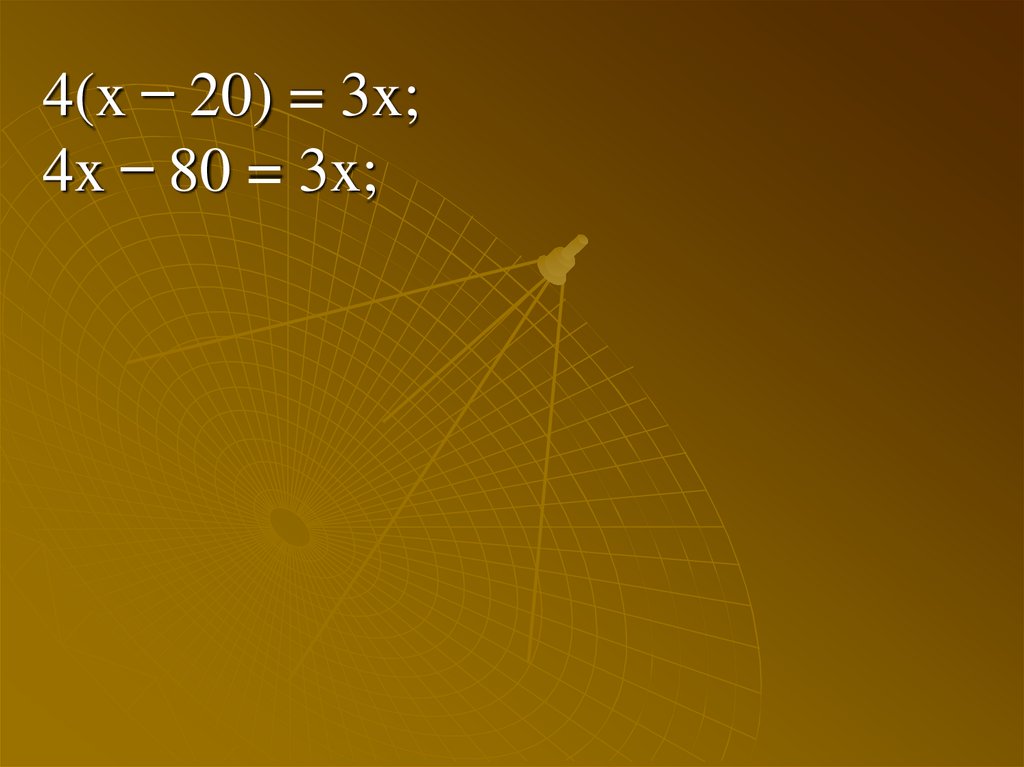
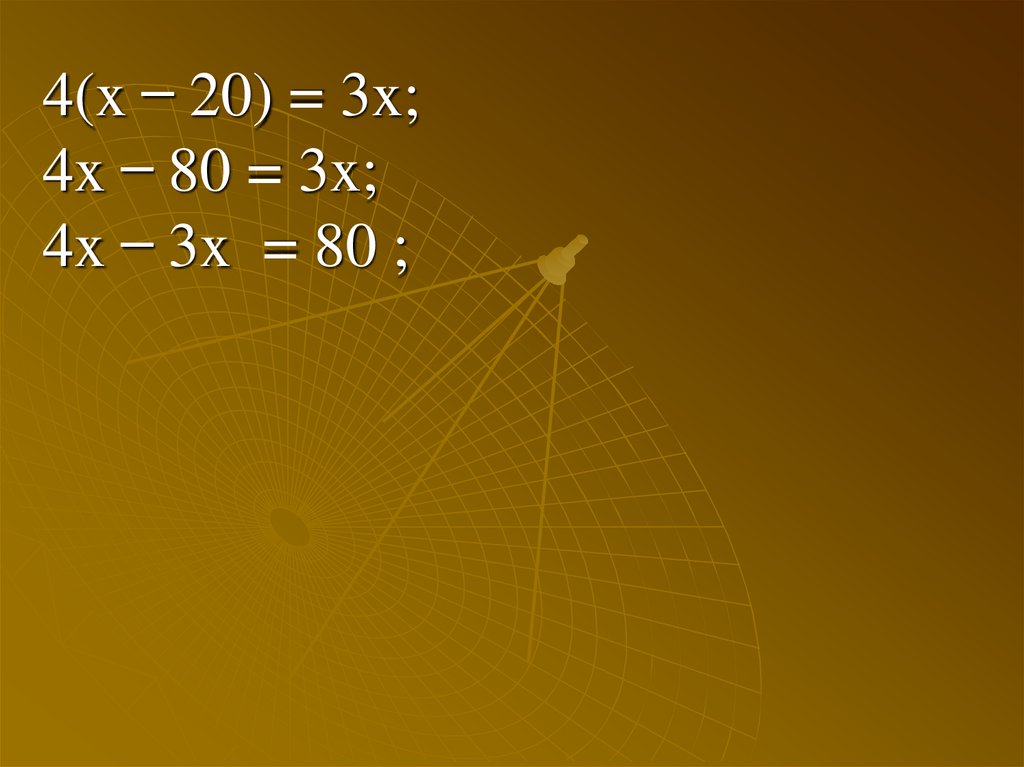



 mathematics
mathematics








