Similar presentations:
Свойства биссектрисы угла. Урок математики. 5 класс
1.
Урок математики5 класс
Сибгатуллина Милеуша Дамировна –
учитель математики
МБОУ «БОЛЬШЕКАЙБИЦКАЯ СОШ»
2.
3.
Петр I Великий(Петр Алексеевич Романов) (1672 - 1725)
4.
5.
6.
По чертежам Петра I. Под Петербургомстроят копию корабля «Полтава»
7.
ПРАВИЛА:Слушать.
Слышать друг друга.
Дополнять. Исправлять,
помогать.
8.
ПовторениеРасстояние между двумя точками.
Расстояние от точки до прямой.
Какие прямые называются перпендикулярными?
Что такое биссектриса
Как можно построить биссектрису?
9.
Тема урока:СВОЙСТВА
БИССЕКТРИСЫ УГЛА.
10.
Цель урока:выявить свойство
биссектрисы угла.
11.
12.
13.
А?
О
В
?
С
ОА = ОС
14.
Учебное исследование №21. Начертите тупой(прямой, острый)угол
2. Проведите его биссектрису.
3. Отметьте на ней произвольную точку О.
4. Опустите из неё перпендикуляр на стороны
угла.
5. Измерьте длины перпендикуляров и
сравните их.
6. Будут ли точки этой биссектрисы
равноудалены от сторон угла?
15.
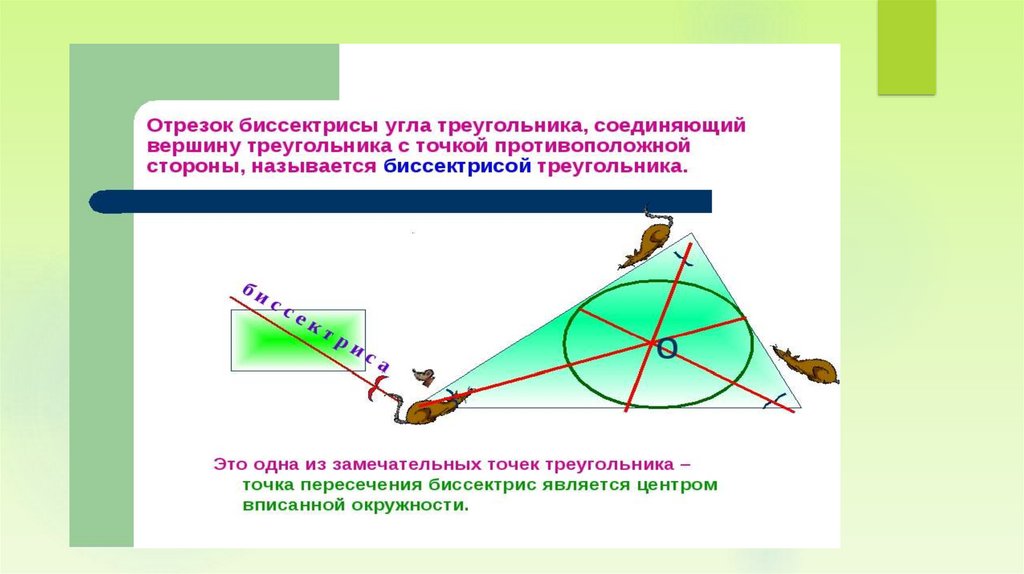
ВЫВОД:Точки биссектрисы любого
угла равноудалены от сторон
угла. Это и есть свойство
биссектрисы угла.
16.
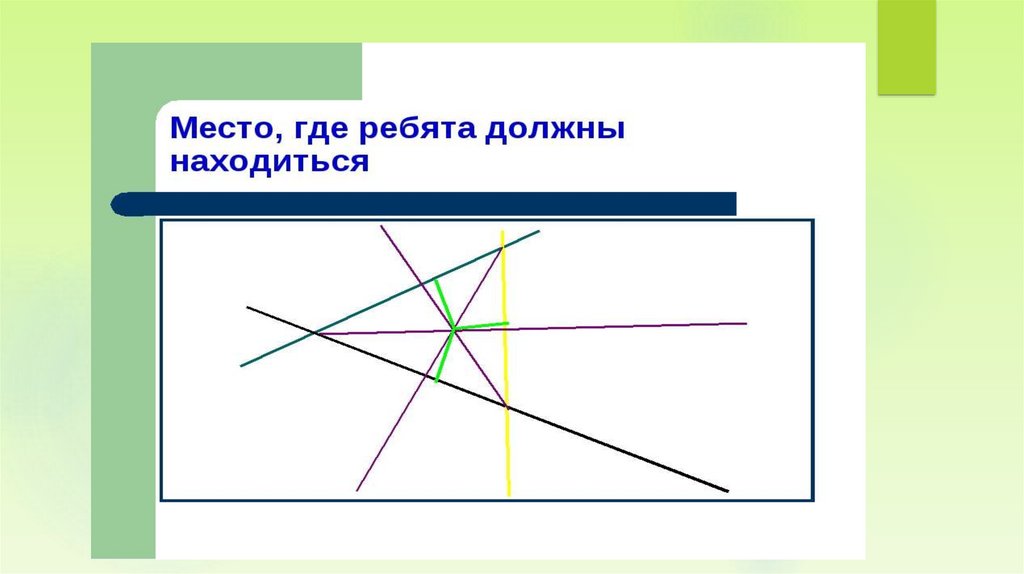
Учебное исследование №3Маша и Саша решили путешествовать
автостопом. В один из дней своего путешествия
они оказались в треугольнике, образованным
тремя дорогами, и тут у них разгорелся спор – в
какую сторону и по какой дороге ехать. В конце
концов они решили поехать по той дороге, по
которой пойдет первая же машина. Покажите, где
они должны стоять, чтобы находиться на
одинаковом расстоянии от каждой из трех дорог.
Ответ обоснуйте.
17.
Учебное исследование №3.Где же должны стоять ребята?
Точка пересечения биссектрис - это
и есть место, где должны стоять
ребята, чтобы находиться на
одинаковом расстоянии от каждой
трёх дорог.
Почему?
18.
19.
20.
Собери бабочкуБабочки-красота и чудо природы.
Берегите природу!
21.
Итог урока:Какую задачу мы решали
сегодня на уроке?
Каким свойством обладает
биссектриса?
Все точки биссектрисы
любого угла равноудалены от
его сторон.
22.
Домашнее задание :1. Начертите разные по виду треугольники и
проверьте в них свойство биссектрисы угла.
2. Начертите три тупых угла так, чтобы два из
них не имели общих точек, а стороны третьего
пересекали бы лишь одну сторону каждого из
первых двух углов. (Математические олимпиады)



















 mathematics
mathematics








